目次
・藤崎モデルのパラメータ逆推定をやってみる②
・実装
- ①前処理:補間
- ①前処理:マイクロプロソディの除去
- ②ハイパスフィルタで分解
- ③フレーズコマンドの初期推定
- ④アクセントコマンドの初期推定
- ⑤最適化
・結果
・終わり
藤崎モデルのパラメータ逆推定をやってみる②
今回は前回やった
「【基本周波数で遊ぶ】藤崎モデルのパラメータ逆推定をやってみる」の別論文についてを扱う。
\begin{align}
\log F_0[t] &= F_b + F_p[t] + F_a[t] \\
&= F_b + \sum_i Ap_iG_p(t - T_{0i}) + \sum_j Aa_j\{G_a(t - T_{1j}) - G_a(t - T_{2j})\} \\
G_p(t) &= \alpha^2 t \exp(-\alpha t) \hspace{10pt} (t \geqq 0,\hspace{5pt} else\ 0) \\
G_a(t) &= \rm{min}[1 - (1 + \beta t)\exp(-\beta t),\ \gamma] \hspace{10pt} (t \geqq 0,\hspace{5pt} else\ 0)
\end{align}
のように、基底成分$F_b$、緩やかに減衰するフレーズ成分$F_p$、急峻に変化するアクセント成分$F_a$の3つの和で基本周波数$F_0$をモデル化しちゃう藤崎モデル(超ザックリ)の
各パラメータ $\boldsymbol{\theta} = {T_0,\ A_p,\ T_1,\ T_2,\ A_a,\ f_b}$ を推定しようという話。
パラメータ $\boldsymbol{\theta}$ から $F_0$ を推定するのが順問題、
観測した$F_0$からパラメータ $\boldsymbol{\theta}$ を逆推定するのが逆問題で、色んな賢者たちがこの逆問題を解いてきたけど
未だに完璧な手法は存在しないんじゃないかな〜(多分)。
ということで今回は
A novel approach to the fully automatic extraction of Fujisaki model parameters
を。
大まかな流れ
※発話区間毎に
① 前処理:無声区間とショートポーズの補間、マイクロプロソディの除去(MOMEL Modelを使う)
② ハイパスフィルタで微細成分(→アクセント成分)と概形(→フレーズ成分)に分解
③ フレーズコマンドの初期推定
④ アクセントコマンドの初期推定
⑤ Analysis-by-Synthesisで各パラメータの最適化
っていう感じ。
実装
①前処理:補間
MOMEL MODELが理解不能だったので(というか、確かF0の抽出過程的に今回は難しいから諦めたような記憶が・・・)、その通りにはやってません!!!
今回もWORLDのHARVESTで得られた$F_0$を使うので基本的には無声区間は補間されてる。
ただしショートポーズは存在する場合もあるので、やっぱりちゃんと補間は頭に入れておくべき(戒め)。
def interpolation(f0):
vuv = np.zeros(len(f0))
ix = np.where(f0 > 0)[0]
vuv[ix] = f0[ix] / f0[ix]
diff = vuv[1:] - vuv[:-1]
ix_down = np.where(diff==-1)[0]+1
ix_up = np.where(diff==1)[0]
for i in range(len(ix_down)):
ix1, ix2 = ix_down[i], ix_up[i]
a = (f0[ix1-1] - f0[ix2+1]) / (ix1 - ix2)
b = -a * (ix1 - 1) + f0[ix1-1]
f0[ix1:ix2+1] = a * np.arange(ix1, ix2+1) + b
return f0
発話区間毎に線形補間した。
自分はよくやるやり方で、
有声区間を1、無声区間を0になってるvuvなる変数を用意して、その後退差分を取る。
そうすると1から0になる(ショートポーズになる瞬間)と0から1になる(ショートポーズが終わる瞬間)のインデックスが簡単に得られる。
それぞれのインデックスは隣接するわけだから、その間を線形補間してあげる。
ショートポーズのオフセットとオンセットで1セット。オンセットとオフセットの順番ではないのに注意。
①前処理:マイクロプロソディの除去
今回もローパスフィルタで除去した。
def remove_mp(f0, period, n_taps=51, cutoff=10):
padd1, padd2 = np.zeros(n_taps) + f0[0], np.zeros(n_taps) + f0[-1]
f0_ = np.hstack((np.hstack((padd1, f0)), padd2))
fil = sl.firwin(numtaps=n_taps, fs=int(1./period), cutoff=cutoff, pass_zero=True)
f0_ = sl.lfilter(fil, 1, f0_)
f0_ = f0_[int(n_taps/2)+n_taps:len(f0)+n_taps+int(n_taps/2)]
return f0_
periodはF0のサンプリング周期(WORLDのデフォルトは0.005)。
発散しないまでもフィルタに通すと両端が大振りになるので最初にf0の両端を伸ばしておく。どれくらい伸ばすかはご自由に(?)
また、FIRフィルタはタップ数の半分だけ遅延するので、その遅延分を取り戻してあげる(最後の行)。
それとそれと、MOMEL Modelを使うとめっちゃ平滑化された近似曲線になるっぽいから
MOMEL Modelを使うのを諦めた私は「A METHOD FOR AUTOMATIC EXTRACTION OF MODEL PARAMETERS
FROM FUNDAMENTAL FREQUENCY CONTOURS OF SPEECH」の3次関数近次を施した。
②ハイパスフィルタで分解
前処理したF0をカットオフ周波数0.5Hzのハイパスフィルタに通す。
def highpass(f0=None, fs=None, n_taps = 125, cutoff=.5):
n_padding = int(n_taps/2)
padd1, padd2 = np.zeros(n_padding) + f0[0], np.zeros(n_padding) + f0[-1]
f0 = np.hstack((np.hstack((padd1, f0)), padd2))
my_filter = sp.signal.firwin(numtaps=n_taps, fs=fs, cutoff=cutoff, pass_zero=False)
f0_ = sp.signal.lfilter(my_filter, 1, f0)
return f0_[int(n_taps/2)+n_padding:len(f0)+n_padding+int(n_taps/2)]
発話区間毎に行う。多分
確かタップ数は著者のホームページでの解説記事に書いてあったような気がする。
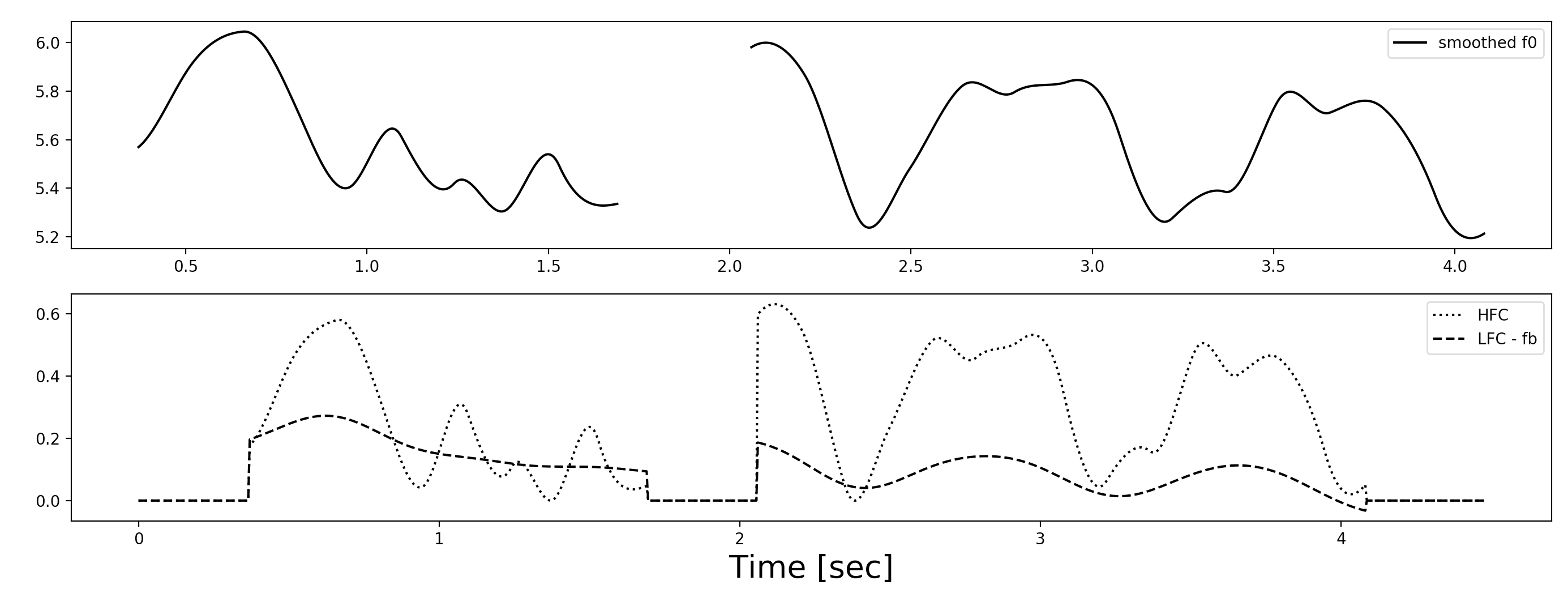
hfc = highpass(f0, 1./period)
offset_h = np.min(np.abs(hfc))
hfc -= offset_h
lfc = f0 - hfc
periodは何度も言うけどF0のサンプリング周期で、WORLDだとデフォルトで0.005 [sec]
それで、hfc(High Frequency Component)を得たら、その最小値を0に補正して
f0から減算してlfc(Low Frequency Component)もゲット。
ちなみに$f_b$はf0の最小値(0を除いて)
③フレーズコマンドの初期推定
まず、発話区間より1/$\alpha$ 秒前にT0を立てておく(論文では発話区間とドンのタイミングで立ててるけどアクセント指令もドンのタイミングで立つ可能性があるので。1/$\alpha$ の理由は、前回の記事の論文に倣った)。
LFCの極小値を探索して、そいつらを $T_0$ の候補生とする。
もし i-1番目の $T_0$ と1秒以上離れてたら、i番目の $T_0$ として合格させる。
candidate_T0 = scipy.signal.argrelmin(LFC[ix1:ix2+1])[0]
for i in range(len(candidate_T0)):
if candidate_T0[i] + ix1 - T0[-1] < th / period: # th/period => 1 sec
continue
else:
T0, Ap = estimate_i_command(T0, candidate_T0[i]+ix1, Ap, LFC, fb, time_axis)
発話区間毎にやる
ix1とix2は発話区間の頭とケツのインデックス
def estimate_i_command(T0, T0i, Ap, LFC, fb, time_axis, alpha=3.):
period = time_axis[1]
yp = trajectory_yp(Ap, time_axis[T0], time_axis)
res_contour = (LFC - yp)[T0i:]
candidate_max = scipy.signal.argrelmax(res_contour)[0]
if len(candidate_max) == 0: # none maxima => ref. max val
ix_max = np.argmax(res_contour)
else: # else => ref. maxima val
ix_max = candidate_max[0]
max_val = res_contour[ix_max]
Api = np.exp(1)/alpha * (max_val - fb)
T0i = ix_max + T0i - int(1./alpha/period)
return np.hstack((T0, [T0i])), np.hstack((Ap, [Api]))
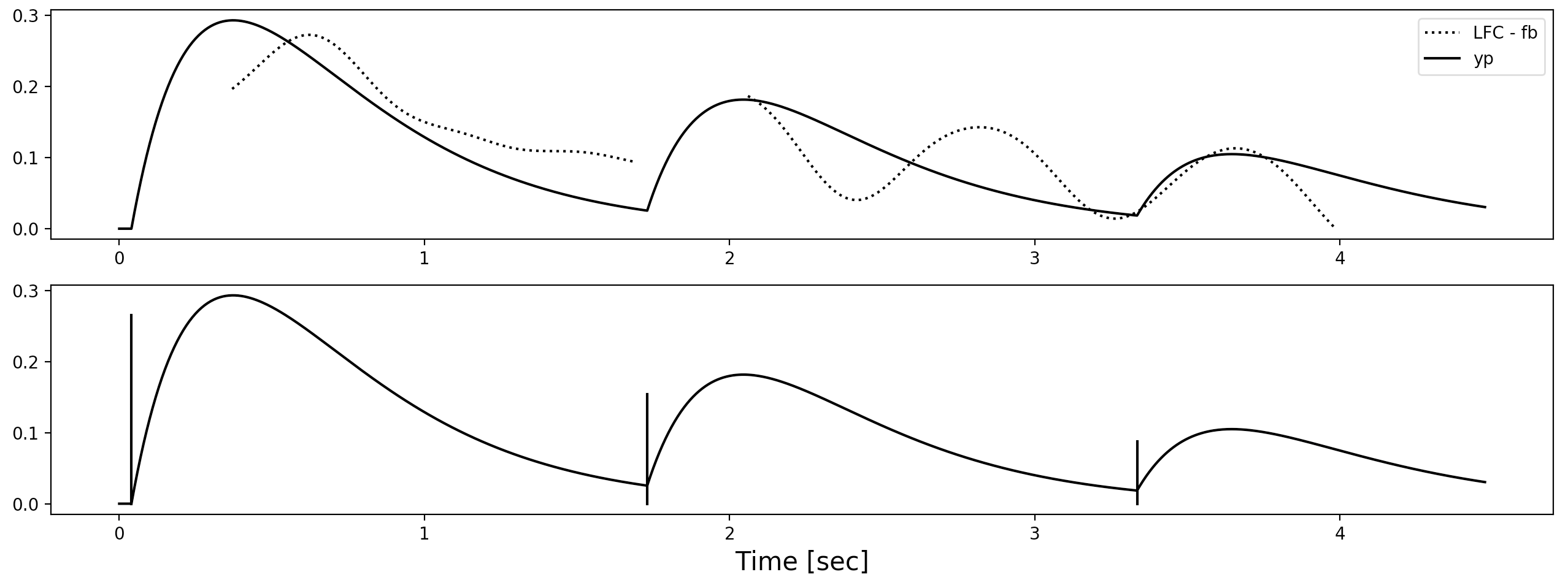
trajectory_yp()は既知パラメータで推定されるフレーズ成分を算出する自作関数です。
まず、i番目のT0候補から、Apも推定する。
i番目のT0の直後にくるLFC - yp残差の極大値を探す。
その極大値とi番目のフレーズコマンドが作るであろう曲線の最大値が一致するようにApを算出する。
このとき、残差のres_contourはi-1番目までのT0とApを用いたフレーズ成分を引いたものとする(※先行するフレーズ指令の影響も受けるため)。
忘れずにやっておきたいのが、参照するres_contourの最大値からfbを引いておくこと。
フレーズ成分はLFC - fbなので。
そんでもってついでにT0も少しいじっておく。
最大値は一致するようにApを選んだけど、実は時間位置はいい加減なので
最大値を取るタイミングも一致するようにT0も調整しておく(ここは論文に載ってない自己流だけど)。
フレーズ指令同士が1秒以上離れるっていう制約のせいで1つ山を取りこぼしてるぅ!
④アクセントコマンドの初期推定
HFCの極小値を求めて、そいつらがT1及びT2の候補生たちになる。
つまり、HFCの極大値がアクセント成分に対応するから、その極大値を囲む極小値たちがアクセントの始まりと終わりを担うだろうっていう狙い。
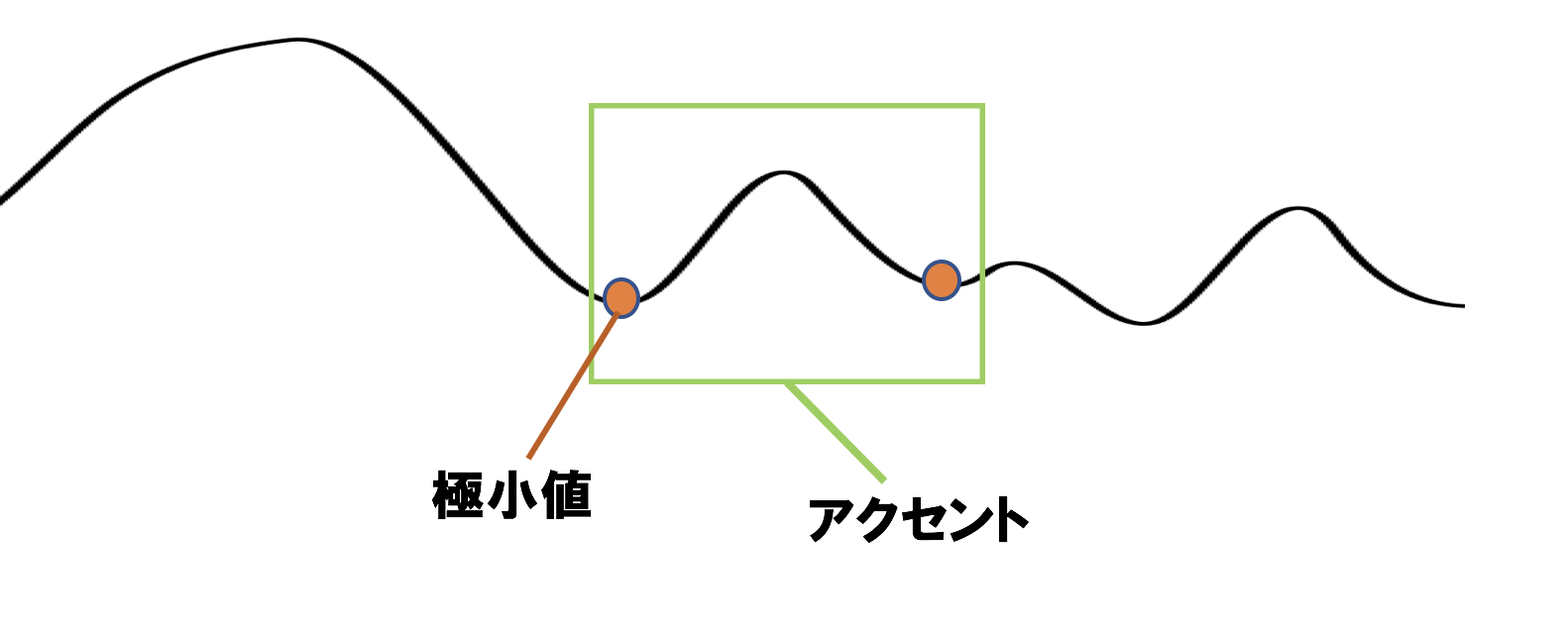
極小値の周辺200msの範囲で最小値を探索して、その最小値を取る時刻をj番目のT1として合格させる。
T2はj+1番目のT1より200ms戻った位置にする。
論文では周辺100msの範囲でT1を調整してるが、著者のホームページ上の解説記事では200msにしてるからそれに倣った。
Q.もし極小値じゃなく極大値が最初に検出されたら、T1どうするの?
A.論文では特に記述ないけど暫定的に発話区間の先頭にしておく。
Q.もし極小値じゃなく極大値で終わったら、T2どうするの?
A.論文では特に記述ないけど暫定的に発話区間のケツにしておく。
振幅はこんな感じ
def initialize_Aa(HFC, T1, T2, time_axis):
J = len(T1)
Aa = np.zeros(J)
dammy_T1 = np.hstack((T1, [len(time_axis)]))
for j in range(J):
ya = trajectory_ya(Aa, time_axis[T1], time_axis[T2], time_axis)
res_contour = (HFC - ya)[T1[j]:dammy_T1[j+1]]
ref_maxima = np.max(res_contour)
Aa[j] = 1.0
ya_tmp = trajectory_ya(Aa, time_axis[T1], time_axis[T2], time_axis)
ya_tmp_maxima = np.max(ya_tmp[T1[j]:dammy_T1[j+1]])
Aa[j] = (ref_maxima / ya_tmp_maxima)
return Aa
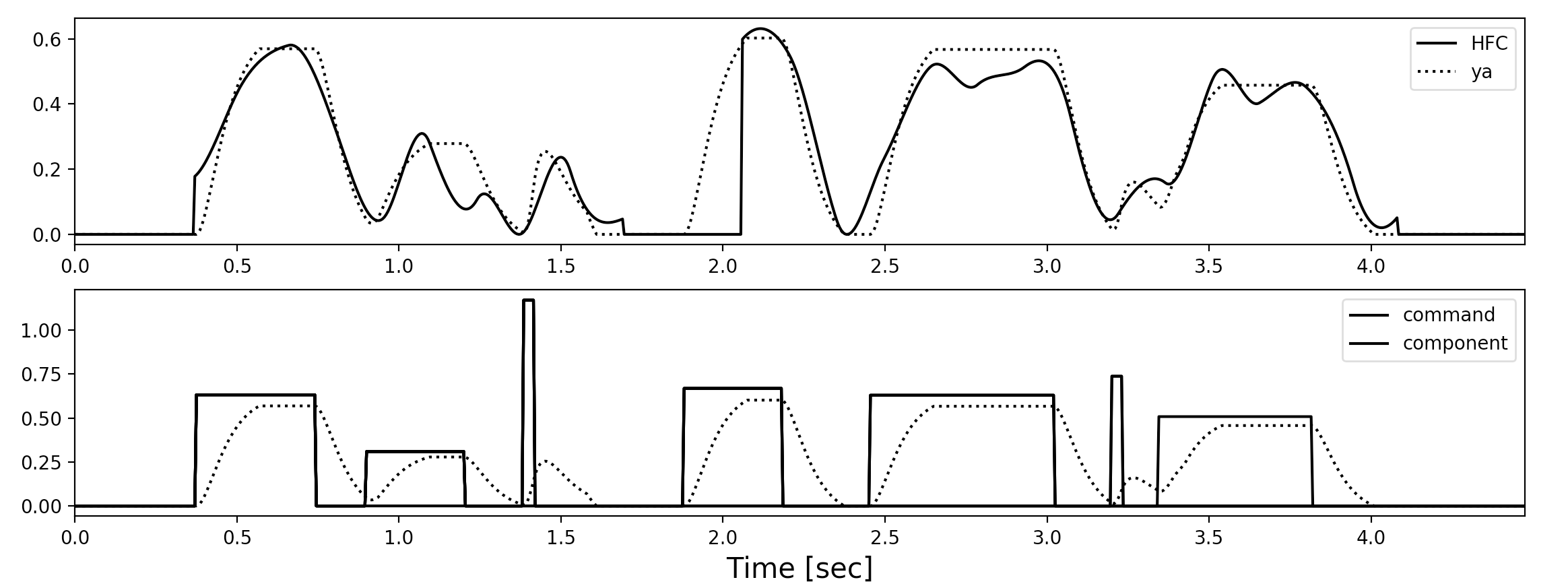
フレーズ指令のときとは違って、今回は解析的に暫定的なフレーズ成分の極大値は求められないので
シンプルに最大値が一致するようにした。
そのために暫定的にj番目の振幅Aaを1.0にしてる。
3番目と6番目の指令の振幅がデカすぎてバグかと思ったけど違います〜
指令のdurationが短いせいで、上昇途中で下降しないといけないため、
一瞬の上昇で所望の高さを得るために振幅がデカくないといけないんだと理解した(^◇^)
⑤最適化
今回の手法ではフレーズ指令とアクセント指令を独立して初期推定したので
"あらゆる指令も、ONになってる最中に他の指令がONになることはない"という制約を破る可能性がある。
本来はアクセント指令が発動中にフレーズ指令が立ち上がっちゃいけない。
つまり、$T_{1j} \le T_{0i} \le T_{2j}$ であってはいけないということ。
def constraint(T0, T1, T2, Aa):
I = len(T0)
for i in range(I):
T0i = T0[i]
J = len(T1)
for j in range(J):
if T1[j] < T0i and T2[j] > T0i:
T2 = np.insert(T2, j, T0i - 1)
T1 = np.insert(T1, j+1, T0i+1)
Aa = np.insert(Aa, j+1, Aa[j])
return T1, T2, Aa
ここも制約をどうするか論文に記載なかったけど
とりあえず $T_{0i}$ の位置でぶった切って アクセント指令を両断した。
T0とT1を時系列順にごちゃまぜに一列に並べて順に最適化していく。
スタンスは
その指令が影響を及ぼす時間t1〜t2内で平滑化F0と再合成F0の差が小さくなるように山登り法で調整する感じ。
山登り法は、パラメータを微小変化させて最も誤差が少なかった変化パターンを採用するやつ。
微小変化は1にした(つまり、1下げるか停滞か1上げるかの3パターン)。
重要なのはt1とt2を決めるのと、調整と言っても行っちゃいけない境界線を決めること。
フレーズ指令
t1は立ち上がり位置(つまり $T_{0i}$ そのもの)か発話区間の頭になる。
$T_{01}$とか第二発話区間の最初のフレーズ指令は、発話区間に先行して立ち上がるので
再合成F0では本来F0が存在しない範囲に仮想的に値が存在することになる。
それなのに"平滑化F0と再合成F0の差が小さくなるように"というのも破綻するので
発話区間最初のフレーズ指令に関しては立ち上がり位置じゃなくて発話区間の頭に設定すべきかと。
t2は当該発話区間のケツとする。
(本当は緩やかに減するするのでもっとちゃんと考えないといけないけど面倒だから・・・ごめんさいママ)
$T_{0i}$の許容変化幅は、
左側は ①「max (0, $T_{0i} - 100$) 」、②「直前の発話区間の終点+30」、③「$T_{0i-1} + 1$」、④「$T_{2j} + 1」のどれかに。
①は発話区間最初のフレーズ指令の場合。100は適当。負になったら困るから0でセーフティーかけておく。
②は第二〜発話区間最初のフレーズ指令の場合。直前の発話区間内に入らないようにしたけど実際は入ってもいいのか?知らん。30も適当。知らん。
③は直前がフレーズ指令の場合
④は直前がアクセント指令の場合
右側は①「当該発話区間終点」、②「次の指令の立ち上がり地点-1」のどれかに。
①は $T_{0i}$ が当該発話区間内、最後の指令だった場合
②は ①じゃないとき。
振幅 $A_{pi}$ は勾配法で更新する。
アクセント指令
t1は立ち上がり位置か当該発話区間の頭とする。
t2は①「当該発話区間終点」か、②「右隣の指令の立ち上がり位置-1」に。
①は当該発話区間最後の指令の場合
②は①じゃない場合
$T_{1j}$の許容変化幅は、 左側は①「max($T_{1j}$ -100, 0)」、②「直前のフレーズ指令立ち上がり位置+1」、③「$T_{2j-1}$ + 1」のどれかに。 >①はまず無さそうだけど最初の指令がアクセント指令の場合。100は適当 >②は左隣の指令がフレーズ指令の場合 >③は左隣の指令がアクセント指令の場合
右側は$0.5 * (T_{1j} + T_{2j})$とする。
$T_{2j}$の許容変化幅は、
左側は$0.5 * (T_{1j} + T_{2j})$
右側はt2
振幅はさっき同様に勾配法で。
ということで、一列に並べたT0とT1たちを左から1つずつ取って、
t1とt2、教養変化幅を決めたら・・・
山登り法でベストな変化パターンを決めて、
もし許容変化幅を超えたら停滞にして更新します。
もし更新した後、$T_{1j}$と$T_{2j}$の距離が10ms未満になったらそのアクセント指令は削除する。
特に論文で記載ないけどただの棒みたいなアクセント指令は要らんやろっていう。
結果
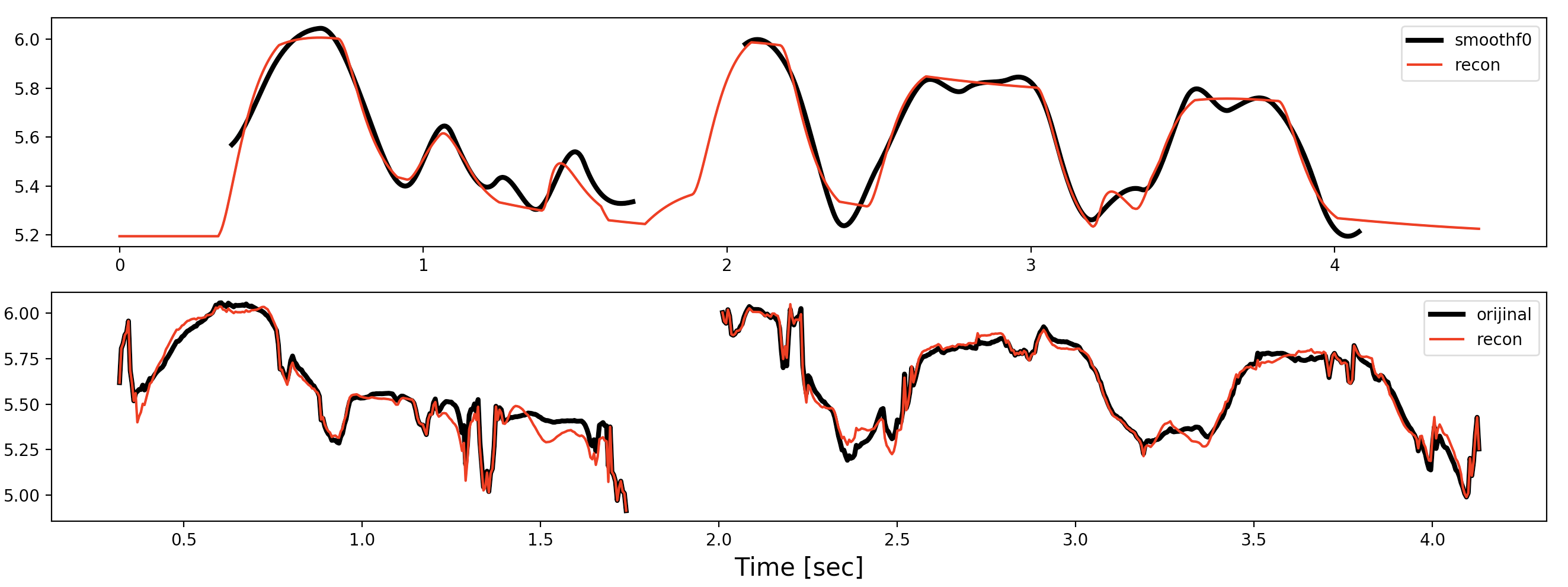
上段がsmoothf0と再合成f0で
下段がオリジナルf0の対数と再合成f0
に残差を復元したやつ。
残差は
zansa = np.log(f0) - smoothf0
recon_f0 += zansa
終わり
個人的には前回の手法より今回の手法の方が好きです。
前回のやつは手法を再現するにはわからない箇所が多かったですが、
今回の手法はわからないところは有っても「よきにはからえ」感があって別に精度に大きく影響するようなものではなかった気がします。
また、最初にハイパスフィルタで成分を分解しましたが、
前回の記事で暑かった論文では「フィイルタ処理で適切にアクセント/フレーズ成分を分離できる保証がない」と指摘されており、それはごもっともだとは思います。
僕はこの手のエキスパートではないので推定した指令が正しいかどうかの判断はできない(エキスパートたちはF0軌跡を見て手動で指令をラベリングするので最後に精度の検算ができますが)のでなんとも言えませんが。
間違いや質問などありましたらいつでもお願いします。