エンジニアに転職して早2年半。いまだに再帰関数が苦手です。
再帰関数を含むコードレビューがあると「よく分からんけど、動作も良いしテストも書かれてるしヨシ!!approved!!」としてしまったことも...(絶対あかん😇)。
さすがにそれはヤバイと、再帰関数を学び直したのでその結果をまとめてみました。
再帰関数とは?
再帰関数とは、関数内で、自分自身を呼び出す関数です。
この時点で謎ですよね。最初にみたときは「無限ループでは?」って思いました。
以下再帰関数の例として度々あげられる階乗の計算です。
const factorial = (n: number): number => {
if (n < 2) {
return 1;
}
return n * factorial(n - 1);
};
factorial関数内で、return n * factorial(n - 1)と自分自身を呼び出しています。
この関数の結果は以下テストの通りです。
test('factorial' => {
expect(factorial(0)).toBe(1);
expect(factorial(1)).toBe(1);
expect(factorial(3)).toBe(6);
expect(factorial(5)).toBe(120);
expect(factorial(8)).toBe(40320);
})
確かに期待値通り、階乗を計算できていますね。
次項以降で再帰関数のコードを読む際のポイント、再帰関数での実装に向いている処理をまとめていきます。
再帰関数を読むためのポイント
まず、コードリーディングで再帰関数を読み解くときに意識すると良いことをまとめます。
基本ケースと再帰ケースで処理を分けて考えてみる
再帰関数内の処理は、自分自身を呼び出さない基本ケースと、自分自身を呼び出し再帰的に処理する再帰ケースの2つに分かれています。
それを意識しながらコードを読むと、どのタイミングで処理を抜けるのか分かり再帰関数が無限ループにならないことが理解できます。
先ほどの階乗の例でみると以下の通りです。
const factorial = (n: number): number => {
if (n < 2) {
return 1; // ⭐基本ケース
}
return n * factorial(n - 1); // ⭐再帰ケース
};
if (n < 2) {}のif文で基本ケースと再帰ケースを分けているのが分かります。
再帰ケースにて引数のnは1ずつ減少していくので処理を繰り返せばいずれ、n < 2の条件を満たします。
そうすると基本ケースに移動し、実際の値を返します。
基本ケースがない、もしくは基本ケースにたどり着かないケースがある再帰関数は処理が終わらずスタックオーバーフローに陥るので、再帰関数を書く際にも基本ケースと再帰ケースを分けて考えると良いと思います。
コールスタックをイメージしてみる
次に実際にどのように処理されるのかをイメージするポイントです。
プログラムでは関数を呼び出すと、関数自身のローカル変数等を保持するフレームが生成されてコールスタックと呼ばれるスタックにpushされます。そして、関数の評価が完了するとコールスタックからpullされます。
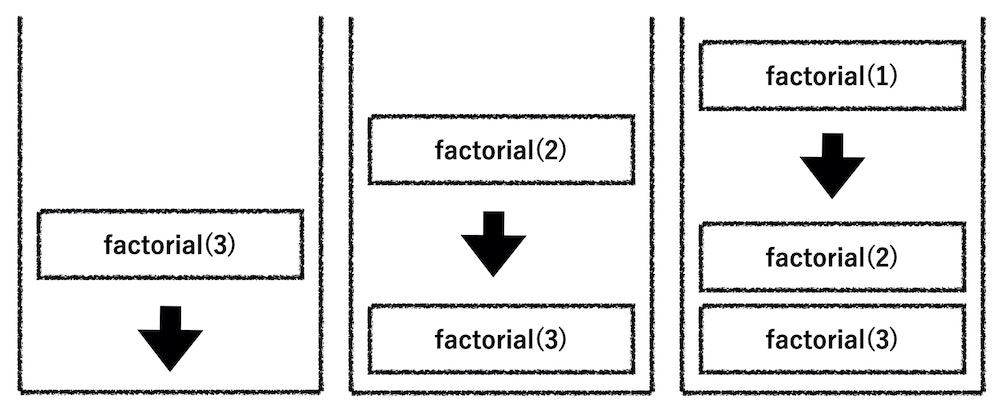
その流れを再帰関数で考えてみましょう。以下は、factorial(3)のケースのコールスタックを図にしています。
まず最初に、factorial(3)がそのままスタックにpushされて、その後factorial(3)を処理すると戻り値はfactorial(2)でまだ計算結果を取得できないので、さらにfactorial(2)スタックにpushされます。同じくfactorial(2)の戻り値にもfactorial(1)が含まれるので、factorial(1)がスタックにpushされます。
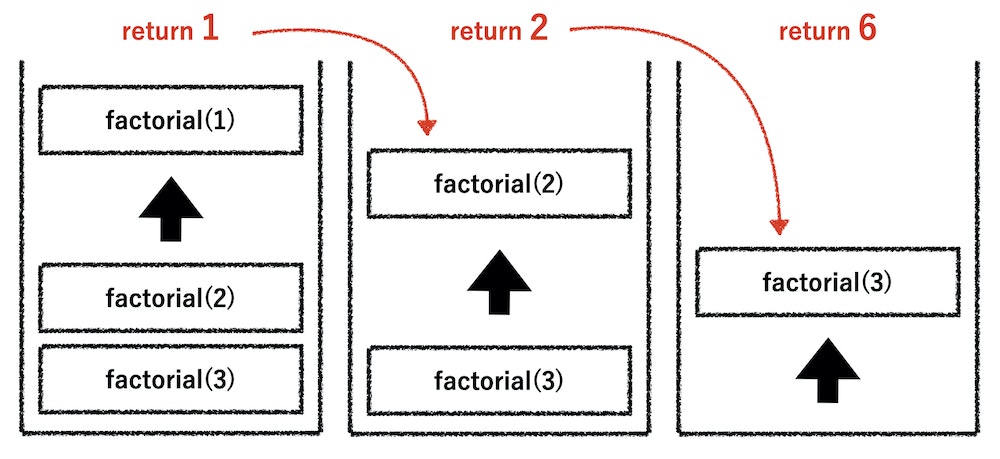
factorial(1)の処理は、基本ケースで1を返すのでfactorial(1)はpullされて次のfactorial(2)に戻り値である1を渡します。さらに、factorial(2)ではその1を使って計算ができるのでpullされて、戻り値の2をfactorial(3)に渡します。最後に、factorial(3はその戻り値の2を使って計算され6という結果を返します。これでコールスタックがきれいに空になります。
基本的にどの再帰関数もコールスタックに関数がどんどん積まれて、基本ケースになったら上から順に解決されていくという流れは同じです。
処理が追えなくなったら、一度コールスタックの図を書いてみると腹落ちするかもしれません。
評価結果を愚直に書き出してみる
コールスタックの図以外にも理解を助けるものとして評価結果を愚直に書き出してみるのもおすすめです。
実際にfactorial(4)の時の評価結果を書き出すと以下のようになります。
factorial(4)
=> 4 * factorial(3) // factorial(4)の時のreturn値
=> 4 * (3 * factorial(2)) // factorial(3)の時のreturn値
=> 4 * (3 * (2 * factorial(1))) // factorial(2)の時のreturn値
=> 4 * (3 * (2 * (1))) // factorial(1)の時のreturn値
=> 4 * 3 * 2 * 1 // カッコを外すと階乗の計算になっている!
=> 24 // 結果
実際に順を追って評価結果を書き出してみると最終的には階乗の計算式になっていることがわかると思います。
引数に与える値を基本ケース付近にして評価結果を愚直に書き出すことで処理をイメージしやすくなるはずです。
再帰関数が向いている処理は?
再帰関数の大体のイメージがついたところで、どのようなときに再帰が有効なのか?というのを考えてみます。
漸化式で表せる処理
ひとつは漸化式で表せるものです。ここでいう漸化式は以下Wikipediaの定義の通りです。
漸化式(ぜんかしき、英: recurrence relation; 再帰関係式)は、各項がそれ以前の項の関数として定まるという意味で数列を再帰的に定める等式である。
数列を再帰的に定める等式 と、説明からして再帰関数に関係してそうですね。
単純な漸化式で表せるものは、漸化式の数式を割とそのままコードに落とせば再帰関数が出来上がります。
よく再帰関数の例であげられるフィボナッチ数列はまさにそれですね。
フィボナッチ数列は「前の2つの数を足したものが次の数になるという規則に基づいている数列」です。黄金比やひまわりの種の螺旋構造との関連とかの話が有名です。
フィボナッチ数列は以下漸化式で表せます。
$F_0 = 0$,
$F_1 = 1$,
$F_{n+2} = F_n + F_{n+1} (n ≥ 0)$
これを変換してn番目のフィボナッチ数を出す公式は以下の通りです。
$F_0 = 0$,
$F_1 = 1$,
$F_n = F_{n-1} + F_{n-2}$
これをそのままコードに落とし込むと再帰関数の出来上がりです。
const fibonacci = (n: number): number => {
if (n < 2) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
};
nが2未満の時は、nの値をそのまま返し(基本ケース)、それ以上の場合は$F_{n-1} + F_{n-2}$を返しています(再帰ケース)。
このように漸化式で表せるものは比較的容易に再帰関数として定義できます。そのような要件が出てきたら一度再帰で処理できるか考えてもよいかもしれません。
木構造を取り扱う処理
次に、木構造(枝分かれしながらデータが伸びていくデータ構造。ネストしているオブジェクト型など)のデータの各要素になんらかの変更を加える処理は再帰関数で有効です。
1つの階層に与える処理の中で、さらに階層が見つかったら自分自身を呼びだすという形ですね。
割と業務で扱うことが多いオブジェクトのケース変換処理(snake to lowerCamel)を例にみてみます。
実装コードは以下の通りです。
// スネークケースの文字列のキャメルケースへの変換を行う関数
// 再帰ではないので、今回は特に処理内容は見なくて大丈夫です
const camelize = (str: string) => {
return str.split("_").reduce<string>((acc, cur, i): string => {
if (i === 0) {
return cur.toLowerCase();
}
return acc + cur.charAt(0).toUpperCase() + cur.slice(1).toLowerCase();
}, "");
};
// オブジェクトを受け取り、key名にcamelizeを適応する関数
const camelCaseDeep = (obj: Record<string, any>) => {
const result = {} as Record<string, any>;
Object.keys(obj).forEach((key) => {
if (Object.prototype.toString.call(obj[key]) === "[object Object]") {
obj[key] = camelCaseDeep(obj[key]); //⭐ ここで再帰的に実行している
}
result[camelize(key)] = obj[key];
});
return result;
};
camelCaseDeepがオブジェクトを受け取り再帰的に全てのキー名をsnakeケースからlowerCamelケースにケース変換しています。
ここでのポイントは、今までの例とは逆で基本ケースが、if文の外にあり再帰ケースがif文の中にあるという点です。探索中にオブジェクト型が見つかった場合のみ、さらに自分自身を再帰的に呼び出しています。
この関数では何層もネストしたオブジェクトでも全てのキーをケース変換可能です。これを再帰関数ではなく通常のループで書こうと思うとかなり大変です。
なので、ネストした木構造のデータを扱う場合は最初から再帰でトライしてみても良いかもです。
再起関数を書く際に注意すべきこと
最後に再帰関数を実装するうえで注意すべきことをまとめます。
計算量の増加
再帰関数は簡潔に処理をかけるのですが、往々にして通常のループに比べて計算量が増加しがちです。
例えば例にあげたフィボナッチ数を求めるfibonacci関数は1つの数値を出すのに内部で2つのfibonacci関数を実行しているので、計算量は$O(2^n)$となります。これでは入力が増えると指数関数的に計算量が増加してしまいます。
実際にChromeでfibonacci(50)を実行するとしばらく結果が帰ってきません。
これには対策としてはメモ化があります。
メモ化は再帰関数内で重複する呼び出し結果を保存しておいて、計算量の増加を防ぐ方法です。fibonacci数の計算の場合は、以下のように改善できます。
const fibonacci = (n: number, memo: number[] = []): number => {
if (n < 2) {
return n;
}
if (memo[n]) {
return memo[n];
}
return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo);
};
fibonacci関数の第2引数にmemoという配列を追加し、デフォルトで空配列を渡しておきます。そして、fibonacciの計算結果をmemoに毎回蓄積していきます。
一度呼び出されたfibonacci(n)の結果はmemo[n]に保存されているので、再度スタックに積まれることなく処理可能となり、計算量が$O(n)$まで減ります。
実際にChromeで実行した場合、通常のfibonacci関数だとfibonacci(50)で結果がなかなか返ってきませんが、memo化を行った場合fibonacci(1000)でも一瞬で計算できました。
実装するときは再帰関数の計算量がどのようになるのか?メモ化は適応できないのか?一度考えた方が良いと思います。
スタックオーバーフロー
最後に、再帰関数に必ずついて回るのがスタックオーバーフローです。
スタックオーバーフローとはコールスタックに処理が積み上がりすぎて、メモリ領域が足りなくなり、プログラムが異常終了することです。
再帰はコールスタックをイメージしてみるで説明した通りスタックを使います。再帰が深くなれば深くなるほどスタックが積み上がり最終的にスタックオーバーフローを引き起こすので注意が必要です。
例えば例としてあげていた階乗を計算するfactorial関数の場合は、Chromeでfactorial(13000)を実行するとMaximum call stack size exceededとスタック・オーバーフローが発生します。

その対策としては、末尾再帰化があります。
末尾再帰とは再帰関数のうち、自分自身の呼び出しが末尾呼び出し(return時、最後に評価される処理)となっている再帰関数です。
末尾再帰の再帰関数を、末尾再帰最適化を行ってくれる実行環境で実行すると、余計なスタックが積まれず、スタックオーバーフローが発生しなくなります。
末尾再帰化したfactorial関数はこちらです。
第2引数のaccumに計算結果が蓄積され、基本ケースでaccumを返すように修正されています。
const factorialTailCall = (n: number, accum: number = 1): number => {
if (n === 0) {
return accum;
}
return factorialTailCall(n - 1, n * accum);
}
現状のブラウザが末尾再帰最適化に対応していないため、実行結果の確認は出来ていないのですが、末尾再帰最適化に対応した実行環境だとおそらくスタックオーバーが発生しないはずです。
末尾再帰化について、私自身なかなか曖昧な理解なのでより詳しい説明はこちらの記事を参照してください。
終わりに
以上、「再帰関数が苦手なエンジニアのための再帰関数入門」でした。
正直自分自身まだまだ全然自信はないのですが、記事まとめる段階で少しは理解が進んだので書いて良かったかなと思ってます。自分のように「再帰関数ぅぅ..😭」となっている人の少しでも助けになれば幸いです。
また、もし記事中に誤り等あれば、マサカリ🪓 優しさあるコメントで教えてもらえると嬉しいです。