はじめに
プロモーション活動を行う際などにクラスタリングをすることがありますが、その手法はたくさんあります。
例えば、k-meansや混合ガウス分布などもその1つです。
今回は階層的クラスター分析に焦点をあて、その計算方法をまとめます。
階層的クラスター分析の仕組み
階層的クラスター分析(hierarchical clustering)は、似た特徴を持つデータをグループにまとめていく手法です。
具体的に身長と体重のデータを使って、この分析の基本的な仕組みを簡単に説明してみましょう。
例:4人の身長と体重のデータ
人1: 身長160cm, 体重60kg
人2: 身長170cm, 体重65kg
人3: 身長175cm, 体重80kg
人4: 身長180cm, 体重75kg
手計算で階層的クラスター分析を実行するステップ
ステップ1: 距離の計算
まず、各個人間の「距離」を計算します。この例では、ユークリッド距離を用いますが、他にもマンハッタン距離など様々な距離の計算方法があります。
ユークリッド距離の公式は次のようになります
距離 = (身長差)^2 + (体重差)^2
実際に上記のデータで距離を計算し、どのようにクラスタリングが進むか見てみましょう。
計算された距離は以下のようになります(小数点以下は簡略化して表示):
人1と人2の距離: 11.18
人1と人3の距離: 25.00
人1と人4の距離: 25.00
人2と人3の距離: 15.81
人2と人4の距離: 14.14
人3と人4の距離: 7.07
ステップ2: クラスターの形成
次に距離が最も近いペアからクラスターを形成します。このステップを繰り返し、全てのデータが一つのクラスターになるまでグループ化します。
※一般的には、単リンケージ(最小距離)、完全リンケージ(最大距離)、平均リンケージ(平均距離)などの方法がありますが、ここでは単リンケージ(最小距離)を使用します。
最も距離が短いペア、人3と人4の距離が7.07なので、最初にこの二人をグループ化します。そして、残りの人々とこの新しいグループ間の距離を計算し直します。
新しい距離を計算して、次のグループ化を見てみましょう。新しい距離行列は次のように更新されます
人1と人2の距離: 11.18(変更なし)
人1と人3-4クラスタの距離: 25.00
人2と人3-4クラスタの距離: 14.14
次に最も距離が短いのは、人1と人2の間で11.18です。これらをグループ化します。
最後に、新しく形成された人1-2クラスタと人3-4クラスタをグループ化します。
ステップ3: デンドログラムの作成
クラスタリングの過程を可視化するために、デンドログラム(樹形図)と呼ばれる図を描きます。これによって、どのデータがどのステップで結合されたかがわかります。
ライブラリを使用しないサンプルコード
これまで説明した工程をnumpyとpandasのみで実装すると以下のようになります。
import numpy as np
import pandas as pd
# データの初期化
data = pd.DataFrame({
'身長': [160, 170, 175, 180],
'体重': [60, 65, 80, 75]})
# ユークリッド距離の計算関数
def euclidean_distance(row1, row2):
return np.sqrt(np.sum((row1 - row2) ** 2))
# 距離行列の初期化
def init_distance_matrix(data):
num_samples = data.shape[0]
distance_matrix = np.zeros((num_samples, num_samples))
for i in range(num_samples):
for j in range(i + 1, num_samples):
distance = euclidean_distance(data.iloc[i], data.iloc[j])
distance_matrix[i, j] = distance
distance_matrix[j, i] = distance
return distance_matrix
# クラスタリングの実行
def hierarchical_clustering(data):
clusters = [{i} for i in range(data.shape[0])]
distance_matrix = init_distance_matrix(data)
steps = []
while len(clusters) > 1:
min_distance = np.inf
pair_to_merge = None
# 最小距離のペアを見つける
for i in range(len(distance_matrix)):
for j in range(i + 1, len(distance_matrix)):
if distance_matrix[i, j] < min_distance:
min_distance = distance_matrix[i, j]
pair_to_merge = (i, j)
# クラスタをマージ
new_cluster = clusters[pair_to_merge[0]].union(clusters[pair_to_merge[1]])
new_clusters = [c for k, c in enumerate(clusters) if k not in pair_to_merge]
new_clusters.append(new_cluster)
clusters = new_clusters
# 距離行列を更新
new_distance_matrix = np.full((len(clusters), len(clusters)), np.inf)
for i in range(len(clusters)):
for j in range(i + 1, len(clusters)):
distances = [distance_matrix[p, q] for p in clusters[i] for q in clusters[j] if p != q]
new_distance_matrix[i, j] = new_distance_matrix[j, i] = min(distances)
distance_matrix = new_distance_matrix
steps.append((clusters[:], min_distance))
return clusters, steps
# クラスタリング実行
final_clusters, clustering_steps = hierarchical_clustering(data)
final_clusters, clustering_steps
ライブラリを使用したサンプルコード
Pythonで階層的クラスタリングを簡単に実装するには、SciPyライブラリが非常に便利です。
SciPyのscipy.cluster.hierarchyモジュールには、データセットを階層的にクラスタリングするための関数が含まれています。
このセクションでは、先ほどの例をSciPyを使ってどのように処理するかを説明します。
必要なライブラリのインポート
import numpy as np
import pandas as pd
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
データの準備
先ほどと同じデータをDataFrameとして準備します。
data = pd.DataFrame({
'身長': [160, 170, 175, 180],
'体重': [60, 65, 80, 75]
})
階層的クラスタリングの実行
SciPyのlinkage関数を使用して、階層的クラスタリングを実行します。
ここでは、'ward'メソッドを使用していますが、'single'(最短距離法)、'complete'(最長距離法)、'average'(平均距離法)など他の方法も選択可能です。
# データから距離行列を計算してlinkageを実行
Z = linkage(data, method='ward')
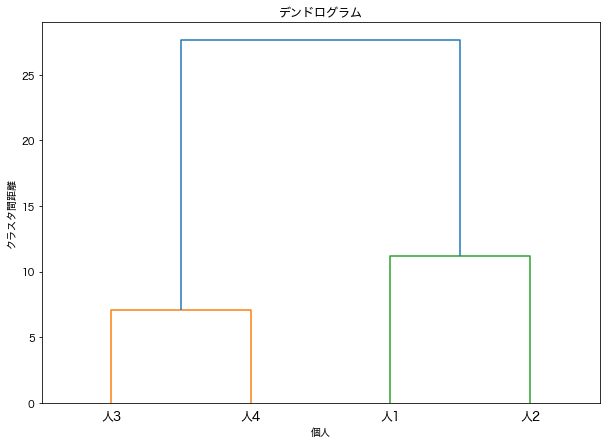
# デンドログラムの表示
plt.figure(figsize=(10, 7))
dendrogram(Z, labels=['人1', '人2', '人3', '人4'])
plt.title('デンドログラム')
plt.xlabel('個人')
plt.ylabel('クラスタ間距離')
plt.show()
このコードを実行すると、データの階層的クラスタリングの過程を示すデンドログラムが生成されます。
デンドログラムでは、x軸には個人が、y軸にはクラスタ間の距離が表示され、どのデータがどのタイミングでクラスターに統合されたかが視覚的にわかります。
最後までお読みいただきありがとうございました!