皆さんこんにちは!Ruteです!
この記事は、AtCoder Beginner Contest 176の問題のC問題の解説になります!!
A問題・B問題の解説を見ていない方は、以下の表で示したリンクよりご確認下さい。
各問題・解説へのリンク
| A | B | C |
|---|---|---|
| ABC176 A | ABC176 B | この記事です!! |
それでは、C問題の解説を始めます。
問題概要
$N$人が1列に並んでいて、前から$i$番目の人の身長は$A_i$である。
それぞれの人の足元に、高さ$0$以上の踏み台を設置し、全ての人が以下の条件を満たすようにしたい。
条件:
(自分の身長と)踏み台を込めて身長を比較したとき、自分より前に、自分より背の高い人が存在しない
この条件を満たすときの、踏み台の高さの合計の最小値を求めよ。
問題URL : https://atcoder.jp/contests/abc176/tasks/abc176_c
制約
・$1 \leq N \leq 2×10^5$
・$1 \leq A_i \leq 10^9$
・入力は全て整数
解法
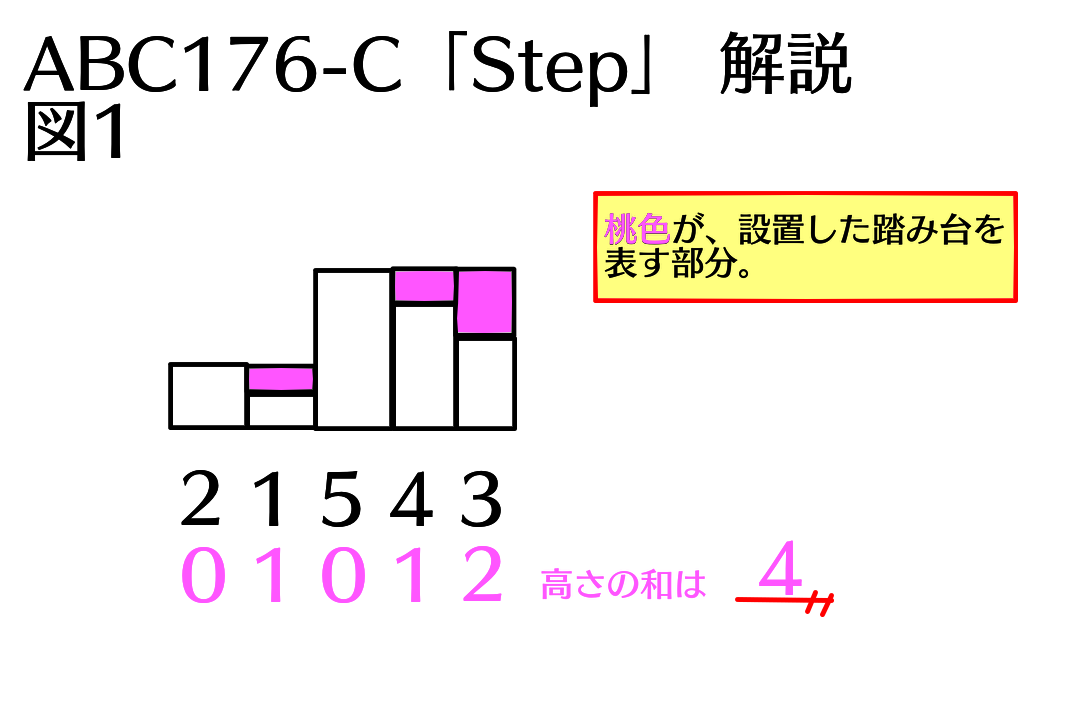
入力例1について考えます。
自分より前に、自分より背の高い人が存在しない ということですから
⇔自分より背が高い人が前にいたら、背が高い人に身長を合わせる
ということをすれば、踏み台の高さを最小に出来そうです。
入力例2では、全員が同じ高さなので、踏み台の高さは0で、和も0になります。
自分より背が高い人が前にいたら、背が高い人に身長を合わせる という条件は以下の条件に言い換えることが出来ます。
$A_1,A_2,...A_N$という数列のうち、単調減少の部分のみで、前の人と同じ身長になるように踏み台の高さを調整すればよい
例えば、単調増加の数列の場合、自分の後ろには自分より高い人しかいないわけですから、
これは踏み台の高さを調節する必要がなくなります。
図2のように、ある人Xの前に高い人がいて、Xの後ろにいる人と身長が同じ場合、Xと、その後ろにいる人の両方の踏み台の高さを調整しなければなりません。
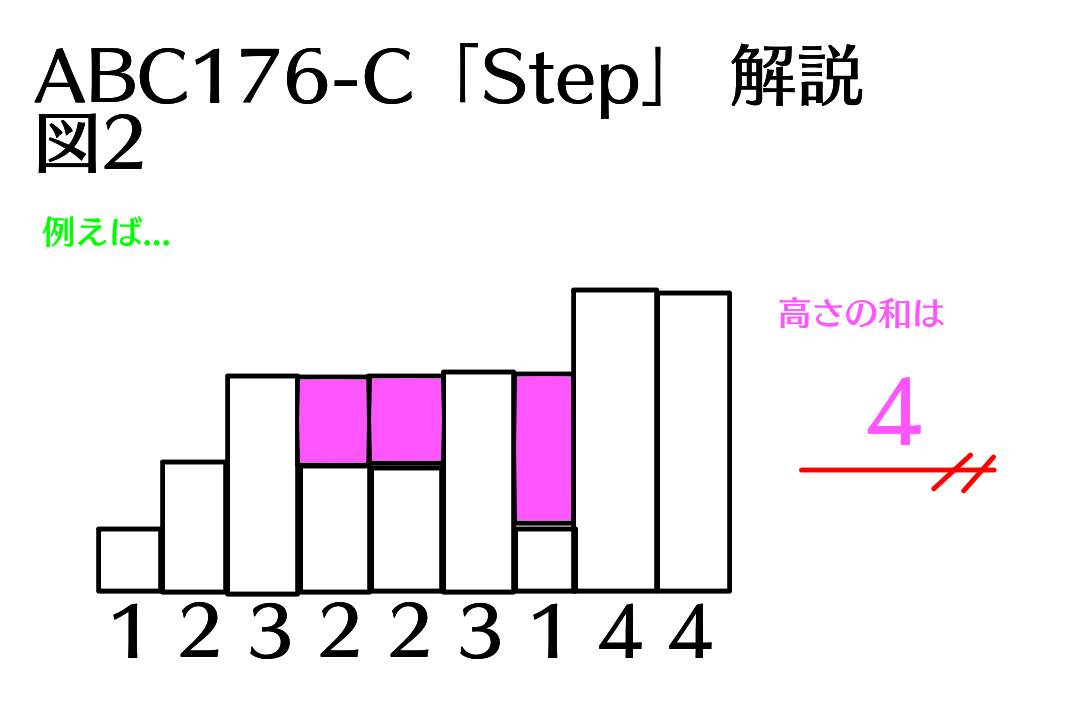
したがって、以下の様な処理を行えば良いでしょう。
処理
ansを最終的な答えの値として定義し、$0$で初期化します。
iの範囲を(1,N-1)として以下の様なループを回します。
A[i-1] > A[i]ならばansにA[i-1]-A[i]の差を足し、A[i]をA[i-1]の値と同じにする(前の人と踏み台の高さを同じにする)
最後にansを出力します。
計算量は$O(N)$です。
以下、Python3,C++,Javaでの解答例を示します。
各言語解答例(Python3,C++,Java)
Python3での解答例
N = int(input())
A = list(map(int,input().split()))
ans = 0
for i in range(1,N):
if A[i-1] > A[i]:
ans += A[i-1]-A[i]
A[i] = A[i-1]
print(ans)
C++での解答例
# include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++){
cin >> a[i];
}
long long int ans = 0;
for (int i = 1; i < n; i++){
if (a.at(i-1) > a.at(i)){
ans = ans + (a.at(i-1)-a.at(i));
a.at(i) = a.at(i-1);
}
}
cout << ans << endl;
return 0;
}
ansの値が$2×10^9$を超える可能性があるので、ansの型はlong long intにしましょう。
(∵ $2^{31}-1 \simeq 2×10^9$)
Javaでの解答例
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int a[] = new int[n];
for (int i = 0; i < n; i++){
int A = scan.nextInt();
a[i] = A;
}
long ans = 0;
for (int i = 1; i < n; i++){
if (a[i-1] > a[i]){
ans = ans + (a[i-1]-a[i]);
a[i] = a[i-1];
}
}
System.out.println(ans);
}
}
ansの値が$2×10^9$を超える可能性があるので、ansの型はlongにしましょう。
(∵ $2^{31}-1 \simeq 2×10^9$)
以上、ABC 176 C問題「Step」の解説でした。
記事を読んで分からない点等ありましたらコメントをよろしくお願いします!!