共役勾配法を可視化してみた

この記事は1年以上前にアップする予定だったのですが、バグがあったため放置しており、ようやくアップできました。

前回「これなら分かる最適化数学」という本の「勾配法」を可視化してみたので、次は同じ本の「共役勾配法」を可視化してみました。

5本のプログラムは関数部分以外は全く同じなので、2本目からは関数部分のみを掲載しました。

間違いなどありましたら、指摘していただけるとありがたいです。

参考にさせていただいたサイト

• 共役勾配法 – 共役勾配な方向って何だろう
• 共役勾配法 – アルゴリズムと実際の計算

参考にさせていただいた本

• これなら分かる最適化数学　基礎原理から計算手法まで

参考にさせていただいたグラフ表示に関するサイト（実際に参考にしたのは「Visual C++の易しい使い方（23） ―三次元グラフの陰線処理―」の方ですが、今は公開されていないようです）

• 隠線処理を用いた三次元グラフの作成

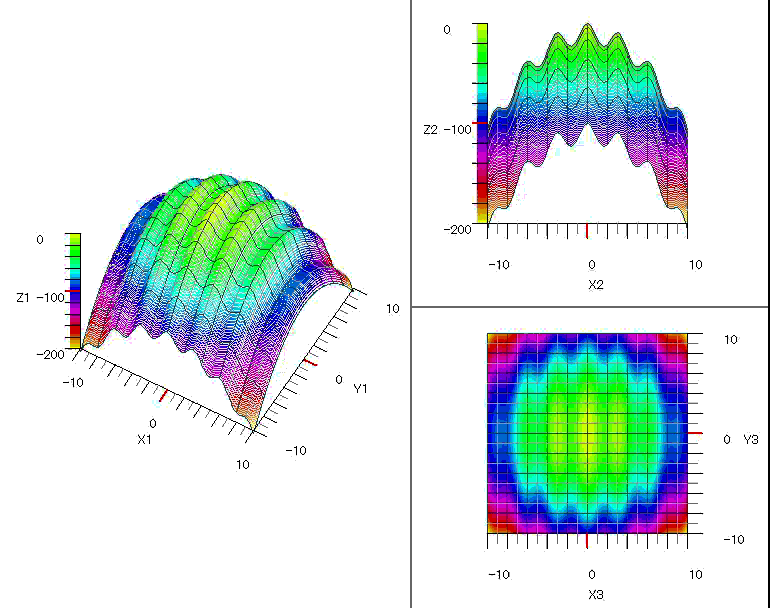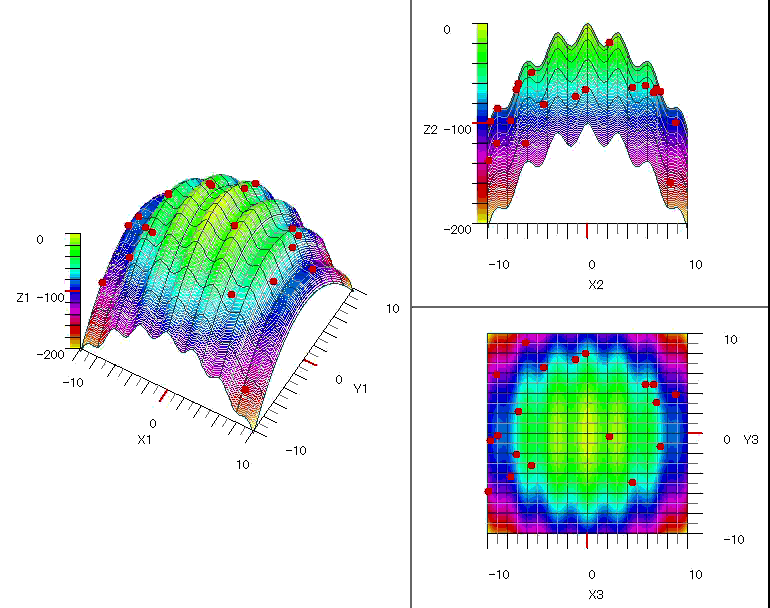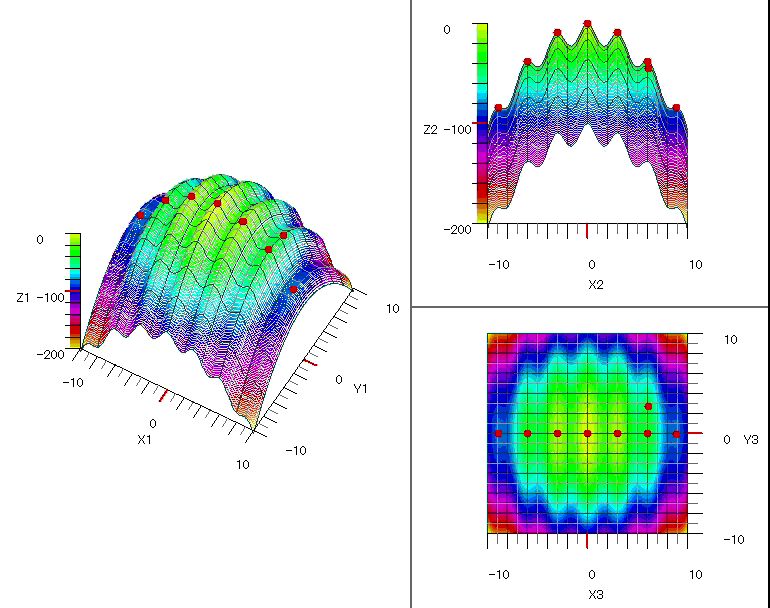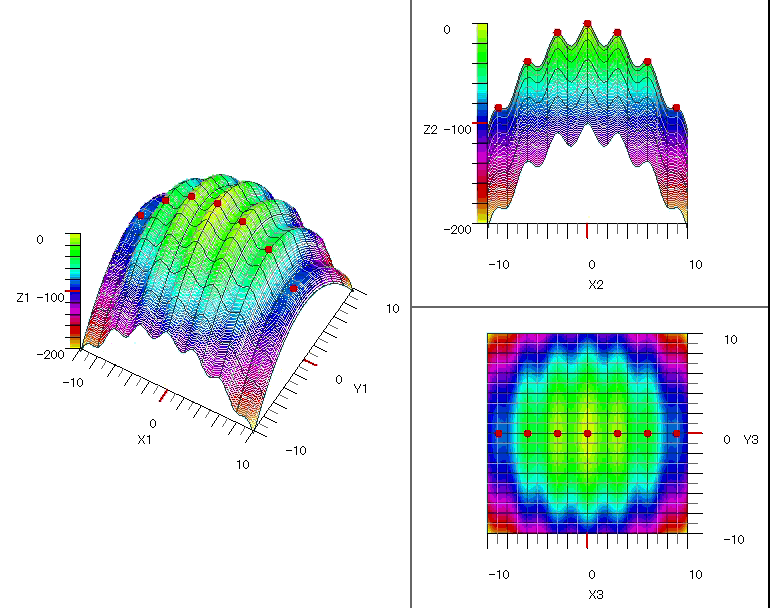
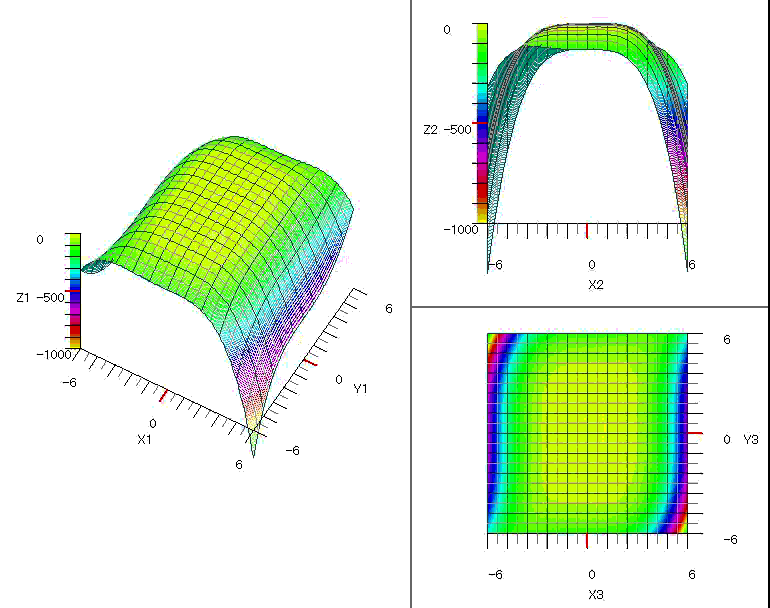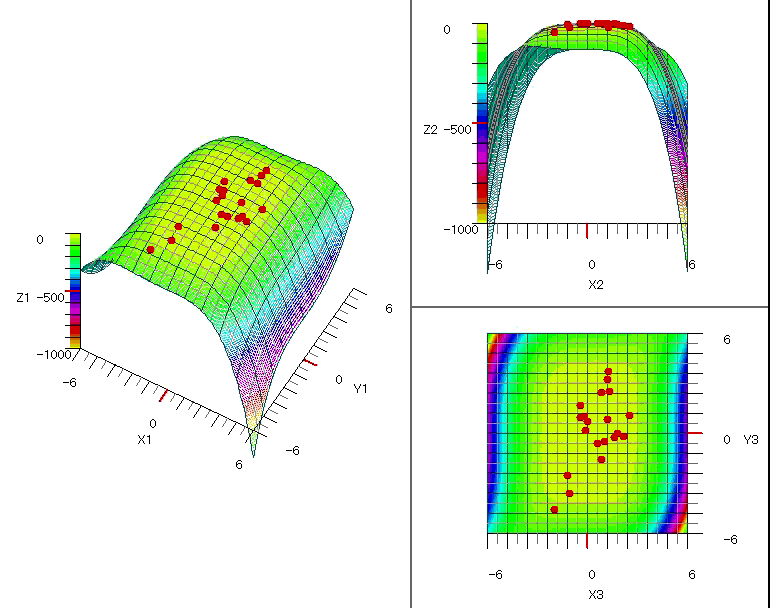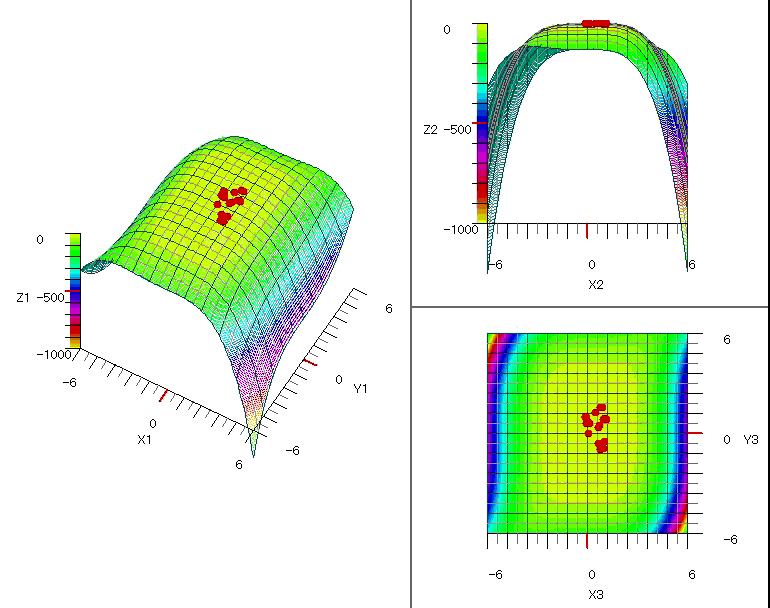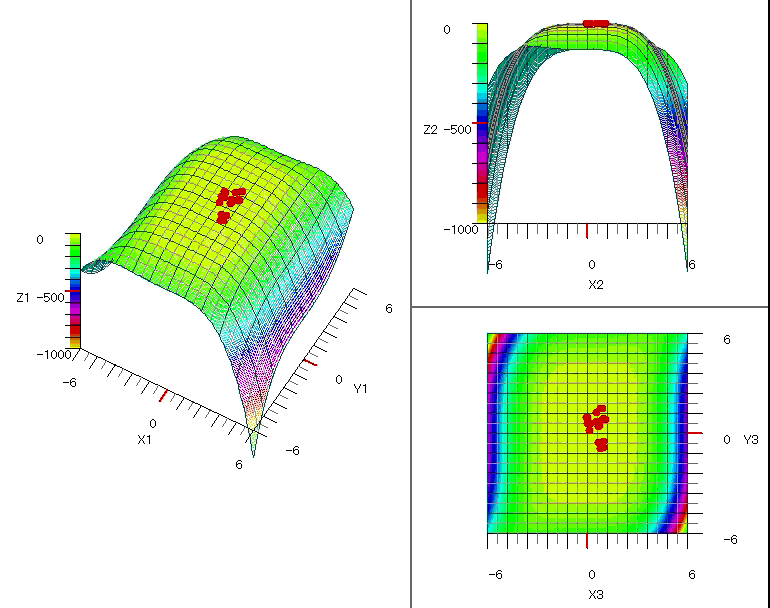
図1～図5に各関数の探索の様子をグラフに表示しました。

図1 $\quad-5(x-1)^2-2(y-2)^2$

図2 $\quad-x^2-y^2-20\sin^2 x$

図3 $\quad-x^3-y^3+9xy-27$

図4 $\quad-0.5x^4-0.1y^4+0.01x^3y^3+x+0.3y$

図5 $\quad-x^2+xy-y^2+x+y$

ConjugateGradient1.cpp

#define _USE_MATH_DEFINES
#include <math.h>
#include <iostream>
#include <fstream>

#include <cmath>
#include <iomanip>
#include <vector>

using namespace std;

// 0以上1以下の実数乱数
#define RAND_01 ((double)rand() / RAND_MAX)

const int ITERATION = 10; // 試行回数
const int SWARM_SIZE = 20; // 群の大きさ

double X_MAX = 10; // graphのX軸の表示範囲の上限
double X_MIN = -10; // graphのX軸の表示範囲の下限

double Y_MAX = 10; // graphのY軸の表示範囲の上限
double Y_MIN = -10; // graphのY軸の表示範囲の下限

double Z_MAX = 0;
double Z_MIN = -200;

string str_formula = "-1.0 * (x**2 + y**2)";

double x[ITERATION][SWARM_SIZE];
double y[ITERATION][SWARM_SIZE];
double z[ITERATION][SWARM_SIZE];

// 共役勾配法で計算する関数定義
double function(double x, double y)
{
	double z;

	z = -5 * (x - 1) * (x - 1) - 2 * (y - 2) * (y - 2);

	return z;
}

void set_function_conditions()
{
	X_MAX = 4;
	X_MIN = -6;
	Y_MAX = 4;
	Y_MIN = -6;
	Z_MAX = 0;
	Z_MIN = -400;
	str_formula = "-5 * (x - 1)**2 - 2 * (y - 2)**2";
}

// 1変数の勾配法

// 関数 F(t) の定義
// F = lambda t : self.func(x[0] + t * m[0], x[1] + t * m[1])
double func1(double x1, double y1, double t, int j, double m[][2])
{
	double x2 = x1 + t * m[j][0];
	double y2 = y1 + t * m[j][1];
	double f = function(x2, y2);
	return f;
}

double diff_func(double x1, double y1, double t, int j, double m[][2])
{
	double delta_h = 0.000001;
	double f1 = func1(x1, y1, t + delta_h, j, m);
	double f2 = func1(x1, y1, t - delta_h, j, m);
	double f3 = (f1 - f2) / (2.0 * delta_h);
	return f3;
}

double get_sign(double s)
{
	if (s > 0.0)
		return 1.0;
	else if (s < 0.0)
		return -1.0;
	else
		return 0.0;
//	if (s >= 0.0)
//		return 1.0;
//	else
//		return -1.0;
}

double search_max(double x1, double y1, double initial_t, double initial_h, double epsiron, int j, double m[][2])
{
	// step 1 : 初期値の設定
	double t = initial_t;
	double h = initial_h;
	
	// 収束のチェック
	while (fabs(diff_func(x1, y1, t, j, m)) > epsiron) {
		// step 2
		h = get_sign(diff_func(x1, y1, t, j, m)) * fabs(h);
		cout << "h1 = " << h << endl;
		double T = t;
		double Td = t + h;

		double fT = func1(x1, y1, T, j, m);
		double f2 = func1(x1, y1, Td, j, m);
		cout << "fT = " << fT << " f2 = " << f2 << endl;
//		if (fT < func1(x1, y1, Td, j, m)) {
		if (fT < f2) {
			while (fT <= func1(x1, y1, Td, j, m)) {
				h = 2.0 * h;
				T = Td;
				Td = T + h;

				fT = func1(x1, y1, T, j, m);
				if (fT > Z_MAX)
					break;
			}
			// step 3 (b)
			t = T;
			h = h / 2.0;
			if (j == 0)
				cout << "t1 = " << t << "  h1 = " << h << endl;
			
		//else: # step 4
		} else {
			while (fT >= func1(x1, y1, Td, j, m)) {
				h = h / 2.0;
				Td = Td - h;

				fT = func1(x1, y1, T, j, m);
				if ((fT > Z_MAX) || (h == 0.0))
					break;
			}
			// step 4 (b)
			t = Td;
			h = 2.0 * h;
			if (j == 0)
				cout << "t2 = " << t << "  h2 = " << h << endl;
		}
		if ((fT > Z_MAX) || (h == 0.0))
			break;
	}
	
	return t;
}

// 共役勾配法 2変数を扱う

double __delta_h = 0.0001;

double dfdx(double x1, double y1)
{
	double f1 = function(x1 + __delta_h, y1);
	double f2 = function(x1 - __delta_h, y1);
	double f3 = (f1 - f2) / (2.0 * __delta_h);
	return f3;
}

double dfdy(double x1, double y1)
{
	double f1 = function(x1, y1 + __delta_h);
	double f2 = function(x1, y1 - __delta_h);
	double f3 = (f1 - f2) / (2.0 * __delta_h);
	return f3;
}

double ddfdxdx(double x1, double y1)
{
	double f1 = dfdx(x1 + __delta_h, y1);
	double f2 = dfdx(x1 - __delta_h, y1);
	double f3 = (f1 - f2) / (2.0 * __delta_h);
	return f3;
}

double ddfdxdy(double x1, double y1)
{
	double f1 = dfdx(x1, y1 + __delta_h);
	double f2 = dfdx(x1, y1 - __delta_h);
	double f3 = (f1 - f2) / (2.0 * __delta_h);
	return f3;
}

double ddfdydx(double x1, double y1)
{
	double f1 = dfdy(x1 + __delta_h, y1);
	double f2 = dfdy(x1 - __delta_h, y1);
	double f3 = (f1 - f2) / (2.0 * __delta_h);
	return f3;
}

double ddfdydy(double x1, double y1)
{
	double f1 = dfdy(x1, y1 + __delta_h);
	double f2 = dfdy(x1, y1 - __delta_h);
	double f3 = (f1 - f2) / (2.0 * __delta_h);
	return f3;
}

// 勾配の計算
void calc_gradient(double gradient[][2], double x1, double y1, int j)
{
	gradient[j][0] = dfdx(x1, y1);
	gradient[j][1] = dfdy(x1, y1);
}

// ヘッセ行列の計算
void calc_hessian(double hessian[][2], double x1, double y1)
{
	hessian[0][0] = ddfdxdx(x1, y1);
	hessian[0][1] = ddfdxdy(x1, y1);
	hessian[1][0] = ddfdydx(x1, y1);
	hessian[1][1] = ddfdydy(x1, y1);
}

//  2次形式の内積計算
double calc_inner(double a[][2], double H[][2], double b[][2], int j)
{
	double r_v[2];
	r_v[0] = H[0][0] * b[j][0] + H[0][1] * b[j][1];
	r_v[1] = H[1][0] * b[j][0] + H[1][1] * b[j][1];
	double inner = a[j][0] * r_v[0] + a[j][1] * r_v[1];
	return inner;
}

void conjugate_gradient()
{
	// 収束判定の定義
	double delta = 0.001;


	// 初期値の設定
	double alpha[SWARM_SIZE];
	double m[SWARM_SIZE][2];
	for (int j = 0; j < SWARM_SIZE; j++) {
		alpha[j] = 0.0;
		m[j][0] = 0.0;
		m[j][1] = 0.0;
	}

	for (int i = 1; i < ITERATION; i++) {
		for (int j = 0; j < SWARM_SIZE; j++) {
			double x1 = x[i-1][j];
			double y1 = y[i-1][j];

			// 共役勾配な方向を計算
			double gradient[SWARM_SIZE][2];
			calc_gradient(gradient, x1, y1, j);
			m[j][0] = gradient[j][0] + alpha[j] * m[j][0];
			m[j][1] = gradient[j][1] + alpha[j] * m[j][1];
			if (j == 0) {
				cout << "m[0][0] = " << m[0][0] << endl;
				cout << "m[0][1] = " << m[0][1] << endl;
			}

			// 最大値 t の探索の初期設定
			double initial_t = 0.01; // 初期値は常に0.01から始める
			double initial_h = 0.01;
			double epsiron = 0.0001; // 収束判定
			
			// 勾配法で最大値 tを探索する
			double max_t = search_max(x1, y1, initial_t, initial_h, epsiron, j, m);

			//　解の方向
			x1 = x1 + max_t * m[j][0];
			if (x1 > X_MAX)
				x1 = X_MAX;
			else if (x1 < X_MIN)
				x1 = X_MIN;

			y1 = y1 + max_t * m[j][1];
			if (y1 > Y_MAX)
				y1 = Y_MAX;
			else if (y1 < Y_MIN)
				y1 = Y_MIN;

			x[i][j] = x1;
			y[i][j] = y1;
			z[i][j] = function(x1, y1);

			// alphaの更新
			double hessian[2][2];
			calc_hessian(hessian, x1, y1);
			calc_gradient(gradient, x1, y1, j);
			double numerator = calc_inner(m, hessian, gradient, j);
			double denominator = calc_inner(m, hessian, m, j);
			
			alpha[j] = - numerator / denominator;

			if (j == 0) {
				cout << "i = " << i << endl;
				cout << "max_t = " << max_t << endl;
				cout << "x1 = " << x1 << " y1 = " << y1 << endl;
				cout << "gradient = " << gradient[0][0] << " " << gradient[0][1] << endl;
				cout << "hessian = " << hessian[0][0] << " " << hessian[0][1] << " " << hessian[1][0] << " " << hessian[1][1] << endl;
				cout << "numerator = " << numerator << endl;
				cout << "denominator = " << denominator << endl;
			}

			// 収束条件の判断
//			double d = sqrt(pow(max_t * m[0], 2) + pow(max_t * m[1], 2));
			
//			if (d < delta)
//				break;

//			if (isnan(x[0]))
//				break;
		}
	}
}

void initialize()
{
	for (int i = 0; i < SWARM_SIZE; i++) {
		x[0][i] = RAND_01 * (X_MAX - X_MIN) + X_MIN;
		y[0][i] = RAND_01 * (Y_MAX - Y_MIN) + Y_MIN;
//		x[0][i] = -3.0;
//		y[0][i] = -6.5;
		z[0][i] = function(x[0][i], y[0][i]);
	}
}

void write_data();

int main()
{
	srand ((unsigned)time(NULL));

	set_function_conditions();

	initialize();

	// 共役勾配法の実行
	conjugate_gradient();

	// 結果表示
	write_data();
}

void write_data()
{
	ofstream fout;
	fout.open("graph_data.txt");

	fout << str_formula << endl;
	cout << str_formula << endl ;

	fout << "ITERATION " << ITERATION << endl;
	cout << "ITERATION " << ITERATION << endl;

	fout << "SWARM_SIZE " << SWARM_SIZE << endl;
	cout << "SWARM_SIZE " << SWARM_SIZE << endl;

	fout << "X_MAX " << X_MAX << endl;
	cout << "X_MAX " << X_MAX << endl;

	fout << "X_MIN " << X_MIN << endl;
	cout << "X_MIN " << X_MIN << endl;

	fout << "Y_MAX " << Y_MAX << endl;
	cout << "Y_MAX " << Y_MAX << endl;

	fout << "Y_MIN " << Y_MIN << endl;
	cout << "Y_MIN " << Y_MIN << endl;

	fout << "Z_MAX " << Z_MAX << endl;
	cout << "Z_MAX " << Z_MAX << endl;

	fout << "Z_MIN " << Z_MIN << endl;
	cout << "Z_MIN " << Z_MIN << endl;

	fout << "DATA" << endl;
	cout << "DATA" << endl;

	for (int i = 0; i < ITERATION; i++) {
		cout << i << endl;
		for (int j = 0; j < SWARM_SIZE; j++) {
			cout << x[i][j] << " " << y[i][j] << " " << z[i][j] << endl;
			fout << x[i][j] << " " << y[i][j] << " " << z[i][j] << endl;
		}
		cout << endl;
		fout << endl;
	}

	fout.close();
}

ConjugateGradient2.cpp

double function(double x, double y)
{
	double z;

	z = x * x + y * y + 20.0 * sin(x) * sin(x);

	return z;
}

void set_function_conditions()
{
	X_MAX = 10;
	X_MIN = -10;
	Y_MAX = 10;
	Y_MIN = -10;
	Z_MAX = 200;
	Z_MIN = 0;
	str_formula = "x**2 + y**2 + 20.0 * sin(x)**2";
}

ConjugateGradient3.cpp

double function(double x, double y)
{
	double z;

	z = -1.0 * (x * x * x + y * y * y - 9.0 * x * y + 27.0);

	return z;
}

void set_function_conditions()
{
	X_MAX = 10;
	X_MIN = -10;
	Y_MAX = 10;
	Y_MIN = -10;
	Z_MAX = 3000;
	Z_MIN = -1500;
	str_formula = "-1.0 * (x**3 + y**3 - 9.0 * x * y + 27.0)";
}

ConjugateGradient4.cpp

double function(double x, double y)
{
	double z;

	z = -0.5 * x * x * x * x - 0.1 * y * y * y * y + 0.01 * x * x * x * y * y * y + x + 0.3 * y;

	return z;
}

void set_function_conditions()
{
	X_MAX = 6;
	X_MIN = -6;
	Y_MAX = 6;
	Y_MIN = -6;
	Z_MAX = 0;
	Z_MIN = -1000;
	str_formula = "-0.5 * x**4 - 0.1 * y**4 + 0.01 * x**3 * y**3 + x + 0.3 * y";
}

ConjugateGradient5.cpp

double function(double x, double y)
{
	double z;

	z = -x * x + x * y - y * y + x + y;

	return z;
}

void set_function_conditions()
{
	X_MAX = 10;
	X_MIN = -10;
	Y_MAX = 10;
	Y_MIN = -10;
	Z_MAX = 0;
	Z_MIN = -300;
	str_formula = "-x**2 + x * y - y**2 + x + y";
}