しっかり問題は読んで理解しよう！
難しい問題文に出会ってもすぐに諦めないで！
#AGC043A
Difficulty:803
強敵！
でも以下のポイント2つをクリアすればこの問題はとける！
①問題読解力
②DP(動的計画法)
##①問題読解力
問題文の後半の「以下の操作」が頭に全く入ってこなかった！
ここでは「以下の操作」の解読をしていきます。
「以下の操作」の部分を問題より引用
4つの整数r0,c0,r1,c1(1≤r0≤r1≤H,1≤c0≤c1≤W)を選ぶ。
r0≤r≤r1,c0≤c≤c1を満たす全てr,cについて、(r,c)の色を変更する。つまり、白色ならば黒色にし、黒色ならば白色にする。
？？？
諦めないで！
とりあえず具体例を考えよう！
ノートとペンを用意！
※競プロにノートとペンは必須です！
【Python】ABC159D(高校数学nCr)【AtCoder】より
たとえば4*4のこんな図形だったとしましょう。
とりあえず黒色と白色を塗ります。
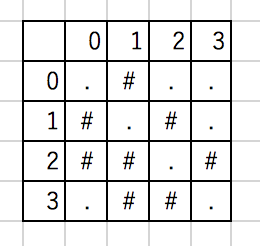
左上(0,0)がスタート、右下(3,3)がゴール。
途中経路として右か下しかいけません！
白が道。黒が障害物みたいな感じ。
今(0,0)から右に行こうか左に行こうか迷ってます！
ここで「以下の操作」の登場！
4つの整数r0,c0,r1,c1(1≤r0≤r1≤H,1≤c0≤c1≤W)を選ぶ。
r0,c0,r1,c1(rは行、cは列)は上記の条件で好きに(任意に)選んでいいみたいなので、
r0,c0,r1,c1 = 1,0,3,2
※r,cは1以上(問題文では左上(1,1)スタート)となってますが、俺の画像はインデックスの関係で左上(0,0)スタートなので注意。
としてみると・・・
r0≤r≤r1,c0≤c≤c1を満たす全てr,cについて、(r,c)の色を変更する。つまり、白色ならば黒色にし、黒色ならば白色にする。
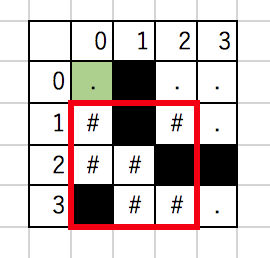色が変わったよ！
これで「操作」は1回！
すると、なんともう操作をせずに右下まで行けちゃうルートができてる！
なのでこの問題の答えは「1」回が正解となります。
ここからわかることは、黒色(障害物みたいなもの)が繋がってたら、1回の「操作」で白色(道)に変えられる！
ということです！
ここ理解できれば、あとはプログラムを実装するだけになります！
おまけで雑談ですが、
コンテスト本番で、問題を早く正確に理解(解読)できるようにするためには
問題読解力をあげていくことが必要です。
問題読解力の上げ方は以下の2つだと個人的に思っています。
- A:日本語の難しい問題を多くこなす（似たパターンが解けるようになる）
- B:日本語の難しい問題に出会った時に、すぐに解説を見ずに(逃げずに)ノートとペンを使って考える癖をつける(実戦でしか身につかない)
##②DP(動的計画法)
①が長かったですが、
①の内容を理解した上で②はDPの基本中の基本さえ理解できていれば、この問題は解けるはず！
※「DPの基本中の基本」の俺の中の基準は以下のかえるくん問題2問が解けるかどうか
考え方的には、
- 1行目と1列目は別で考える(俺の中ではdpmapの初期値を設定しているイメージ)
- 2行目・2列目以降は上からきたパターンと左から来たパターンのそれぞれの操作回数の小さい方を2次元配列のdpmapに入れていく感じ
- 最終的な答えはdpmapの右下(dpmap[-1][-1])
##①+②
まとめると、こんな感じになるかな〜。
def LI(): return list(map(int,input().split()))
H,W = LI()
S = [input() for _ in range(H)]
dp = [[-1]*W for _ in range(H)]
for i in range(H):
for j in range(W):
judge = 1 if S[i][j]=='#' else 0
if i==0: #0行目
if j==0:
dp[0][0] = judge
else:
dp[0][j] = dp[0][j-1]+judge*(0 if S[0][j-1]=='#' else 1)
else: #0行目以外
if j==0:
dp[i][0] = dp[i-1][0]+judge*(0 if S[i-1][0]=='#' else 1)
else:
temp1 = dp[i][j-1]+judge*(0 if S[i][j-1]=='#' else 1)
temp2 = dp[i-1][j]+judge*(0 if S[i-1][j]=='#' else 1)
dp[i][j] = min(temp1,temp2)
print(dp[-1][-1])
この問題はアルゴリズム自体の難易度はそれほど高くない(2次元配列にしているくらいでDPの基本レベル)のに、
問題文が難しくてDifficultyがはねあがってる。
逆に言うと、問題読解力をあげる事ができればレート一気にあがりそう！！！
がんばろ！
おわり！