(はじめに)
本記事は、ディジタル信号処理の FIR フィルタを FPGA 等のカスタムのディジタル回路で実現する場合に用いられる "Super Sample Rate" について、 "Poly Phase 分解" と比べながら簡単な説明を試みるものです。
少し前の記事のフォロー記事の反響で「Super Sample Rate って初めて聞きました、Poly Phase 分解 のことでしょうか」、というご意見を頂きました。
Super Sample Rate は Poly Phase 分解の裏返しみたいな概念です。
と返答しましたが、絵がないとちょっとわかりづらいかもしれないので、作って色々考えてみた、という記事です。(経験者には"あたりまえ"で物足りないかもしれませんが基本のおさらいとしてご覧ください)
"Super Sample Rate" で google 検索すると、私の記事が筆頭ヒットするぐらい、使われていない用語ですが、Intel と Xilinx の信号処理(DSP)向け IP/solution 関係で使われている用語で、どちらかのメーカーが言い出したと推測しています。(または関係の近い論文が初出?)
(Super Sample Rate とは?)
簡単な定義は「サンプルレートがクロックレートより高い場合」です。
より典型的な場合で説明すると、クロックレートよりも高いサンプリング周波数のサンプルデータ系列が、データを並列に並べて転送する「マルチレーン伝送」で転送されて来た場合、かつそれを FIR フィルタなどの信号処理演算を行う場合に、伝送や処理を指して "Super Sample Rate" という、と考えて良さそうです。
その方法で、クロックよりも高いサンプルレートに仮想的/等価的に対応・実現できている、ということになります。
Intel と Xilinx の FIR フィルタ IP の資料で下記の様に説明しています。
Intel FIR II IP Core User Guide (v17.1/2020.06.12)
For a “super sample rate” filter the sample rate is greater than the clock rate.
Xilinx FIR Compiler v7.2 IP Product Guide (January 21, 2021)
When the required sample frequency is greater than the clock frequency, the core accepts multiple parallel samples every clock cycle for each data channel.
(背景)
高速通信(例 5G wireless や 100GbE) ではコストなどの理由で、額面のレートをそのまま1本で伝送せずにレートを落とし、複数本で並列化して伝送する場合が多くあります。
通信としてはマルチレーン伝送 (Multi Lane Distribution; MLD) と呼ばれる様です。
Wireless 通信等では AD/DA Converter の性能向上で直接 RF 帯域の信号をデジタル化して扱う Direct RF サンプリングが行われる様になってきています。
コストが許せば FPGA 等を使って、FIR フィルタ処理をこの帯域で行うことも考えられます。本記事ではその様に RF 帯域のサンプリング系列に直接 FIR フィルタ処理を行うシチュエーションとします。
なお、通信では物理層の1クロックで1レーンまたはチャンネルに何ビットの情報が乗っているかは、方式次第ですが 1bit という場合もあります。
一方 FIR フィルタにかけるようなサンプルデータは、扱う数値のデータ型(ex. 16bit固定小数点数、単精度浮動小数点数)のビット数が1クロックでパラレルにまとまって計算されるという扱いが通常は行われます。(HDL 記述やそれ以上の設計レベル)
本記事では後者の扱いでこれらのギャップの詳細には触れないものとします。1レーン、1チャンネルには1クロックで1サンプルデータが乗っている前提での話です。
(転送と FIR 処理の対比図)
本記事の主題がこの図です。上段が転送(伝送)のイメージ、下段が対応する FIR フィルタのイメージです。(盛り込んだ図ですので別途拡大しながらでも読んでください)
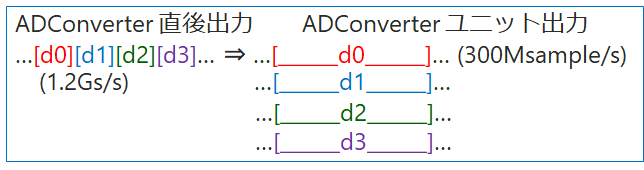
サンプルデータの赤い枠は 1.2GHz 、黒い枠は 300MHz、緑の枠は 75MHz の1サイクルのデータです。データレートの基本単位 T/s = Transfer per sec はそのまま FIR フィルタ回路の計算速度(スループット)になりますので分けて書いていません。
E 列が通常の 300MHz でサンプルデータが到来して 300MHz で直接型の FIR フィルタを動かしているイメージになります。データ系列のイメージそのままのシフトレジスタのデータが下段の積和演算回路にそのまま入力されて結果が得られるとします。(適切にパイプライン化)
B 列が 4倍速い 1.2GHz、H 列が 1/4 の 75MHz のレートで動かした場合ですが、当然 B 列の方は実際に作るには色々大変になります。
そこで、マルチレーン伝送で対応し、FIR フィルタの方もそのまま対応できるのが C 列の Super Sample Rate 方式、という事になります。
一方、H 列のほうは低コストデバイスや低消費電力向けではこのまま作ることも考えられますが、FPGA が 300MHz で動かせる状況ではフィルタ回路の積和演算回路がチップ面積上少々もったいないので、G 列の様に、ポリフェーズ分解して演算リソースを使いまわし式に節約することが行われます。
D 列はチャンネル独立のまま4並列化した場合、F 列はこれも時間を4つに分割して独立の4チャンネルのデータを持たせた通常の TDM の場合です。
E 列を中心に対称的に見えて微妙に食い違っています。
あえて一言でまとめますと「時間と空間をトレードオフした場合対称的にならない」ということでしょうか??(前提条件が曖昧とか飛躍しすぎとかご指摘あるかもしれませんが)
D 列と F 列のデータ転送のイメージが対称的(裏返し)の関係にはみえますが、物理的な空間(並列、レーン)と時間上の位置を交換(パラレル・シリアル間の変換)する場合にセレクタが必要になるというところで微妙な非対称性を感じます。
Super Sample Rate と Poly Phase Decomposition はさらにそれぞれの変形があって非対称的です。
Super Sample Rate (C 列)はチャンネル(レーン)並列(D 列)の特殊な場合で論理的にチャンネルを1つにまとめて B 列と同様の扱いをする場合になります。
Poly Phase Decomposition (G 列)は時分割多重化(F 列)のデータ有効(valid)制御を調整して転送効率をわざと下げた場合になり、これだけが転送 i/f の利用効率が 1/4 になっています。転送効率の低下によってできた空き時間を利用して、リソースは利用効率は下げずに量を 1/4 に減らした形です。(アキュムレータ(Acc.) などのオーバーヘッドが必要ですが)フィルタ係数(積和演算)を4組に分解して、計算を時分割で順に間に合う様に行っていく形です。
なお、これは Poly Phase 分解の実装の1つの方法で、リソース量をそのままにして動作レートのほうを 1/4 に下げる実装もあります。その場合、分解された各部がそのまま並列に存在するので C 列の構成に近い面もありますが、C 列の方は各レーンでフィルタ係数がフルセットになっていることがやはり異なる点になります。(分解せずそのまま並列・倍化)
(Parallel FIR filter が Super Sample Rate に相当する場合)
"Parallel FIR filter" で google 検索すると、上の図の D 列の様なチャンネル間は無関係でただ単に FIR フィルタを並べただけ、というものではなく、入出力については本記事の Super Sample Rate 相当のものが引っかかってきます。
例えばある US Patent では、サンプルレートをクロックより高くすることが目的ではない為か、入出力が Super Sample Rate 構成になっていますが取り立ててその事は主張はされていません。
その US Patent では、Poly Phase 分解を低レートの並列フィルタへの分割として捉えています。分解した後のサブフィルタの構成を変形することでリソース量を削減することが「発明の効果」の様です。(上の図の G 列の様な時分割処理にはしていない)
上記以外には直接形(Direct Form)ではなく転置形(Transposed Form)にして元記事の様に組み合わせ回路部分を多段に重ねた様なものもあります。元記事の見方だとそれは加算回路の遅延が累積するので "Super Sample Rate" 実現には有利ではないのですが、データレートが低くてリソースを節約したり、乗算器を使わない様に多段の加算器に分散したり(Distributed Arithmetic)する場合には都合が良い様です。
余談ですが、何が最適かはやはり要求仕様や使用デバイスによって全く異なると改めて気づかされる次第です。
(おわりに)
"Super Sample Rate" について、"Poly Phase 分解" との違いを図にして説明を試みてみました。
直列と並列の変換=時間と空間のトレードオフ で微妙に対称的ではない関係を示しました。
同様な回路を設計される場合の参考になれば幸いです。
(文中に記載されている会社名、商品名は各社の商標または、登録商標です。)