(はじめに)
5G など超高速通信で使うような GHz クロックでサンプル(GSPS)する高速 AD Converter の出力を、FPGA のロジックなど通常のディジタル回路で受け取る場合、クロックレートを落として並列にしてサンプルデータを受け取ることが行われます。
その様な対応を Super Sample Rate と呼ぶことがあります。
受け取ったサンプルデータにそのまま FIR フィルタなどの計算を行いたい場合、クロックを上げるわけにはいかないのでやはり並列処理でうまく処理する必要があります。
データの index 計算が面倒に感じたので、なにかうまい方法がないかと考えた結果、ちょっと原点回帰してみて、Mealy Machine を変形する形で作ってみました。
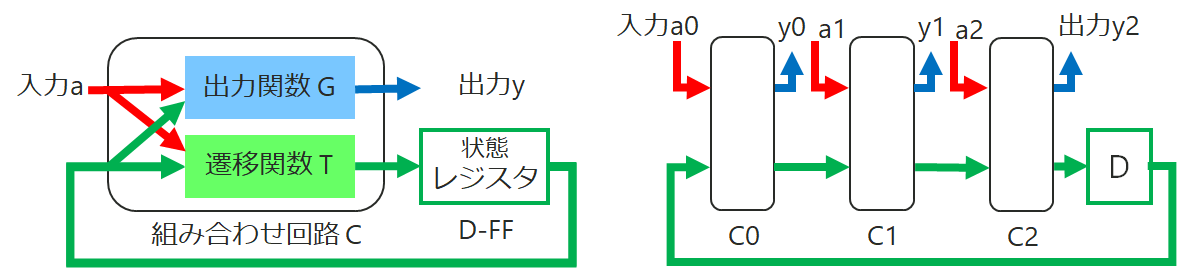
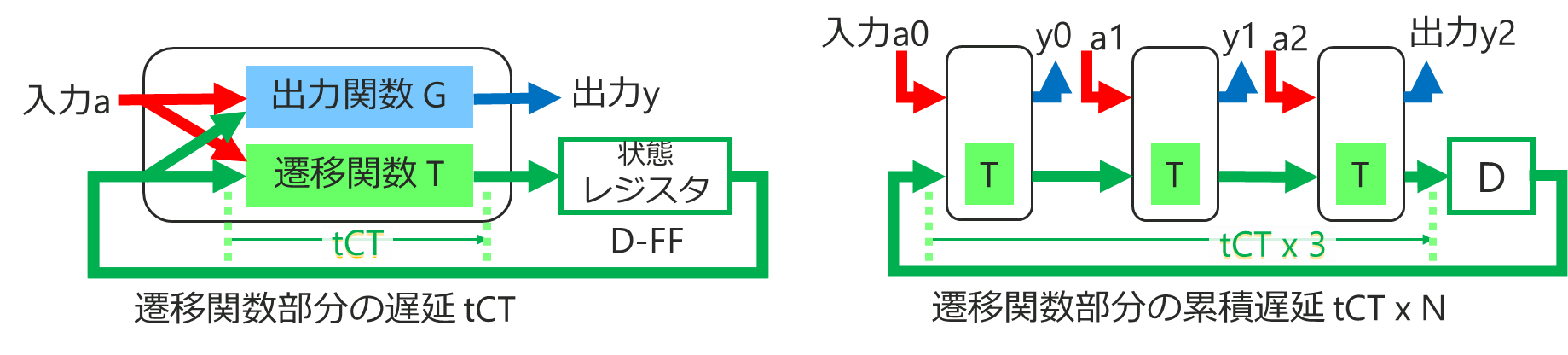
左の図が Mealy Machine のブロック図表現で、一般的なクロック同期のディジタル回路は全てこれで表現できます。(有限状態機械 Finite State Machine (FSM) とも言います。)
これを右の図の様に組み合わせ回路部分を3段一度に計算する様に変形すると、1クロックで元の3クロック分の計算をこなす”3倍速い”回路が作れるかも、というアイデアです。
実際にこの構造の**モデルベース設計(MBD)**を作ってみて動作は確認できました。
Verilog RTL など HDL でも同様に書けると思います。
(HDL 版は未完成ですので、一部載せるだけにしています。)
モデルベースの設計内容は後半で説明します。本記事では考え方の説明が中心になります。
(背景)
筆者はデジタル回路の設計を Verilog HDL 記述や、”DSP Builder for Intel® FPGA”(以下 DSP Builder) を使って行っています。
DSP Builder はややマイナーかもしれませんが、Mathworks® 社の HDL Coder™ の Intel FPGA 専用版に相当すると考えてよく、 Simulink モデルの形でモデルベース設計(Model Base Design; MBD)を行うことができます。
冒頭で触れましたように、最近 Super Sample Rate のサンプルデータ系列を処理するにはどうすれば良いか考える機会がありました。Super Sample Rate のイメージですが、例えば1.2Gs/sec のサンプリング系列を 300Ms/sec 4 レーンに分けた場合、下図の様になります。
Intel 社の資料だと FIR II IP のユーザーガイドにこんな図があります
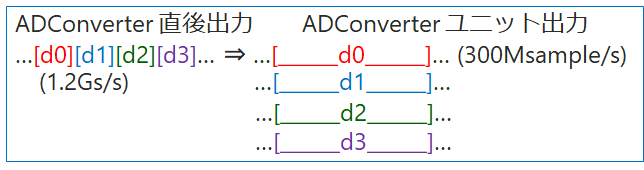
この様に並列にシステムクロックの N(=4) 倍のサンプリングデータを転送する場合、”Super Sample Rate” と Intel などの資料では呼んでいます。あまり広く使われていない用語なのか、ADC 側の資料では不思議と見かけません。
なお、画像処理分野で “Super Sampling” がアンチエイリアス技術の一手法として有名で、他に Audio や AI (Deep Learning)分野で “Super Sampling” という用語が使われている様ですが、この記事は、直接には画像処理・Audio・AI 分野の “Super Sampling” とは関係ありません。
(これら向けの設計に本記事の表現が使える可能性も否定はしませんが。)
(課題:Super Sample Rate を処理する回路は表現しにくそう?)
受け取り側で FIR filter 等、ある長さの連続サンプリングデータに対して処理を行う場合、Super Sample Rate の場合はどのように計算(表現)すれば良いか?という疑問がありました。正直に考えてみた例が下記です。
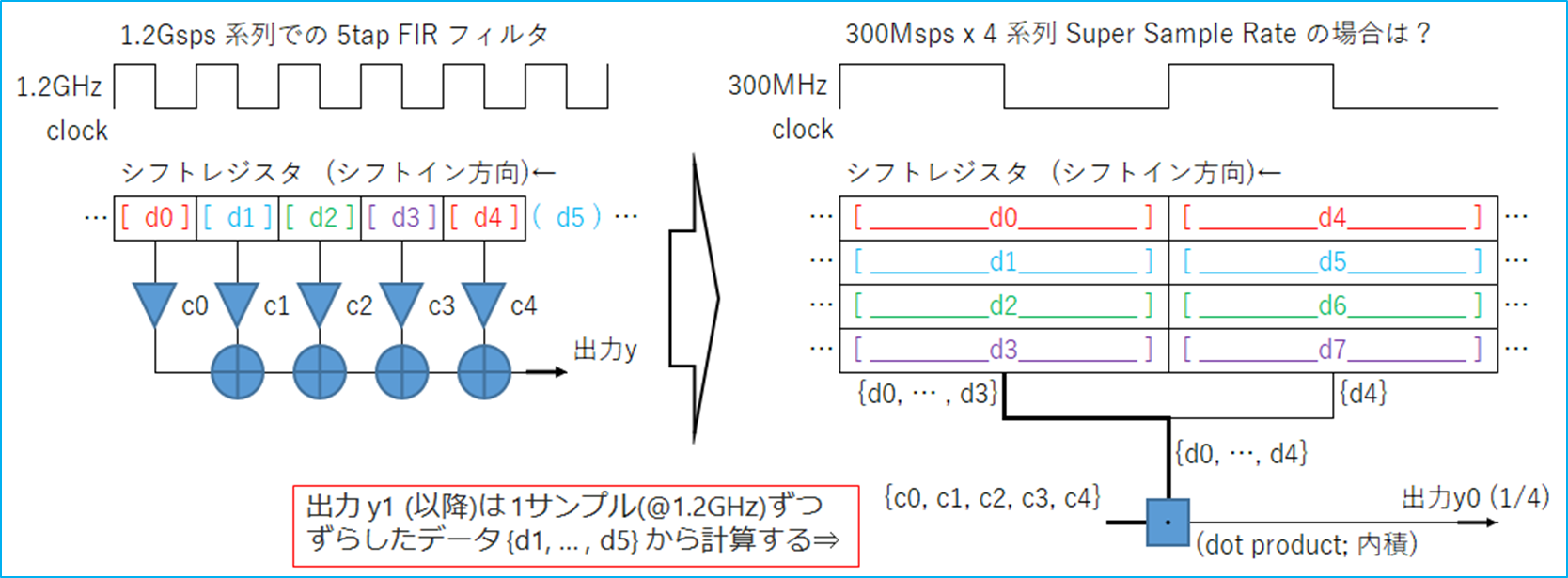
1.2Gsps/Hz で作れるなら、オーソドックスな構成で各クロック動かせば済む回路が、Super Sample Rate では先頭と末尾は4レーンの一部を取り出して、計算しないといけない場合があるので、ちょっと面倒になってきます。
作れなくはないが、N=4 を変更する場合なにか間違ってしまいそうです。そこは頑張って、少々複雑でも、データ選択の index 計算をちゃんと作り、並列度 N の変更にも対応するものを用意すれば済むだけかもしれませんが、個人的にちょっと嫌気がさしました...
発想:Mealy Machine 多段化表現
そこで冒頭でも述べたように、Mealy Machine を N 段カスケードに並べた回路で Super Sample Rate の処理を表現すれば、N を変更しても紛らわしくないという発想に至りました。

ちょっと縦方向を縮めていますが冒頭の Mealy Machine の組み合わせ回路3段化の図です。本記事の核心は言ってみればこの図に尽きますが、これを元にあれこれ考察してみました。
(以後、似た様な図が続くので説明は読みやすいように箇条書き中心にしました)
- 元の回路(左)は1クロックで1サンプル処理
- Super Sample Rate では N サンプルを N 段で 1 クロックで処理(右、図は N=3 の場合)
- 状態レジスタ D-FF は元の構成の N サイクル毎の状態のみを、毎クロック保持・遷移
- 途中の状態は、組み合わせ回路のステージ間に現れるが、状態としては保持せずスキップ
これで N をどんどん増やせばハードウェア量の許す限りディジタル回路は何でも N 倍高速化ができる… とそう都合よくはいきません。遅延を考えたのが下の図です。
- C0,C1,C2… と N 段の遷移関数 T 部分の遅延時間(tCT)が累積(tCT × N)
- D-FF ループの遅延が増えクロック周波数を下げないと正しく動かなくなる
- ループ遅延が十分小さくないと、最大動作周波数が下がる・周波数的に3倍遅い
(極論/理想論と現実的な価値)
- 遅延時間がゼロまたは無視できるほど小さい場合は動く
- その場合は元の1段の回路も周波数を上げられるはず → Super Sample Rate 構造は不要
なので、この発想は机上の空論で利用価値がないだろう、という見方もあるかもしれません。確かに全てのディジタル回路への適用は大風呂敷です。
今回の記事は、Super Sampe Rate 対応の回路をわかりやすく、スケーラブルに表現するのに、この構造の表現は使えるのでは、という発想とモデルベース設計で作ってみた例の紹介です。
回路の性能は、index 計算を頑張って作った場合と同等かもしれませんが、構造をわかりやすくしてミスの可能性を減らし、検証・デバッグしやすいという利点があると考えています。
(FIR フィルタの多段化表現)
FIR フィルタのデザイン表現の為、下記の様にとらえ方を変更しています。

遷移関数 T ⇒ シフト接続、出力関数 G ⇒ 積和演算という変更になります。
- 積和演算(Vector 内積、”・“)が組み合わせ回路で遅延ゼロと見なすと変更ではなく同じ
- シフト回路は何段接続しても遅延ゼロ(ただし、配線遅延は無視)
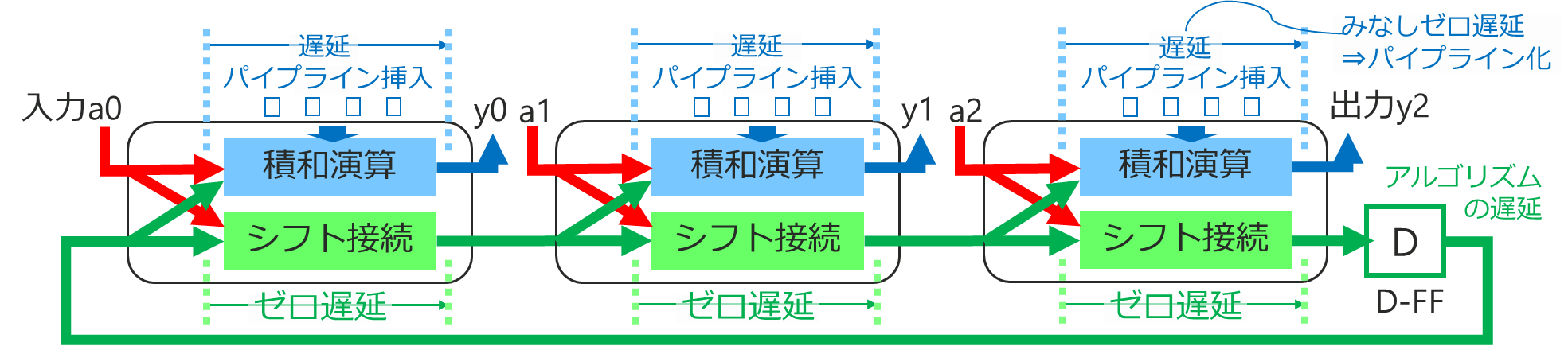
実装では、下の図の様に、積和演算はパイプライン化されます。
- 出力 y や入力 a も通常 D-FF を経由して接続
- 入力から出力へクロック単位のレイテンシがある
- 規則的に作る限り、並列出力はそろって遅れて要素間でずれが生じることはない
DSP Builder (Advanced) のパイプライン化される部分について、下記の様な考え方と Handbook のどこかに書かれていたと思います。そちらにも合っています。
- SampleDelay はアルゴリズムのための遅延(1クロック前のデータ) を表現
- ロジックや演算はゼロ遅延とみなして表現し、パイプラインは後で tool が自動挿入
下記の DSP Buider のデモの 1/3 位の所でも同じ様な事を言っています。
DSP Builder でのデザイン例は後で述べます。
(HDL 記述検討)
DSP Builder ではなく RTL 記述での設計も検討しつくりかけてみたのですが未完成です。
今回発想した構造の部分は generate 文でスッキリと書けるかな、とは思っています。
genvar i;
generate
for(i = 0; i < super_ratio; i = i + 1) begin: GLOOP
FIRCOMB STAGE #(9) (
.clk(clock),
.rst(reset),
.din(drin[ 32*i+31 : 32*i ]),
.pst(stin[ i ]),
.nst(stin[ i+1 ]),
.dout(dout[ 32*i+31 : 32*i ])
);
end
endgenerate
動作確認はできていないのでなにか間違っているかもしれませんが、ループの D-FF を除いた多段化される部分はこんな感じです。
super_ratio が段数 N のパラメータ、din, dout が入出力信号、stin が各ステージ間で状態を表す信号を接続するための 2 次元配列の wire 変数です。
(問題点予想、ただし配線については未評価)
積和演算部分は段数が増えると下記の現実的な問題が出てくると考えられます。
- 段数に比例してハードウェア量が必要
- 配線のファンアウトや引き回し距離が伸びて、配線量・配線遅延も増大
(ディジタル回路の考察方法など、今後の可能性)
なお、Mealy Machine 表現と実際の回路の構成についてより考察すると下記の様な点で面白いことが分かりそうな気がしています。(分析・分類の手法として)
- シフトレジスタのフィードバックは実際にはループにはなっていない
- パイプライン回路(挿入後)を Mealy Machine として捉えなおす
学術・研究レベルですでに行われている内容かもしれませんが、現場のハードウェア設計エンジニア向けにかみ砕いたノウハウが得られるかもと思います。
また、行列演算とか AI 分野の Convolution とか同じ積和演算関係なのでそちら向けの設計にも思考法として使えないか、とも考えています。
また何かいい発想・知見が得られればいずれ紹介しようとは思います。
(CPU/ソフトウェア についての考察)
今回の発想を CPU(Processor)設計やソフトウェアの記述に当てはめてみるとどうか? 力不足ですがちょっとだけ考えてみましたのでそのあたりお詳しい方になにかヒントになればと思い書いておきます。
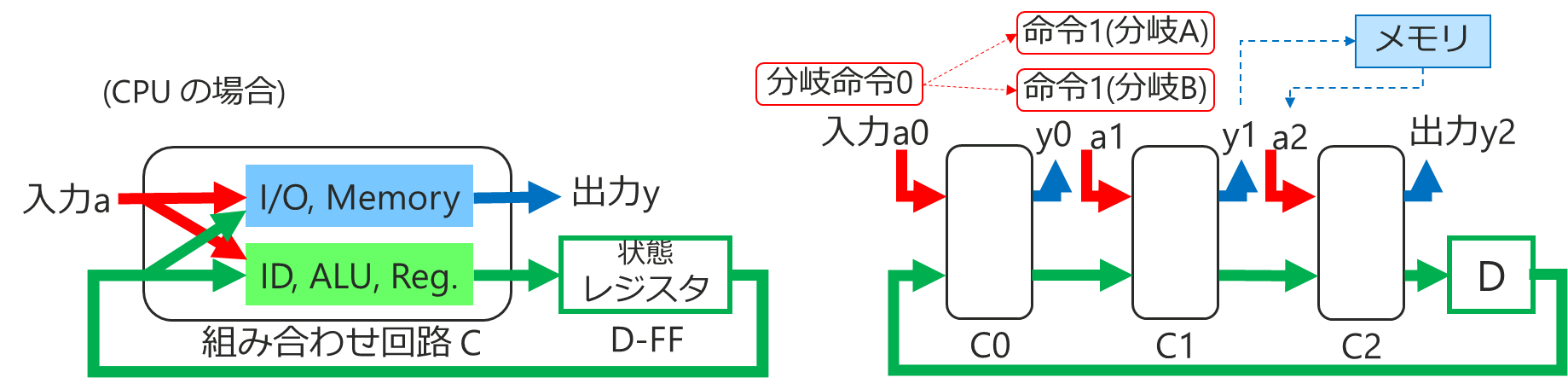
(CPU の場合)
1マシンサイクルでの計算はそれなりのロジックになりますので累積遅延で限界がありますが、N=4 でも 8 でもこの構造で作れるとメリットがあるとして考えてみますと...
- (入)出力は I/O やメモリアクセス(これが問題になる)
- 遷移関数は命令デコード(ID)、ALU やアドレス計算、内部レジスタアクセス
- 分岐命令があると、その後の Stage で入力の命令(候補)をメモリから複数読み出す必要
- 分岐処理のためウェイトを入れるとせっかく増やしたハードが無駄になる
- 同じメモリへの読み書きが近接していた場合、ある Stage の出力をすぐ後の入力にする場合もある
- メモリアクセスの交通整理や分岐命令の処理を考慮しないといけない
- ソフトのコンパイラも含めてもっと広い範囲で検討しないといけない
(ソフトウェア表現の場合)
この構造でソフトコードを書いてみるとどうなるか? 考察してみました。
当方、ソフトウェアのスキルは高くないので大したことが無い点はご容赦ください。
同じ様な図で見飽きた、コードでの例でないところもすみません。。。
C 言語だと HLS (高位合成)でハードウェア化もできるので、それを意識してこの様な構造で書いたソフトウェアを、ハード化せずに CPU 等で処理した場合を考えてみます。
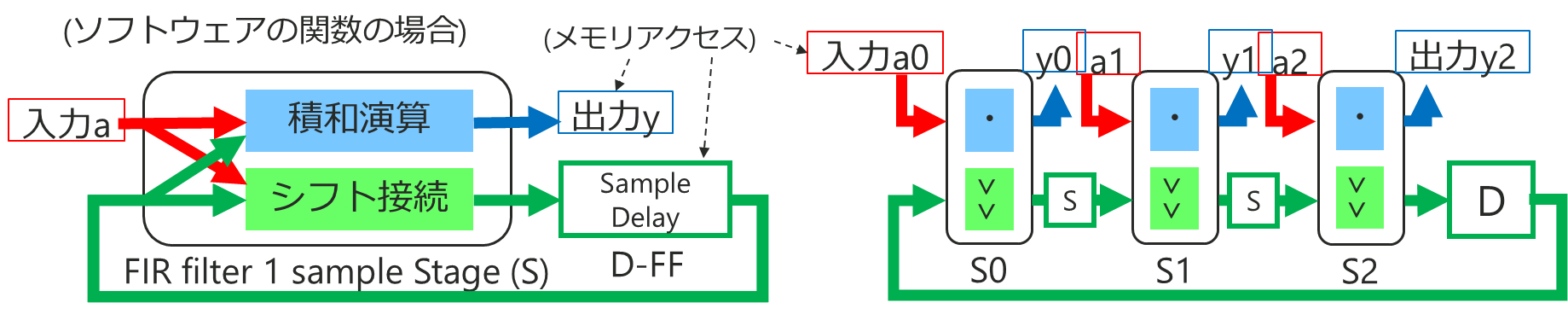
- 状態変数を含む入力、出力のデータはメモリ上で受け渡し
- ステージ間の信号はソフトウェアとして処理する場合はメモリ上で受け渡し [S]
- ハードの場合信号線の接続関係でコンパイル時に最適化されたところが、メモリアクセスが必要
- ソフトウェアのコンパイラが冗長なメモリアクセスを最適化すれば問題なし
- 上記最適化が効かない場合、段数に比例して冗長なメモリ領域とアクセスが増える可能性
ソフトウェア側は詳しくないので最適化はされるのかどうかはわかりません...(ここまで)
(ここで、元のハードウェア実装の話に戻ります。)
DSP Builder / Simulink での設計
DSP Builder (Advanced)、Simulink モデルで N=4、tap 数は 9 の単精度浮動小数点数 FIR フィルタモデルを作成してみました。
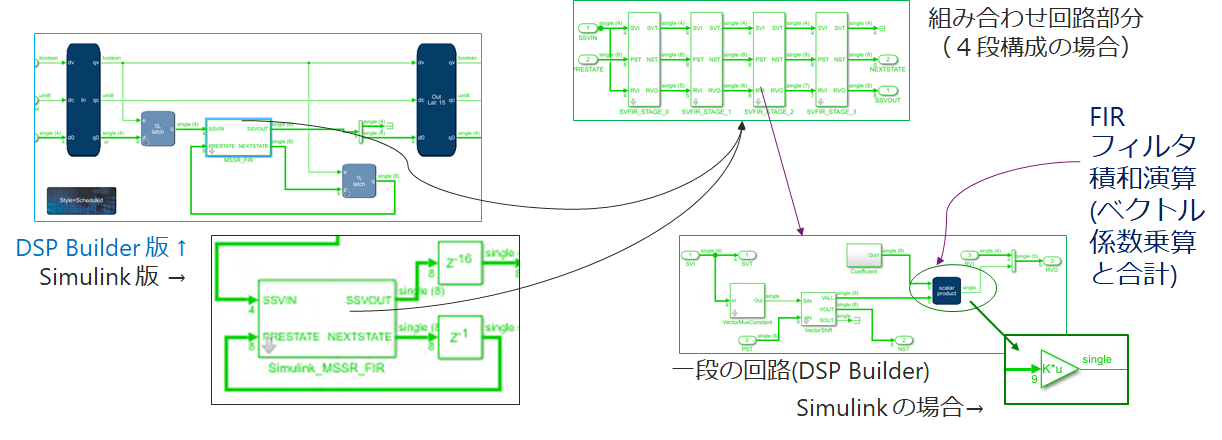
こんな感じの仕上がりになっています。
- DSP Builer 部分も Simulink オリジナルブロック(Gain) でもほぼ同じ構造で作成
- 組み合わせ回路部分の Subsystem は、マスクを設定してパラメータにより段数を変更可能
- 段数可変の仕組みはカスケードするブロックと接続を更新するスクリプト記述をマスクの初期化部分に記述する必要あり
生成された VHDL を Quartus Prime (Standard) でコンパイルし、結果のレポートを見ますと、予想通り、ハードウエアの DSP ブロックは 1 段の分量 4 倍、Fmax はほとんど同じで得られました。
- Arria 10 10AX066K2F35I1LG ターゲット(適当に選択)、Fmax = 430MHz くらい
- リソース: Logic: 351 ALMs, DSP: 36 blocks (全て Floating Point mode), memory 0
- DSP Builder 部分のレイテンシは 15
Simulink シミュレーション結果は下記の様になっています。
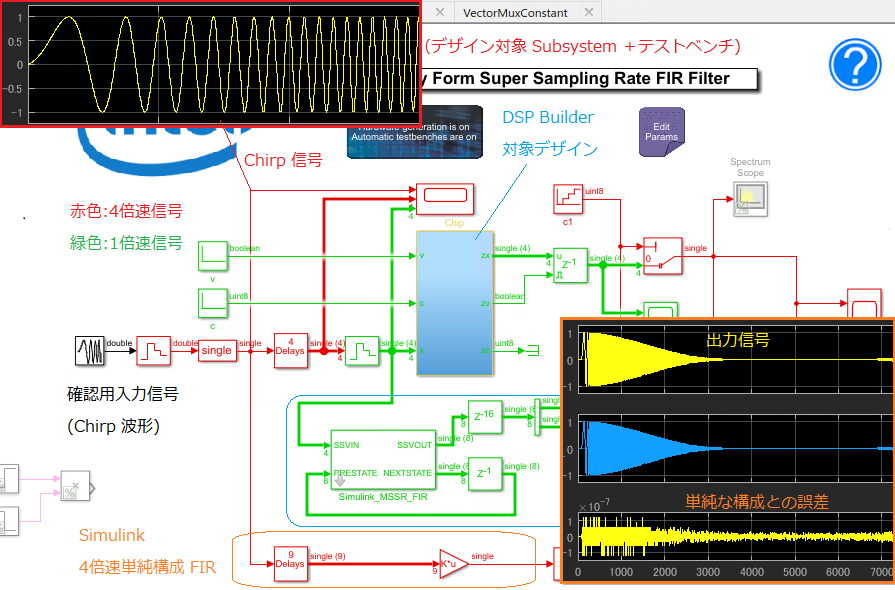
- モデルファイルの top でテストベンチ回路を表現
- 4倍速のデータ列から並列に変換した1倍速のデータを作成(Super Sample Rate 表現)
- Chirp(sweep) 波形を入力して周波数により通過/抑制となることを確認(FIR フィルタ)
- リファレンスとして、4倍速いレートの Gain ブロック1個で表現した FIR を表現(最下段)
- Super Sample Rate 表現 FIR の計算は、Simulink 版は誤差なし
- DSP Builder モデルの方は浮動小数点数の LSB レベルの誤差あり
積和の順番や丸めの問題か、振幅 1 の入力に対し 10^-7 程度の誤差が生じています。単精度浮動小数点数の仮数部ビット幅は 24 なので、2^-24 ≒ 0.6 x 10^-7 で LSB 程度の誤差と考えてよいですが、実用上、多くの場合許容できるような程度と思います。
(実機確認:MAX10 10M08 評価キット)
実機確認は、手持ちボードが乏しいため、上記 Arria 10 向けデザインでは行っていません。

スペックを下記の様に下げて、写真の MAX10 10M08 評価キットで動かしてみました。
DSP Builder の良さとしてはターゲットデバイスを変更しての設計が楽にできる事です。
(全体のレイテンシが変わるので、見直さなければならない箇所が皆無ではありませんが)
- 動作クロック 50MHz、Super Sample Rate 比率(段数)N=2、tap 数は 9
- DSP Builder 部分は入出力 16bit 固定小数点、計算は半精度浮動小数点数(float16_m10)
- DSP Builder 部分のレイテンシは 31
精度を下げたので、Simulink シミュレーションで誤差は 10^-3 と出ました。(妥当)
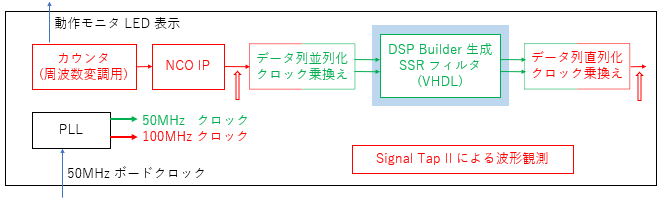
テスト回路は下図の様な構成で作っています。
カウンタ、PLL、NCO IP は IP カタログから生成、並べ替え・クロック乗せ換えと組み立ては Verilog HDL で記述し DSP Builder 生成の VHDL をはめ込んでいます。
2 倍速の 100MHz で作った Sweep 波形に 50MHz の2段構成で FIR フィルタ処理を行います。
さすがに Low Cost Device で容量小さめなのでこれでリソースは目一杯近く使っています。

Signal Tap II での波形観測結果は想定通り、Sweep 波形の周波数変化で出力振幅が変化しました。
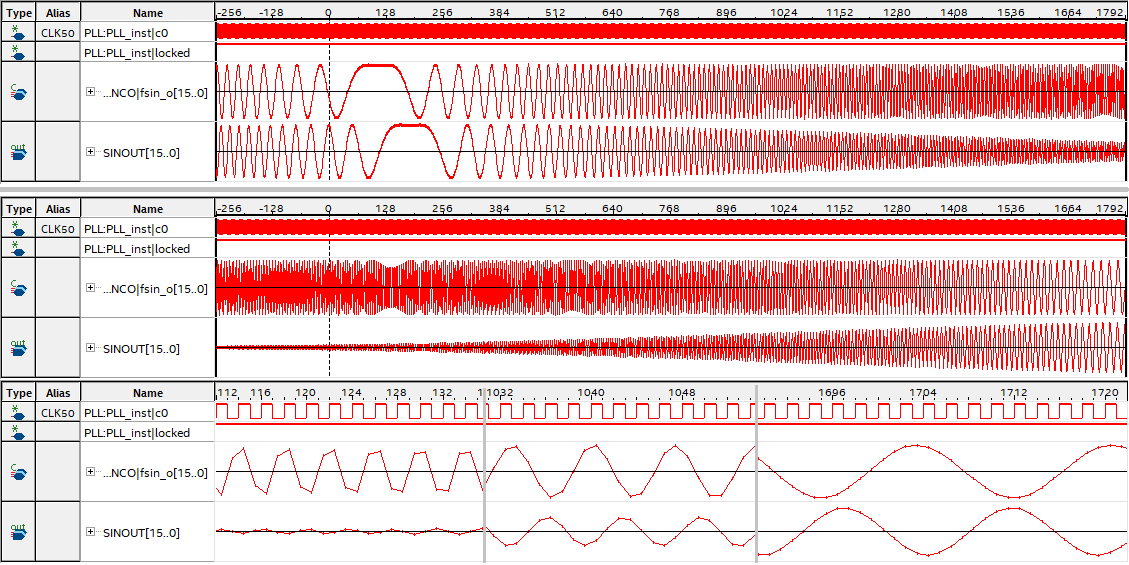
上段が周波数が下がるタイミング、中段が上がるタイミングで下段は後者の部分拡大です。
この様に、今回発想の方法で問題なく Super Sample Rate 構造の FIR フィルタが作成できることが確認できました。
(まとめ)
Mealy Machine を変形、組み合わせ回路部分を多段化する形で Super Sample Rate データ系列の FIR フィルタをスケーラブルに表現することができました。
検討で得られた知見や今後の方向は下記になります
- 実際には限界がある(多段部分の累積遅延、ハード量や配線での限界)
- ディジタル回路のとらえ方(分析や分類)としての考察
- 行列演算とか AI 分野の Convolution とかに使えないか
- HW や SW の表現方法の比較論、SW 処理の高速化(最適化)についての疑問
また、HDL での設計例や、DSP Builder /Simulink モデルの詳細についても機会(元気)があればまた投稿させていただきます。ご閲覧ありがとうございました。
(文中に記載されている会社名、商品名は各社の商標または、登録商標です。)
(追記)
本記事の DSP Builder / Simulink のモデルで使用している組み合わせ回路部分(N段カスケード)を構成するための記述方法について、Simulink カテゴリのほうで記事を投稿しましたのでご興味があればご覧ください。
モデルの内容の解説を下記に投稿しました。