はじめに
最近『ゼロから作るDeep Learning 2』で自然言語処理の勉強をしていて、備忘を兼ねてword2vecについてまとめてみました!
この記事では、word2vecの仕組みを「本当にゼロから」実装しながら学んだことを、できるだけ丁寧に・分かりやすく紹介するので良かったら見てみてください!!
word2vecの発展として、RNNの解説もしているのでもしよかったら見てみてください!!
word2vecとは?
そもそも単語のベクトル表現って?
自然言語の単語を機械が理解するためには、数値に変換する必要があります。よくあるのが one-hotベクトル ですが、これは単語同士の意味的な距離を表現できません。
# ↓ こんな感じ
[0, 1, 0, 0, 0] # you
[1, 0, 0, 0, 0] # shark
[0, 0, 1, 0, 0] # love
# → you・sharkは(代)名詞という意味で近いが、ベクトル空間だけでは表現できない!
そこで登場したのが 分散表現(Distributed Representation) です。
意味的に近い単語はベクトル空間でも近くなるように学習する仕組みで、その代表格が word2vec になります。
分散表現
以下のように、one-hotでは you も shark も love もベクトル上は全く等距離なのに対し、分散表現では「意味的に近い」単語が近い位置にマッピングされます。
# One-hotベクトルの例(次元: 5)
you → [0, 0, 1, 0, 0]
shark → [0, 1, 0, 0, 0]
love → [1, 0, 0, 0, 0]
# 分散表現(学習済みベクトル)
you → [0.21, -0.45, 0.87]
shark → [0.19, -0.44, 0.90] # youとは似た者同士
love → [0.80, 0.10, -0.60]
このように、分散表現では、you と shark のような比較的意味が近い(文脈が似る)ことが空間上で表現できるのです。
word2vecの2つのモデル
word2vecは主に2つのモデルがあります。
- CBOW(Continuous Bag of Words):文脈から単語を予測
- Skip-gram:単語から文脈を予測
どちらも入力層・中間層・出力層の3層構造で、重み行列がそのまま単語のベクトル表現(分散表現)になるのがポイントです。
ちなみに、単純なCBOW, Skip-gramでは計算コストが高すぎるという弱点があるため、以下のような処理を間に挟んで実行するのがスタンダードらしいです。
- Embedding(ベクトル空間の圧縮)
- Negative Sampling(負例をサンプリングして学習に使用)
CBOWモデルの実装
CBOW(Continuous Bag of Words)モデルは、「前後の文脈」から「中央の単語」を予測するアーキテクチャです。
例:I like sharks. You ? sharks. He like sharks. She like sharks. Right?
(※小さなコーパスでの説明になるため、文法等は無視してください。。)
→「You」「sharks」から「?」を求めるイメージ
ここでは、レイヤー構造をクラス化した SimpleCBOW の実装を紹介しつつ、コードの意味を詳しく解説します。
では、実際のコードを見ていきましょう。
以下コードがSimpleCBOWの全体像になります。
※なお、MatMulレイヤやSoftmaxWithLossレイヤはすでに用意済みとします。
※以下コードはこちらを引用させていただきました。
import sys
sys.path.append('..')
import numpy as np
from common.layers import MatMul, SoftmaxWithLoss
class SimpleCBOW:
def __init__(self, vocab_size, hidden_size):
V, H = vocab_size, hidden_size
# 重みの初期化
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(H, V).astype('f')
# レイヤの生成
self.in_layer0 = MatMul(W_in)
self.in_layer1 = MatMul(W_in)
self.out_layer = MatMul(W_out)
self.loss_layer = SoftmaxWithLoss()
# すべての重みと勾配をリストにまとめる
layers = [self.in_layer0, self.in_layer1, self.out_layer]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
# メンバ変数に単語の分散表現を設定
self.word_vecs = W_in
def forward(self, contexts, target):
h0 = self.in_layer0.forward(contexts[:, 0])
h1 = self.in_layer1.forward(contexts[:, 1])
h_avg = (h0 + h1) * 0.5
score = self.out_layer.forward(h_avg)
loss = self.loss_layer.forward(score, target)
return loss
def backward(self, dout=1):
ds = self.loss_layer.backward(dout)
da = self.out_layer.backward(ds)
da *= 0.5
self.in_layer1.backward(da)
self.in_layer0.backward(da)
return None
このモデルでは次のような処理を行います:
-
__init__
- 語彙数(V)と中間層の次元数(H)を受け取り、重みや勾配の容器を作成
-
forward
- 各単語を単語ベクトル(W_in)に変換し、Vで平均を取る
- 出力側の重み(W_out)を使ってスコアを算出
- Softmaxで確率化してターゲットの単語と比較し、損失を計算
-
backward
- 逆伝播で勾配を計算
各構成要素の解説
1. __init__ メソッド
ここでは、語彙数(V)と中間層の次元数(H)を受け取り、各レイヤの初期化と重み・勾配の初期値がまとめられた容器を作成します。
①語彙数と中間層の次元数を受け取る
V, H = vocab_size, hidden_size
V:語彙数
H:中間層の次元数
なお、Hが大きいほど単語の意味をより豊かに表現できるのですが、その分計算コストが大きくなってしまうため、その塩梅が大切です。
②入出力の重み行列(語彙ID → ベクトル変換用)を初期化
# 重みの初期化
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(H, V).astype('f')
ここでは、 入出力の重み行列(語彙ID → ベクトル変換用) を初期化しています。
W_inは[V, H]型の行列に、W_outは[H, V]型の行列の各データにランダムな数値を挿入しています。
なお、0.01はランダム値のスケールを小さくして初期学習を安定させる目的で行なっています。
加えて、.astype('f')は32ビットのフロート型(float32)に変換することでメモリを節約しています。
③レイヤを生成
# レイヤの生成
self.in_layer0 = MatMul(W_in)
self.in_layer1 = MatMul(W_in)
self.out_layer = MatMul(W_out)
self.loss_layer = SoftmaxWithLoss()
ここでは、word2vecの使われる各レイヤを初期化しています。
MatMulレイヤでは、入力値に対して重みとの内積を出力します。
④すべての重みと勾配をリストにまとめる
# すべての重みと勾配をリストにまとめる
layers = [self.in_layer0, self.in_layer1, self.out_layer]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
②〜③で生成した重みやレイヤをリストでまとめています。
⑤単語の分散表現を初期化
# メンバ変数に単語の分散表現を設定
self.word_vecs = W_in
メンバ変数に単語の分散表現を設定しています。
これがCBOWから求めたい分散表現(= 単語間の関係性)になります。
2. forward メソッド(順伝播)
大まかなには以下の様な処理を行なってます。
- 2つの文脈単語を
W_inでベクトル化(h0,h1) - ベクトルの平均をとって
h_avgを作成 -
W_outをかけてスコアを出す - ターゲットと比較し損失を返す
①単語の分散表現を初期化
h0 = self.in_layer0.forward(contexts[:, 0])
h1 = self.in_layer1.forward(contexts[:, 1])
in_layer0とin_layer1レイヤでは 文脈(context)の単語ベクトルを生成 しています。
なお、in_leyerが2つ定義されているのは、今回contextが2つあるためです。
イメージとしては以下になります。
「I eat bread.」 → context:[ I, bread ] target:[ eat ]
→ contextが2つあるから、in_layerが2つ定義している
②単語ベクトルからスコアを出力
h_avg = (h0 + h1) * 0.5
score = self.out_layer.forward(h_avg)
out_layerでは、 平均した単語ベクトルからスコアを出力 しています。
具体的には、in_layer0とin_layer1で求められた単語ベクトルの和から平均を取って、重みW_outとの内積(= スコア)を出力します。
③損失から勾配を取得
loss = self.loss_layer.forward(score, target)
return loss
②で求めた出力値からSoftmaxWithLossレイヤを通して、損失を求めます。
言い換えると、 モデルがどれだけ間違った推論をしたか を求めます。
3. backward メソッド(逆伝播)
大まかなには以下の様な処理を行なってます。
- 出力層から誤差を逆伝播
- context2語分の平均だったため、勾配を 0.5 倍してそれぞれに分配
①損失関数の逆伝播
ds = self.loss_layer.backward(dout)
ここでは、softmax関数及び損失関数から、 スコアに対する損失の勾配 を求めています。
②中間層の逆伝播
da = self.out_layer.backward(ds)
①で求めた勾配から以下の勾配を求めています。
- 重み
W_outの勾配 - 平均単語ベクトル
h_avgの勾配
例えば、W_outの場合、W_outをどう調整すれば損失が減るかを計算しているイメージです。(= 勾配)
③入力層の逆伝播
da *= 0.5
self.in_layer1.backward(da)
self.in_layer0.backward(da)
入力層の順伝播では各単語ベクトルの和の平均を求めました。
そのため、元に戻すために0.5をかけています。
あとは、入力層の勾配を求めて終わりです。
Skip-gramモデル
こちらはCBOWの逆で、1つの単語からその周囲の文脈を予測する形式です。
例:I like sharks. ?0 like ?1. He like sharks. She like sharks. Right?
(※小さなコーパスでの説明になるため、文法等は無視してください。。)
→「like」から「?0」「?1」を求めるイメージ
- CBOWの出力層が1つであったのに対して、ターゲットが複数存在する分、出力層も複数になる
- 単語の分散表現の精度や低頻度の単語では、CBOWより優れている
- 学習速度ではCBOWの方が優れている
分散表現の正体は重み行列だった!?
ここまで実装してきて気づくのは、実は 分散表現(単語ベクトル)の正体は、モデルが学習した重み行列W_in(あるいはW_out)そのもの だということです!
特にCBOWモデルでは、入力層にある W_in が「各単語に対応する単語ベクトル」を保持していて、これこそがまさに単語の意味をベクトルで表した 分散表現 の本体なのです。
学習が進むにつれて、意味的に似た単語(IとYouなど)は似たベクトルになっていき、この W_in を使えば「単語間の距離=意味的な近さ」を評価できるようになります。
実験してみた:単語の意味は本当にベクトルに宿るのか?
i [-0.32524088 -0.18620428 2.0526676 0.3084023 -1.9294733 ]
like [ 1.4720454 -1.3610317 -2.4738932 -1.3957747 1.3359051]
sharks [-2.00644 1.4744333 1.6221061 2.2876415 -0.26866663]
. [ 0.63513064 -1.5589677 -0.13443974 -0.09589648 2.234503 ]
you [-1.2287176 1.314618 0.59635144 1.1488862 -1.315046 ]
too [-0.4152239 1.1136645 -1.7693648 0.1781921 0.8826593]
he [-1.589313 1.5803062 1.4276375 1.5701383 -2.035321 ]
she [-1.2137684 1.2662815 0.6632496 1.1201724 -1.3627746]
right [-1.5883118 1.8926656 -1.109615 1.4353355 -0.14227109]
? [ 1.8778818 -1.7863336 2.1310813 -1.9476782 1.1779776]
実際に求めた分散表現になります。
似たような単語(i, you, he, she)で見比べてみると・・・
i [-0.32524088 -0.18620428 2.0526676 0.3084023 -1.9294733 ]
you [-1.2287176 1.314618 0.59635144 1.1488862 -1.315046 ]
he [-1.589313 1.5803062 1.4276375 1.5701383 -2.035321 ]
she [-1.2137684 1.2662815 0.6632496 1.1201724 -1.3627746]
ある程度似通った値になっているかと思います。
ですが、意味合い的に全く似ていない単語(i, like, too)で見比べてみると・・・
i [-0.32524088 -0.18620428 2.0526676 0.3084023 -1.9294733 ]
like [ 1.4720454 -1.3610317 -2.4738932 -1.3957747 1.3359051]
too [-0.4152239 1.1136645 -1.7693648 0.1781921 0.8826593]
先ほどよりはまとまりが無いように思います。
今回はコーパスが非常に小さい(単語数:20個程度)ため推論結果が少しバラバラになってしまいましたが、何万何十万のコーパスの場合はもう少し精度が上がると思います。
求めた分散表現から次元圧縮などを経て、プロットしたグラフが以下になります。
↓
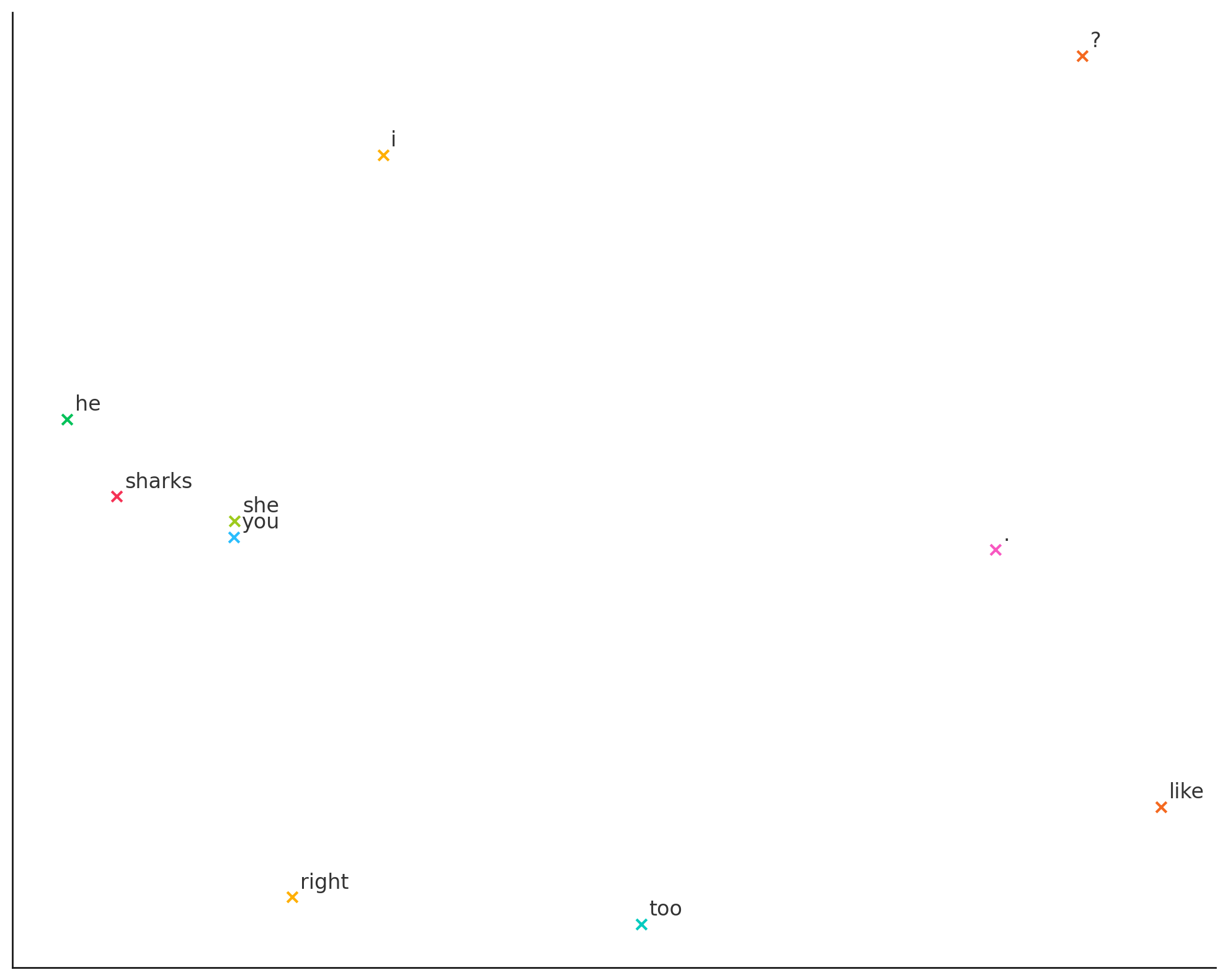
右側がごちゃってますが、やはり似た単語は同じところでプロットされているかと思います。
なお、学習が終わったあとは、各単語のベクトル表現(分散表現)からコサイン類似度を計算することで、意味的に近い単語ほど高い類似度を示すことが分かります。
`you` に近い単語TOP5
she 0.9992
he 0.9825
sharks 0.8619
right 0.7098
i 0.5796
`he` に近い単語TOP5
she 0.9885
you 0.9825
sharks 0.8613
i 0.7157
right 0.5707
つまり、コサイン類似度で評価すると、 高いスコアが出る=意味的に関係のある単語ほどベクトル空間内で近い位置にプロットされる = 似た者同士! と判断できます。
以上のことから、単語の意味が各分散表現に宿っているといえるのではないでしょうか。
有名な king - man + woman ≒ queen みたいなベクトル演算も、上記理由から行えるのです!
おわりに
今回は、CBOWを中心としたWord2Vecの仕組みについて解説しました。
Negative Sampling や Embedding などの改良手法もありますが、今回はひとまずここまでとしたいと思います。
普段使っているLLMが、入力された文章をどのように解析しているのか、少しブラックボックスのように感じていましたが、Word2Vecを学ぶことでその裏側の仕組みが少し見えてきた気がします。
また、Word2Vecが「単語間の関係性」を学習するのに対し、Doc2Vecのように「文節間の関係性」を対象に学習する手法もあることを知ることができました。
今後は、RNN や Attention機構 など、より発展的なトピックについても学びながら、記事としてまとめていきたいと思います。
RNN の解説記事はこちらになります!
↓
最後まで読んでくださり、ありがとうございました!
もし記事が参考になったら、「いいね」してもらえるとすごく励みになります!
また、内容に誤りや気になる点があれば、遠慮なくご指摘していただけると嬉しいです!
他にもいろいろな記事を投稿しているので、もしよかったら見てみてください!
参考
Word2Vecを理解するにあたって、以下の資料を参考にさせていただきました。
先人たちの知見に感謝です!