More than 3 years have passed since last update.

71日目 SIRモデルでこの自粛がいつまで続くか予測してみました

Python

Last updated at 2020-04-13Posted at 2020-04-12

#SIRモデルを計算してみました。

新型コロナの流行はいつまで続くんだろう。
昨日のNHKスペシャル「新型コロナウイルス瀬戸際の攻防〜感染拡大阻止最前線からの報告〜」を参考に計算してみました。

##SIRモデルとは
感染症の流行〜収束を計算するのに使われる方程式です。

##PythonでSIRモデルを実装する
Pythonで実装したコードがscipython.comにありましたので、使わせていただきました。

The SIR epidemic model

SIR.py

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# Total population, N.
N = 1000
# Initial number of infected and recovered individuals, I0 and R0.
I0, R0 = 1, 0
# Everyone else, S0, is susceptible to infection initially.
S0 = N - I0 - R0
# Contact rate, beta, and mean recovery rate, gamma, (in 1/days).
beta, gamma = 0.2, 1./10 
# A grid of time points (in days)
t = np.linspace(0, 160, 160)

# The SIR model differential equations.
def deriv(y, t, N, beta, gamma):
    S, I, R = y
    dSdt = -beta * S * I / N
    dIdt = beta * S * I / N - gamma * I
    dRdt = gamma * I
    return dSdt, dIdt, dRdt

# Initial conditions vector
y0 = S0, I0, R0
# Integrate the SIR equations over the time grid, t.
ret = odeint(deriv, y0, t, args=(N, beta, gamma))
S, I, R = ret.T

# Plot the data on three separate curves for S(t), I(t) and R(t)
fig = plt.figure(facecolor='w')
ax = fig.add_subplot(111, axis_bgcolor='#dddddd', axisbelow=True)
ax.plot(t, S/1000, 'b', alpha=0.5, lw=2, label='Susceptible')
ax.plot(t, I/1000, 'r', alpha=0.5, lw=2, label='Infected')
ax.plot(t, R/1000, 'g', alpha=0.5, lw=2, label='Recovered with immunity')
ax.set_xlabel('Time /days')
ax.set_ylabel('Number (1000s)')
ax.set_ylim(0,1.2)
ax.yaxis.set_tick_params(length=0)
ax.xaxis.set_tick_params(length=0)
ax.grid(b=True, which='major', c='w', lw=2, ls='-')
legend = ax.legend()
legend.get_frame().set_alpha(0.5)
for spine in ('top', 'right', 'bottom', 'left'):
    ax.spines[spine].set_visible(False)
plt.show()

#インフルエンザの場合
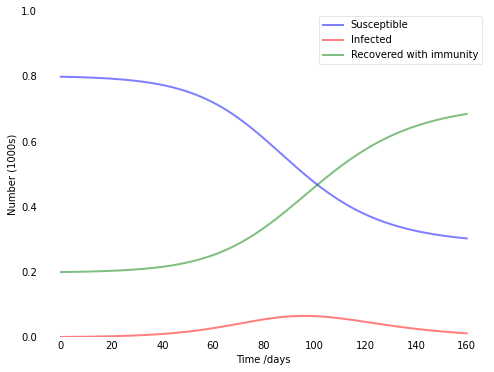
まず、例として設定されていたインフルエンザをみてみます。

##インフルエンザ(免疫なし）

N  =1000 #人口、1000人というと学校や会社、町内会あたり？
I0 =1    #感染者。最初は１人。
R0 =0    #回復して免疫を獲得した人。最初は0人
S0 =N - I0 - R0 #免疫をもたず感染しやすい人。最初はN-I0-R0人
beta =0.2       #1日に感染させる人数
gamma =1./10    #回復率
t =160          #期間(日数)

ひとりの感染者が1日0.2人に感染させます。
感染期間は10日間。
回復して免疫を獲得すると、この後は接触しても感染しません。
免疫ありが半分以上になると収束に向かいます。

ひとりのキャリアからピークまで67日、15.3%、153名が感染し収束となりました。
インフルエンザで学級閉鎖するとき、こんな感じですよね。

##インフルエンザ(免疫20%)
インフルエンザのシーズン前にワクチンを打って免疫を獲得したケースを考えてみます。
まず、２割の人が免疫を獲得したところにインフルエンザが流行した場合です。

# Initial number of infected and recovered individuals, I0 and R0.
#I0, R0 = 1, 0
I0, R0 = 1, (N*0.2)

２割の人が免疫を持つだけで、流行がずいぶん抑えられました。ワクチンすごい。

##インフルエンザ(免疫50%)

2019年度のインフルエンザワクチンの定期接種率は50%でした。

# Initial number of infected and recovered individuals, I0 and R0.
#I0, R0 = 1, 0
I0, R0 = 1, (N*0.5)

完全に抑えられています。
こうなれば安心ですね。

#COVID-19の場合

新型コロナの場合を考えてみます。
東京都、武漢市など1000万人の都市を想定、感染期間は３週間(21日)としました。
その他の性質はインフルエンザと同じとしました。

##COVID-19(免疫なし）

N  =10000000 #人口1000万人(東京、武漢を想定)|
I0 =1        #感染者。最初は１人。
R0 =0        #回復して免疫を獲得した人。最初は0人
S0 =N - I0 - R0 #免疫をもたず感染しやすい人。最初はN-I0-R0人
beta =0.2       #1日に感染させる人数 
gamma =1./21    #回復に要する日数の逆数 
t =160          #期間(日数)

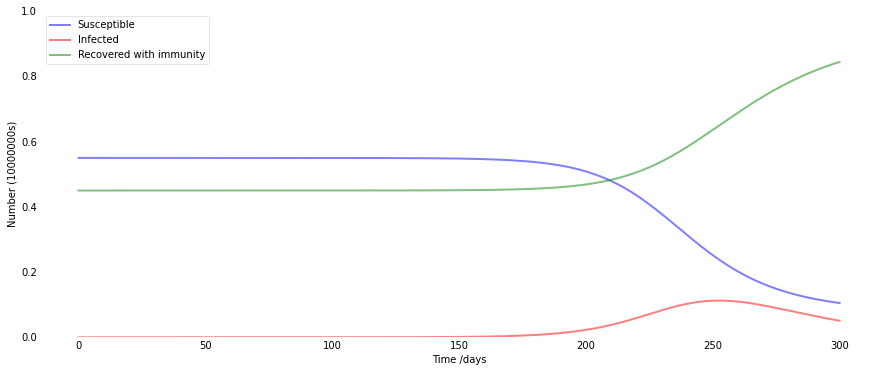
感染期間が21日になるだけで、ピーク時の感染者数が42%、420万人と凶悪なウイルスに進化しました。
このうち2割が発症し、1%が死亡となると・・・
84万人が発症、4万2千人が死亡、228日で収束します。

地獄です。

このグラフを見た後、数日ほど滅入ってしまいました。

しかしこのツイートを見かけて、ひょっとしたら希望はあるかもと思いました。

衝撃の調査結果‥
ドイツで最初に新型コロナの集団感染が起こったハインスベルク郡で、免疫調査をまず約500人に行ったところ、何と約15％の人が感染済みだったと‥。
ハインスベルクのPCR検査での人口10万人あたりの感染者数は604.4人、判明していた感性率はたった0.6%です‥
https://twitter.com/R3000C/status/1248594913589002240

##COVID-19(免疫15%）
今の日本も15%の人が感染済みとします。
15%の人が感染済みになるまで89日。

89日目でロックダウンして流行を止めます。

１ヶ月後に全ての人が回復し15%の人が免疫を持つとします。
ロックダウンを解除。流行が再燃するのですが、、、