ポアソン回帰モデルの予測値vs.残差プロットの解釈を教えてほしい!
解決したいこと
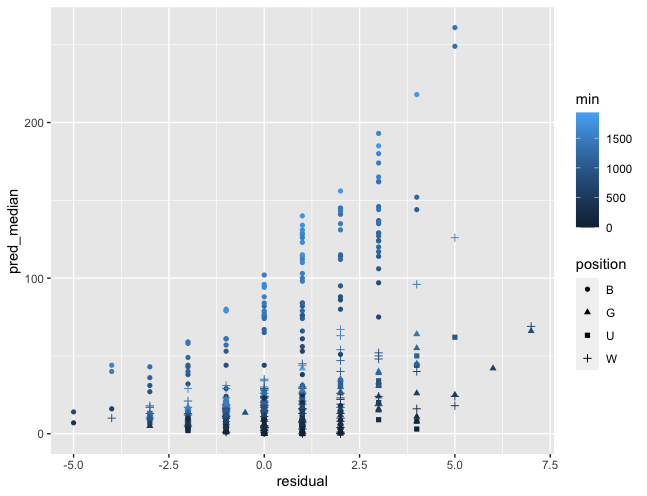
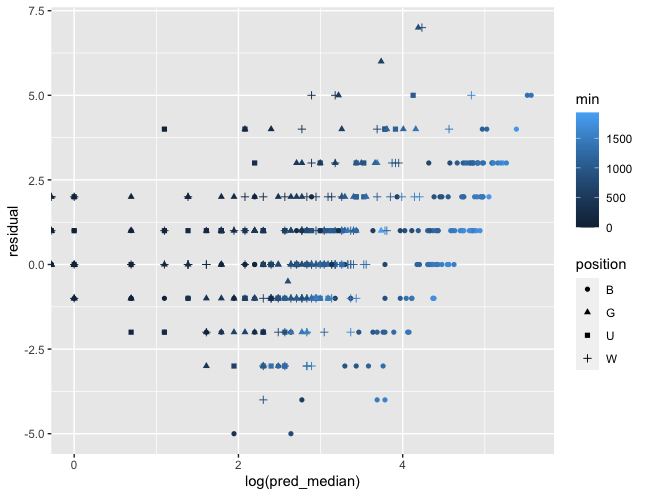
作成したポアソン回帰モデルの予測値vs.残差プロットの解釈ができない。
概要
バスケットボールのデータを題材に、ベイズ統計モデリングを練習しています。
より詳しくは、選手のポジションと単位時間あたりのオフェンスリバウンド数の関連がテーマです。
期待している結果は、ゴール近くでプレイするB(ビッグマン)はオフェンスリバウンドが多く、ゴールから離れてプレイするG(ガード)はオフェンスリバウンドが少ない、どちらの距離でもプレイするW(ウイング)はGとBの間くらいのフェンスリバウンドを記録する、つまりオフェンスリバウンド数がB>W>Gになることです(Uはポジション不明:Unknownで予想が立てられない)。
ポジションの影響を推定するためには、作成した統計モデルがデータに当てはまっていることが前提になります。そのため、統計モデルの当てはまりをチェックする一手段として予測値vs.残差プロットを調べていたのですが、解釈ができなかったので質問させていただきました。
発生している問題・エラー
統計モデルにどんな気持ちを込めたか
オフェンスリバウンドの分布と使用する確率分布の選択
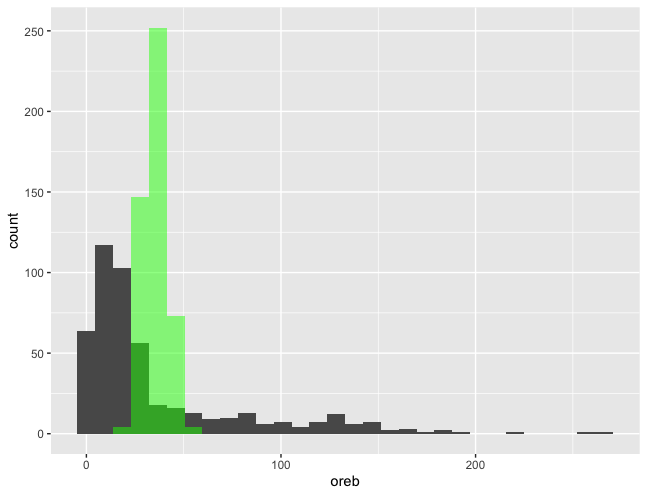
オフェンスリバウンドのヒストグラムを灰色で示します。オフェンスリバウンドは非負のカウントデータなので、ポアソン分布を確率分布として選択しました。λ=オフェンスリバウンドの平均値として、選手数と同じ数だけポアソン分布に従う乱数を発生させた結果が緑色のヒストグラムです。過分散があることが分かったので、個人差を考慮することにしました。
統計モデルの記述
ポジションは全部で4つ(G,W,B,U)なので3つのダミー変数を作成しました。X_BがBの時に1をとる変数、X_WがWの時に1をとる変数、X_UがUの時に1をとる変数です。これらの回帰係数の代表値をGと比べた時のオフェンスリバウンドへの影響と解釈することにしました。
transformed parametersのlog(MIN[n])は出場時間の対数をとったもので、オフセット項です。1分あたりのオフェンスリバウンドへの影響が推定できるように投入しています。0.01を加えているのはエラーが出ないようにするためのおまじないです。1を加えるのが一般的かもしれませんが……
個人差を考慮するためにランダム切片を投入しています。個人差は平均0・分散sigma_rに従うと仮定しました。sigma_rの超事前分布には一様分布を使っています。
最終的な統計モデルは確率分布にポアソン分布・リンク関数に対数リンク関数・線形予測子が(切片+個人差+ポジションの効果)となりました。
data{
int N;
int X_B[N];
int X_W[N];
int X_U[N];
int Y[N];
real MIN[N];
}
parameters{
real a;
real b_b;
real b_w;
real b_u;
real r[N];
real sigma_r;
}
transformed parameters{
real lambda[N];
for(n in 1:N){
lambda[n]=a+b_b*X_B[n]+b_w*X_W[n]+b_u*X_U[n]+log(MIN[n]+0.01)+r[n];
}
}
model{
r~normal(0,sigma_r);
Y~poisson_log(lambda);
}
generated quantities{
real Y_pred[N];
Y_pred=poisson_log_rng(lambda);
}
統計モデルの当てはまりを調べるために既にやったこと
いくつか試した限りでは、当てはまりは良さそうだと考えています。
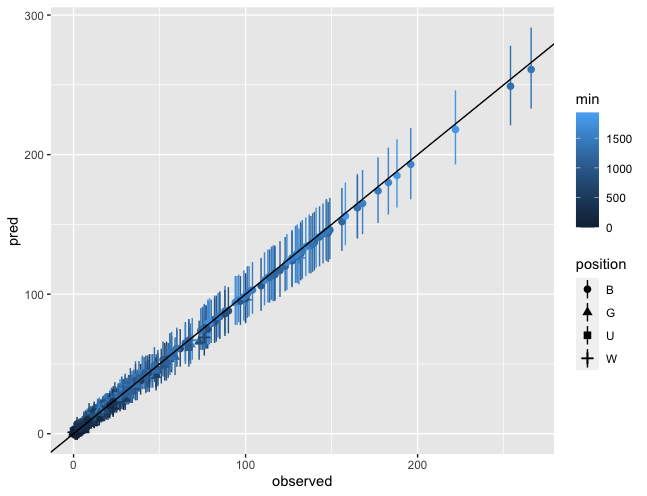
予測値と観測値のプロット
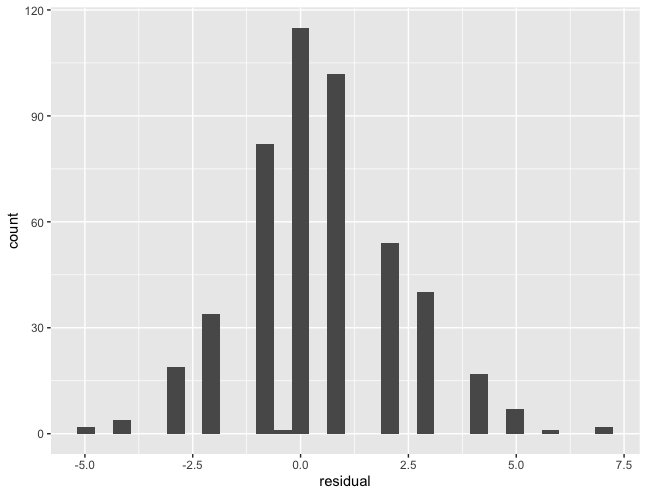
残差のヒストグラム
40分換算のポジションごとのオフェンスリバウンド数と予測値の比較
| ポジション | 観測値 | 予測値 |
|---|---|---|
| G | 0.96 | 0.78 |
| W | 1.47 | 1.15 |
| B | 2.77 | 2.61 |
有識者様、アドバイスよろしくお願いします。