自作平衡二分探索木のすゝめ 〜Splay Treeの仕組みと実装〜

1. はじめに

こんにちは、defineです。

Qiitaに記事を投稿するのは 中学校の委員分けを最小費用流で最適化してみた話 に続きこれで2回目となります。

今回は平衡二分探索木についての話をしようと思います。

2. 前提知識

前提知識として、グラフ理論の基本的な用語やC++の基本的な部分を理解できる必要があります。

3. 二分探索木とは？

要素の検索、挿入、削除を各クエリ $O(log N)$ で処理する事のできるデータ構造の事です。

ただし、要素の重複は認められません。

例えば、次のような処理ができます。

「 $2$ 入れて」「あいよ」... { $2$ }
「 $1$ 入れて」「ほい」 ... { $1,2$ }
「 $2$ ある？」「あるぞい」 ... { $1,2$ }
「 $1$ 消して」「ほい」 ... { $2$ }
「 $1$ 消して」「もうないぞい」 ... { $2$ }

二分探索木の仕組みに関してはWikipediaや蟻本が詳しいので、そちらを参照してください。

実装例を載せて、本題に移ります。

template<class T>
class BinaryTree{
    struct node{
        T val;
        node *lch,*rch;
    };
    node *root=NULL;
    node *find(node *x,T v){
        if(x==NULL||x->val==v)return x;
        if(v<x->val)return find(x->lch,v);
        return find(x->rch,v);
    }
    node *insert(node *x,T v){
        if(x==NULL){
            node *q=new node;
            q->val=v;
            q->lch=q->rch=NULL;
            return q;
        }
        if(v<x->val)x->lch=insert(x->lch,v);
        else if(x->val<v)x->rch=insert(x->rch,v);
        return x;
    }
    node *erase(node *x,T v){
        if(x==NULL)return x;
        if(v<x->val)x->lch=erase(x->lch,v);
        else if(v>x->val)x->rch=erase(x->rch,v);
        else if(x->lch==NULL){
            node *q=x->rch;
            delete x;
            return q;
        }else if(x->lch->rch==NULL){
            node *q=x->lch;
            q->rch=x->rch;
            delete x;
            return q;
        }else {
            node *q;
            for(q=x->lch;q->rch->rch!=NULL;q=q->rch);
            node *r=q->rch;
            q->rch=r->lch;
            r->lch=x->lch;
            r->rch=x->rch;
            delete x;
            return r;
        }
        return x;
    }
public:
     node *find(T v){
         return find(root,v);
     }
     void insert(T v){
         root=insert(root,v);
     }
     void erase(T v){
         root=erase(root,v);
     }
};

4. 二分探索木の問題点

$10^6$ 個の検索/挿入/削除クエリを処理する事を考えます。

ランダムケースにおいては、二分探索木はstd::setよりも高速です。

しかし、極端な例として $1,2,3,4,5...$ と挿入するとどうでしょう？

挿入時にどんどん右のノードに追加されて行き、実質Listです。

そのため、この場合 $O(N^2)$ かかってしまい非常に非効率です。

そこで、木の平衡を常に保つ「平衡二分探索木」を考えましょう！

5. 平衡二分探索木の種類

平衡二分探索木には、様々な種類があります。

代表的なものを紹介します。

5-1. AVL Tree

どのノードも左部分木の高さと右部分木の高さの差が $1$ 以下という性質があり、平衡性が高く検索が高速です。

5-2. 赤黒木

ノードに赤/黒の色をつけたデータ構造です。

任意のノードにおいて、その子孫の葉までのパスに含まれる黒ノードの数は選んだ葉によらず一定という性質があります。

std::setは通常赤黒木で実装されています。

挿入/削除が高速ですが、実装が面倒な事で知られています。絶対やりたくない

5-3. Splay Tree

木を回転させて、検索をかけたノードを根に持ってくる事で平衡を保ちます。

あるノードを根に持ってくるという操作ができるため、Link-cut Treeというデータ構造で使用されます。

今回紹介するものです。

5-4. Treap

取り敢えずランダムな場所に挿入してから、条件を満たすように上に持ってくるというヒープのような事をします。

Tree+Heapから来てるらしいです。

6. 木の「回転」

Splay Treeの紹介で「木を回転させて」という表現をしましたが、ピンと来た人は少ないのではないでしょうか。

回転と言ったら右回転と左回転があります。

平衡を保つ上で非常に重要ですので、それぞれ見ていきましょう。

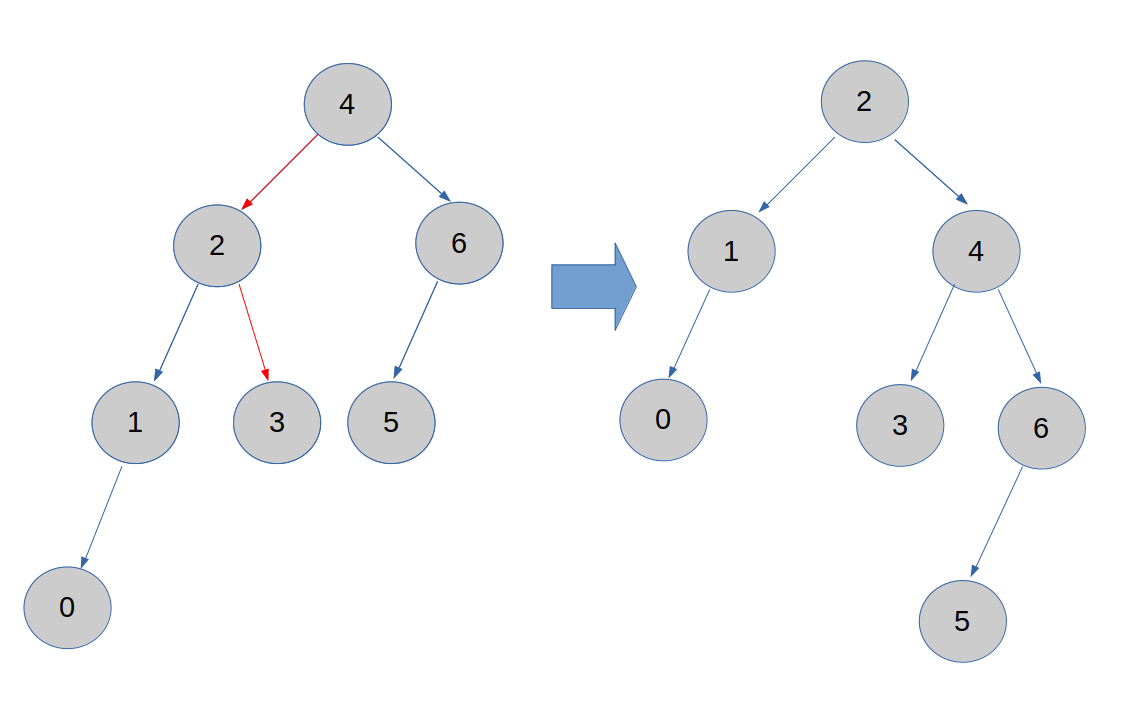
6-1. 右回転

図は、「 $4$ 」ノードで右回転をする例です。

変わるのは赤くなっているものだけです。具体的には、$4$ と $2$ が入れ替わり、$2$ -> $3$は $4$ -> $3$ になりました。

node *rightRotate(node *x){
    node *y=x->lch;
    x->lch=y->rch;
    y->rch=x;
    return y;
}

このコードで考えてみましょう。

xは 「 $4$ 」ノード、yは「 $2$ 」ノードになります。
そして、xの左の子にyの右の子を代入、つまり「 $3$ 」ノードです。
yの右の子をxにして、完成です。
戻り値は、元々xのあった場所にどのノードが代入されたかになります。

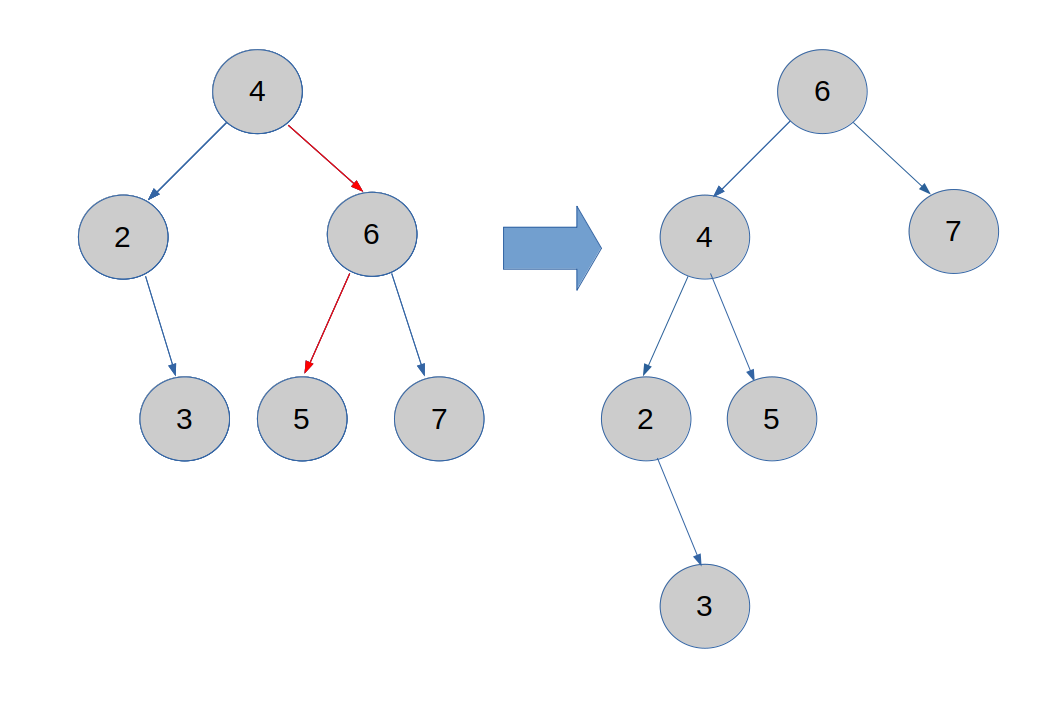
6-2. 左回転

図は、「 $4$ 」ノードで左回転する例です。

先程同様、変わるのは赤くなっているものだけです。具体的には、$4$ と $6$ が入れ替わり、$6$ -> $5$ が $4$ -> $5$ になりました。

node *leftRotate(node *x){
    node *y=x->rch;
    x->rch=y->lch;
    y->lch=x;
    return y;
}

先程同様です。
xは $4$ 、yは $6$です。
xの右の子がyの左の子、つまり $5$ になり、yの左の子をxにして完成です。
右回転を左右反転しただけですね。

7. Splay操作

Splay Treeはあるノードを根に持ってくる操作、Splay操作で平衡を保ちます。

どうやってSplay操作をするのか見ていきましょう。

実装例で上から順に解説します。

node *splay(node *x,T v){
    if(x==NULL||x->val==v)return x;
    if(v<x->val){
        if(x->lch==NULL)return x;
        if(v<x->lch->val){
            x->lch->lch=splay(x->lch->lch,v);
            x=rightRotate(x);
        }else if(x->lch->val<v){
            x->lch->rch=splay(x->lch->rch,v);
            if(x->lch->rch!=NULL)
                x->lch=leftRotate(x->lch);
        }
        return (x->lch==NULL)?x:rightRotate(x);
    }else {
        if(x->rch==NULL)return x;
        if(v<x->rch->val){
            x->rch->lch=splay(x->rch->lch,v);
            if(x->rch->lch!=NULL)
                x->rch=rightRotate(x->rch);
        }else {
            x->rch->rch=splay(x->rch->rch,v);
            x=leftRotate(x);
        }
        return (x->rch==NULL)?x:leftRotate(x);
    }
}

この関数は、現在ノードがxで、vの入ったノードをxに持ってくるという操作をする関数です。

返り値はxです。xは変化し得る事に気をつけましょう。

if(x==NULL||x->val==v)return x;

これは大丈夫でしょう。xがNULLか目的の値だったらそれを返します。

xがNULLという事は、目的の値が木の中に無かったという事を示します。

if(v<x->val){
    if(x->lch==NULL)return x;
    if(v<x->lch->val){
        x->lch->lch=splay(x->lch->lch,v);
        x=rightRotate(x);
    }else if(x->lch->val<v){
        x->lch->rch=splay(x->lch->rch,v);
        if(x->lch->rch!=NULL)
            x->lch=leftRotate(x->lch);
    }
    return (x->lch==NULL)?x:rightRotate(x);
}

これは、目的の値が現在の値より小さく、左部分木にあると考えられる場合です。
もしも左部分木がなかったら、目的の値は木の中にないのでそのままxを返します。

左の子より目的の値が小さい場合は、左の子の左部分木に目的の値があると考えられるので再帰的に操作し、xの左の子の左の子に目的の値を持ってきます。
そして、右回転する事でxとその左の子を交換します。これで、xの左の子が目的の値になりました。

左の子より目的の値が大きい場合は、左の子の右部分木に目的の値があると考えられるので再帰的に操作し、左の子の右の子に目的の値を持ってきます。
左の子で左回転する事でxの左の子と、その右の子を交換します。この時、xの左の子の右の子がなければ回転できない事に注意しましょう。これで、xの左の子が目的の値になりました。

明示はされていませんが、左の子と目的の値が同じ場合は何もしません。

この時点で、目的の値がxの左の子に格納されています。
最後に右回転する事で、目的の値の入ったノードとxを交換し、無事にxに目的のノードが格納されました（目的の値が入ったノードがある場合は）。

左の子と右の子でゲシュタルト崩壊してきた

目的の値が現在の値より大きい場合も同じなので省略します。

8. 各種クエリ

8-1. 検索クエリ

検索クエリをかける時は、Splay操作をする事で目的の値を根に持ってきます。

つまり、Splay操作をした後で根の値が目的の値と同じかどうかで、木の中に目的の値があるかどうかが分かるという仕組みです。

node *find(T x){
    root=splay(root,x);
    if(root==NULL||root->val!=x)return NULL;
    return root;
}

rootを更新するのを忘れないようにしましょう。

8-2. 挿入クエリ

挿入する時は、まず検索をかけます。つまりSplayします。

node *insert(node *x,T v){
    if(x==NULL){
        node *q=new node;
        q->val=v;
        q->lch=q->rch=NULL;
        return q;
    }
    if(v<x->val)x->lch=insert(x->lch,v);
    else x->rch=insert(x->rch,v);
    return x;
}
void insert(T x){
    if(!find(x)){
        root=insert(root,x);sz++;
    }
}

8-3. 削除クエリ

削除する時も、まず検索をかけます。つまりSplayします。

node *erase(node *x,T v){
    if(x==NULL)return NULL;
    if(v<x->val)x->lch=erase(x->lch,v);
    else if(x->val<v)x->rch=erase(x->rch,v);
    else if(x->lch==NULL){
        node *q=x->rch;
        delete x;
        return q;
    }else if(x->lch->rch==NULL){
        node *q=x->lch;
        q->rch=x->rch;
        delete x;
        return q;
    }else {
        node *q;
        for(q=x->lch;q->rch->rch!=NULL;q=q->rch);
        node *r=q->rch;
        q->rch=r->lch;
        r->lch=x->lch;
        r->rch=x->rch;
        delete x;
        return r;
    }
    return x;
}
void erase(T x){
    if(find(x)){
        root=erase(root,x);
        sz--;
    }
}

8-4. lower_boundクエリ

せっかくなので、こちらもやっておきましょう。

Splay操作の時は目的の値を根に持ってくると書きましたが、目的の値がない場合はどうなるでしょう？
答えは、目的の値より小さい最大値/目的の値より大きい最小値です。
二分探索してるのでまぁそれはそうですよね。

これを利用します。

• 根の値が目的の値以上の場合、明らかにそれが最小値なのでそれを返す。
• それ以外の場合、右部分木は全て目的の値以上なので、右部分木の中で最も小さい値を返す。

node* lower_bound(T x){
    root=splay(root,x);
    if(root==NULL||root->val>=x)return root;
    if(root->rch==NULL)return NULL;
    node *q;
    for(q=root->rch;q->lch!=NULL;q=q->lch);
    return q;
}

8-5. upper_boundクエリ

lower_boundと大して変わりません。

node *upper_bound(T x){
    root=splay(root,x);
    if(root==NULL||root->val>x)return root;
    if(root->rch==NULL)return NULL;
    node *q;
    for(q=root->rch;q->lch!=NULL;q=q->lch);
    return q;
}

9. 実装まとめ

以上のコードをまとめると、以下のようになります。

template<class T>
class SplayTree{
    struct node{
        T val;
        node *lch,*rch;
    };
    node *root=NULL;
    int sz=0;
    node *rightRotate(node *x){
        node *y=x->lch;
        x->lch=y->rch;
        y->rch=x;
        return y;
    }
    node *leftRotate(node *x){
        node *y=x->rch;
        x->rch=y->lch;
        y->lch=x;
        return y;
    }
    node *splay(node *x,T v){
        if(x==NULL||x->val==v)return x;
        if(v<x->val){
            if(x->lch==NULL)return x;
            if(v<x->lch->val){
                x->lch->lch=splay(x->lch->lch,v);
                x=rightRotate(x);
            }else if(x->lch->val<v){
                x->lch->rch=splay(x->lch->rch,v);
                if(x->lch->rch!=NULL)
                    x->lch=leftRotate(x->lch);
            }
            return (x->lch==NULL)?x:rightRotate(x);
        }else {
            if(x->rch==NULL)return x;
            if(v<x->rch->val){
                x->rch->lch=splay(x->rch->lch,v);
                if(x->rch->lch!=NULL)
                    x->rch=rightRotate(x->rch);
            }else if(x->rch->val<v){
                x->rch->rch=splay(x->rch->rch,v);
                x=leftRotate(x);
            }
            return (x->rch==NULL)?x:leftRotate(x);
        }
    }
    node *insert(node *x,T v){
        if(x==NULL){
            node *q=new node;
            q->val=v;
            q->lch=q->rch=NULL;
            return q;
        }
        if(v<x->val)x->lch=insert(x->lch,v);
        else x->rch=insert(x->rch,v);
        return x;
    }
    node *erase(node *x,T v){
        if(x==NULL)return NULL;
        if(v<x->val)x->lch=erase(x->lch,v);
        else if(x->val<v)x->rch=erase(x->rch,v);
        else if(x->lch==NULL){
            node *q=x->rch;
            delete x;
            return q;
        }else if(x->lch->rch==NULL){
            node *q=x->lch;
            q->rch=x->rch;
            delete x;
            return q;
        }else {
            node *q;
            for(q=x->lch;q->rch->rch!=NULL;q=q->rch);
            node *r=q->rch;
            q->rch=r->lch;
            r->lch=x->lch;
            r->rch=x->rch;
            delete x;
            return r;
        }
        return x;
    }
public:
    int size(){
        return sz;
    }
    node *find(T x){
        root=splay(root,x);
        if(root==NULL||root->val!=x)return NULL;
        return root;
    }
    void insert(T x){
        if(!find(x)){
            root=insert(root,x);sz++;
        }
    }
    void erase(T x){
        if(find(x)){
            root=erase(root,x);
            sz--;
        }
    }
    node* lower_bound(T x){
        root=splay(root,x);
        if(root==NULL||root->val>=x)return root;
        if(root->rch==NULL)return NULL;
        node *q;
        for(q=root->rch;q->lch!=NULL;q=q->lch);
        return q;
    }
    node *upper_bound(T x){
        root=splay(root,x);
        if(root==NULL||root->val>x)return root;
        if(root->rch==NULL)return NULL;
        node *q;
        for(q=root->rch;q->lch!=NULL;q=q->lch);
        return q;
    }
};

10. 性能評価

AtCoderのコードテスト上で、$10^6$ 個の $0$ 以上 $10000$ 未満の乱数を検索/挿入/削除する時間の平均を測りました。

これ乱数生成する方が時間かかってるんじゃ

クエリ	std::set	Splay Tree
find	131ms	173ms
lower_bound	133ms	175ms
upper_bound	131ms	179ms

続いて、$1$ 〜 $10^6$ までの数を順に挿入する時間を測りました。

std::set : 240ms
Splay Tree : 48ms

得意不得意があるようですね。速度的には問題ないようです。

まだインクリメント、デクリメントとかは実装してないけど...

11. おわりに

長い記事でしたが、最後まで読んで頂きありがとうございました。

参考文献 :
スプレー木 -Wikipedia
Splay Tree| Set 1(Search) - Geeksfor Geeks
プログラミングコンテストチャレンジブック