こんにちは、defineです。実はこの記事が初投稿です!
4/24現在、私の通う東京にある中学校も新型コロナの影響で休校措置が続いています。
新学期にある事と言えば入学式やクラス分けなど色々ありますが、この記事では私のクラスであった委員分けの話をしようと思います。
普段の委員分け
一般的に委員分けと言えばこうでしょう。
- 黒板に委員会の一覧が書かれる。
- 各委員で希望者が挙手をし、定員以内なら確定。
- 定員溢れした委員についてはじゃんけんや話し合いで決める。
しかし、今は全員が集まって話し合いをできるような環境にはありません。
では、どうすれば円満に解決することができるでしょうか?
提案した方法
私の通う中学校ではGSuiteが導入されているため、Google Classroomを用いた連絡が行われています。
私はHRのClassroomに入るのが遅れてしまったため、既に第一〜第三希望までをGoogle Formで聞く所まで決定していました。
しかし、聞いた後どうするかはまだ決められていなかったのです。
そこで、私は
第一希望に割り当てられたら10点
第二希望に割り当てられたら30点
...
のようにコストを設定し、全体のコストを最小化する方法を提案しました。
この提案は受け入れられ、実行に移される事になりました!
一般化
以下のように一般化した問題を考えます。
$N$ 人のクラスで委員分けをします。
委員会は合計 $M$ つあり、$1$ から $M$ の番号がついています。
$i$ 番目の委員会には $A_i$ 人が割り当てられます。
そこで、$N$ 人に上位 $K$ 位までの希望を聞きました。
出席番号 $i$ の生徒の希望順位 $j$ 位である委員会番号は $B_{i,j}$ である事が分かっています。
ただし、$K$ 位以内に含まれなかった委員会は全て希望順位 $K+1$ 位とみなします。
生徒が希望順位 $i$ 位の委員会に割り当てられた場合、その生徒の不満度は $C_i$ となります。
この値は全生徒で共通です。
割り当てを工夫して、不満度の合計を最小にしてください。
この問題を言い換えると、下のようなネットワークでSourceノードからSinkノードに流量 $N$ を流す時、コストを最小でいくらにできるかという問題になります。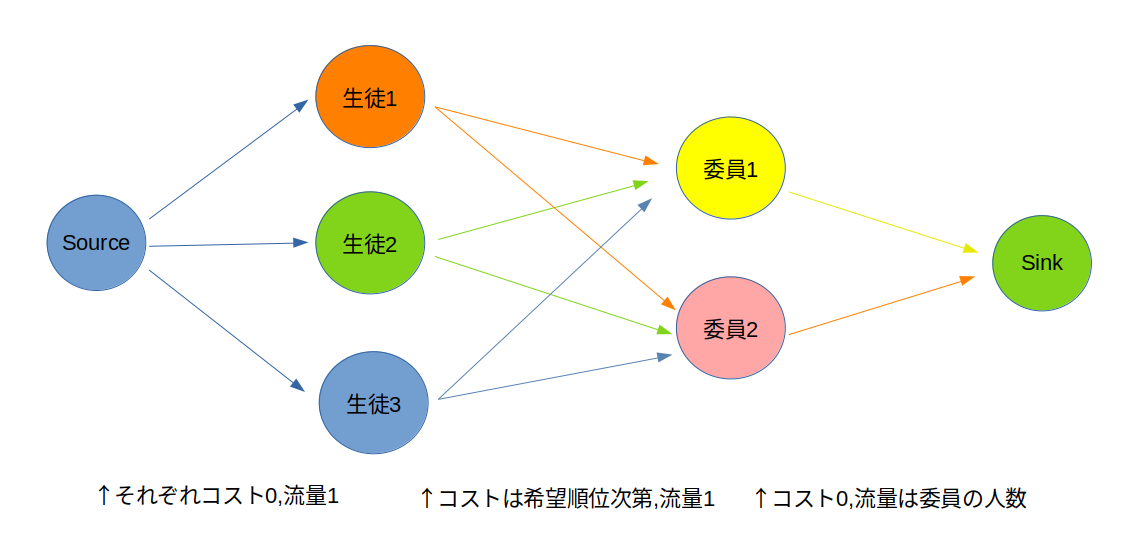
例えば、委員1の人数が2人、委員2の人数が1人と定まっている時に
生徒1 : 委員1
生徒2 : 委員2
生徒3 : 委員1
と割当てるのは、
Source -> 生徒1 -> 委員1 -> Sink に流量1
Source -> 生徒2 -> 委員2 -> Sink に流量1
Source -> 生徒3 -> 委員1 ->Sink に流量1
のように流すという意味になります。
この時かかるコストは
生徒1 -> 委員1 へのコスト
生徒2 -> 委員2 へのコスト
生徒3 -> 委員1 へのコスト
の合計となります。
それぞれの委員からSinkに流せる流量は定員と同じ数となるため、委員に定員を超える生徒を割り当てることはできません。
同様に、各生徒に流れてくる流量は $1$ なので、生徒は必ず $1$ つの委員会に所属する事になります。
これで、制約・結果ともに言い換えられている事が分かりました。
これは最小費用流問題というネットワークフローの有名問題で、Primal Dual法を用いる事で高速に解くことができます。
最小費用流問題は、ネットワークフロー入門 や蟻本に詳しいです。
入力データはGoogle Formの結果をそのまま使いたかったので、以下のようなコードを書きました。
(追記 4/26 11:10)
コードでは、全部もしくは一部を投票していない人、異なる順位に同じ選択肢を投票した人を無効として全て第一希望扱いとしています。
また、複数回投票した場合は最後に投票したものを最終結果とみなしています。
コード
# include<bits/stdc++.h>
using namespace std;
# define ll long long
# define rep(i,n) for(ll i=0;i<n;i++)
# define REP(i,n) for(ll i=1;i<n;i++)
# define inf (ll)(1e12)
# define inf2 (ll)(3e18)
# define P pair<ll,ll>
template<class T> inline void chmin(T &a, T b) {
a = min(a, b);
}
template<class T> inline void chmax(T &a, T b) {
a = max(a, b);
}
struct PrimalDual{
struct edge{
ll to,cap,cost,rev;
};
vector<vector<edge>>graph;
vector<ll>potential,min_cost,prevv,preve;
PrimalDual(ll V):graph(V){};
void add_edge(ll from,ll to,ll cap,ll cost){
graph[from].push_back({to,cap,cost,(ll)graph[to].size()});
graph[to].push_back({from,0ll,-cost,(ll)graph[from].size()-1});
}
ll min_cost_flow(ll s,ll t,ll f){
ll V=graph.size();
ll res=0;
priority_queue<P,vector<P>,greater<P>>que;
potential.assign(V,0);
prevv.assign(V,-1);
preve.assign(V,-1);
while(f>0){
min_cost.assign(V,inf2);
que.emplace(0,s);
min_cost[s]=0;
while(!que.empty()){
P p=que.top();que.pop();
if(min_cost[p.second]<p.first)continue;
rep(i,(ll)graph[p.second].size()){
edge &e=graph[p.second][i];
ll nextcost=p.first+e.cost+potential[p.second]-potential[e.to];
if(e.cap>0&&min_cost[e.to]>nextcost){
min_cost[e.to]=nextcost;
prevv[e.to]=p.second,preve[e.to]=i;
que.emplace(min_cost[e.to],e.to);
}
}
}
if(min_cost[t]==inf2)return -1;
rep(i,V)potential[i]+=min_cost[i];
ll addflow=f;
for(ll i=t;i!=s;i=prevv[i]){
chmin(addflow,graph[prevv[i]][preve[i]].cap);
}
f-=addflow;
res+=addflow*potential[t];
for(ll i=t;i!=s;i=prevv[i]){
edge &e=graph[prevv[i]][preve[i]];
e.cap-=addflow;
graph[i][e.rev].cap+=addflow;
}
}
return res;
}
};
//[0:N)->student
//[N:N+M)->Committee
//N+M->source
//N+M+1->sink
void solve(){
//input
ll N,M,K;
cin>>N>>M>>K;
vector<int>cost(K+1);
rep(i,K+1)cin>>cost[i];
vector<string>committee(M);
vector<int>capacity(M);
map<string,int>re_co,re_st;
int sum=0;
rep(i,M){
cin>>committee[i]>>capacity[i];
re_co[committee[i]]=i;
sum+=capacity[i];
}
if(sum!=N){
cout<<"Error"<<endl;
return;
}
vector<string>address(N);
vector<vector<int>>hope(N);
rep(i,N)hope[i].resize(K,-1);
rep(i,K){
int L;cin>>L;
while(L--){
string s,t;cin>>s>>s>>s>>t;
if(re_st.find(s)==re_st.end()){
re_st[s]=re_st.size();
address[re_st[s]]=s;
}
rep(j,t.size()){
if(t[j]=='('){
t=t.substr(0,j);break;
}
}
if(re_co.find(t)==re_co.end()){
cout<<"Error! "<<t<<" is undefined."<<endl;
return;
}
hope[re_st[s]][i]=re_co[t];
}
}
PrimalDual g(N+M+2);
rep(i,N)g.add_edge(N+M,i,1,0);
rep(i,M)g.add_edge(N+i,N+M+1,capacity[i],0);
int cheaters=0;
vector<bool>cheat(N);
rep(i,N){
vector<int>num(M,K);
rep(j,K){
if(hope[i][j]==-1)cheat[i]=true;
else if(num[hope[i][j]]!=K)cheat[i]=true;
else num[hope[i][j]]=j;
}
if(!cheat[i]){
rep(j,M){
g.add_edge(i,N+j,1,cost[num[j]]);
}
}else {
rep(j,M)g.add_edge(i,N+j,1,cost[0]);
cheaters++;
}
}
cout<<"コスト : "<<g.min_cost_flow(N+M,N+M+1,N)<<endl;
vector<int>stats(K);
//output
rep(i,N){
cout<<(address[i]==""?"???":address[i])<<" : ";
REP(j,M+1){
if(g.graph[i][j].cap==0){
cout<<committee[j-1];
if(!cheat[i]){
rep(k,K)if(j-1==hope[i][k]){
stats[k]++;
cout<<" ("<<k+1<<"位)";
goto ok;
}
cout<<" ("<<K+1<<"位以降)";
ok:;
}
else {
cout<<" (無効な投票です.)";
}
cout<<endl;
break;
}
}
}
cout<<endl;
int memo=0;
rep(i,K){
cout<<i+1<<"位 : "<<stats[i]<<"人"<<endl;
memo+=stats[i];
}
cout<<K+1<<"位以降 : "<<N-memo-cheaters<<"人"<<endl;
cout<<"無効 : "<<cheaters<<"人"<<endl;
}
int main() {
solve();
}
入力例
5 3 2
10 30 1000
学級代表 1
図書委員 2
風紀委員 2
6
2020/4/12 20:12:39 タプリス 風紀委員
2020/4/13 09:30:45 青葉 学級代表
2020/4/14 16:12:11 かぐや 風紀委員
2020/4/14 20:30:12 チノ 学級代表
2020/4/14 21:15:46 ミラ 図書委員
2020/4/15 22:14:30 ミラ 風紀委員
5
2020/4/12 20:13:15 タプリス 学級代表
2020/4/13 09:31:12 青葉 図書委員
2020/4/14 16:13:54 かぐや 図書委員
2020/4/14 20:32:11 チノ 風紀委員
2020/4/14 21:16:47 ミラ 学級代表
出力例
コスト : 90
タプリス : 風紀委員 (1位)
青葉 : 図書委員 (2位)
かぐや : 図書委員 (2位)
チノ : 学級代表 (1位)
ミラ : 風紀委員 (1位)
1位 : 3人
2位 : 2人
3位以降 : 0人
無効 : 0人
風紀委員なんて存在しないという事に目を瞑れば、上手く割り当てられている事が分かります。
問題点
実際のデータでの割り当てもでき、結果を発表しようとしていた時に問題が起きました。
委員分けを担当している人と発表前に相談していたのですが、
第一希望で定員超えをしていないにも関わらず、第一希望に割り当てられていない人がいる。
普段なら定員超えをしていない人は確定なのに、これでは不満が出るのではないか。
と言われたのです。
しかし、定員超えしていない委員会で第一希望を確定させてしまうのは、全体の公平性を保つ上では悪手だと考えていました。
(訂正 4/27 7:57 プログラム上の"コスト"と公平性を混同していたので直しました。)
なぜなら、定員超えしていない委員会で第一希望を確定させてしまうと、本来は第三希望でその委員会に入れた人が第四希望以降になるような事が起きてしまうからです。
実際、確定させなかった場合は出なかった第四希望以降の人が、確定させた場合は必ず出るという事が判明していました。
クラス全体でも相談をしましたが、普段との差から確定させる方が良いとの意見が多かったです。
ちなみに、第一希望が定員を超えないものを確定させるにはなるべく第一希望を増やすよう、
1位 10点
2位 10000点
3位 10030点
4位 10100点
のようにコストを変えれば良いです。
その後も議論がなされましたが、結局話し合いやじゃんけんで決めた方が一人ひとりが折り合いをつけられるので良いのではないかという結論に至りました。
(訂正 4/26 11:56 : 「プログラムを直す」ではなく、「コストを変える」でした。申し訳ありません)
分かったこと
人によって性格や思惑は異なるため、一重に最適化するというのは非常に難しいという事が分かりました。
これに似た問題としてナーススケジューリング問題がありますが、その難しさがより一層身に染みました。
最後まで読んで頂きありがとうございました。