はじめに
今回はpythonを用いた重回帰分析について取り扱います。
重回帰分析についてはこちらの記事に分かりやすくまとめられていたので、参考にしてください。
scikit-learn、tensorflow、kerasを用いて実装していきます。
使用するデータセットは有名なボストン住宅価格のデータセットです。
最初に単回帰分析についての例から解説していきたいと思います。
改良した方が良い点があれば、ご指摘いただければ幸いです。
sckit-learnで実装
最初はscikit-learnで実装していきます。
単回帰分析からやっていきましょう。
sckit-learnで単回帰分析
最初に次のモジュールをインポートします。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pandas import Series, DataFrame
import seaborn as sns
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
この中ではseabornが少しマイナーだと思う(個人の感想です)ので、こちらやこちらのサイトを参考にしてください。
簡単に書くと、seabornはmatplotlibをカッコ良く描画するためのモジュールです。
sns.set()
boston = load_boston()
boston_df = DataFrame(boston.data)
sns.set()でseabornの書式が適用されます。
boston_df = DataFrame(boston.data)の部分で、ボストンの住宅価格のデータセットをpandasのDataFrameにすることができます。
boston_dfの中身を見てみましょう。
print(boston_df.head())
print(boston_df.shape)
0 1 2 3 4 ... 8 9 10 11 12
0 0.00632 18.0 2.31 0.0 0.538 ... 1.0 296.0 15.3 396.90 4.98
1 0.02731 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 396.90 9.14
2 0.02729 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 392.83 4.03
3 0.03237 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 394.63 2.94
4 0.06905 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 396.90 5.33
[5 rows x 13 columns]
(506, 13)
以上のように、boston_dfには犯罪率や部屋の数などの13の要素のデータが506個含まれることが分かります。
head()を引数なしで指定すると最初の5つのデータを取り出すことができます。
このデータでは、DataFrameにカラム名がないので、以下のコードでカラム名を追加します。
boston_df.columns = boston.feature_names
boston.feature_namesには各々の列名が格納されています。
このコードを実行すると、以下のようにデータが変化します。ついでにboston.feature_namesの中身も確認しましょう。
print(boston.feature_names)
print(boston_df.head())
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO' 'B' 'LSTAT']
CRIM ZN INDUS CHAS NOX ... RAD TAX PTRATIO B LSTAT
0 0.00632 18.0 2.31 0.0 0.538 ... 1.0 296.0 15.3 396.90 4.98
1 0.02731 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 396.90 9.14
2 0.02729 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 392.83 4.03
3 0.03237 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 394.63 2.94
4 0.06905 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 396.90 5.33
次は、説明変数と目的変数を決定しましょう。
今回の単回帰分析では、住宅の部屋の数を用いて住宅の値段を予測します。
住宅の部屋の数はboston_dfのRMカラムに格納されています。
また、住宅価格はboston.targetに格納されています。
X = boston_df['RM']
Y = boston.target
中のデータは以下のようになっています。
print(X.shape)
print(Y.shape)
(506,)
(506,)
実は、単回帰分析を行うときにも、説明変数は2次元である必要があります。
今、説明変数であるXの次元は1次元となっているため、以下のようにして無理やり2次元に変換しましょう。
X = np.array(X)
X = X.reshape(-1, 1)
print(X.shape)
(506, 1)
reshape(-1, 1)の部分は少し分かりにくいと思うので、こちらの記事を参考にしてください。
XはもともとSeriesオブジェクトであるため、arrayオブジェクトに変換してreshapeを使いました。
それでは線形回帰モデルを作成します。
sklearn.linear_modelの中のLinearRegressionを使用しましょう。
LinearRegressionの細かい使い方はこちらの記事を参考にしてください。
model = LinearRegression()
model.fit(X, Y)
fit()の第一引数には説明変数を、第二引数には目的変数を入れましょう。
単回帰分析は以下の式で表せます。
$$y = ax + b$$
この例では、xが住宅の部屋数で、yが住宅価格です。
次のコードで係数であるaと切片であるbを出力できます。
print(model.coef_)
print(model.intercept_)
[9.10210898]
-34.67062077643857
aが正の値になっているので、部屋の数と住宅価格の間には正の相関があることが分かります。
実際にプロットをして確かめていきましょう。
predict_data = model.predict(X)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X, Y, 'o')
ax.plot(X, predict_data)
plt.show()
matplotlibの使い方や慣習についてはこちらの記事を参考にしてください。
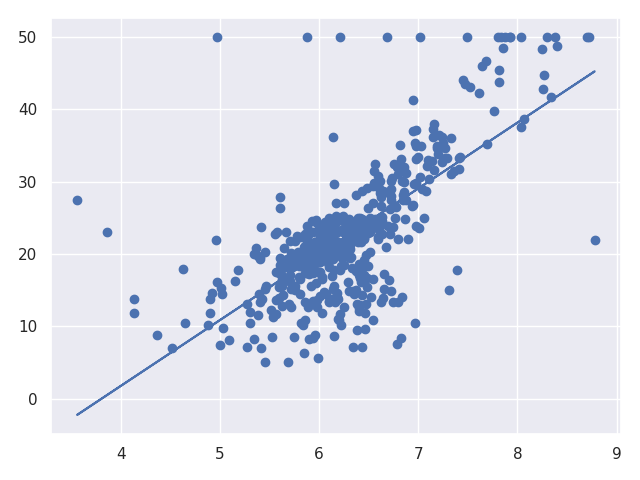
このように、線形回帰ができていることが分かります。
この線形回帰を評価していきましょう。
以下のコードで二乗和誤差と二乗和の平均を求めることができます。
print(np.sum((Y - predict_data)**2))
print(np.mean((Y - predict_data)**2))
22061.879196211798
43.60055177116956
また、次のようにすれば予想の値が真の値とどれぐらいずれているかを図示することができます。
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(X, (predict_data-Y), c='b', alpha=0.7)
ax.hlines(y=0, xmin=2.0, xmax=10)
plt.show()
y=0の線よりも上にプロットがあれば、予想の値が真の値よりも大きく、y=0の線よりも下にあれば予想の値が真の値よりも小さいことが分かります。
以上でsckit-learnでの単回帰分析は終了です。
sckit-learnで重回帰分析
次は重回帰分析を行いましょう。大体単回帰分析とコードは同じです。
import sklearn
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
sns.set()
boston = load_boston()
boston_df = DataFrame(boston.data)
boston_df.columns = boston.feature_names
X_multiple_data = boston_df.copy()
Y_target = boston.target
X_multiple_dataの中身は犯罪率や部屋の数などの13個のデータが506個格納されていて、Y_targetには住宅価格のデータが506個格納されています。
print(X_multiple_data.shape)
print(Y_target.shape)
(506, 13)
(506,)
このデータを単回帰分析と同じようにLinearRegressionクラスのfitメソッドに入れることで、重回帰分析を行うことができます。
model = LinearRegression()
model.fit(X_multiple_data, Y_target)
重回帰分析は以下の数式で表されます。
$$ y = a_1x_1 + a_2x_2 + ・・・+a_{13}x_{13} + b$$
$x_1$~ $x_{13}$はX_multiple_dataで与えているデータであるため、このモデルで与えられるのは$a_1$ ~ $a_{13}$とbになります。
係数aはmodel.coefにリストとして格納されており、切片bはmodel.intercept_に格納されています。
print(model.coef_)
print(model.intercept_)
[-1.08011358e-01 4.64204584e-02 2.05586264e-02 2.68673382e+00
-1.77666112e+01 3.80986521e+00 6.92224640e-04 -1.47556685e+00
3.06049479e-01 -1.23345939e-02 -9.52747232e-01 9.31168327e-03
-5.24758378e-01]
36.459488385089855
このままではどのデータが住宅価格に影響を及ぼしているのか分かりにくいため、以下のようにデータを整理してみましょう。
coefficint_df = DataFrame(boston_df.columns)
coefficint_df.columns = ['boston_data']
coefficint_df['Estimated Coefficient'] = pd.Series(model.coef_)
print(coefficint_df)
boston_data Estimated Coefficient
0 CRIM -0.108011
1 ZN 0.046420
2 INDUS 0.020559
3 CHAS 2.686734
4 NOX -17.766611
5 RM 3.809865
6 AGE 0.000692
7 DIS -1.475567
8 RAD 0.306049
9 TAX -0.012335
10 PTRATIO -0.952747
11 B 0.009312
12 LSTAT -0.524758
以上の結果より、住宅価格はCRIM(犯罪率)やNOX(一酸化窒素濃度)などが高いと住宅価格は低く、RM(部屋の数)などが多いと住宅価格が高くなることが分かります。
このように、重回帰分析は結果からどのデータがどのように影響しているかを簡単に分析することができます。
以上でscikit-learnによる重回帰分析は終了です。
tensorflowで実装
それではtensorflowで実装していきましょう。
tensorflowで単回帰分析
データセットを作成するまでは今までと同じですね。
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from sklearn.datasets import load_boston
import seaborn as sns
from pandas import DataFrame
sns.set()
boston = load_boston()
boston_df = DataFrame(boston.data)
boston_df.columns = boston.feature_names
X = np.array(boston_df['RM']).reshape(-1, 1)
Y = np.array(boston.target).reshape(-1, 1)
tensorflowのtensorオブジェクトは一次元配列の時に縦ベクトルなのか横ベクトルなのかを区別するため、arrayオブジェクトに変換した後にreshapeを用いて二次元配列に変換しています。
それでは次にtensorflowの計算式を定義していきましょう。
xt = tf.placeholder(tf.float32, [None, 1])
a = tf.Variable(tf.zeros([1, 1]))
b = tf.Variable(tf.zeros([1, 1]))
y = tf.matmul(xt, w) + b
yt = tf.placeholder(tf.float32, [None, 1])
xtに説明変数を与えます。
その説明変数に係数であるaをかけて、切片であるbを足し合わせたものをyとしています。以下の式ですね。
$$y=ax + b$$
このようにして計算したyと目的変数であるytとの差を小さくする方向に学習を進めていきます。次のコードを見てください。
loss = tf.reduce_sum(tf.square(y - yt))
train = tf.train.AdamOptimizer().minimize(loss)
tf.reduce_sum(tf.square(y - yt))の部分で、誤差関数を定義しています。この場合は、計算して求めたyの値と真の値ytとの二乗和誤差を誤差関数として定義して、AdamOptimizerを用いてこの誤差関数を小さくする方に変数であるaとbを更新していきます。
次のコードで学習を進めていきます。
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(100000):
if step % 10 == 0:
loss_val = sess.run(loss, feed_dict={xt: X, yt: Y})
a_val = sess.run(a)
b_val = sess.run(b)
print('Step: {}, Loss: {} a_val: {} b_val: {}'.format(step, loss_val, a_val[0][0], b_val[0][0]))
sess.run(train, feed_dict={xt: X, yt: Y})
ここの部分はtensorflowでよく用いられる部分であるため、説明は割愛します。こちらの記事などを参考にして下さい。
このようにしてtensorflowを実行することで、aとbを求めることができました。
以下のコードで、求めたaとbを使ってグラフを表示することができます。
predict_data = X * a_val[0][0] + b_val[0][0]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(X, Y)
ax.plot(X, predict_data)
plt.show()
ここまででtensorflowによる単回帰分析は終了です。
tensorflowで重回帰分析
それではtensorflowで重回帰分析を行っていきましょう。
まずはデータセットを作成していきます。
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from sklearn.datasets import load_boston
import seaborn as sns
from pandas import DataFrame
sns.set()
boston = load_boston()
boston_df = DataFrame(boston.data)
boston_df.columns = boston.feature_names
X = boston_df
Y = np.array(boston.target).reshape(-1, 1)
次はtensorflowのモデルを作成しましょう。
xt = tf.placeholder(tf.float32, [None, 13])
a = tf.Variable(tf.zeros([13, 1]))
b = tf.Variable(tf.zeros([1, 1]))
y = tf.matmul(xt, a) + b
yt = tf.placeholder(tf.float32, [None, 1])
loss = tf.reduce_sum(tf.square(y - yt))
train = tf.train.AdamOptimizer().minimize(loss)
単回帰分析と違って入力の変数は13個になっているため、xtとaを変更しています。
次のコードで学習を進めていきます。
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(100000):
if step % 10 == 0:
loss_val = sess.run(loss, feed_dict={xt: X, yt: Y})
a_val = sess.run(a)
b_val = sess.run(b)
print('Step: {}, Loss: {} a_val: {} b_val: {}'.format(step, loss_val, a_val, b_val[0][0]))
sess.run(train, feed_dict={xt: X, yt: Y})
この部分のコードはほとんど単回帰分析と変わっていません。
最後にsckit-learnの時と同じように、どのデータが住宅価格に影響を及ぼしているのかを確認してみましょう。
a_val_flatten = a_val.flatten()
print(a_val_flatten.shape)
coefficint_df = DataFrame(boston_df.columns)
coefficint_df.columns = ['boston_data']
coefficint_df['Estimated Coefficient'] = pd.Series(a_val_flatten)
print(coefficint_df)
boston_data Estimated Coefficient
0 CRIM -0.107886
1 ZN 0.046439
2 INDUS 0.020226
3 CHAS 2.687574
4 NOX -17.623962
5 RM 3.825355
6 AGE 0.000597
7 DIS -1.471468
8 RAD 0.305009
9 TAX -0.012317
10 PTRATIO -0.948393
11 B 0.009352
12 LSTAT -0.524016
以上のように、scikit-learnを用いた時とほとんど同じようなデータを求めることができました。
ここまででtensorflowによる重回帰分析は終了です。
kerasを用いて実装
最後にkerasを用いて実装していきます。kerasは重回帰分析のみ実装します。
kerasで重回帰分析
まずはデータセットを作成していきます。
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
import seaborn as sns
from pandas import DataFrame
from tensorflow.python.keras.models import Sequential
from tensorflow.python.keras.layers import Dense
sns.set()
boston = load_boston()
boston_df = DataFrame(boston.data)
boston_df.columns = boston.feature_names
X = boston_df
Y = np.array(boston.target).reshape(-1, 1)
次に、kerasのSequentialを用いてモデルを定義していきましょう。
model = Sequential()
model.add(
Dense(
units=1,
input_shape=(13,)
)
)
unitsはアウトプットの次元を表し、inputは入力データの次元を表しています。
今回はDenseを用いているため、全結合層になっています。
また、活性化関数を定義していないため、アウトプットは入力データの線形結合になっています。
次に活性化関数と誤差関数を定義していきます。
model.compile(
optimizer='adam',
loss='mean_squared_error'
)
活性化関数はAdamOptimizerを使用します。
また、誤差関数に用いるのは二乗和誤差です。
次のコードでこのモデルを実行します。
history_adam = model.fit(
X,
Y,
batch_size=50,
epochs=5000
)
バッチサイズを50に、エポック数を5000に設定しています。
次のコードで結果を評価しましょう。
coeffieit_array = model.get_weights()[0]
coeffieit_flatten = coeffieit_array.flatten()
coefficint_df = DataFrame(boston_df.columns)
coefficint_df.columns = ['boston_data']
coefficint_df['Estimated Coefficient'] = pd.Series(coeffieit_flatten)
print(coefficint_df)
model.get_weights()にはその層で用いた重みとバイアスがリストとして格納されていて、一つ目に重みに、二つ目にバイアスになっています。
後は同じように二次元配列を一次元配列に変換して、Seriesに渡しています。
結果は以下のようになります。
boston_data Estimated Coefficient
0 CRIM -0.099191
1 ZN 0.048522
2 INDUS -0.036167
3 CHAS 2.818556
4 NOX 1.265002
5 RM 5.314659
6 AGE -0.011325
7 DIS -0.996439
8 RAD 0.187641
9 TAX -0.010737
10 PTRATIO -0.432164
11 B 0.013905
12 LSTAT -0.467070
このように、kerasを用いても線形回帰を行うことができます。
終わりに
以上で今回の記事は終了です。
ここまでお付き合いいただきありがとうございました。