Atcoder ABC256A-EをPythonで解く

A - 2^N

解説にも書いてある通り。いくつか解き方があります。2^nが1<<nと同値であることは覚えておきましょう。

n = int(input())
ans1 = pow(2, n)
ans2 = 1 << n
ans3 = 2**n
if ans1==ans2==ans3: print(ans1)

B - Batters

解説通りが良いでしょう。
https://atcoder.jp/contests/abc256/editorial/4134

この問題は、マスの数が4と小さいのでシミュレーションで良いですが、ここでは、マスの数を$m$とした時に、$O(N)$で解く方法を考えます。(この問題では$m=4$固定です)
4マス以上進めたときを考えます。ここで、$i=1...N$番目に置いた駒が何マス進んだかを考えると、

• i=1: は$a_1 + a_2 + a_3 + ... + a_n$マス進む
• i=2: は$ a_2 + a_3 + ... + a_n$マス進む
• i=3: は$ a_3 + ... + a_n$マス進む

であることが分かります。このため、以下のように書けます。
最初に、1番目に置いたますが進んだマス数を求め、$a_i$を引いていくことで、その次のコマが進めたコマ数を求めていきます。

n=int(input())
a=list(map(int, input().split()))
s,ans = sum(a), 0
for i in range(n):
    if s >= 4: ans += 1
    s -= a[i]
print(ans)

C - Filling 3x3 array

公式解説の解法よりもっと少しラフに解きました。$7e7$程度の計算量で少し不安になるので、コードテストで策悪の場合を事前に試します。今回は$h1,h2,h3=30,30,30$が全列挙するのには最悪のケースです。

• 各行がh1,h2,h3になる各要素i,j,kを全列挙して求めます。最悪、$30^2$で求められますが、$30^3$で回しても良いでしょう。和が30になる候補数は406個程度です。
• h1,h2,h3になる各行の要素i,j,kを列挙したので、それらの組み合わせを全列挙します。$406^3 = 6.7e7$程度で定数倍は各列の比較3回程度です。

という考察を行ったのちにコードテストで$30,30,30$のケースで実行時間を確認して解きました。Pythonの場合、少し離れたメモリアクセスに大きな時間がかかる場合があるため少し怖かったですが、十分な実行時間だったのでそのままSubmitしました。

実装(Python)

h1, h2, h3, w1,w2,w3 = map(int, input().split())
def gen(x): # 和がxになる
    ans = []
    for i in range(1, 30):
        for j in range(1, 30):
            for h in range(1, 30):
                if i + j + h == x:
                    ans.append((i, j, h))
    return ans
can1 = gen(h1) # 和がh1になるi,h,jを列挙
can2 = gen(h2) # 和がh2になるi,h,jを列挙
can3 = gen(h3) # 和がh3になるi,h,jを列挙
ans = 0
for pat1 in can1:
    for pat2 in can2:
        for pat3 in can3:
            # これで、各横はh1,h2,h3になっている。さて、縦についてOK?
            if pat1[0]+pat2[0]+pat3[0] != w1: continue
            if pat1[1]+pat2[1]+pat3[1] != w2: continue
            if pat1[2]+pat2[2]+pat3[2] != w3: continue
            ans += 1
print(ans)

D - Union of Interval

解法1: FenwickTree O(NlogN)

この問題を以下のように言い換えます。

• 白く塗られた$N$個の壁があります
• $[L,R)$のクエリは$L$から$R-1$の壁を黒く塗る動作です。一度黒く塗ったら、複数回操作しても黒のままです。
• 最後に黒く塗られている区間を答えてください
  これは、$N$が小さいのでFenwick-Treeで解けます。区間更新を$log(N)$, 区間クエリを$log(logN)$で可能です。
• $N$個の値を0で初期化します
• $[L,R)$のクエリは$L$から$R-1$に1加算します。
• 最後に全てを見ていき(つまり、[L, L+1)の区間をクエリする)1以上の区間を答えます。これは、$N＄を全て見ていけば良いです

実装(Python)

# https://algo-logic.info/binary-indexed-tree/
class Bit:
    def __init__(self, n):
        self.size = n
        self.tree = [0] * (n + 1)
    def sum(self, i):
        s = 0
        while i > 0:
            s += self.tree[i]
            i -= i & -i
        return s
    def add(self, i, x):
        while i <= self.size:
            self.tree[i] += x
            i += i & -i
class RangeUpdate:
    def __init__(self, n):
        self.p = Bit(n + 1)
        self.q = Bit(n + 1)
    def add(self, s, t, x):
        t += 1
        self.p.add(s, -x * s)
        self.p.add(t, x * t)
        self.q.add(s, x)
        self.q.add(t, -x)
    def sum(self, s, t):
        t += 1
        return self.p.sum(t) + self.q.sum(t) * t - \
               self.p.sum(s) - self.q.sum(s) * s

n = int(input())
bit = RangeUpdate(200000 + 10)
for _ in range(n):
    l, r = map(int, input().split())
    # bit.add(a,b,x)は[a,b]にxを加算する。
    bit.add(l, r-1, 1) # [l, r)なので、[l, r-1]に1足す
ans = []
l = None # 一旦切れているものとする。
for i in range(200000 + 10): # 全ての[i,i] を見る。つながっている区間を表現。
    if bit.sum(i, i) > 0:
        # つながっている区間の時、l=None=新しいスタート？を確認
        if l == None: l = i
    else: # = 0
        # 0の区間の場合、つながっているならそこで切る
        if l is not None:
            ans.append((l, i))
            l = None
for x in ans: print(*x)

解法2: imos法

このように、加算において、区間加算をした後に１点/区間クエリをする場合はimos法が使えます。加算が行われた後に、がポイントです。加算とクエリが合わせて行われる可能性がある場合は適応できません。

実装(Python)

```Python class imos1d(): def __init__(self, n): self.n = n self.res = [0] * n def add(self, ind, val): self.res[ind] += val def solve(self): for i in range(1,self.n): self.res[i] += self.res[i-1] n = int(input()) imos = imos1d(200000 + 10) for _ in range(n): l, r = map(int, input().split()) imos.add(l, 1) imos.add(r, -1) imos.solve() ans = [] imosres = imos.res l = None # 一旦切れているものとする。 for i in range(200000 + 10): # 全ての[i,i] を見る。つながっている区間を表現。 if imosres[i] > 0: # つながっている区間の時、l=None=新しいスタート？を確認 if l == None: l = i else: # = 0 # 0の区間の場合、つながっているならそこで切る if l is not None: ans.append((l, i)) l = None for x in ans: print(*x) ```

E - Takahashi's Anguish

各人がただ一人に相手にしか不満を持たないことに注意します。不満を持っている関係を図にすると以下のように示せます。矢印は不満を持つ相手先、つまり、矢印の先が先にアメをもらっていたら不満を持つものとします。
入力全体では、このような有向グラフが最大$N$個できますが、そのうちの１つに注目します。

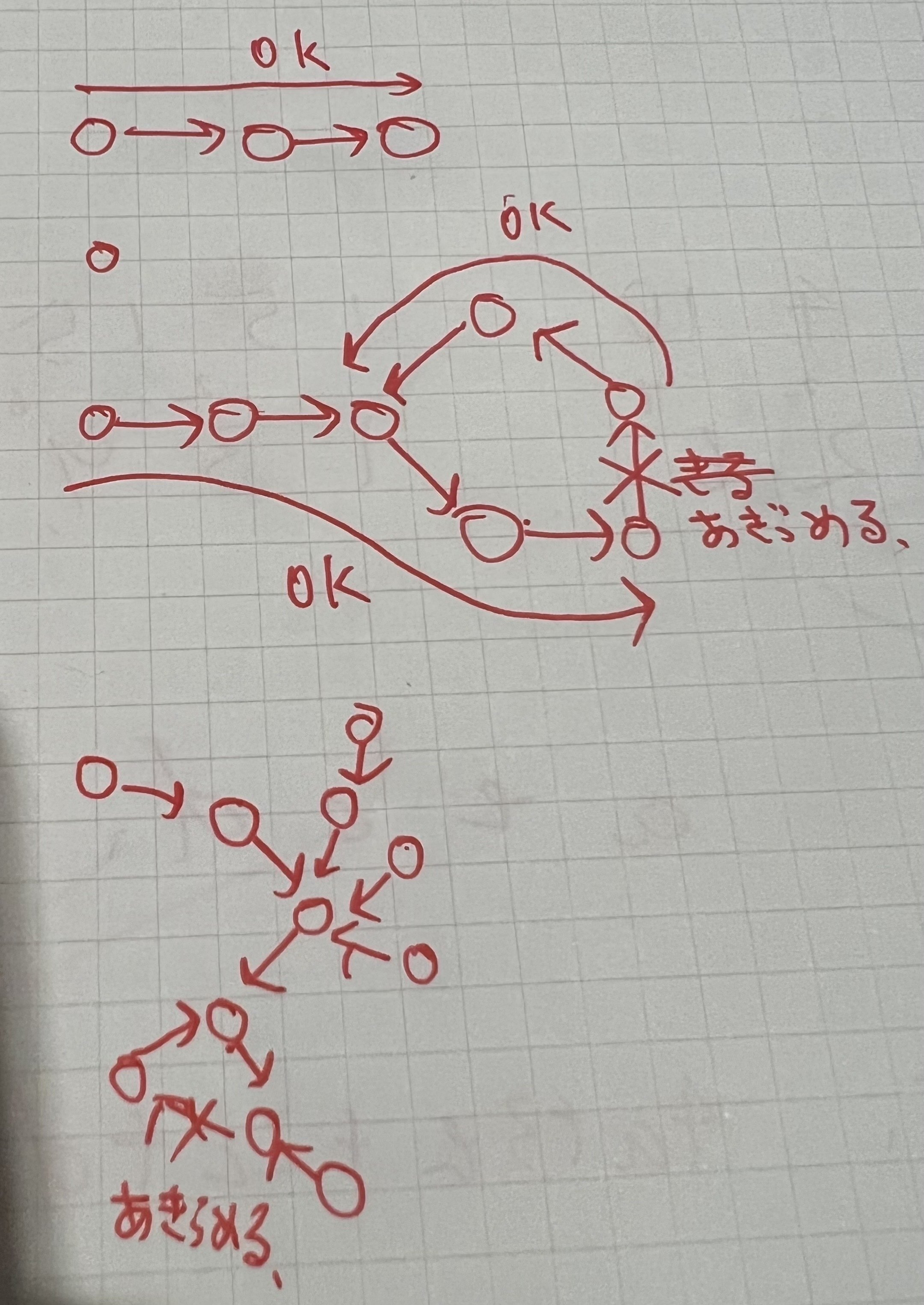
冒頭の注意を再度考えると、すべてのノードは出次が1(つまり、不満を持つ相手が1)であることに注意します。このとき、入次0 (つまり、不満を持たれない)ノードが存在すれば、そのようなノードを順番に消していくと不満は生じません。入次が1以上のノードを先に消すと必ず不満が生じます。閉路が存在しないグラフの場合、入次が0のノードから消していくことでこれは達成できます。
閉路を持つグラフはこの条件下において、その強連結成分の要素はサイクルになっており、入次が0のノードは存在しません。
この問題の条件下において、閉路がグラフに１つしか存在せず、グラフの最後にしか閉路は存在しえないことに注意します。この時、閉路となる強連結成分のただ一か所の辺が存在しなかったとすると、不満が生じないようにアメを配ることができます。
ここでの存在しなかったとするとは上記の処理をすべて行った後、その辺（の元となるノード）を選ぶことにほかなりません。

以上より、この問題は、

• グラフを連結成分に分解する
• 各連結成分について、閉路が含まれているか確認し、閉路が存在する場合はその中で最低のコストを加算する
  として解くことができます。

実装(Python)

import sys
input = sys.stdin.readline
#import pypyjit
#pypyjit.set_param('max_unroll_recursion=-1')
import sys
sys.setrecursionlimit(2000000)
def main():
    from collections import deque
    class StronglyConnectedComponent():
        def __init__(self, n):
            self.n = n
            self.g = [[] for _ in range(n)]
            self.gr = [[] for _ in range(n)]  # graph rev

        def addEdge(self, u, v):
            self.g[u].append(v)
            self.gr[v].append(u)

        def dfs(self, v):
            # 正方向のDFS
            self.visited[v] = True
            for nxt in self.g[v]:
                if self.visited[nxt]: continue
                self.dfs(nxt)
            self.vs.append(v)

        def solve(self):
            self.vs = []  # かえりがけ
            self.visited = [False] * self.n
            k = 0
            self.cmp = [None] * self.n
            # DFS1
            for i in range(self.n):
                if self.visited[i] is True: continue
                self.dfs(i)
            q = deque([])
            self.visited = [False] * self.n
            for i in self.vs[::-1]:
                if self.visited[i] is True: continue
                q.append(i)
                while len(q) > 0:
                    cur = q.popleft()
                    self.visited[cur] = True
                    self.cmp[cur] = k
                    for nxt in self.gr[cur]:
                        if self.visited[nxt]: continue
                        q.append(nxt)
                k += 1
            return k
    ans = 0
    n = int(input())
    datx = list(map(lambda x: int(x) - 1, input().split()))
    datc = list(map(int, input().split()))
    scc = StronglyConnectedComponent(n)
    edges = []
    for i in range(n):
        scc.addEdge(i, datx[i])
    scc.solve()  # 強連結成分分解する
    cmp = scc.cmp  # cmp[i] = iの所属する強連結成分の番号
    sccnodes = max(cmp) + 1  # 強連結成分の数
    cmpSize = [0] * (sccnodes)  # 各強連結成分のサイズ
    for x in cmp: cmpSize[x] += 1  # を計算
    from collections import defaultdict
    costs = defaultdict(list)
    for i in range(n):
        costs[cmp[i]].append(datc[i])
    for ke in costs.keys():
        if len(costs[ke]) == 1: continue
        ans += min(costs[ke])
    print(ans)
main()