Pythonのハッシュ衝突攻撃の考察2: 辞書のキー検索を故意に衝突させられましたの続編です。
Pythonのsetの各アクセス(追加・参照・削除)は期待時間計算量$O(1)$ですが、これを$O(N)$とするような入力を故意に生成します。
- Pythonのset実装はdictと同じオープンアドレス法が用いられているが初期値の衝突後の解決の実装はランダム探索だけを用いるdictと異なり二重ハッシュのランダム探索+線形探索(Liner Probe)でindの探索が行われる。anti-dictの入力生成を拡張することで検索の衝突を引き起こせる。
- PyPyのsetの実装はdict同じ実装のオープンアドレス法であり、dictと同一の生成コードを用いることで検索の衝突を引き起こせる。
この記事の関連としてKnuth先生のThe Art of Computer ProgrammingのVol. 3, Sec. 6.4(探索-ハッシュ法)が非常に興味深いです。
はじめに
setやdictのアクセスは、あるkeyに対してメモリ上の探索をし対応する値があるかを高速に処理できることが望ましいです。この探索にはハッシュ法(分散記憶法)が用いられています。ハッシュ法では、まず最初にハッシュ関数等で最初の格納位置候補initindを求めます。次にが衝突に発生した場合の解決を行い、最終的にその値が格納される位置indを決定します。
この衝突解決の仕方は言語のデータ型毎に異なります。C++のunordered_mapとunorded_setはinitvalの先にLinked-Listを持つLinked-List法(連鎖法)で解決します。Pythonではindに直接値を持つオープンアドレス法が用いられこれからkeyを求めるためにPythonのdictとPyPyのdictとsetは二重ハッシュが、Pythonのsetでは二重ハッシュと線形探針(Liner Probe)を組み合わせた方法が用いられています。
尚、C++のmapやsetではハッシュ法探索ではなく、二分木探索で実装されています。
体験する
MojaCoderに問題を投稿しました。無対策のset解法はTLEで落ちます。
言語毎のデータ構造と探索手法
ここまでと今回紹介するデータ構造の管理手法と期待・最悪時間計算量は以下の通りです。
| 言語 | 構造 | 探索の手法 | 期待時間計算量 | 最悪時間計算量 |
|---|---|---|---|---|
| C++ | set | 二分木 | $O(logN)$ | $O(logN)$ |
| C++ | map | 二分木 | $O(logN)$ | $O(logN)$ |
| C++ | unordered_set | ハッシュ法(Linked-List法) | O(1) | O(N) |
| C++ | unordered_map | ハッシュ法(Linked-List法) | O(1) | O(N) |
| Python | dict | ハッシュ法(二重ハッシュを用いたオープンアドレス法) | O(1) | O(N) |
| PyPy | dict | ハッシュ法(二重ハッシュを用いたオープンアドレス法) | O(1) | O(N) |
| Python | set | ハッシュ法(二重ハッシュと線形探針を用いたオープンアドレス法) | O(1) | O(N) |
| PyPy | set | ハッシュ法(二重ハッシュを用いたオープンアドレス法) | O(1) | O(N) |
振り返り1: C++のハッシュ法(Linked-List法)
C++のunordered_set/unordered_mapでは現在のデータ構造のサイズを基にしたlinked-listを指すテーブルを持ちます。まず、入力値(key)のハッシュを得て、modを取りinitindを定めます。各initineに対応するlinked-listの各要素はkeyを持つポインタindの要素で存在を管理・値を格納します。これがLinked-List法を用いて衝突を解決するハッシュ法です。
入力がランダムの場合、indexはうまくばらけて各linked-listは浅い状態になります。テーブルのサイズを動的に変化させることで、平均計算量$O(1)$でのアクセスが可能です。しかし、毎回同じinitindとなるようなkeyをN個入力すると特定のlinked-listの深さをNとすることが可能です。C++20であれば85229ul * iというkeyを$2e5$個入るようにすればanti-unordered_set/mapが実現できます。
振り返り2: Pythonのdictのハッシュ法(二重ハッシュ)
C++と同じように現在のデータ構造のサイズを基にした大きさのテーブルを持っておきます。ただし、テーブルの要素はlinked-listではなく入力値keyと値valueだけを持ちます。keyは最初のinitvalをハッシュ関数で定め、疑似乱数を用いたランダムプローブ(2つ目のハッシュ関数)で空いているテーブルの要素indが見つかるまで検索します。これはいわゆる二重ハッシュを用いたオープンアドレス法としてindの探索を行います。
pythonのソースコードより、dictの検索を行うind計算は以下のような疑似乱数を用いたランダムプローブで計算されます。
const size_t mask = DK_MASK(keys); /* 今のハッシュサイズ相当のマスク (例えばint32) */
size_t i = hash & mask; /* hashは最初オリジナルindex*/
Py_ssize_t ix = dictkeys_get_index(keys, i); /* 一発目の検索。これで空きが見つかれば以下のforは回らない*/
/* perturb = 疑似乱数 = index候補 */
for (size_t perturb = hash; ix >= 0;) { /* dictkeys_get_indexが0 = 空きがあたるまで検索 */
perturb >>= PERTURB_SHIFT; // PERTURB_SHIFT = 5 でstaticです
i = (i*5 + perturb + 1) & mask;
ix = dictkeys_get_index(keys, i);
}
この探索はkey毎に少ない回数で衝突しないindを発見できることが期待されます。ところが、Pythonのハッシュ衝突攻撃の考察2: 辞書のキー検索を故意に衝突させられましたで見たように、あるkeyを入力した際のind候補を先読みして入力し、keyのinitindと同じinitind候補を生成する$key+(mask+1)$という値を入力しておくとkeyへのアクセスを$O(N)$とすることができます。
get2ndIndex = lambda ind: (ind * 5 + 1) & mask
ind = get2ndIndex(targetnum)
for i in range(1,N):
arr += [ind]
ind = (ind * 5 + 1) & mask
を$2e5$個入るようにすればanti-dictが実現できました。
Pythonのsetの場合(二重ハッシュと線形探針)
Pythonのsetもオープンアドレス法を用いているのですがdictと同じ入力をsetに入れても高速に動作してします。これはsetは二重ハッシュに加えて線形探針を行っているためです。
import time
n = 200000
mask = (1<<17) - 1 # 0xffff
fill = 40000
arr = [mask+2]
x = 6 # magic number
for i in range(1,fill):
arr += [x]
x = (x * 5 + 1) & mask
arr += [1]*(n-len(arr))
start = time.time()
d = dict()
for x in arr: d[x]=True
print("dict elapsed_time:{0}".format(time.time() - start) + "[sec]")
start = time.time()
s = set()
for x in arr: s.add(x)
print("set elapsed_time:{0}".format(time.time() - start) + "[sec]")
"""
dict elapsed_time:15.362972259521484[sec]
set elapsed_time:0.011216878890991211[sec]
"""
Pythonのソースコードでsetobject.c -> set_lookkey()を見ます。
#define LINEAR_PROBES 9
#define PERTURB_SHIFT 5
while (1) {
entry = &so->table[i];
probes = (i + LINEAR_PROBES <= mask) ? LINEAR_PROBES: 0;
do {
if (entry->hash == 0 && entry->key == NULL)
return entry; // 空ならその要素を使う
}
entry++;
} while (probes--);
perturb >>= PERTURB_SHIFT;
i = (i * 5 + 1 + perturb) & mask;
}
i = (i * 5 + 1 + perturb) & mask;などdictと似ている部分があります。このコードは次のように動作します。
- keyからhash(SipHash)を計算しinitindとして最初のind候補とします。数値の場合は
mod (2**61-1)なので競技プログラミングでは入力そのものと考えて良いでしょう。また現在のsetのサイズに基づいたmaskが決まります。 - indが使用中(空きでない)間以下を行います
-
ind,ind+1,ind+2...ind+LINEAR_PROBESが空いていれば抜けます。(線形探針) -
ind + LINEAR_PROBESまで空きがないなら、perturb >>= PERTURB_SHIFTして、ind = (ind * 5 + 1 + perturb) & mask;とし、再びループします。(二重ハッシュ)
-
- 空きのindexが見つかったのでentryとして返して利用します
このように、ベースとなるindの計算はdictと二重ハッシュで求められ、各ind毎に先LINEAR_PROBES個が空きかを線形探針します。
例を示します。
dictの場合は[6, 31, 156, 781, 3906, 19531, 32120, 29529, 16574, 17335]というように探索されました。
setの場合は[6,7,8,...,15, 31,32,33,...,40, 156,157,158...165, ...]というように探索されます。
このため、dictのコードをベースとして線形にLINEAR_PROBES個を入力し、対象としたいkeyのinitind同じinitindを生成する$key+(mask+1)$という値を入力することで、対象としたいkeyのアクセスを$O(N)$とすることができます。
n = 200000
hashnum = 50000
LINEAR_PROBES = 9
get2ndIndex = lambda ind: (ind * 5 + 1) & mask
listCollision = []
mask = (1<<17) - 1 # 0xffff
targetnum = 1
inserted = set()
for j in range(LINEAR_PROBES+1): listCollision.append(mask + 2 + j) # ind = 1
for j in range(LINEAR_PROBES+1):
ind = get2ndIndex(targetnum) # ind = 6->31->156...
for i in range(1,hashnum//LINEAR_PROBES):
listCollision.append(ind+j)
ind = (ind * 5 + 1) & mask
for i in range(n-len(listCollision)): listCollision.append(targetnum)
print("len=", len(listCollision))
import time
start = time.time()
s = set()
for x in listCollision: s.add(x)
print("set elapsed_time:{0}".format(time.time() - start) + "[sec]")
"""
len= 200000
set elapsed_time:6.333585023880005[sec]
"""
できました!$2e5$個のデータをsetにaddするだけで6.3秒以上かかっています。
PyPyのsetの場合(二重ハッシュ)
Pythonのsetは二重ハッシュと線形探針でしたが、PyPyのsetは二重ハッシュのみです。コードで確認しましょう。
まず、コードがうまく動作しないことを見ていきます。CodeForcesのCustom Invocation(や、AtCoderのカスタムテスト)でPythonに有効なanti-setのコードをPyPyで実行します。
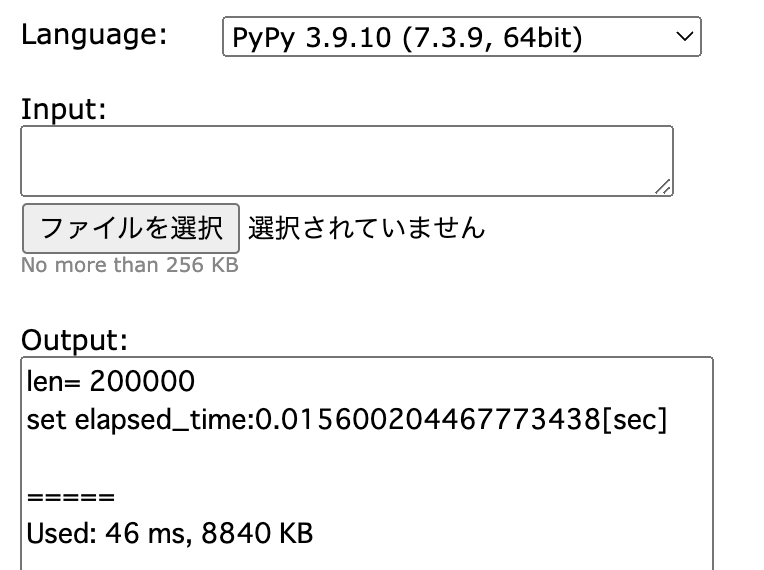
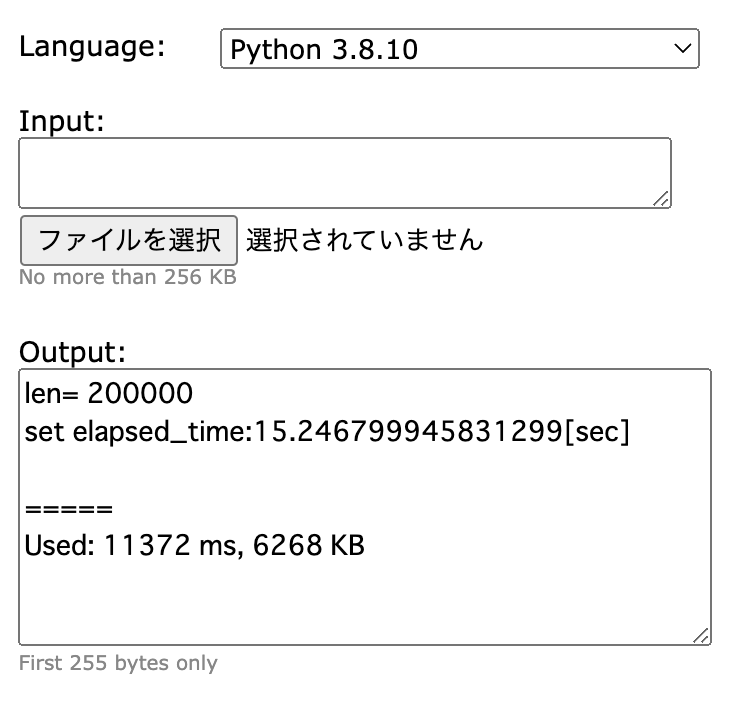
Pythonは15sec以上かかるのにPyPyでは50msもかからずに終了しています。PyPyのソースコードからobjspace/std/setobject.pyを見ます。
class AbstractUnwrappedSetStrategy(object):
def add(self, w_set, w_key):
if self.is_correct_type(w_key):
d = self.unerase(w_set.sstorage)
d[self.unwrap(w_key)] = None
PythonはRPythonで解釈されるので見慣れない関数やメンバですがd = self.uneraseはfrom rpython.rlib import rerasedされており、setobject.pyの
def newset(space):
print("newset()")
return r_dict(space.eq_w, space.hash_w, force_non_null=True)
で確保されたsstorageを読み出し、最終的にはfrom rpython.rlib.objectmodel import r_dictより、rpython/rtyper/lltypesystem/rdict.pyのrdictデータ型です。rdictの実装を読むと
# ------- a port of CPython's dictobject.c's lookdict implementation -------
perturb = r_uint(hash)
while 1:
i = (i << 2) + i + perturb + 1
i = i & mask
checkingkey = entries[i].key
if direct_compare and checkingkey == key:# これは見つかった時の例
return i
perturb >>= PERTURB_SHIFT
であり結果として、Pythonのdictと同じロジック(二重ハッシュのみ)でdictの候補indを計算していることがわかりました。ではdictと同じ入力をsetに$2e5$個入れれば良さそうです。
n = 200000
mask = (1<<17) - 1 # 0xffff
fill = int((1<<15)*1.3+1) # 43599
fill = 40000
arr = [mask+2]
x = 6 # magic number
for i in range(1,fill):
arr += [x]
x = (x * 5 + 1) & mask
arr += [1]*(n-len(arr))
d = set()
for x in arr: d.add(x)


やった!PyPyで十分に時間がかかるsetのanti-set入力を作れました!
このhackケースを防ぐにはどうすればいいですか?
xorを取る(おすすめ)
早いです。戻すのも楽です。
for x in arr: d.add(x) # 3602 ms
->
for x in arr: d.add(x^100) # 46 ms
文字列にする(遅い)
for x in arr: d.add(x) # 3602 ms
->
for x in arr: d.add(str(x)) # 61 ms
sort(不確実)
防げることがあります。targetとする入力を十分な数に積み込む前に入力すれば、定数倍を小さくできるかもしれません。ただし入力によるかもしれません。
for x in arr: d.add(x) # 3602 ms
->
for x in sorted(arr): d.add(x) # 62 ms
余談: なぜPyPyのsetは二重ハッシュ+線形探針を利用している?
setobject.cの頭に書いてあります。
To improve cache locality, each probe inspects a series of consecutive nearby entries before moving on to probes elsewhere in memory. This leaves us with a hybrid of linear probing and randomized probing. The linear probing reduces the cost of hash collisions because consecutive memory accesses tend to be much cheaper than scattered probes. After LINEAR_PROBES steps, we then use more of the upper bits from the hash value and apply a simple linear congruential random number generator. This helps break-up long chains of collisions.
(略)
Use cases for sets differ considerably from dictionaries where looked-up keys are more likely to be present. In contrast, sets are primarily about membership testing where the presence of an element is not known in advance. Accordingly, the set implementation needs to optimize for both the found and not-found case.
キャッシュを効率的に聞かせるために、ランダムプローブの前に連続した線形探査機を行う。連続空間のアクセスはアクセスコストが低い。なぜそうするかというと、辞書(dict)は存在する可能性が高いアクセスに使われることが多いが、集合(set)は存在するかがわからない対象に対して使われることがある。setの実装は存在することが多いような使い方にも、存在しないことが多い使い方にも最適である必要がある。
余談: もっと知りたい!
もっと詳しく!はsetobject.cの頭の通りKnuth先生の本を読みましょう。
The basic lookup function used by all operations. This is based on Algorithm D from Knuth Vol. 3, Sec. 6.4.
