ここでは、無向グラフを考えます。
連結グラフから
1つの辺を取り除くと非連結グラフになるとき、その辺は橋(bridge)と呼ばれます
1つの点を取り除くと非連結グラフになるとき、その点は関節点(articulation point)と呼ばれます。
この橋/関節点を探すアルゴリズムに lowlink があります。
lowlink ではグラフの各点に、2種類の番号付けを行います。
訪問順の番号付け (ord)
1つは、深さ優先探索(dfs)を行って訪問順につけた番号です。(これをord配列に記録することにします)
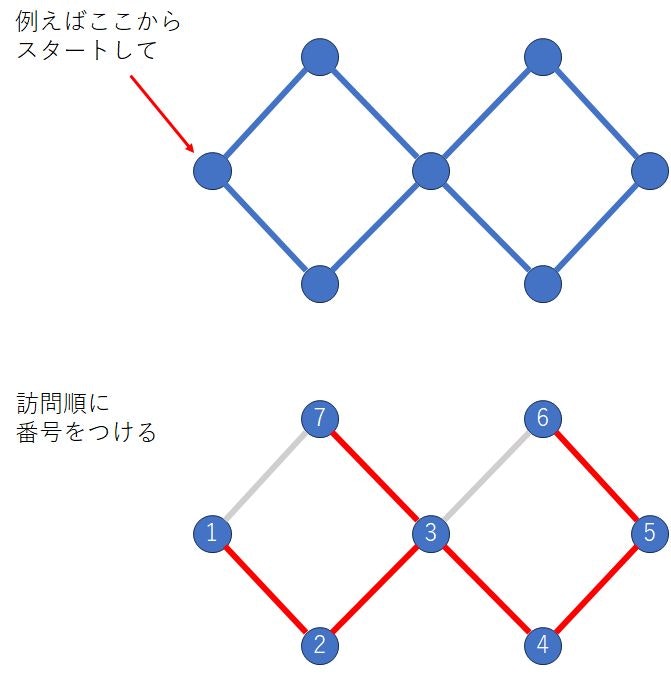
深さ優先探索のときに通過した辺だけで作られるグラフは木になります。
木では、
どの辺を取り除いてもグラフは2つに分かれるので、すべての辺は橋です。
次数が1の点は取り除いてもグラフは連結したままですが、次数が2以上の点は、取り除くとその次数個のグラフに分かれるため関節点です。
閉路の最小値の番号付け (low)
木に使われなかった辺は、深さ優先探索のときに相手先がすでに訪問済みの辺で、この辺を木に追加すると閉路ができます。
深さ優先探索では、これ以上進むことができなくなったときに戻って別の枝に進むため、追加する辺が枝分かれした2つの枝を結ぶことはありません。追加する辺は、ある点と、そこからルート(根)の方向にさかのぼった点(直接の祖先)とを結びます。これを後退辺と呼びます。

low 配列は、最初 ord 配列と同じ値を設定します。
深さ優先探索の行きがけのときに後退辺が見つかると、その相手先の点の ord の値が自分の low の値より小さければ、その ord の値を自分の low の値にします。
深さ優先探索の帰りがけのときに、子の low の値が自分の low の値より小さければ、子の low の値を自分の low の値にします。

このように求めた low には、
・ 閉路を構成する点でない場合は ord と同じ値
・ 閉路の一員の場合は、閉路を構成する点の中で一番小さな ord の値
が設定されることになります。
橋の判定
木ではすべての辺が橋でしたが、閉路(ループ)があるグラフでは、その閉路内の一つの辺を取り除いてもグラフは連結したままです。橋になるのは閉路に含まれない辺です。
注目する辺の両端の点のうち根(ルート) に近いほうを U, 遠いほうを V とします。深さ優先探索の到達順序では、
ord[U] < ord[V]
の関係になります。「U または U より根に近い点」と、「V または V より根から遠い点」とを結ぶ後退辺が存在する場合に限り、この辺は閉路内になります。U,V が閉路内の点のとき、low[U], low[V] はその閉路を構成する点の ord の最小値またはそれより小さい値になるため、
low[V] <= ord[U] < ord[V]
が成り立ちます。このとき辺は閉路内のため橋になりません。
これとは逆に、
ord[U] < low[V]
となる辺は、閉路には含まれないため橋になります。
つまり、根に近いほうの点の ord の値より、根から遠いほうの点の low の値が大きければ橋と判定できます。
関節点の判定
まず、次数が 1 の点は取り除いても連結グラフが非連結になることはありません。
そのため、子を持たない点と、ルートの次数が1の場合のルート点は関節点ではありません。
ルートの次数が2以上の場合、ルート点を取り除くとその次数個のグラフに分かれるため関節点です。
ルート以外では、注目している点をU, その子を V とします。
ord[U] < low[V]
であれば U,V を結ぶ辺を取り除くと非連結になるため、U は関節点です。
また、
ord[U] = low[V]
となるケースでは、U,V は閉路内の点ですが、閉路内で一番ルートに近い点が U であり、U を取り除くと閉路だった部分と U の親との連結が失われて非連結になるため U は関節点です。
以上をまとめると、
ord[U] <= low[V]
となる点Uは関節点になります。
ord[U] > low[V]
の場合は、親 U よりもルートに近い点を含んだ閉路のケースになるので、U を取り除いても 子V と U の親側との連結性は失われません。
関節点を取り除いたときに何個のグラフに分かれるのかを調べたいときは点U と子を結ぶ各辺 (ただし、後退辺は除く) について
ord[U] <= low[V]
がいくつの辺で成り立つかをカウントすれば、元のグラフと合わせて、(1 + カウント数) の個数のグラフに分かれることがわかります。