フェルマーの小定理
$p$ が素数で、$a$ が $p$ の倍数でない自然数のとき
a^{p-1} \equiv 1 \pmod p
が成り立ちます。
$a$ が $p$ の倍数のときは、 $a^m \equiv 0 \pmod p (mは任意の自然数)$ です。
位数
a^{k} \equiv 1 \pmod p
が成り立つ最小の自然数 $k$ は $\mod p$ における $a$ の位数と呼ばれます。
$p-1$ を 位数 $k$ で割ったときの商を $q$, 余りを$ r ( 0 \leqq r < k) $ とすると、
a^{p-1} = a^{qk+r}=(a^k)^q \cdot a^r \equiv 1^q \cdot a^r\equiv a^r\pmod p \\
より $a^{p-1} \equiv a^r \equiv 1 \pmod p$ となりますが、$r$ は位数$k$ より小さいので、位数の定義から$r$ が自然数 ($0<r<k$) であれば $a^r \not\equiv 1 \pmod p$ であり式を満たしません。そのため$r=0$ 、つまり$p-1$は$k$で割り切れる、逆に言うと、$k$ は$p-1$の約数でなければなりません。
ここで、$a$ の位数が$k$ のとき、$(a^{s})^k \equiv (a^k)^s \equiv 1^s \equiv 1 \pmod p (sは自然数)$ であるため、$a^1, a^2, \cdots , a^{k-1} \pmod p$ (これらは互いに相異なる) の位数は $k$ か $k$ の約数です。
位数の求め方
$p-1$ を素因数分解したら $p-1= p_1^{e_1} \cdot p_2^{e_2} \cdots p_n^{e_n} (p_i は素数、e_i > 0)$ になるとします。$a$の位数$k$は$p-1$の約数だから $k= p_1^{k_1} \cdot p_2^{k_2} \cdots p_n^{k_n} (0\le k_i \le e_i)$ の形で表せます。
$p-1=M$とおきます。まず$a^M\equiv 1 \pmod p$ は成立します。
ここで、$M/p_1, M/p_1^2, M/p_1^3 ,\cdots $ について $a^{M/p_1^i}\equiv 1 \pmod p$ が成り立つか計算して確かめます。成り立たなくなるのは、$p_1$の指数が$k_1$より小さくなる場合です。
$a^{M/p_1^i}\equiv 1 \pmod p$ まで成り立ち、$a^{M/p_1^{i+1}}\not\equiv 1 \pmod p$ で成り立たなくなる場合、$k_1=e_1-i$ と指数が確定します。
これを $p_2, \cdots,p_n$ に繰り返せば 位数$k$が確定します。
具体例
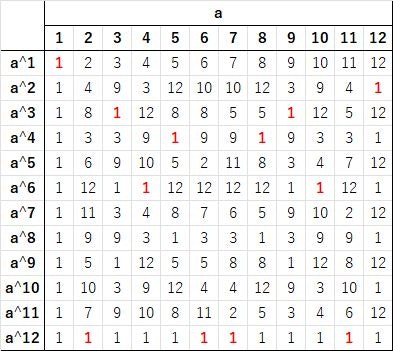
$p=13$ で調べてみます。以下$\mod 13$ を省略します。
$p-1=12=2^2\cdot 3$ と素因数分解できます。
$a^{12/2} =a^6\equiv 1$ となるのは$a=1,3,4,9,10,12$ の6つです。
残りの $a=2,5,6,7,8,11$ の位数は $2^2 \cdot 3^k$ の形になります。
$a^{12/4} = a^3 \equiv 1$となるのは $a=1,3,9$ です。そのため
$a=4,10,12$ は$2^1\cdot 3^k$,
$a=1,3,9$ は $2^0 \cdot 3^k$ の形にないります。
続いて、$a^{12/3} =a^4\equiv 1$ となるのは$a=1,5,8,12$ の4つです。
$a=2,3,4,6,7,9,10,11$ は$3^k = 3^1$
$a=1,5,8,12$ は$3^k = 3^0$ となります。
以上から、1~12の位数はそれぞれ $1,12,3,6,4,12,12,4,3,6,12,2$ と決まります。
もう少し見てみると、$a^2$ の行に出てくる値 $1,4,9,3,12,10$ の位数は $\frac{12}{2}=6$ の約数になっていて、
$a^3$ の行に出てくる値 $1,8,12,5$ の位数は $\frac{12}{3}=4$ の約数になっていて、
$a^4$ の行に出てくる値 $1,3,9$ の位数は $\frac{12}{4}=3$ の約数になっていて、
$a^6$ の行に出てくる値 $1,12$ の位数は $\frac{12}{6}=2$ の約数になっています。
$a^2$ の行に出てくる値 $1,4,9,3,12,10$ は、位数が6 の4,10 の列を縦方向に見たときにあらわれる値です。
$a^3$ の行に出てくる値 $1,8,12,5$ は、位数が4の5,8 の列を縦方向に見たときにあらわれる値です。
$a^4$ の行に出てくる値 $1,3,9$ は、位数が3の3,9 の列を縦方向に見たときにあらわれる値です。
$a^6$ の行に出てくる値 $1,12$ は、位数が2の12 の列を縦方向に見たときにあらわれる値です。
問題にもどって
$A_i^k\equiv A_j \pmod P$ となる $k$ が存在するかが問題となります。
$A_i \equiv 0 \pmod P$ の場合 $A_j \equiv 0 \pmod P$ であれば存在し、$A_j \not\equiv 0 \pmod P$ であれば存在しません。(問題の制約条件から$A_i \equiv 0 \pmod P$ は除外されているので、このケースは考えなくてよいです)
$A_i$ の位数が $P-1$の場合、$A_i^1, A_i^2, \cdots , A_i^{P-1} \pmod P$ に 1から$P-1$ までが1回ずつあらわれるため $A_j \not\equiv 0 \pmod P$ であれば条件を満たす $k$ が存在します。
$A_i$ の位数$k_i$ が $P-1$ より小さい場合、$A_i^1, A_i^2, \cdots , A_i^{P-1} \pmod P$ には$k_i$ 種類の値しか登場しません。$A_j$ がこの中に含まれるのであれば条件を満たす$k$が存在し、含まれない場合は存在しません。
$A_j$ が $A_i^1, A_i^2, \cdots , A_i^{P-1} \pmod P$ に含まれるための必要十分条件は、$A_j$ の位数$k_j$ が$k_i$ の約数であることです。
$P=13$の例でみたように、$A_i$ の位数が$k_i$ の約数である値は、$a^{\frac{P-1}{k_i}}$ の行に登場し、約数でない値はその行にありません。$a^{\frac{P-1}{k_i}}$ の行に登場する値のみが$A_i^1, A_i^2, \cdots , A_i^{P-1} \pmod P$ にあらわれます。
したがって、$A_j$の位数$k_j$ が $A_i$ の位数$k_i$ を割り切る場合にのみ
$A_i^k\equiv A_j \pmod P$ となる $k$ が存在することになります。