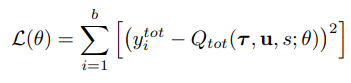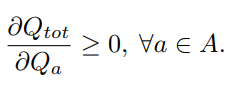COMAレビュー
前回の投稿では、各エージェントのポリシーを評価するための中央制御、すなわち集中型学習(centralized learning)と、チーム報酬を通じて各エージェントの行動に対する報酬評価を行うための報酬整形(reward shaping)を導入したCOMA(Counterfactual Multi-Agent Policy Gradients)について紹介しました。 この手法はアクター・クリティック方式であり、各エージェントはそれぞれアクター(Actor)を持ち、中央にはそれらを統括するクリティック(Critic)が存在していました。
QMIX
今回の投稿では、Q学習の手法を用いて集中型学習(centralized learning)および報酬整形(reward shaping)にアプローチしたQMIXについて紹介したいと思います。 QMIXは、前回取り上げたCOMAと比べてよりシンプルな手法なので、あまり構える必要はないでしょう。 該当論文は以下のリンクから確認できます。
今回も同様に、次のような制約条件があります。
- 1.すべてのエージェントは**部分観測(partial observation)**の情報を用いる。
- 2.各エージェントの部分観測情報は互いに共有されない。
- 3.報酬も個々のエージェントに対してではなく、チーム全体への報酬として与えられる。
このような条件下で、最もシンプルにアプローチしたQ学習手法が、**IQL(Independent Q-Learning, Ming Tan 1993)です。 この手法は、以前の投稿でも述べたように、各エージェントが自身の観測情報のみに基づいて学習します。 そのため、常に安定した性能を発揮できるわけではありませんでした。 今回取り上げるQMIXは、このIQLに集中型学習(centralized learning)**を取り入れた手法です。 以下にQMIXのアーキテクチャを示し、それを通じて説明を続けたいと思います。
$Q_a$ : エージェント $a$ のQ値
$\mathbf{O}_t^a$ : 時刻$t$におけるエージェント $a$ の観測(observation)
$\mathbf{u}_t^a$ : 時刻$t$におけるエージェント $a$ の行動(joint action)
$Q_{\text{tot}}$ : 各エージェントのQ値を統合したもの(全体のQ関数)
まず、図(c)を見ると、各エージェントのアーキテクチャが示されています。 これはCOMAにおける各エージェントのアクターと同じ構造であり、それぞれの部分観測(observation)とjoint-actionを入力としてQ値を出力しています。 このようにして得られたQ値は、図(b)のようにMixing Networkに入力されます。 ここで、このMixing Networkが**集中型学習(centralized learning)**の役割を果たしています。 つまり、各エージェントのQ値とグローバルな状態(state)情報を受け取り、最終的な出力を生成する構造です。 このアルゴリズムがQMIXと呼ばれる理由は、複数のQ値をMixing(混合)しているからです。 こうして得られた$Q_{\text{tot}}$を用いて、次のようなターゲット更新(target update)を行います。 これにより、各エージェントのQ値が評価され、それがReward Shapingの役割を担うことになります。
図(c)は、集中型学習(Centralized Learning)を担うMixing Networkの構造を示しています。 各エージェントのQ値と状態(state)を非線形ニューラルネットワークに適用し、$Q_{\text{tot}}$を最適化します。 ただし、このとき次のような制約条件があります。 それは、Q関数が単調性(Monotonicity)を持っていなければならないということです。 この制約を適用する方法は、単純に絶対値を取って計算するだけで実現できます。 これを数式で表すと、以下のようになります。
上の数式を見ると、$Q_{\text{tot}}$が各エージェントのQ値に関する偏微分であることが分かります。 つまり、これを利用してReward Shapingが行われ、各エージェントのQ値が評価されるのです。
まとめ
QMIXは、従来のIQL手法に集中型学習(centralized learning)とReward Shapingを導入したアルゴリズムです。 集中型学習は、Mixing Network(各エージェントのQ値と状態情報を入力)によって実現され、そこから$Q_{\text{tot}}$が算出されます。 ただし、各エージェントのQ値は単調性(monotonicity)を満たしている必要があります。 最後に、得られた$Q_{\text{tot}}$を用いてReward Shaping、つまり各エージェントのQ値の評価が行われます。 一言で言えば、各エージェントのQ値をニューラルネットワークで統合し、その値を通じて各エージェントを評価する手法です。 そのため、COMAと比べてよりシンプルな方法だと言えるでしょう。
以下のリンクは、QMIXで学習させた結果の映像です。
最初の動画は、他の方がアップロードしたものです。
2つ目は筆者が学習させた結果です。