ベクトルの大きさ
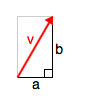
ベクトルの大きさ(長さ)は、三平方の定理(ピタゴラスの定理)を使って求めることができる。また、ベクトルvの大きさは |v| と表記する。
|v| = \sqrt{a² + b²}
ベクトルの向き
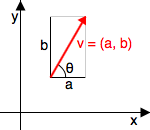
ベクトルv=(a,b)の向きとx軸の正の方向がなす角をθとする。ここで三角関数の定義を思い出して欲しい。三角関数の定義と上図を照らし合わせると、θ,a,bの関係が次式で表せることがわかる。
cos(θ) = \frac{a}{|v|} = \frac{a}{\sqrt{a² + b²}} \\
sin(θ) = \frac{b}{|v|} = \frac{b}{\sqrt{a² + b²}}
三角関数の定義