Pythonを使ったベイズ統計モデリング

頑健線形回帰

統計モデリングにおいて正規分布を仮定するのは一般的な方法です。

しかし、なかには正規分布だとうまく推論できないことがあります。

例えば、外れ値が存在する場合です。外れ値があると、データの統計量が引っ張られてしまい正しい推論ができなくなってしまいます。こうした場合の対処法の一つとして、スチューデントのt分布を使うことがあげられます。

スチューデントのt分布の頑健性を示すために、アンスコムのカルテットデータセットを使います。

アンスコムのカルテット

アンスコムのカルテット(Anscombe's quartet)とは、回帰分析において、散布図はそれぞれ異なるのに回帰直線や統計量が同じになってしまう現象について、統計学者のフランク・アンスコムが紹介した例です。

回帰分析をする前に散布図を確認し、傾向を把握することの重要性や外れ値が統計量に与える影響の大きさを示しています。

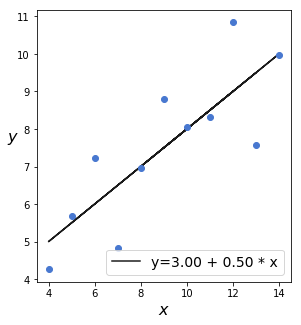
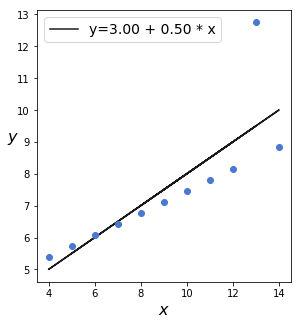
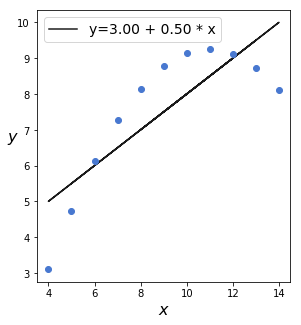
それでは、以下に可視化ライブラリーseabornに入っているアンスコムのカルテットの3例をプロットしてみます。

散布図は異なるのに、回帰式が一致していることがわかります。

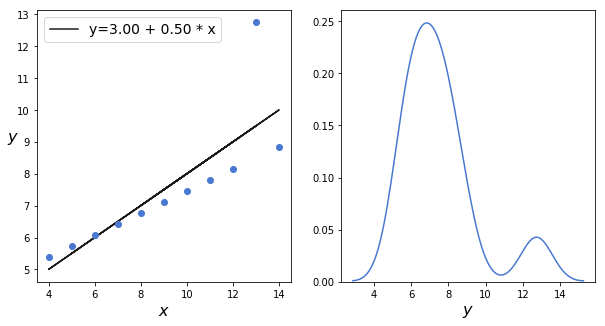
これから、アンスコムのカルテットに含まれる3番目のデータセットを使って、t分布の頑健性を確認していきます。

散布図と回帰直線をプロットしたのち、カーネル密度推定(KDE)します。

# アンスコムのカルテットをロード
ans = sns.load_dataset('anscombe')
# 三番目のデータを取り出す
x_3 = ans[ans.dataset == 'III']['x'].values
y_3 = ans[ans.dataset == 'III']['y'].values

plt.figure(figsize=(10,5))
plt.subplot(1,2,1)

# 回帰分析
beta_c, alpha_c = stats.linregress(x_3, y_3)[:2]

plt.plot(x_3, (alpha_c + beta_c* x_3), 'k', label='y={:.2f} + {:.2f} * x'.format(alpha_c, beta_c))
plt.plot(x_3, y_3, 'bo')
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', rotation=0, fontsize=16)
plt.legend(loc=0, fontsize=14)
plt.subplot(1,2,2)

# カーネル密度推定したものをプロット
sns.kdeplot(y_3)
plt.xlabel('$y$', fontsize=16)

カーネル密度推定したものは、二峰正規分布であることが確認できます。

では、正規分布ではなく、t分布を事前分布に使ったモデルへ書き換えてみます。

t分布を仮定することで、自由度νを特定する必要があります。このνが0に近い値にならないようにするために、シフトした指数分布を使います。ここでいうシフトとは、指数分布をx軸方向に+1することで分布全体を右にずらすことです。

何故そのようなことをするかというと、シフトしていない指数分布は過度の重みをつけて、νを0に近づけてしまうからです。

with pm.Model() as model_t:
    # 各パラメータごとに推論
    alpha = pm.Normal('alpha', mu=0, sd=100)
    beta = pm.Normal('beta', mu=0, sd=1)
    epsilon = pm.HalfCauchy('epsilon', 5)
    nu = pm.Deterministic('nu', pm.Exponential('nu_', 1/29) + 1) # +1してシフトしている
    
    y_pred = pm.StudentT('y_pred', mu=alpha + beta * x_3, sd=epsilon, nu=nu, observed=y_3)
    
    start = pm.find_MAP()
    step = pm.NUTS(scaling=start)
    trace_t = pm.sample(2000, step=step, start=start, njobs=1)
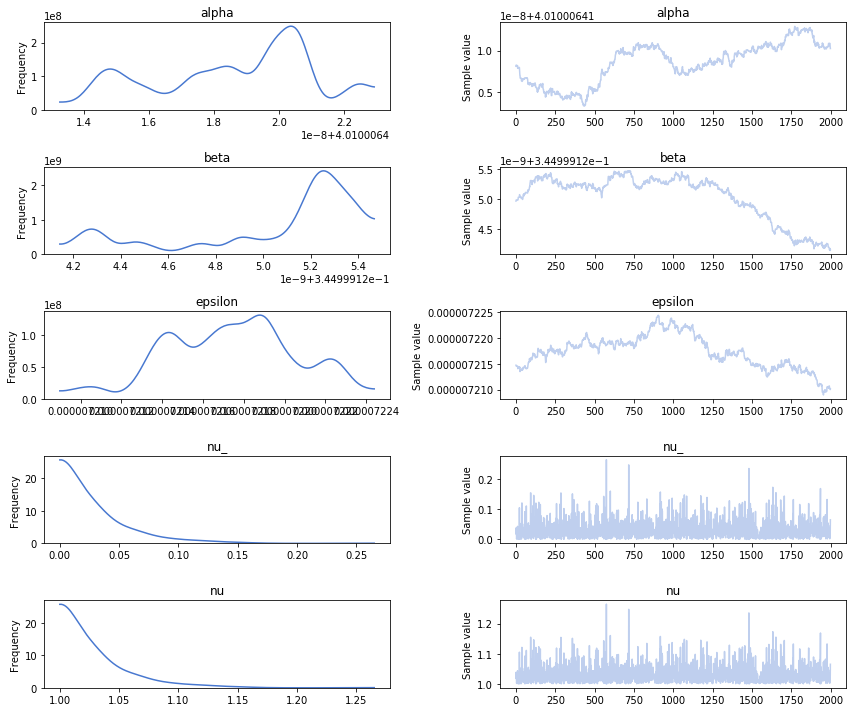
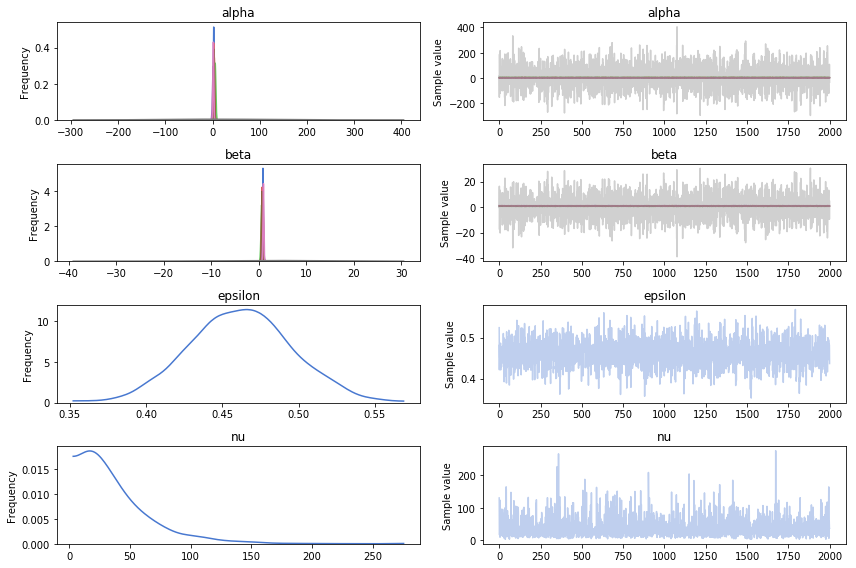
		pm.traceplot(trace_t)

トレースプロットしたものが以下です。

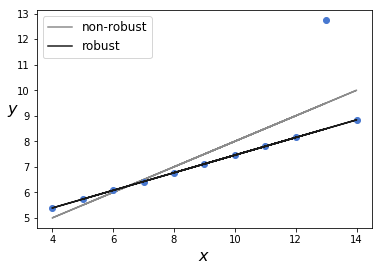
頑健推定された直線と非頑健推定の直線を描きます。

beta_c, alpha_c = stats.linregress(x_3, y_3)[:2]

plt.plot(x_3, (alpha_c + beta_c * x_3), 'k', label='non-robust', alpha=0.5)
plt.plot(x_3, y_3, 'bo')
alpha_m = trace_t['alpha'].mean()
beta_m = trace_t['beta'].mean()
plt.plot(x_3, alpha_m + beta_m * x_3, c='k', label='robust')

plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', rotation=0, fontsize=16)
plt.legend(loc=2, fontsize=12)

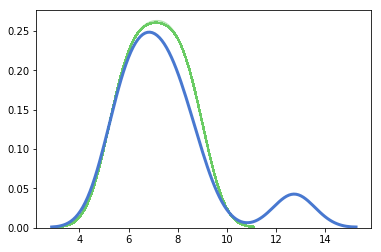
うまく合致しているように見えます。モデルがどれほどうまくデータを捉えているか調べるために、事後予測チェックをおこないます。青が実際のデータで、緑が予測のデータです。

ppc = pm.sample_ppc(trace_t, samples=200, model=model_t, random_seed=2)
for y_tilde in ppc['y_pred']:
    sns.kdeplot(y_tilde, alpha=0.5, c='g')
plt.xlabel('$y$', fontsize=16)
sns.kdeplot(y_3, linewidth=3)

階層線形回帰

階層線形回帰とは、最終的に推定したい回帰式の各パラメータ(例:傾きや切片)のパラメータを推定して組み合わせる線形回帰のことです。

少し詳しく手順を追っていくと、

α + βXで表される回帰式ならば、αとβ、それぞれの事前分布に正規分布を仮定します。

正規分布のパラメータは、μ(平均)、σ(標準偏差)なので、μの事前分布として半コーシー分布、σに正規分布を仮定して…といったように、ハイパーパラメータを推定していきます。

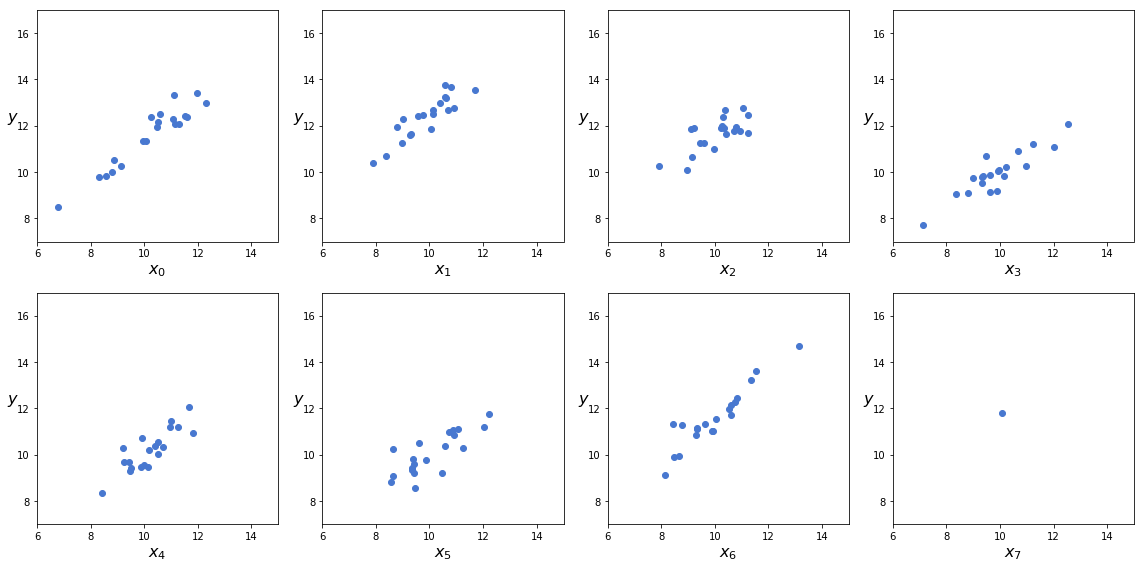
ここでは、データ点が一つしかないグループを含む、8種類のデータグループを作成します。

N = 20
M = 8
idx = np.repeat(range(M-1), N)
idx = np.append(idx, 7)
np.random.seed(314)

alpha_real = np.random.normal(2.5, 0.5, size=M)
beta_real = np.random.beta(6,1,size=M)
eps_real = np.random.normal(0, 0.5, size=len(idx))

y_m = np.zeros(len(idx))
x_m = np.random.normal(10, 1, len(idx))
y_m = alpha_real[idx] + beta_real[idx] * x_m + eps_real

plt.figure(figsize=(16,8))
j, k = 0, N
for i in range(M):
    plt.subplot(2, 4, i+1)
    plt.scatter(x_m[j:k], y_m[j:k])
    plt.xlabel("$x_{}$".format(i), fontsize=16)
    plt.ylabel("$y$", fontsize=16, rotation=0)
    plt.xlim(6, 15)
    plt.ylim(7, 17)
    j += N
    k += N
plt.tight_layout()

作成したデータをモデルに与える前に、データから平均値を引いて中心化します。

それから、非階層モデルにフィットさせます。

x_centered = x_m - x_m.mean()

with pm.Model() as unpooled_model:
    alpha_tmp = pm.Normal('alpha_tmp', mu=0, sd=10, shape=M)
    beta = pm.Normal('beta', mu=0, sd=10, shape=M)
    epsilon = pm.HalfCauchy('epsilon', 5)
    nu = pm.Exponential('nu', 1/30)

    y_pred = pm.StudentT('y_pred', mu= alpha_tmp[idx] + beta[idx] * x_centered, sd=epsilon, nu=nu, observed=y_m)

    alpha = pm.Deterministic('alpha', alpha_tmp - beta * x_m.mean()) 
    
    start = pm.find_MAP()
    step = pm.NUTS(scaling=start)
    trace_up = pm.sample(2000, step=step, start=start, chains=1, cores=4)
    
varnames=['alpha', 'beta', 'epsilon', 'nu']
pm.traceplot(trace_up, varnames)

αとβの分布に広がりがありません。また、νのトレースを見る限りだと、収束していません。

一つしかないデータ点に一意の直線を当てはめることには意味がありません。少なくとも２つの点が必要です。

ここで、αに強い事前分布を使うことで質の良い回帰ができます。

また、階層モデルを定義することでもデータグループ間で情報を共有できるので有益です。

with pm.Model() as hierarchical_model:
    # ハイパー事前分布
    alpha_tmp_mu = pm.Normal('alpha_tmp_mu', mu=0, sd=10)
    alpha_tmp_sd = pm.HalfNormal('alpha_tmp_sd', 10)
    beta_mu = pm.Normal('beta_mu', mu=0, sd=10)
    beta_sd = pm.HalfNormal('beta_sd', sd=10)
    
    # 事前分布
    alpha_tmp = pm.Normal('alpha_tmp', mu=alpha_tmp_mu, sd=alpha_tmp_sd, shape=M)
    beta = pm.Normal('beta', mu=beta_mu, sd=beta_sd, shape=M)
    epsilon = pm.HalfCauchy('epsilon', 5)
    nu = pm.Exponential('nu', 1/30)

    y_pred = pm.StudentT('y_pred', mu=alpha_tmp[idx] + beta[idx] * x_centered, sd=epsilon, nu=nu, observed=y_m)

    alpha = pm.Deterministic('alpha', alpha_tmp - beta * x_m.mean()) 
    alpha_mu = pm.Deterministic('alpha_mu', alpha_tmp_mu - beta_mu * x_m.mean())
    alpha_sd = pm.Deterministic('alpha_sd', alpha_tmp_sd - beta_mu * x_m.mean())
    
    trace_hm = pm.sample(1000, n_jobs=1, chains=1, cores=4)
    
varnames=['alpha', 'alpha_mu', 'alpha_sd', 'beta', 'beta_mu', 'beta_sd', 'epsilon', 'nu']
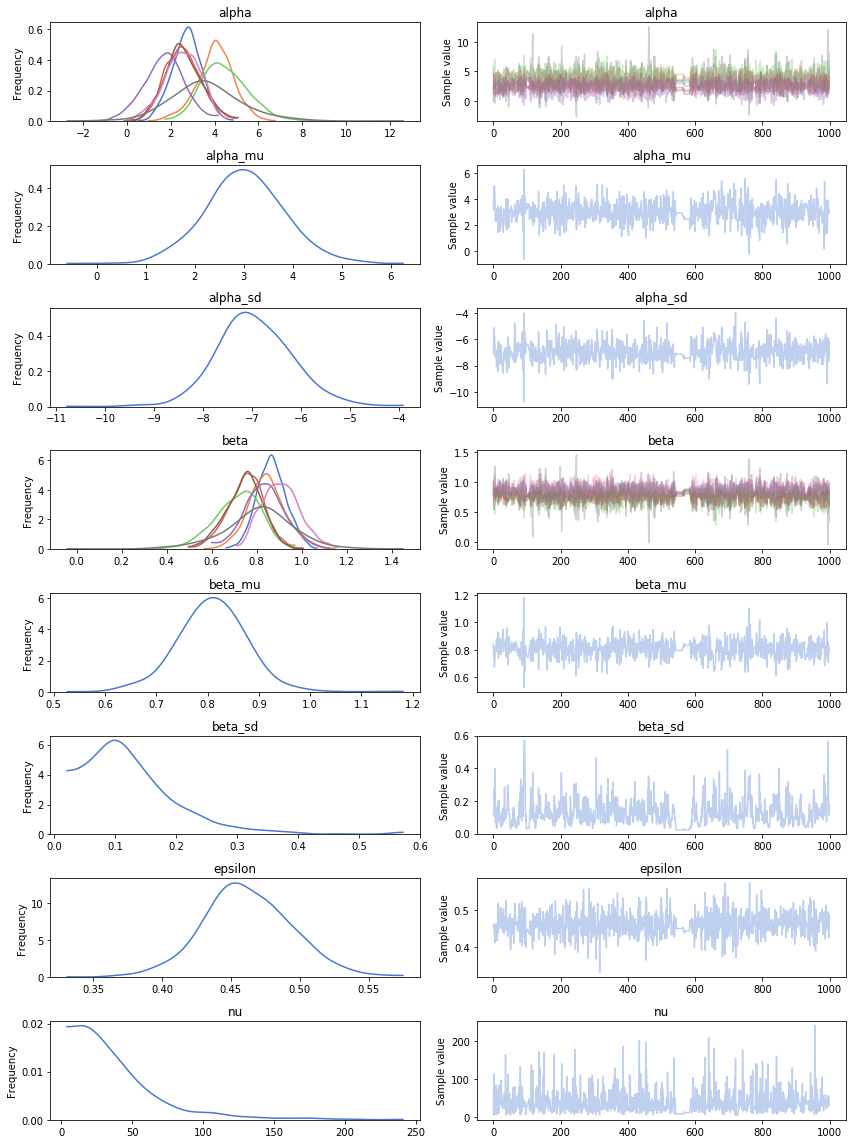
pm.traceplot(trace_hm, varnames)

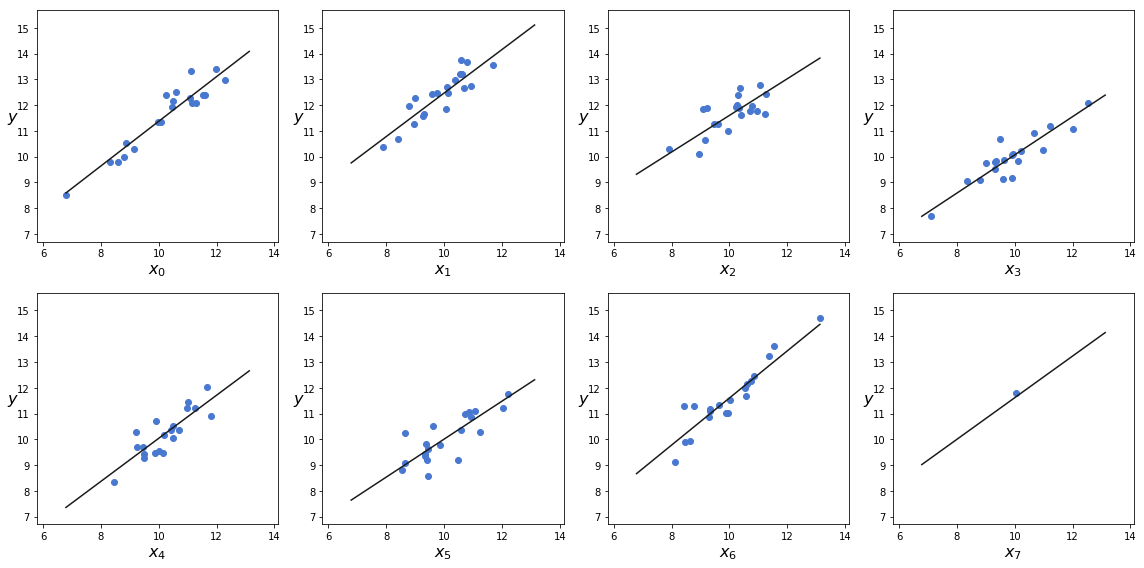
データにフィットさせた直線をグラフ化してみます。

plt.figure(figsize=(16,8))
j, k = 0, N
x_range = np.linspace(x_m.min(), x_m.max(), 10)
for i in range(M):
    plt.subplot(2,4,i+1)
    plt.scatter(x_m[j:k], y_m[j:k])
    plt.xlabel('$x_{}$'.format(i), fontsize=16)
    plt.ylabel('$y$', fontsize=16, rotation=0)
    alfa_m = trace_hm['alpha'][:,i].mean()
    beta_m = trace_hm['beta'][:,i].mean()
    plt.plot(x_range, alfa_m + beta_m * x_range, c='k', label='y = {:.2f} + {:.2f} * x'.format(alfa_m, beta_m))
    plt.xlim(x_m.min()-1, x_m.max()+1)
    plt.ylim(y_m.min()-1, y_m.max()+1)
    j += N
    k += N
plt.tight_layout()

いい感じですね。

多項式回帰

多項式回帰とは、以下のような多項式で表した回帰式のことです。

\mu = \beta_0 x^0 + \beta_1 x^1 + \beta_2 x^2 + \beta_3 x^3 + ... + \beta_n x^n

単純な多項式として、放物線による多項式回帰モデルを構築してみます。

\mu = \beta_0 x^0 + \beta_1 x^1 + \beta_2 x^2

第3項は曲率をコントロールします。

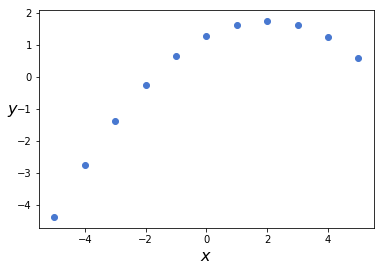
アンスコムの2番目のデータセットを使って多項式回帰してみましょう。

まずは、データをグラフ表示します。

x_2 = ans[ans.dataset == 'II']['x'].values
y_2 = ans[ans.dataset == 'II']['y'].values
x_2 = x_2 - x_2.mean()
y_2 = y_2 - y_2.mean()

plt.scatter(x_2, y_2)
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16, rotation=0)
plt.savefig('B04958_04_21.png', dpi=300, figsize=(5.5, 5.5))

各種パラメータを推定します。

with pm.Model() as model_poly:
    alpha = pm.Normal('alpha', mu=0, sd=10)
    beta1 = pm.Normal('beta1', mu=0, sd=1)
    beta2 = pm.Normal('beta2', mu=0, sd=1)
    epsilon = pm.HalfCauchy('epsilon', 5)

    mu = alpha + beta1 * x_2 + beta2 * x_2**2
    
    y_pred = pm.Normal('y_pred', mu=mu, sd=epsilon, observed=y_2)

    start = pm.find_MAP()
    step = pm.NUTS(scaling=start)
    trace_poly = pm.sample(2000, step=step, start=start, chains=1, cores=4)

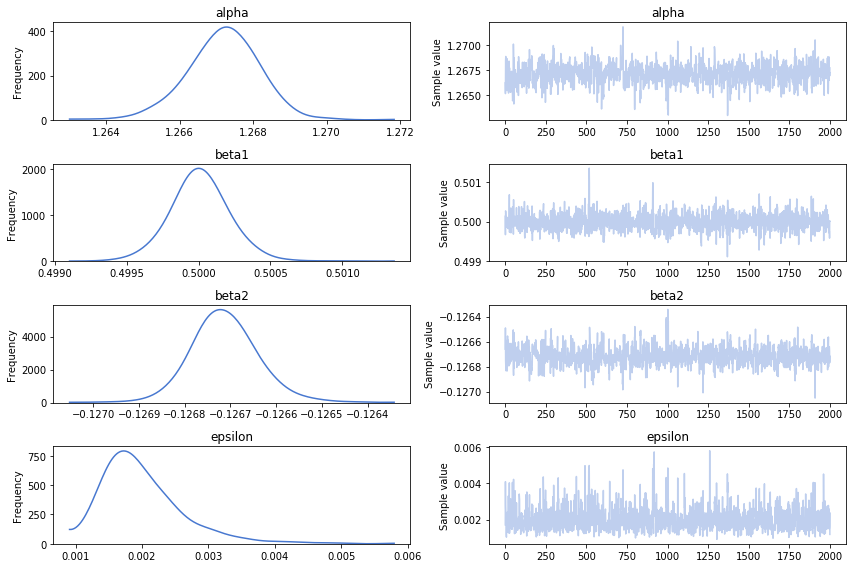
pm.traceplot(trace_poly)

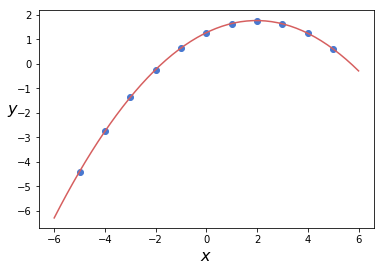
続いて、推定したパラメータを使って多項式回帰をフィッティングしてみます。

x_p = np.linspace(-6, 6)
y_p = trace_poly['alpha'].mean() + trace_poly['beta1'].mean() * x_p + trace_poly['beta2'].mean() * x_p**2
plt.scatter(x_2, y_2)
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16, rotation=0)
plt.plot(x_p, y_p, c='r')

うまく適合しています。

多項式回帰は実用上、3次よりも高いモデルは有益ではありません。
その場合は、他のモデルを探したほうがよいでしょう。

また、これだけうまくフィッティングしていると、多項式回帰はなにかとても素晴らしいものに思えますが、注意が必要です。

データを完全にフィットする多項式を見つけることは常に可能です。ただし、こうして上手くフィットさせるために、過度に複雑なモデルを構築すると、ノイズにもフィットしてしまいます。
過剰にフィットしたモデルは、観測済みデータについてはよく適合しますが、未観測データについては上手く説明できません。
こうした問題を、過剰適合(overfitting)といいます。機械学習や統計モデリングでは度々問題となるので注意しましょう。