はじめに
クォータニオンについての理解を深めるため、クォータニオンについて自分なりに軽くまとめてみました。
筆者は数学には強くないので、間違っているところもあるかもしれません。
間違いを見つけた場合は指摘していただけると助かります。
クォータニオン?
Unityでは クォータニオンは回転を表すものとして使われています。
ちなみにクォータニオンの英語表記はQuaternionです。
クォータニオンの表記
クォータニオンは4つの実数で構成されており、数学では以下のように表記します。
q = [q_x \ q_y \ q_z \ q_w]
$q$がクォータニオン、$q_x, q_y, q_z, q_w$ は実数です.
回転を表すクォータニオン
クォータニオンが以下の等式を満たすとき、クォータニオンは数学的に回転を表すものとなります。
{q_x}^2 + {q_z}^2 + {q_z}^2 + {q_w}^2 = 1
Unityでクォータニオンの長さが1であることを確認してみる
Unityでは Quaternionクラスがクォータニオンに該当します。
Transformクラスの変数rotationはクォータニオンになっています。
Quaternion q = this.transform.rotation;
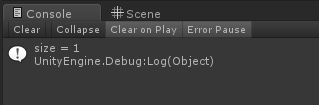
ここで、以下のコードを実行するとクォータニオンの長さの2乗の数値が1になっていることが確認できます。
Quaternion q = this.transform.rotation;
float size = q.x * q.x + q.y * q.y + q.z * q.z + q.w * q.w; // 長さの2乗
Debug.Log("size = " + size);
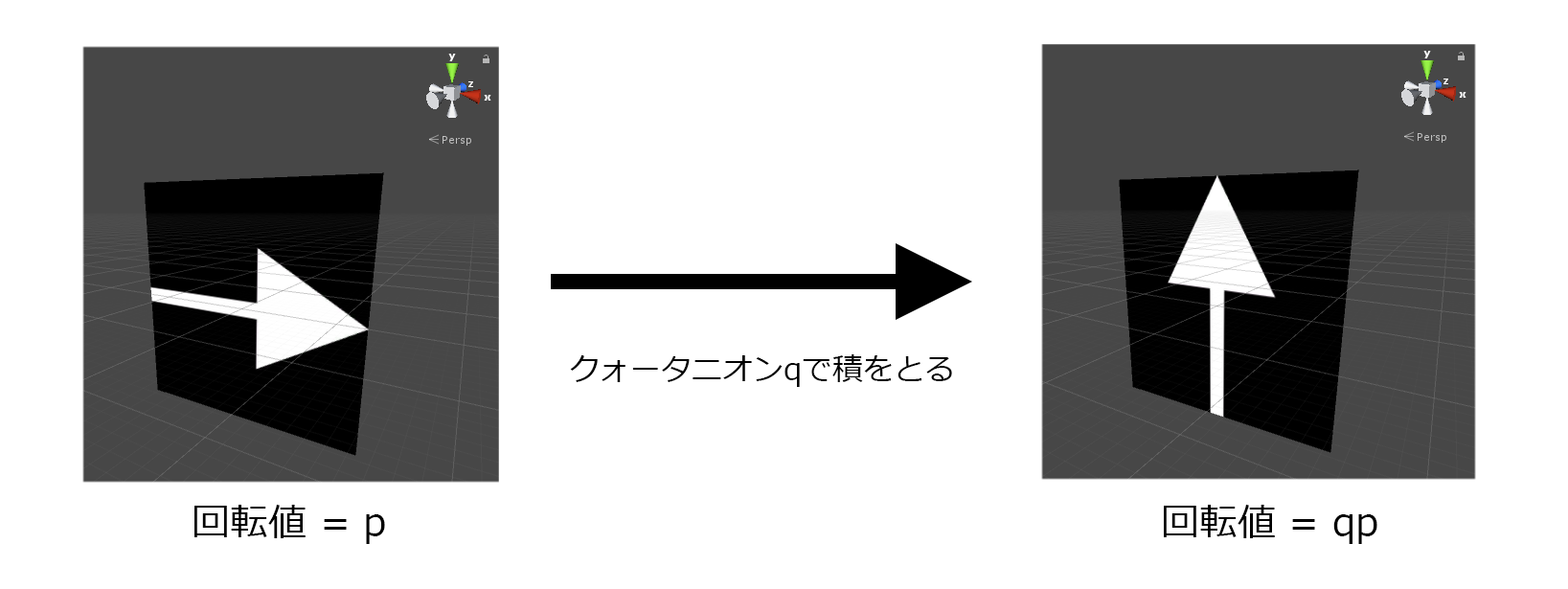
クォータニオンの積
クォータニオン$p$に対してクォータニオン$q$で積をとると、$p$を$q$で回転させるような演算になります。
Quaternion q = Quaternion.Euler(0f, 0f, 90f); // クォータニオン q
this.transform.rotation = q * this.transform.rotation; // 回転
【Unity】オブジェクトをリアルタイムに回転させてみる
クォータニオンを使ってオブジェクトを毎秒90度回転させてみます。
Updateメソッド内で以下のコードを実行します。
Vector3 axis = new Vector3(0f, 0f, 1f); // 回転軸
float angle = 90f * Time.deltaTime; // 回転の角度
Quaternion q = Quaternion.AngleAxis(angle, axis); // 軸axisの周りにangle回転させるクォータニオン
this.transform.rotation = q * this.transform.rotation; // クォータニオンで回転させる

回転の合成
2つのクォータニオンの積をとると回転の合成になります。
Vector3 axis = new Vector3(0f, 0f, 1f); // 回転軸
Quaternion q1 = Quaternion.AngleAxis(+90f * Time.deltaTime, axis); // 毎秒90度回転させるクォータニオン
Quaternion q2 = Quaternion.AngleAxis(-70f * Time.deltaTime, axis); // 反対方向に毎秒70度回転させるクォータニオン
Quaternion q = q1 * q2; // 回転q1と回転q2の合成 (90° - 70° = 20°)
this.transform.rotation = q * this.transform.rotation; // 合成したクォータニオンで回転させる

90°回転のクォータニオンと70°逆回転のクォータニオンを合成しています。

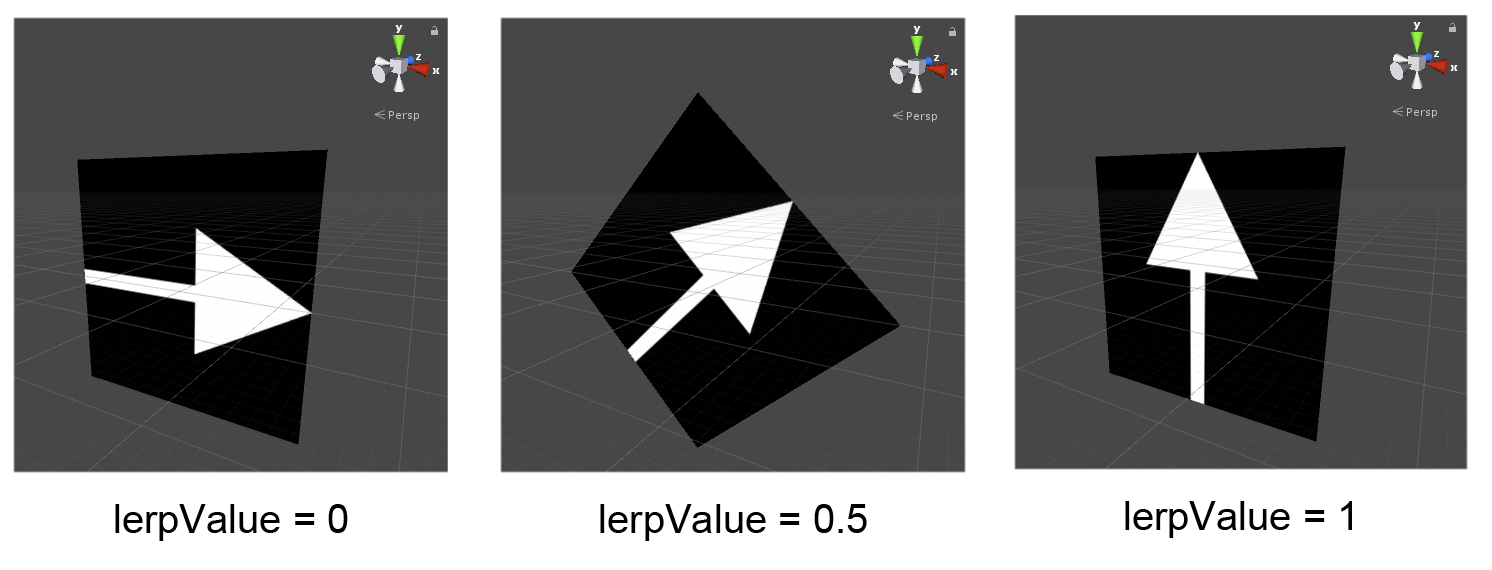
クォータニオンの線形補間
線形補間を利用することで、割合に応じた回転Aと回転Bの中間の値をもとめるといったことが可能になります。
Quaternion q1 = Quaternion.Euler(0f, 0f, 0f); // 回転A
Quaternion q2 = Quaternion.Euler(0f, 0f, 90f); // 回転B
this.transform.rotation = Quaternion.Lerp(q1, q2, lerpValue); // 線形補間
上記コードではlerpValueが割合の数値となっています。
時間で線形補間してみる
以下のコードをMonobehaviourクラスのUpdate内で実行してLerpの挙動を見てみます。
時間を割合の値として線形補間しています
float lerpValue = Time.time;
Quaternion q1 = Quaternion.Euler(0f, 0f, 0f);
Quaternion q2 = Quaternion.Euler(0f, 0f, 90f);
this.transform.rotation = Quaternion.Lerp(q1, q2, lerpValue); // 線形補間
実行すると以下のような挙動になります。

角度(0, 0, 0)からはじまり、時間経過で角度(0, 0, 90)へと近づいていくことが読み取れます。
球面線形補間
クォータニオンには線形補間とは別に球面線形補間というものも存在するそうです。
下記URLで詳しく解説されていました。
https://blogs.msdn.microsoft.com/ito/2009/05/01/963/
Quaternion.Slerpメソッドが球面線形補間になります。
参考書籍
この記事を書くにあたって以下の書籍を参考にさせていただきました。