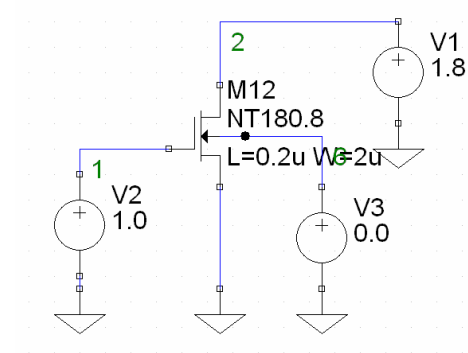
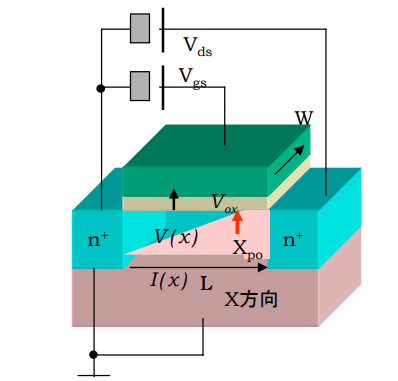
MOSFET 飽和領域・リニア領域の電流式まとめ
- 有効電圧 Veff の定義
Veff = Vgs - VT
条件: Vds > Veff
- 飽和領域の電流式
Ids = (μCox/2)·(W/L)·Veff²·(1 + Vds/VA)
ここで:
μ = キャリア移動度
Cox = 酸化膜容量/面積
W = チャネル幅
L = チャネル長
VA = アーリー電圧 (チャネル長変調を表す)
- トランスコンダクタンス gm
gm = ∂Ids/∂Vgs
= μCox·(W/L)·Veff·(1 + Vds/VA)
近似式 (よく使う形):
gm = 2Ids / Veff
Veff は通常 0.2 V 前後 (0.15~0.3 V 程度) に設定される。
- リニア領域 (トライオード領域, Vds < Veff)
Ids = μCox·(W/L)·(Veff - Vds/2)·Vds
- 飽和領域 (Vds > Veff)
Ids = (μCox/2)·(W/L)·Veff²·(1 + Vds/VA)
解説:
- MOSFET の動作は Vds と Vgs の関係で「リニア領域」と「飽和領域」に分かれる。
- Veff = Vgs - VT は設計の基準電圧で、動作点に応じて 0.15~0.3 V 程度で設定する。
- リニア領域では電流は Vds に比例し、抵抗的に振る舞う。
- 飽和領域では電流は Veff² に比例し、理想的には Vds に依存しないが、実際は VA によるチャネル長変調で Vds にわずかに依存する。
- gm = 2Ids/Veff の関係は回路設計に便利で、Veff を小さくすると高い gm が得られる。
MOSFET のチャネル長変調とドレイン電流式まとめ
- 基本の飽和領域電流
Ids = (μn·Cox / 2)·(W/L)·(Vgs - VTH)²·[1 + λ(Vds - Veff)]
ここで:
μn = 電子移動度
Cox = 酸化膜容量
W = チャネル幅
L = チャネル長
VTH = しきい値電圧
Veff = Vgs - VTH (有効電圧)
λ = チャネル長変調係数
- チャネル長変調係数 λ の式
λ = Kds / (2L√(Vds - Veff) + φ0)
Kds = √(2εsε0 / qNA)
εs = 半導体の誘電率
ε0 = 真空の誘電率
q = 電子電荷
NA = ドーピング濃度
φ0 = ビルトインポテンシャル
→ λ はチャネル長 L に反比例、√(Vds - Veff) にも反比例
- 近似式 (回路設計でよく使う形)
Ids ≈ (μn·Cox / 2)·(W/L)·Veff²·[1 + (Vds / VA)]
VA ≈ 1/λ (アーリー電圧)
- リニア領域電流式 (Vds < Veff)
Ids = μCox·(W/L)·(Veff - Vds/2)·Vds
- 出力コンダクタンス gds
gds = ∂Ids/∂Vds = μCox·(W/L)(Veff - Vds)
特に Vds=0 のとき:
gds|Vds=0 = μCox·(W/L)·Veff
- アーリー電圧 VA の定義
VA ≡ Ids / gds
式展開すると:
VA = [(Veff - Vds/2)Vds] / (Veff - Vds)
解説:
- MOSFET の飽和領域では、電流は理論的には Vds に依存しないが、実際には「チャネル長変調」により Vds が大きくなると電流も増加する。
- この影響を表すパラメータが λ、またはアーリー電圧 VA (≈1/λ)。
- L が短いほどチャネル長変調は大きく、出力抵抗が下がる。
- 回路設計では、Ids の近似式に VA を使うと扱いやすい。