承知いたしました。画像の文字起こしを行います。
177
Z_{out} \approx (R_D // (r_1+r_2+g_m r_1 r_2))...(7.48)
ここで、r_1 \gg r_2、かつg_m r_1 \gg r_2とすると、式(7.49)になります。
Z_{out} \approx (R_D // g_m r_1 r_2)...(7.49)
図7.21の回路は出力端子から見て、M$3の経路とM4の経路がV{out}$から並列に見えることになります。よって、出力端子から見たインピーダンスは、式(7.50)になります。
Z{out} \approx (R_D // (r_1 + r_2 + g_m_1 r_1 r_2))...(7.50)
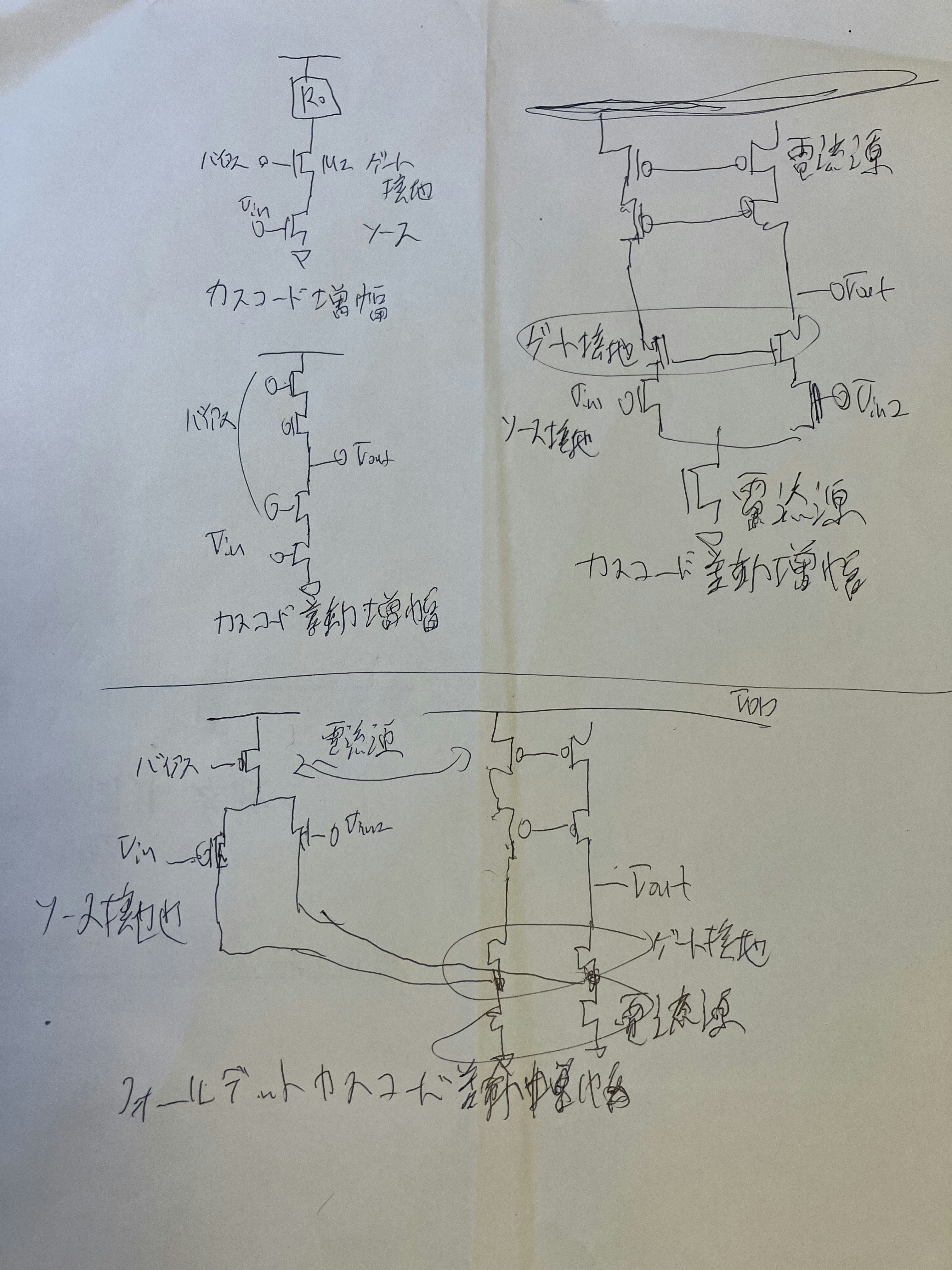
図7.20 カスコード増幅回路
図7.21 カスコード差動増幅回路
178
大きな出力インピーダンスを有することになります。
Z_{out} \approx (g_{m1} r_{o1} // g_{m2} r_{o2})...(7.51)
カスコード回路はトランジスタが縦積みになる構成のため、各トランジスタを飽和動作にバイアスするための必要最低限のドレイン電圧も段数分必要になり、消費電力動産...(文字が切れている)
$V_{GS}-V_{TH} = V_{OD}が必要でした。この構成の場合、各トランジスタのV_{OD}$をあるため、...(文字が切れている)
出力可能範囲が狭くなってしまいます（図7.22）。
●フォールデッド・カスコード差動増幅回路
カスコード回路の出力レンジを広くするために、フォールデッド・カスコード（折り返し型カスコード）回路が用いられます。
図7.22 カスコード差動増幅回路の出力レンジ
179
図7.23の回路は最近のカスコード回路です。M_1とM_2が縦積みになっており、飽和領域で動作するためにV_{DS}$が2つ分積み重ねられてしまいます。この2つのトランジスタを飽和領域にバイアスできれば1つ分$V_{OD}$を減らせます。
このカスコード回路では、$M_1$と$M_2を並列に配置しているので、1つ分V_{OD}$を減らせます。
図7.23のM$1とM$2はNMOSトランジスタからPMOSトランジスタへ変更しているので、...(文字が切れている)
M_1とM_2$の両方がNMOSトランジスタで縦積みされている
図7.23 カスコード回路
180 第7章 応用2 差動増幅回路
インとなり、$V{in}に連動してV{gs}が変動せず、またM{1}はゲートが固定されているのでV{GS}が固定されます。よって信号パスは、図7.23の流れと同じになります。この回路構成により1段分V_{OD}$が節約できるため、出力レンジを広くすることができます（図7.25）。
►小信号解析
図7.26にフォールデッド・カスコード回路の小信号等価回路を示します。この回路の電圧利得を求めます。回路は左右対称のため、ハーフサーキットにて小信号解析を行います。簡単に求めるため、M$5$のドレイン抵抗を無視しています。
少し複雑ですが、$V{in}$、$V_{out}$の線にキルヒホッフの電流則で式を立てて解いていくと、電圧利得が求まります。
まず、V_xでキルヒホッフの電流則を立てると、式(7.51)になります。
-g_{m1} V_{in} + \frac{V_{out}-V_{x}}{r_5} + (-g_{m5} V_{in}) = 0
\frac{V_{out}-V_x}{r_5} = g_{m1} V_{in} + g_{m5} V_{in} = (g_{m1}+g_{m5})V_{in}...(7.51)
181 第7章 応用2 差動増幅回路
次に、V_xでキルヒホッフの電流則を立てると、式(7.52)になります。
V_xでキルヒホッフの電流則を立てると、式(7.52)になります。
(-g_{m1}V_{in}) + (\frac{V_{out}-V_x}{r_5}) + (-g_{m5}V_x) = 0
\frac{V_x-V_{out}}{r_5} - g_{m1}V_{in} - g_{m5}V_x = 0...(7.52)
\frac{V_{out}}{V_{in}} = \frac{g_{m1} g_{m5} r_5 r_6 r_7 + g_{m1} r_6 + g_{m5} r_6 r_7 + 1}{1/r_5 + g_{m1} r_5}
次にキルヒホッフの電流則を立てると、式(7.53)になります。
(\frac{V_{out}-V_{in}}{r_6}) - (-g_{m5} V_x) + \frac{V_{out}}{r_7} + (-g_{m7} V_x) = 0...(7.53)
182 第7章 応用2 差動増幅回路
式(7.53)に式(7.51)と式(7.52)を代入すると、式(7.54)になります。
-g_{m1}V_{in} + (\frac{1}{r_5} + \frac{1}{r_3})V_x + \frac{V_{out}}{r_6} - (\frac{g_{m5}r_3 r_4}{g_{m5}r_3+1}) V_{in}...(7.54)
-(\frac{V_{out}}{r_6} - \frac{V_{in}}{r_6}) - (-g_{m5}V_x) - \frac{V_{out}}{r_7} - (-g_{m7}V_x)=0
(\frac{1}{r_6})V_{out} - (\frac{1}{r_6})V_{in} + g_{m5}V_x - \frac{1}{r_7}V_{out} + g_{m7}V_x = 0
V_x(g_{m5}+g_{m7}) = (\frac{1}{r_6})V_{in} - (\frac{1}{r_6}-\frac{1}{r_7})V_{out}
V_x = \frac{\frac{V_{in}}{r_6} - \frac{r_7-r_6}{r_6 r_7}V_{out}}{g_{m5}+g_{m7}}
V_x = \frac{1}{g_{m5}+g_{m7}} (\frac{V_{in}}{r_6} - \frac{r_7-r_6}{r_6 r_7}V_{out})
-(g_{m1}V_{in})+(\frac{V_{out}-V_x}{r_5}) - g_{m5}V_x = 0
-(g_{m1}V_{in}) + \frac{V_{out}}{r_5} - \frac{V_x}{r_5} - g_{m5}V_x = 0
\frac{V_{out}}{r_5} - g_{m1}V_{in} = V_x(\frac{1}{r_5}+g_{m5})
V_x = \frac{\frac{V_{out}}{r_5} - g_{m1}V_{in}}{\frac{1}{r_5}+g_{m5}} = \frac{V_{out}-r_5g_{m1}V_{in}}{1+r_5g_{m5}}
V_x = \frac{r_6 r_7 g_{m1} + r_5(r_6+r_7)}{r_6 r_7 (1+g_{m5}r_5)}
V_xを消去して整理し、$V_{out}/V_{in}$を求めると式(7.55)になります。
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}(1+g_{m5}r_5)(1+g_{m7}r_7) r_6 r_7}{1+g_{m5}r_5+g_{m7}r_7 + g_{m5}g_{m7}r_5r_7}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_6}{1+g_{m5}r_5} - \frac{g_{m7}}{1+g_{m7}r_7}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1} r_5 r_6 r_7}{r_5 r_6 r_7 + r_5 r_6 r_7 + g_{m5} r_5 r_6 r_7 + r_5 r_6 r_7 g_{m7}}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_5(1+g_{m7}r_7)+r_5 g_{m7} r_7 - r_6 r_7}{r_5(1+g_{m5}r_5)(1+g_{m7}r_7)r_6r_7}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_6(1+g_{m7}r_7)-g_{m5}r_5g_{m7}r_7}{1/r_5+1/r_6+1/r_7+g_{m5}+g_{m7}+g_{m5}r_5+g_{m7}r_7}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_5(1+g_{m7}r_7)(r_6+r_7)+...}{(1+g_{m5}r_5)(1+g_{m7}r_7)}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1} (1+g_{m5}r_5) (1+g_{m7}r_7)}{g_{m1}r_5+g_{m5}r_5+1}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1} r_5 (g_{m5} r_5+1) (g_{m7} r_7+1)}{g_{m1}r_5 (1+g_{m5}r_5) (1+g_{m7}r_7)}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1} r_5}{1+g_{m5} r_5+g_{m7} r_7}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1} r_5 r_6}{g_{m1} r_5 r_6 + g_{m5} r_5 r_6 + r_6 r_7 g_{m7} + r_6 r_7}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_6(g_{m5}r_5+1)+g_{m5}r_5g_{m7}r_7}{1+g_{m5}r_5}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_5 (1+g_{m7}r_7)}{1+g_{m5}r_5}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_6}{g_{m1}r_6(1+g_{m5}r_5)(1+g_{m7}r_7)}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_5 r_6(g_{m7} r_7+1)}{1+g_{m5}r_5+g_{m7}r_7}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}r_5 r_6}{1/r_5+1/r_6+1/r_7+g_{m5}+g_{m7}}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}}{ \frac{1}{r_5}+\frac{1}{r_6}+\frac{1}{r_7} + g_{m5} + g_{m7}}...(7.55)
183 第7章 応用2 差動増幅回路
ここで、右側の式は1となるため、式(7.56)になります。
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}}{ \frac{1}{r_1} + g_{m5} + \frac{1}{r_3} + \frac{1}{r_4} + g_{m7} + \frac{1}{r_6} + \frac{1}{r_7}}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}}{( \frac{1}{r_1} + \frac{1}{r_2} ) + g_{m5}} \frac{1}{( \frac{1}{r_3} + \frac{1}{r_4} ) + g_{m7}}
\frac{V_{out}}{V_{in}} = -g_{m1}(r_1 // r_2) // (r_3 // r_4) // r_5
\frac{V_{out}}{V_{in}} = -g_{m1} (\frac{1}{g_{m5} + 1/r_5} + \frac{1}{g_{m7}+1/r_7})^{-1}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}}{ \frac{1}{r_5} + g_{m5} + \frac{1}{r_7} + g_{m7}}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}}{ \frac{1}{r_5} + g_{m5} + \frac{1}{r_7} + g_{m7}}
$ \frac{V_{out}}{V_{in}} = \frac{-g_{m1}}{ (\frac{1}{g_{m5}r_5+1})\frac{1}{r_5} + (\frac{1}{g_{m7}r_7+1})\frac{1}{r_7} }$
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}(r_5//r_6)(r_7//r_8)}{(g_{m5}r_5+1) + (g_{m7}r_7+1)}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}(r_5//r_6)(r_7//r_8)}{(g_{m5}r_5+1) + (g_{m7}r_7+1)}
\frac{V_{out}}{V_{in}} = \frac{-g_{m1}}{ \frac{1}{r_1 // r_5} + g_{m5} + \frac{1}{r_2 // r_6} + g_{m7} }
Z_{out} \approx (g_{m5}r_5 // g_{m7}r_7)...(7.56)
図7.27 カスコード差動増幅回路の出力インピーダンス