この記事について
ディープラーニングのモデルの予測の不確実性の推定についてMNISTを題材にして実験します。
実験
課題設定
MNIST用に作成したモデルにおいて以下の実現方法を確認します。
- 予測が難しい（推論結果が間違っている可能性が高い）入力データを抽出する
- 訓練外の入力データを抽出する
データ定義
不確実性を測定実験のために以下のデータを使用します。
- mnist (モデル訓練用)
- fashion mnist (訓練外データ用)
モデルをCNNで作成するため、データを28x28x1の形式に変換します。
import keras
import numpy as np
def convert_data(x_train, y_train, x_test, y_test):
# トレーニングデータから検証用データを作成
from sklearn.model_selection import train_test_split
x_train, x_valid, y_train, y_valid = train_test_split(x_train, y_train, test_size=10000)
# 入力データのフォーマットを変換
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
x_train = x_train.astype('float32')
x_train /= 255
x_valid = x_valid.reshape(x_valid.shape[0], 28, 28, 1)
x_valid = x_valid.astype('float32')
x_valid /= 255
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
x_test = x_test.astype('float32')
x_test /= 255
# 出力データをone-hotに変換
y_train = keras.utils.to_categorical(y_train, 10)
y_valid = keras.utils.to_categorical(y_valid, 10)
y_test = keras.utils.to_categorical(y_test, 10)
return (x_train, y_train),(x_test, y_test), (x_valid, y_valid)
# トレーニングデータ、テストデータを取得(mnist, fashion_mnist)
(x_train_m, y_train_m), (x_test_m, y_test_m) = keras.datasets.mnist.load_data()
(x_train_f, y_train_f), (x_test_f, y_test_f) = keras.datasets.fashion_mnist.load_data()
# データを整形
(x_train_m, y_train_m), (x_test_m, y_test_m), (x_valid_m, y_valid_m) = convert_data(x_train_m, y_train_m, x_test_m, y_test_m)
(x_train_f, y_train_f), (x_test_f, y_test_f), (x_valid_f, y_valid_f) = convert_data(x_train_f, y_train_f, x_test_f, y_test_f)
# mnistデータで学習
(x_train, y_train), (x_test, y_test),(x_valid, y_valid) = (x_train_m, y_train_m), (x_test_m, y_test_m), (x_valid_m, y_valid_m)
モデル定義
シンプルなCNNモデルを作成します。MCDropoutの実験を行うため、Dropoutを適用します。
model = keras.models.Sequential()
model.add(keras.layers.Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(keras.layers.Dropout(0.25))
model.add(keras.layers.Flatten())
model.add(keras.layers.Dense(128, activation='relu'))
model.add(keras.layers.Dropout(0.5))
model.add(keras.layers.Dense(10, activation='softmax'))
model.summary()
model.compile( loss='categorical_crossentropy', optimizer=keras.optimizers.RMSprop(), metrics=['accuracy'])
history = model.fit(x_train, y_train,
batch_size=128,
epochs=20,
verbose=1,
validation_data=(x_valid, y_valid))
不確実性の推定
学習したモデルを使って、推論時の不確実性測定の実験を行います。 不確実性の計算には以下を使います。
-
予測全体の不確実性(=偶然の不確実性 + 認識の不確実性)
- softmaxのエントロピー
-
認識の不確実性
- ベイジアンニューラルネットワークの考え方に基づいて測定
- MCDropoutによるsoftmaxの分散
softmaxのエントロピーは正規化エントロピーを用います。（エントロピーの多様性の成分を除去するため）
MCDropoutによるsoftmaxの分散は、出力結果の確率分布と学習した重みパラメータの事後分布の相互情報量の近似値を表します。訓練したことのないデータが入力されると不確実性が高くなります。
通常実行
通常通り分類し、softmax出力の結果に対してエントロピーを計算して不確実性を推定します。エントロピーは多様性成分を除去するために正規化しています。エントロピーの判定閾値は適当に0.005と設定しています。
def show_img(data,row=1,col=20):
plt.figure(figsize=(10,10))
num_of_images = row * col
for i in range(num_of_images):
plt.subplot(row, col, i+1)
plt.imshow(data[i].reshape(28,28), cmap="gray")
plt.axis('off')
def result_create_helper(x, y_correct, num_of_samples, pred_y, uncertainty, th):
# 不確実性の測定値のヒストグラムを表示
plt.hist(uncertainty,bins=100,range=(0,0.01))
plt.xlabel('uncertainty')
plt.ylabel('frequency')
plt.show()
uncertainty_high_data = [] # 不確実性が高いと判定された入力データ
uncertainty_high_predict = [] # 不確実性が高いと判定された入力データに対する予測結果
uncertainty_high_count = 0 # 不確実性が高いと判定された入力群の中で正しく推論できた回数
uncertainty_low_data = [] # 不確実性が低いと判定された入力データ
uncertainty_low_predict = [] # 不確実性が低いと判定された入力データに対する予測結果
uncertainty_low_count = 0 # 不確実性が低いと判定された入力群の中で正しく推論できた回数
# 入力に対する予測結果を１つずつ確認
# 不確実性が高いと判定された入力と低いと判定された入力を場合分け
for i in range(num_of_samples):
correct_plus = 0
predict_num = np.argmax(pred_y[i]) # 予測結果
correct_num = np.argmax(y_correct[i]) # 正解
# 予測結果と正解が等しい場合はカウントアップ
if predict_num == correct_num:
correct_plus = 1
if uncertainty[i] > th:
uncertainty_high_data.append(x[i])
uncertainty_high_predict.append(predict_num)
uncertainty_high_count += correct_plus
else:
uncertainty_low_data.append(x[i])
uncertainty_low_predict.append(predict_num)
uncertainty_low_count += correct_plus
# 出力結果の整形
uncertainty_high_data = np.array(uncertainty_high_data)
uncertainty_high_predict = np.array(uncertainty_high_predict)
uncertainty_high_acc = uncertainty_high_count/len(uncertainty_high_data)
uncertainty_low_data = np.array(uncertainty_low_data)
uncertainty_low_predict = np.array(uncertainty_low_predict)
uncertainty_low_acc = uncertainty_low_count/len(uncertainty_low_data)
# 結果表示
print( "num of high uncertainty={}, acc={:.2f}%".format(len(uncertainty_high_data),uncertainty_high_acc*100) )
print( "predict=", uncertainty_high_predict[:20])
show_img(uncertainty_high_data)
print( "num of low uncertainty={}, acc={:.2f}%".format(len(uncertainty_low_data),uncertainty_low_acc*100) )
print( "predict=", uncertainty_low_predict[:20])
show_img(uncertainty_low_data)
def result_create(x,y_correct):
num_of_samples = len(x)
num_of_classes = len(y_correct)
# softmaxの出力結果
pred_y = model.predict(x)
max_p = np.max(pred_y, axis=1)
# 正規化エントロピーで不確実性を測定
entropy = np.sum(-pred_y*np.log(pred_y)/np.log(num_of_classes),axis=1)
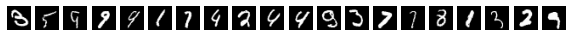
result_create_helper(x,y_correct,num_of_samples,pred_y,entropy,0.005)
# x_test, y_testで不確実性を測定
result_create(x_test, y_test)
出力結果を見ると、エントロピーが高くなる入力データは文字の形状が比較的あいまいなものになっており、本質的に推論が難しいものになっていることが確認できます。また、出力結果のエントロピーが高い入力データのグループの方が推論精度が低下していることが確認できます。
不確実性(正規化エントロピー)の測定値のヒストグラム
予測結果のエントロピーが高くなる入力データ
num of high uncertainty=834, acc=85.61%
predict= [3 5 9 9 9 1 7 4 2 4 4 9 3 7 1 8 1 3 2 9]
予測結果のエントロピーが低くなる入力データ
num of low uncertainty=9166, acc=99.86%
predict= [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5 9 7 4 9]
入力データの一部にノイズを付加
入力データの一部にわざとノイズを付加して推論の不確実性がどのように変化するか確認します。
ノイズがない場合は正しく推論できていた入力データに対して間違った推論結果が出力される場合があることが確認できます。また、その推論結果のエントロピーも増加していることも確認できます。偶発的不確実性に関してはエントロピーの測定も効果が期待できることが示唆されます。
# 一部の入力データにノイズを付加
x_test_r = x_test.copy()
x_test_r[:1000] = 0.3*x_test[:1000] + 0.7*np.random.rand(28,28,1)
result_create(x_test_r, y_test)
不確実性(エントロピー)の測定値のヒストグラム
予測結果のエントロピーが高くなる入力データ
num of high uncertainty=1741, acc=50.32%
predict= [2 2 2 2 2 2 2 8 8 2 2 8 2 8 8 2 2 2 8 2]
予測結果のエントロピーが低くなる入力データ
num of low uncertainty=8259, acc=99.84%
predict= [9 0 2 5 1 9 7 8 1 0 4 1 7 9 5 4 2 6 8 1]
訓練外データの入力
モデルに対して、学習していない訓練外データを入力した結果を確認します。
通常のmnistのデータを入力した時と比較して、エントロピーは高い方に多く分布することが確認できます。エントロピーを測定することで、今回の簡単な閾値判定でも、約92%の訓練外データを検出することができていることが確認できます。
num of high uncertainty=9261, acc=10.38%
num of low uncertainty=739, acc=10.83%