「エントロピーと秩序」のプログラムをpythonで書く～カルノーサイクル

初めに

去年の夏、エントロピーにはまっていていろいろな本を読んでいたのですが、その中の一つに「エントロピーと秩序」という本があります。この本の巻末にBASICで書かれたプログラムがいくつか載っているのですが、BASICの実行環境がないので実行できません。そこで、pythonで書き換えてみることにしました。

カルノーサイクル

ひとつめに載っているプログラムが「カルノーサイクル」です。

import math
import matplotlib.pyplot as plt

plt.xlabel("V")
plt.xticks(color="None")
plt.ylabel("P", rotation=0)
plt.yticks(color="None")

TU = int(input("高温部の温度"))
TL = int(input("低温部の温度"))
Q = int(input("膨張段階で吸収される熱量"))
VI = int(input("初期体積"))

VA = VI  # A点の体積
PA = TU / VA  # Aでの圧力
plt.annotate("A", (VA, PA))

# A-B(等温膨張)
VB = VA * math.exp(Q / TU)  # B点の体積
v = VA
xab = []
yab = []
while(v < VB):
    p = TU / v
    xab.append(v)
    yab.append(p)
    v += 0.1
plt.plot(xab, yab, "g")
PB = p  # B点での圧力
plt.annotate("B", (VB, PB))

# B-C(断熱膨張)
VC = ((PB / TL) * (VB ** 1.667)) ** 1.5  # C点の体積
PC = TL / VC  # C点での圧力
v = VB
xbc = []
ybc = []
while(v < VC):
    p = PB * ((VB / v) ** 1.667)
    xbc.append(v)
    ybc.append(p)
    v += 0.1
plt.plot(xbc, ybc, "y")
plt.annotate("C", (VC, PC))

# C-D(等温圧縮)
VD = ((PA / TL) * (VA ** 1.667)) ** 1.5  # D点の体積
PD = TL / VD  # D点の圧力
v = VC
xcd = []
ycd = []
while(v > VD):
    p = TL / v
    xcd.append(v)
    ycd.append(p)
    v -= 0.1
plt.plot(xcd, ycd, "r")
plt.annotate("D", (VD, PD))

# D-A(断熱圧縮)
xda = []
yda = []
v = VD
while(v > VA):
    p = PA * (VA / v) ** 1.667
    xda.append(v)
    yda.append(p)
    v -= 0.1
plt.plot(xda, yda, "b")
plt.show()

QC = TL * math.log(VC / VD)  # CD間で吸収される熱量
W = Q - QC  # 1サイクルで得られる仕事量
E = W / Q  # 効率

print(f"効率: {E:.2f}")

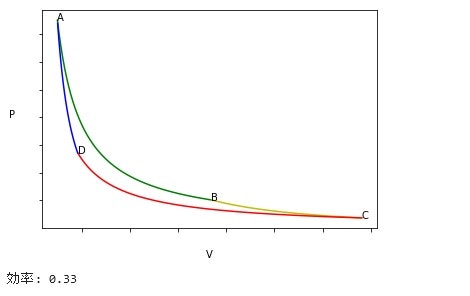
もともとは37行のプログラムだったのですが、書き直すと76行になってしまいました。本に書いてある通り、高温部の温度を1500、低温部の温度を1000、吸収される熱量を3000、初期体積を10で入力すると以下のようなグラフが表示されます。

それっぽいグラフが表示されるので問題なさそうです。
ちなみに、エントロピー系の本をいろいろ読んだ中で、私は「エントロピーと秩序」と「高校数学でわかるボルツマンの原理 : 熱力学と統計力学を理解しよう」が面白かったです。