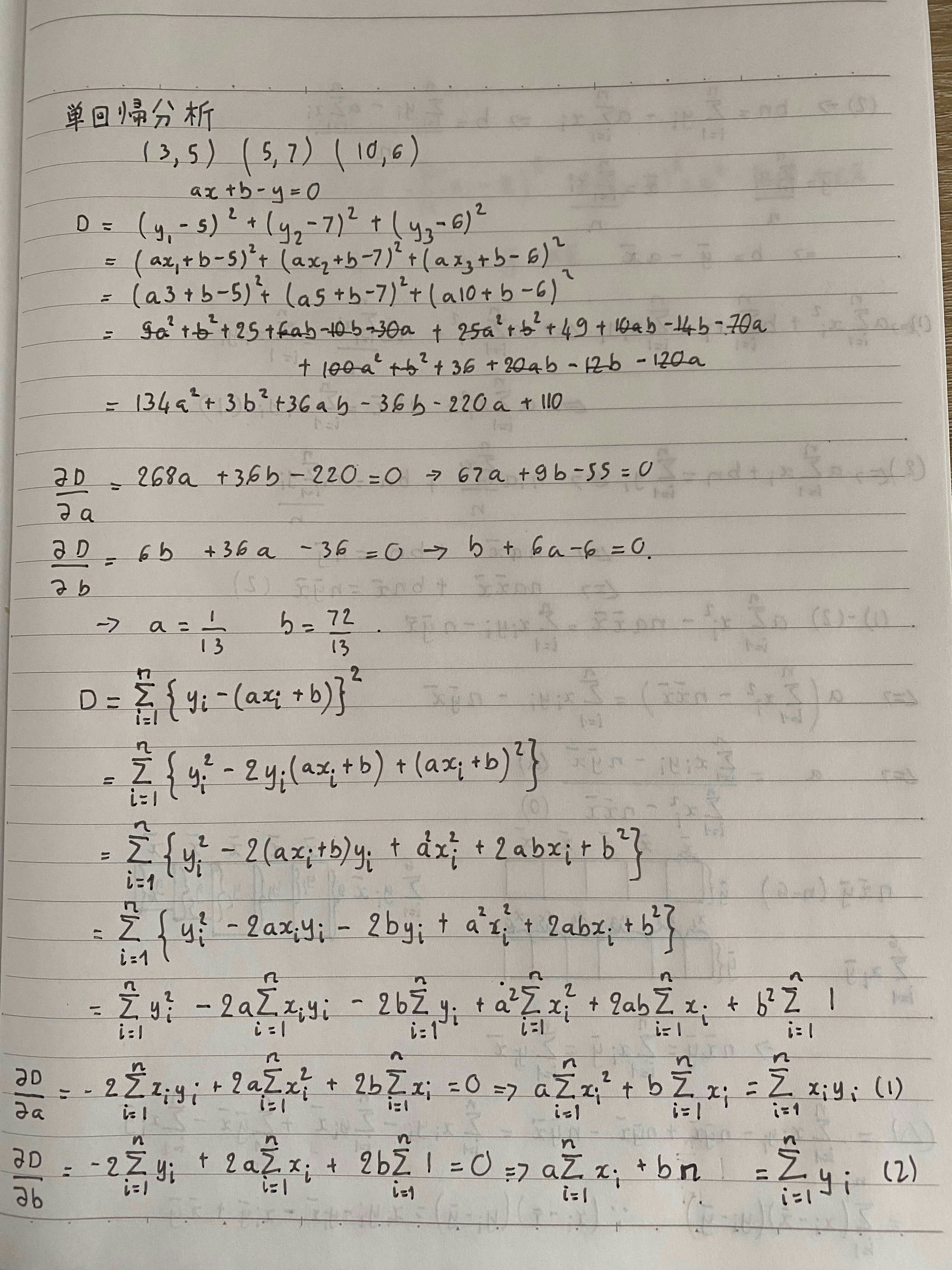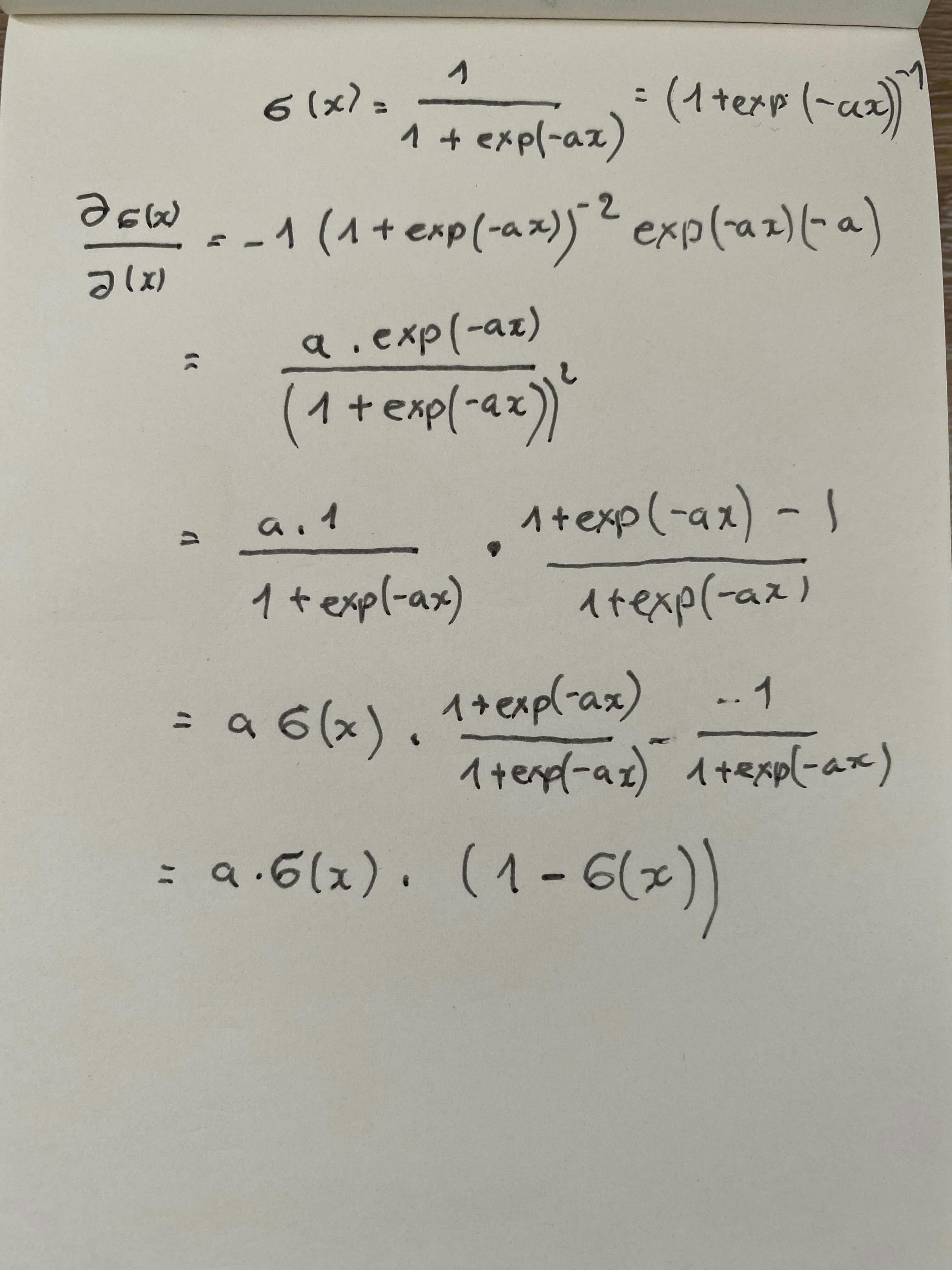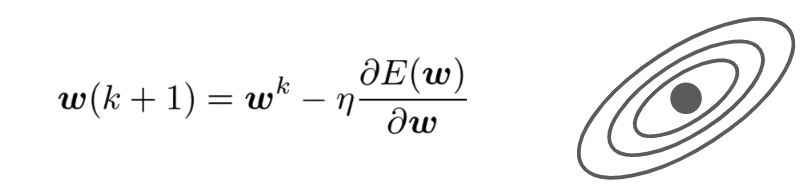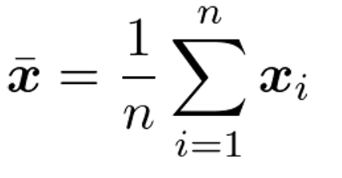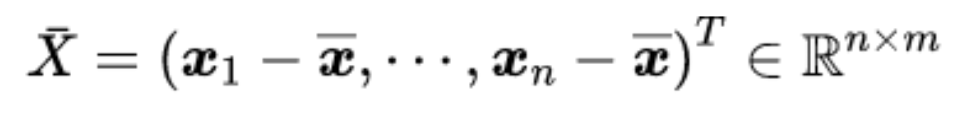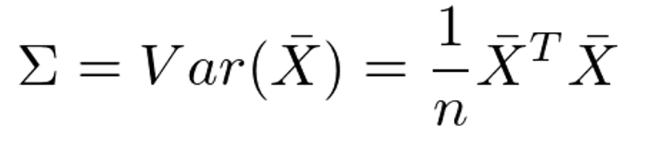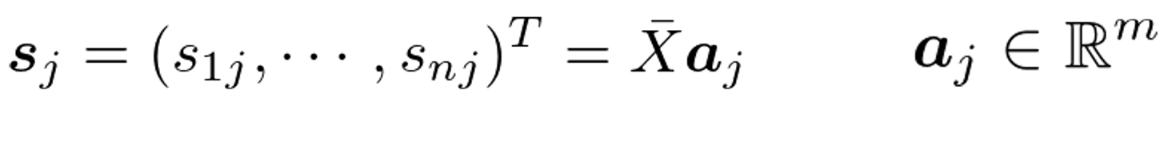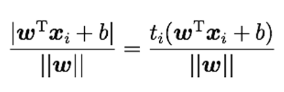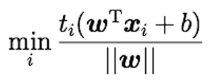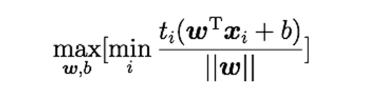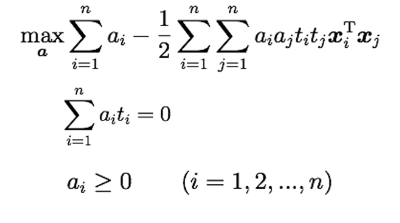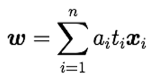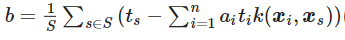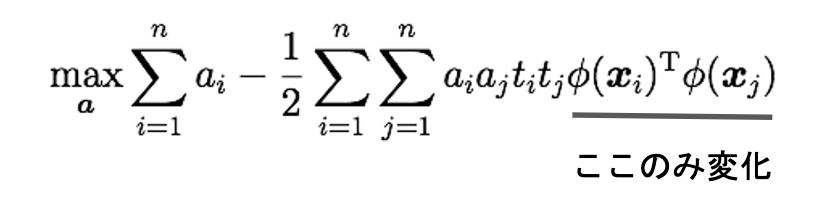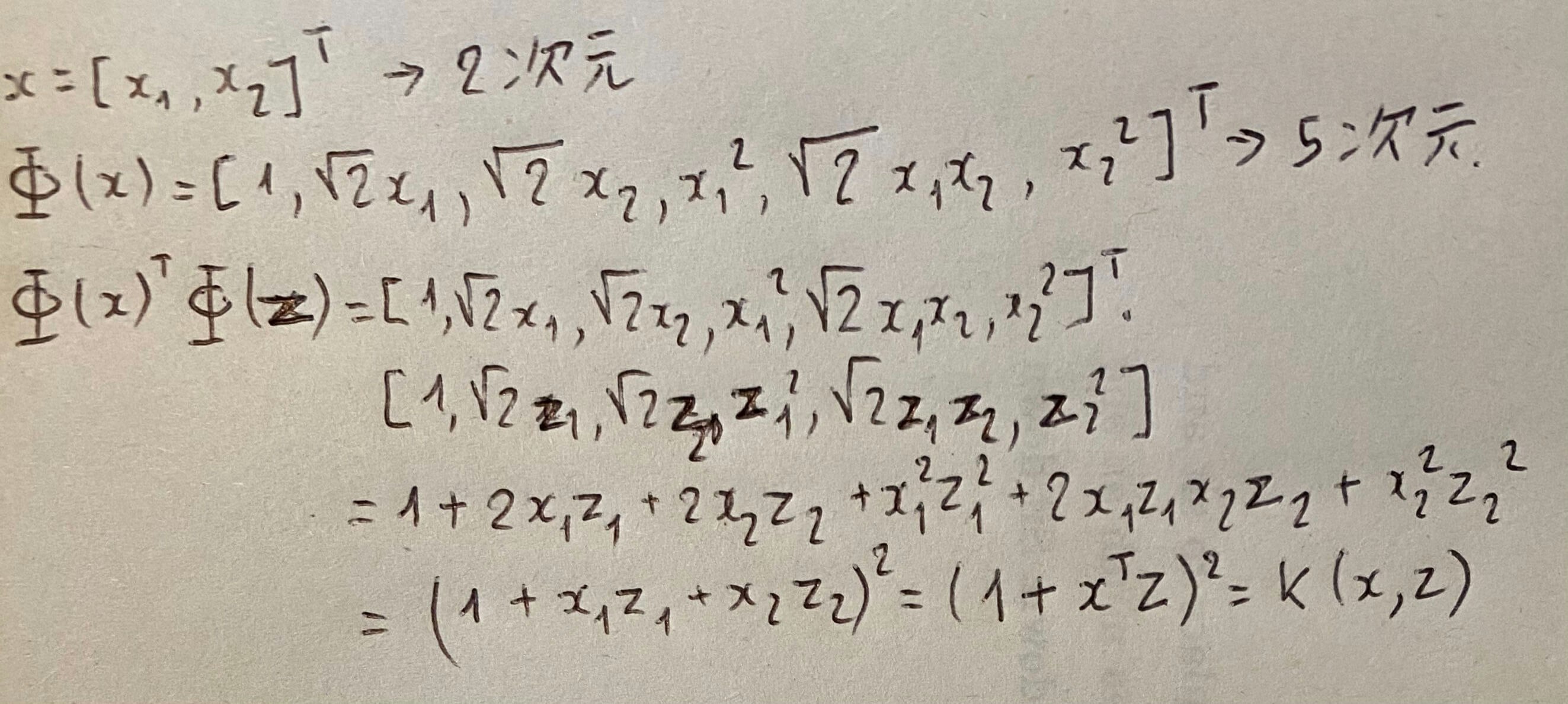機械学習

モデル選択・評価

データの分割

• 学習データ：モデルを学習させるデータ
• 検証データ：学習済みのモデルの精度を検証するためのデータ

何故か
学習済みのモデルの凡化性を測定するため
凡化性：データへ当てはまる良さではなくて、未知のデータへ当てはまる性質

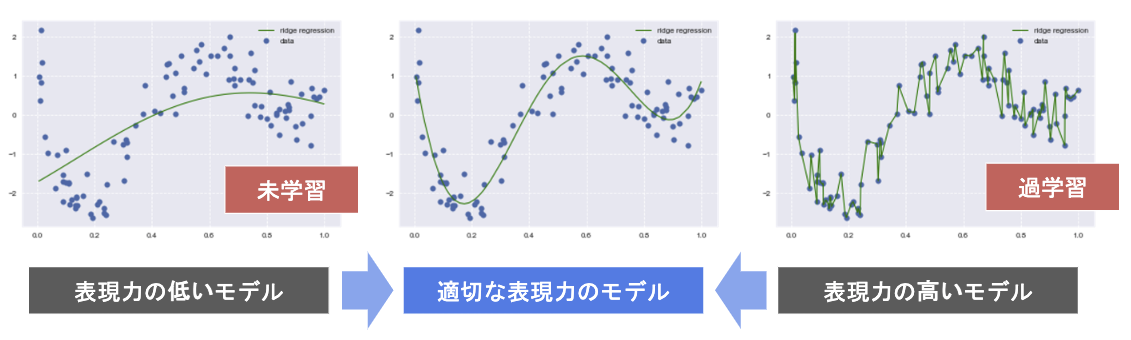
未学習(underfit) ・ 過学習(overfit)

未学習

学習データに対して、十分小さい誤差が得られない
対策：表現力の高いモデルを利用する（学習パラメータ数を増やす）

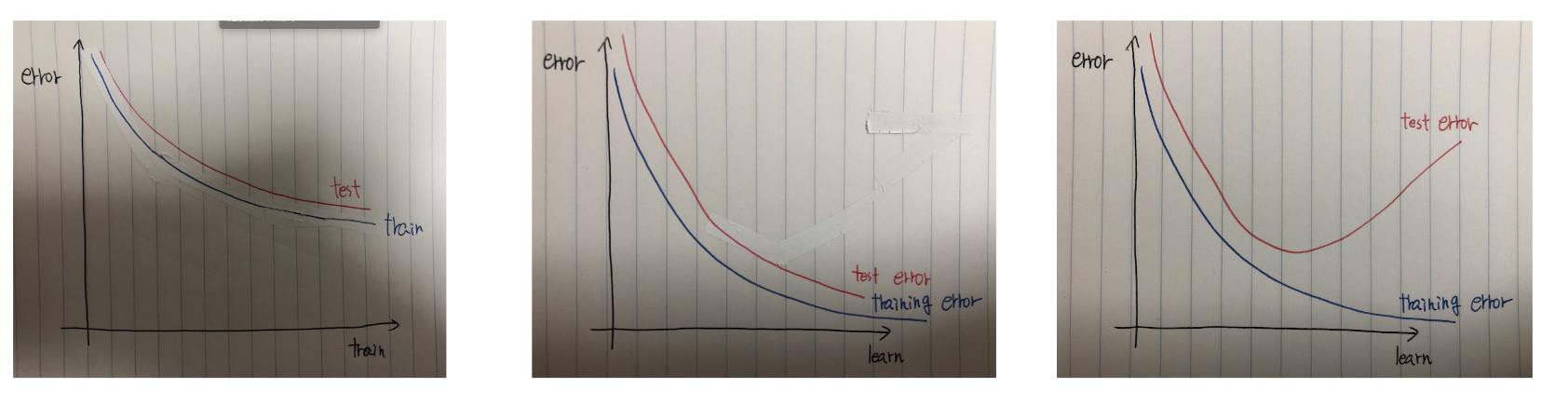
過学習

学習データに対して、十分小さい誤差が得られたが、
検証データの誤差が学習データの誤差の差が大きい
対策①：学習データを増やす
対策②：モデルの表現力を抑止する（学習パラメータ数を減らす）
対策③：正則化法を利用する

正則化法

正則化項（罰則項）

 \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon} \qquad 
\boldsymbol{\beta} = \begin{pmatrix} \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{n} \end{pmatrix} 

回帰

\hat{\boldsymbol{\beta}} = \arg \min \left\{||\mathbf{y} -  \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \right\}

Lasso

||\boldsymbol{\beta}||_{1}^{1} = |\beta_{1}| + |\beta_{2}| + \cdots + |\beta_{n}|\\
\hat{\boldsymbol{\beta}} = \arg \min \left\{ ||\mathbf{y} -  \mathbf{X}\boldsymbol{\beta}||^{2}_{2} + \lambda ||\boldsymbol{\beta}||_{1}^{1}  \right\}

Ridge

||\boldsymbol{\beta}||_{2}^{2} = |\beta_{1}|^{2} + |\beta_{2}|^{2} + \cdots + |\beta_{n}|^{2}\\
\hat{\boldsymbol{\beta}} = \arg \min \left\{ ||\mathbf{y} -  \mathbf{X}\boldsymbol{\beta}||^{2}_{2} + \lambda ||\boldsymbol{\beta}||_{2}^{2}  \right\}

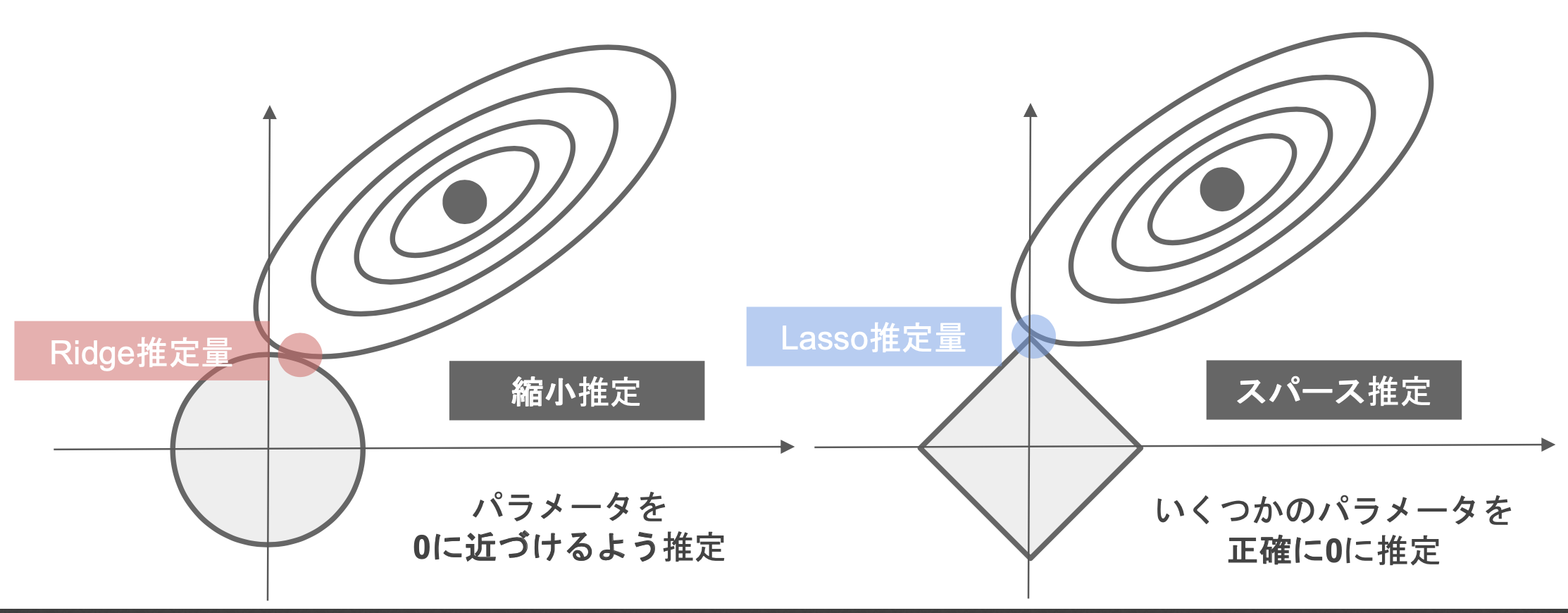
λが小さい→普通の回帰になる
λが大きい→製薬効果が高くなる

参考

ホールドアウト法

データを学習用と検証用の２つに分割する方法
大量のデータが必須

クロスバリデーション法（交差検証）

データを学習用と検証用に分割し
検証用と学習用のデータを交代して、学習、評価する

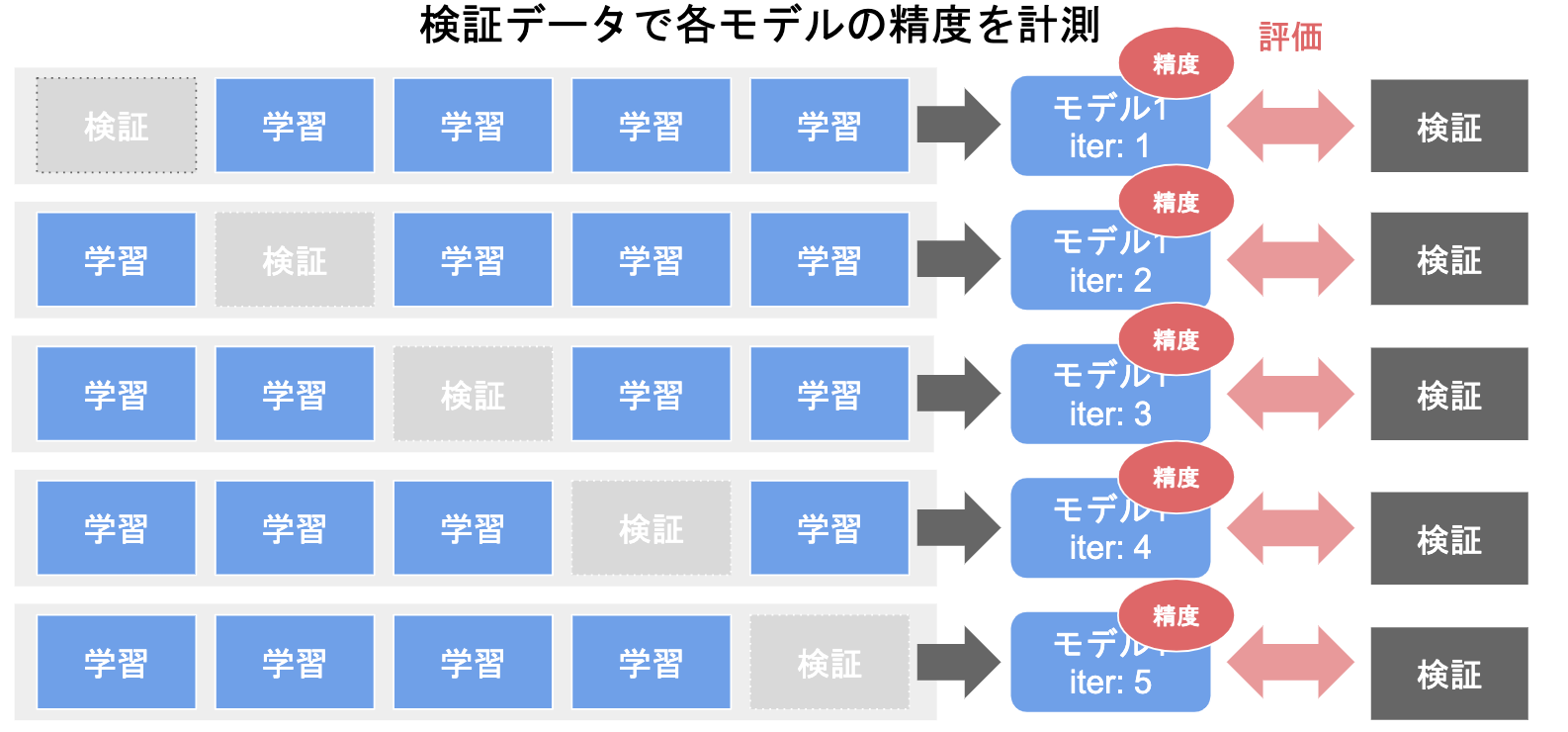
ホールドアウト法とクロスバリデーション法

ホールドアウトで検証したところ70％の精度、クロスバリデーションで65％の精度の場合、凡化精度の推定としてクロスバリデーション65％を採用する

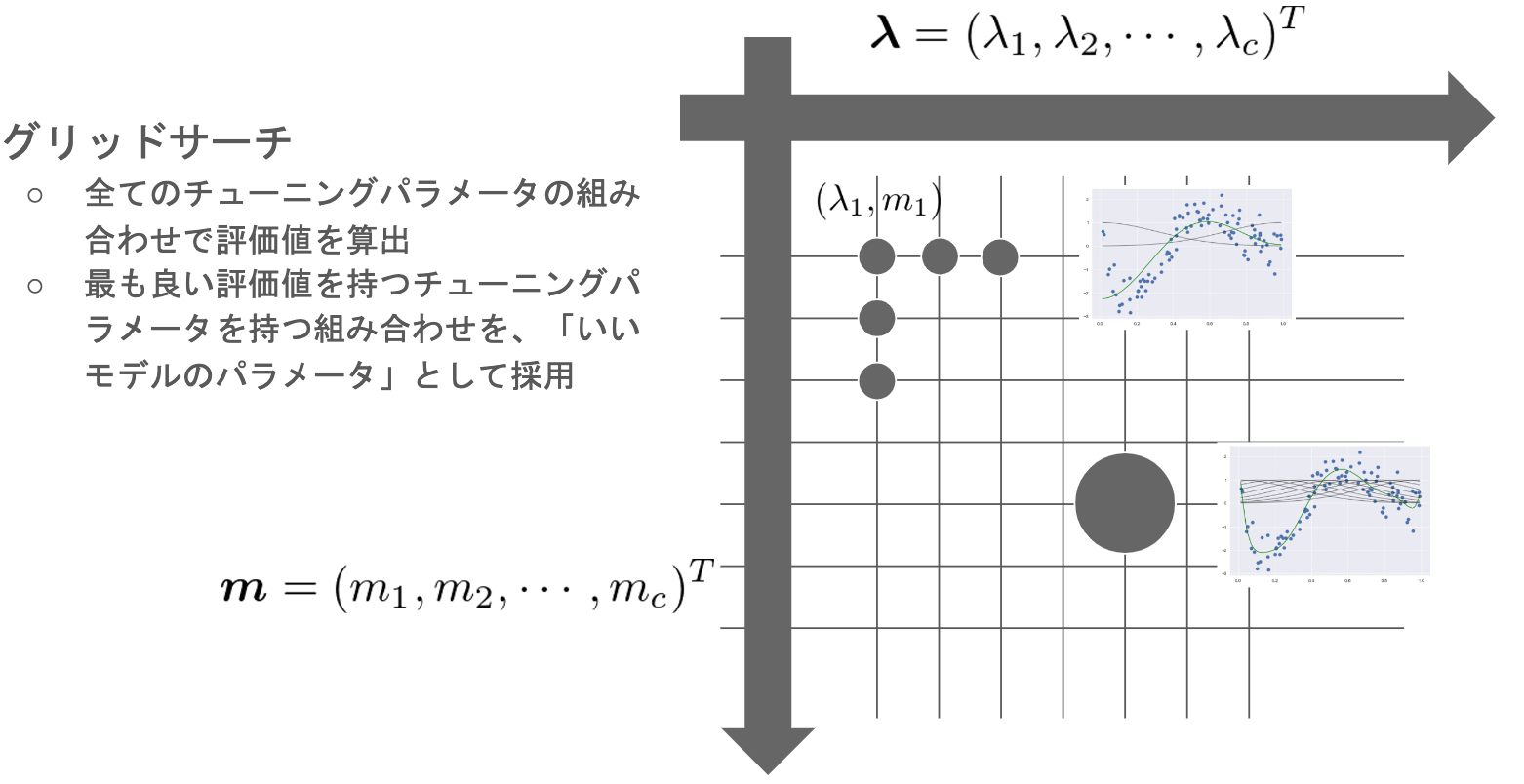
グリッドサーチ

適切なハイパーパラメータを選ぶ一つの方法

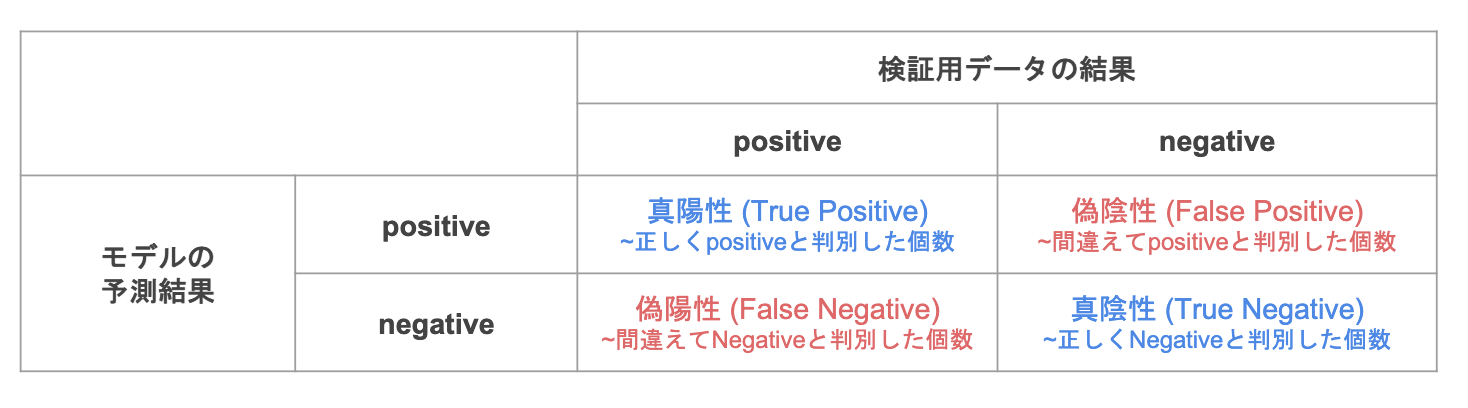
混同行列ーconfusion matrix

分類の評価方法

正解率の問題

正解した数/予測対象となった全データ数
分類したいクラスには偏りが多い場合、正解率の意味が薄くなる。
例：
メールのスパム分類：
スパム数が80件・普通のメール20件のデータの場合、
分類器は全てのメールをスパムとすると、正解率が80％になる、???

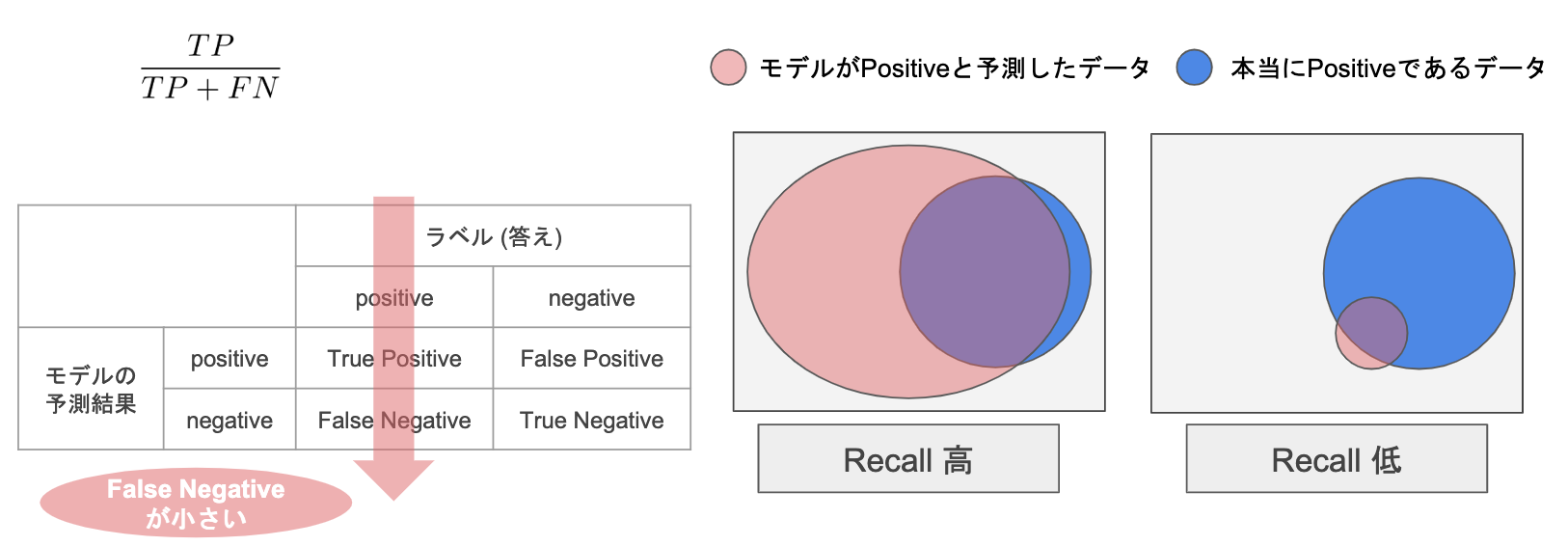
再現率ーRecall

「本当のPositiveなもの」の中からPositiveと予測した割合
誤りなものなにPositiveと予測したFalse Positive事情を考えない（多くてもいい）
例：病気の診断で陽性であるものを陰性（False Negative)と誤診としてしまうのを避けたい。
陰性であるものを陽性と誤診としてしまっても(False Positive)、再度、検査すれば、大丈夫からです。
※False Negativeを少なくしたい時

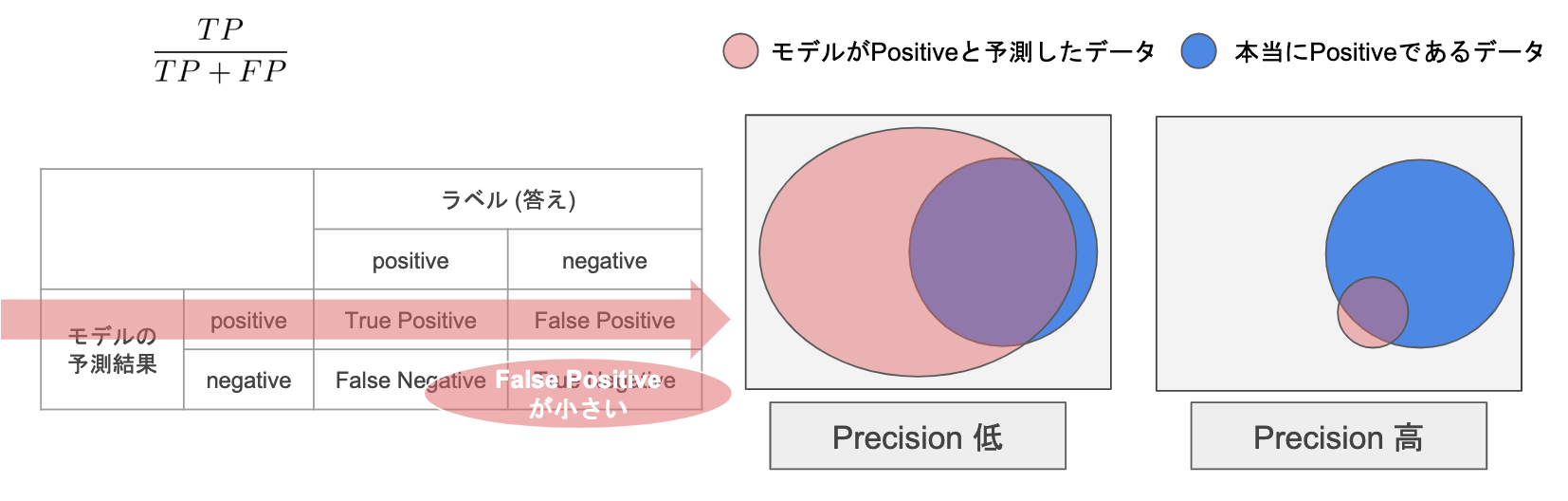
適合率ーPrecision

Positiveと予測したものの中から、本当のPositiveである割合
本当のものなのに、Negativeと予測したFalse Negative事情を考えない（多くてもいい）
例：大事なメールをスパム(False Positive)と誤検してしまうのを避けたい。
スパムであるものを普通のメールと誤検しても(False Negative)、自分でやればいい
※False Position を少なくしたい

F値

RecallとPrecisionはトレードオフの関係あり、どちらを小さくすると、片方の値が大きくなってします。
RecallとPrecisionの調和平均
RecallとPrecisionのバランスを示している。高ければ高いほど、RecallとPrecisionともに高くなる

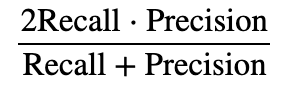
回帰問題について

ある入力値から出力値を予測する
例：賃貸の広さ、周辺状況を元に、家賃を予測する

直線で予測できる場合、線形回帰
曲線で予測できる場合、非線形回帰

線形回帰

単回帰

説明

参考

データ準備

n_sample = 100
var = .2

def linear_func(x):
    return 2 * x + 5

def add_noise(y_true, var):
    return y_true + np.random.normal(scale=var, size=y_true.shape)

def plt_result(xs_train, ys_true, ys_train):
    plt.scatter(xs_train, ys_train, facecolor="none", edgecolor="r", s=50,  label="training data")
    plt.plot(xs_train, ys_true, label="$2 x + 5$")
    plt.legend()

xs = np.linspace(0, 1, n_sample)
ys_true = linear_func(xs)
ys = add_noise(ys_true, var)

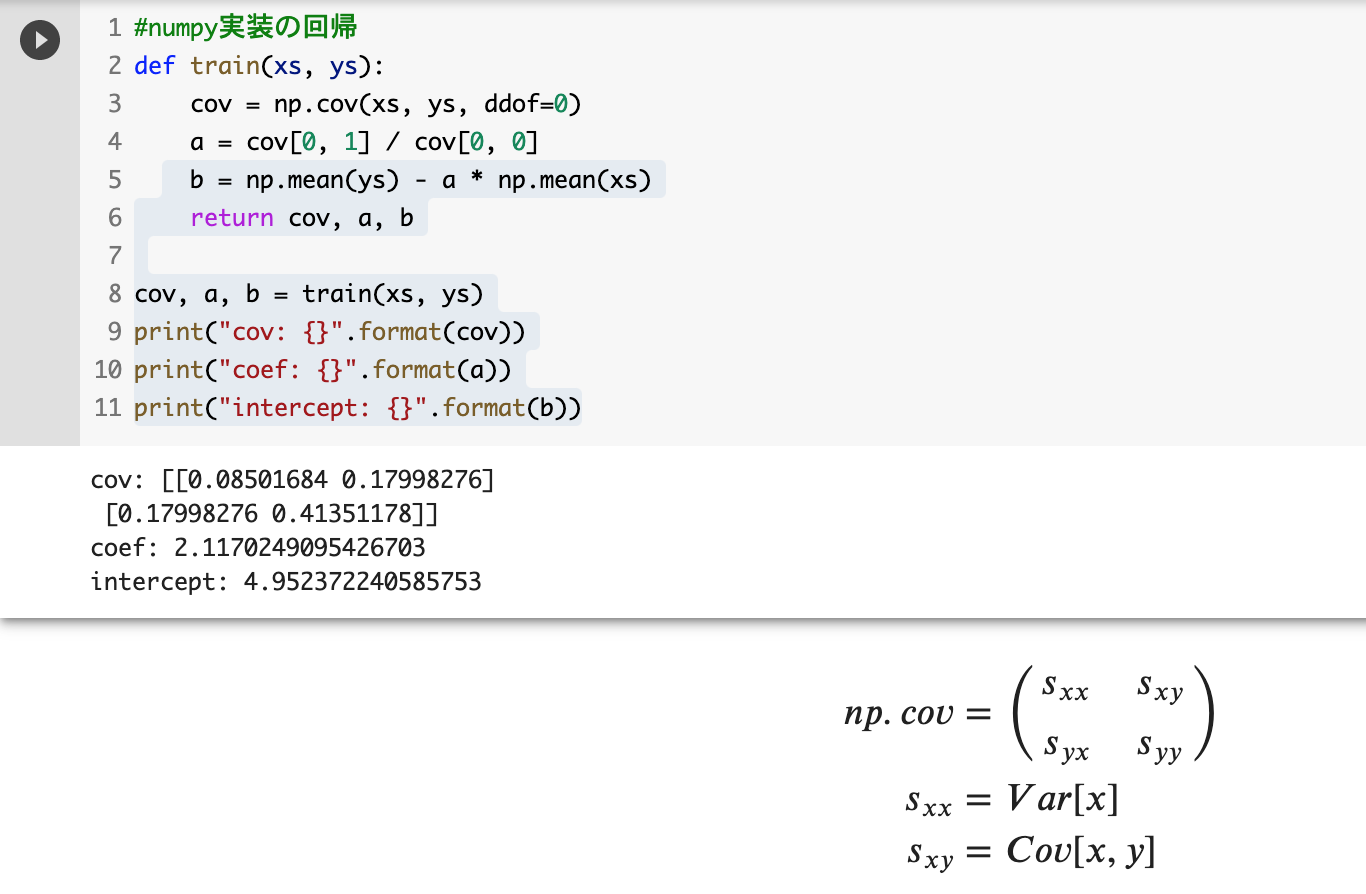
学習

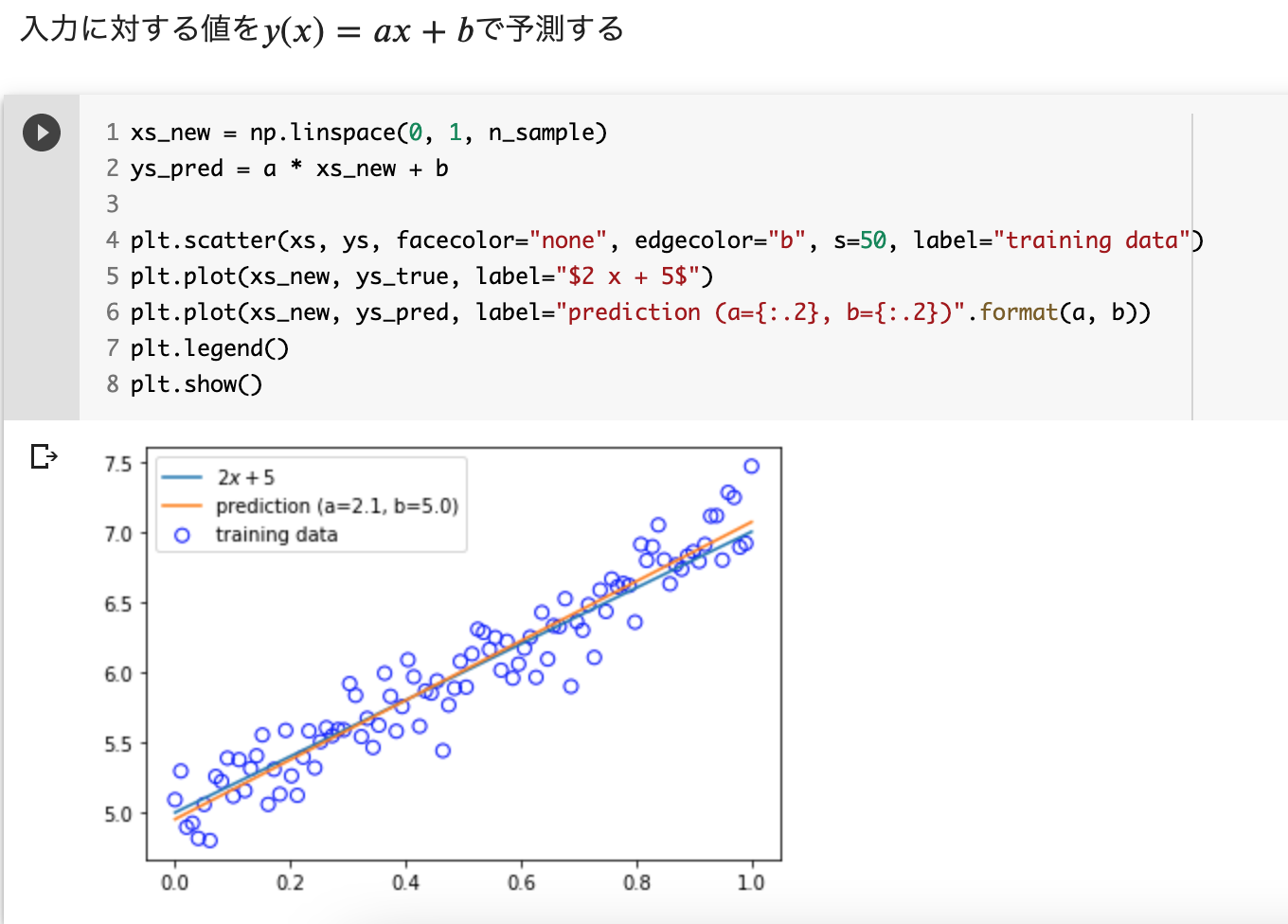
予測

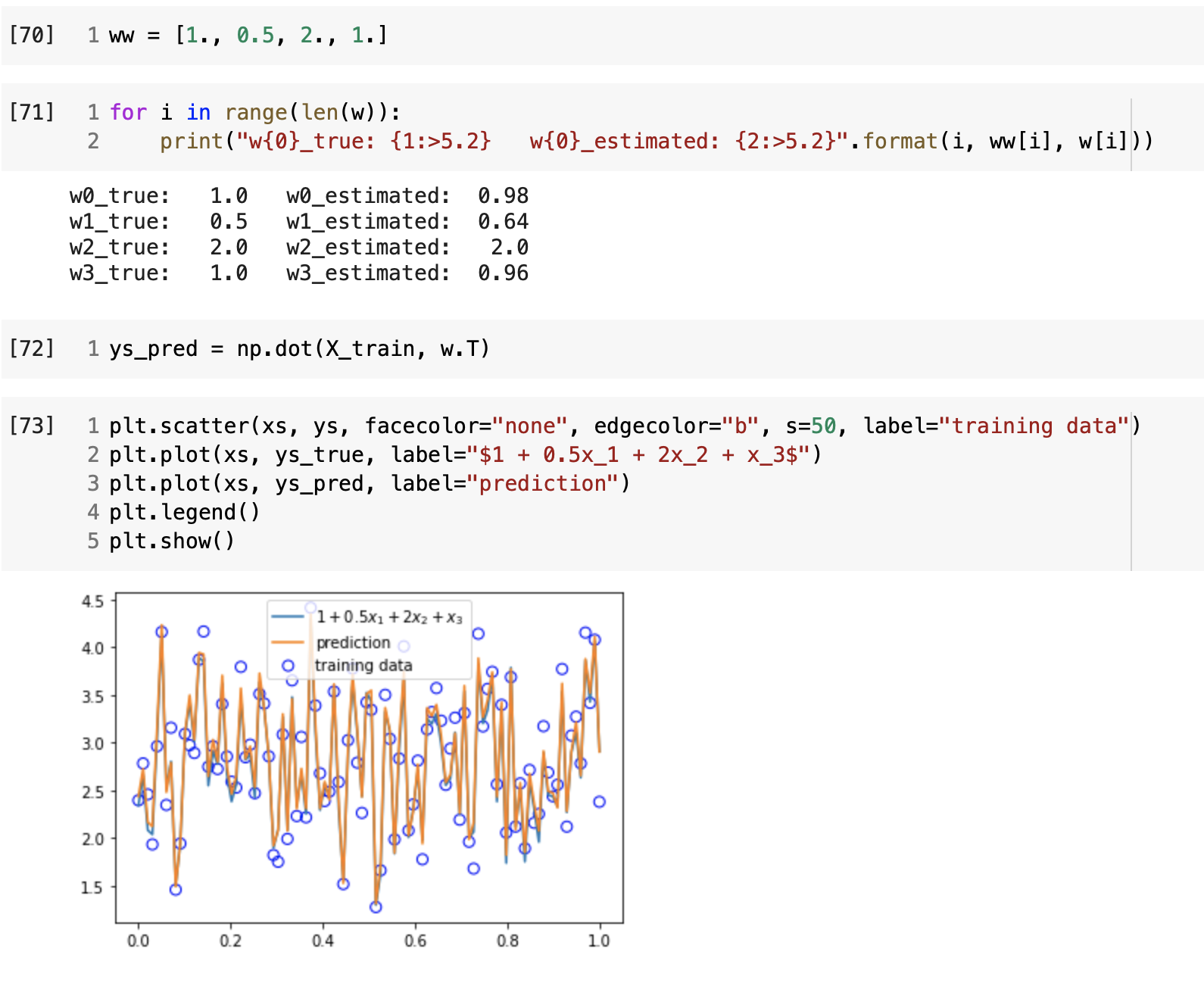
重回帰分析

データ準備

n_sample = 100
var = .2

def mul_linear_func(x):
    ww = [1., 0.5, 2., 1.]
    return ww[0] + ww[1] * x[:, 0] + ww[2] * x[:, 1] + ww[3] * x[:, 2]

def add_noise(y_true, var):
    return y_true + np.random.normal(scale=var, size=y_true.shape)

def plt_result(xs_train, ys_true, ys_train):
    plt.scatter(xs_train, ys_train, facecolor="none", edgecolor="b", s=50,  label="training data")
    plt.plot(xs_train, ys_true, label="$1 + 0.5x_1 + 2x_2 + x_3$")
    plt.legend()
x_dim = 3

X = np.random.random((n_sample, x_dim))
ys_true = mul_linear_func(X)
ys = add_noise(ys_true, var)
xs = np.linspace(0, 1, n_sample)
plt_result(xs, ys_true, ys)

学習

予測

考察

inputデータの次元が１に
Wの次元が２にしたら、単回帰になる

非線形回帰

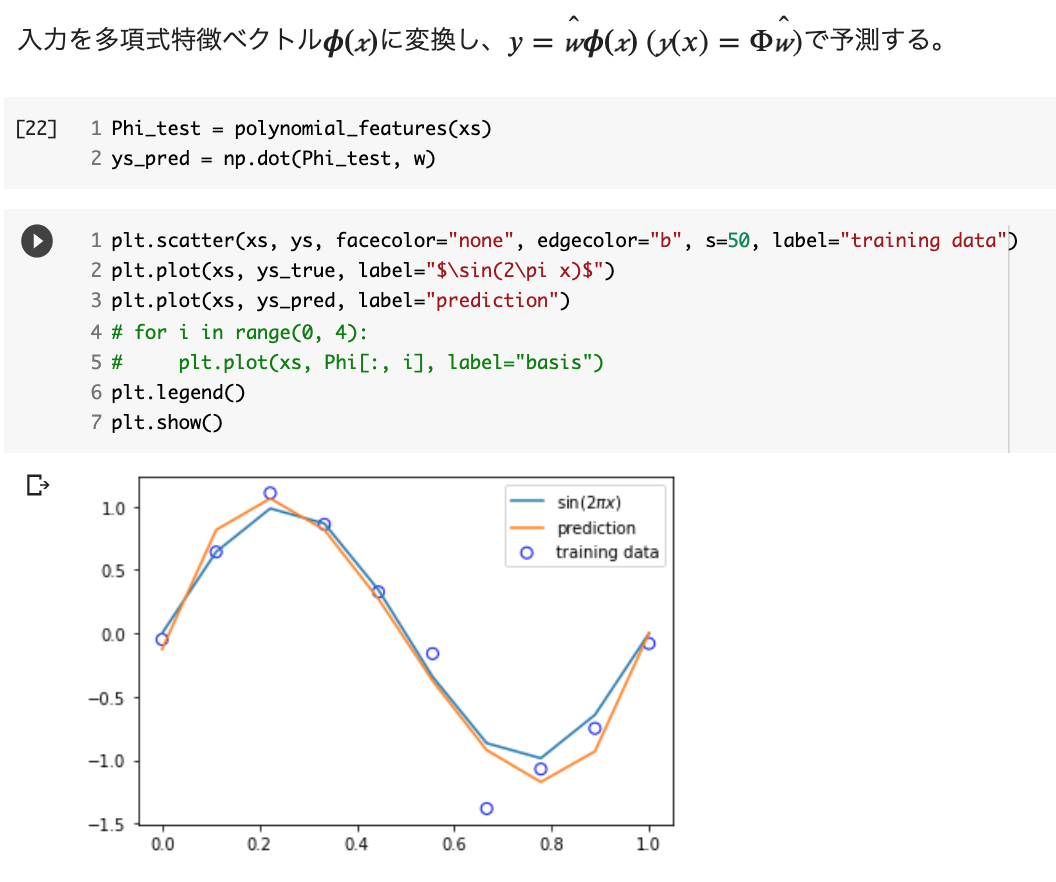
多項式回帰

データ準備

n_sample = 10
var = .25

def sin_func(x):
    return np.sin(2 * np.pi * x) 

def add_noise(y_true, var):
    return y_true + np.random.normal(scale=var, size=y_true.shape)

def plt_result(xs, ys_true, ys):
    plt.scatter(xs, ys,facecolor="none", edgecolor="b", s=50,  label="training data")
    plt.plot(xs, ys_true, label="$\sin(2\pi x)$")
    plt.legend()
#データの作成
xs = np.linspace(0, 1, n_sample)
ys_true = sin_func(xs)
ys = add_noise(ys_true, var)

print("xs: {}".format(xs.shape))
print("ys_true: {}".format(ys_true.shape))
print("ys: {}".format(ys.shape))

#結果の描画
plt_result(xs, ys_true, ys)

学習

予測

分類問題について

ある入力値に対して、クラスに分類する

ロジックティック回帰

Sigmoid（シグモイド）関数

\sigma(x) = \frac{1}{1 + \exp{(-ax)}}

微分

p(y=1 | \boldsymbol{x}; \boldsymbol{w}) = \sigma (\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x})

モデル

説明

最尤推定

尤度関数を最大化するようにパラメータを選ぶ推定

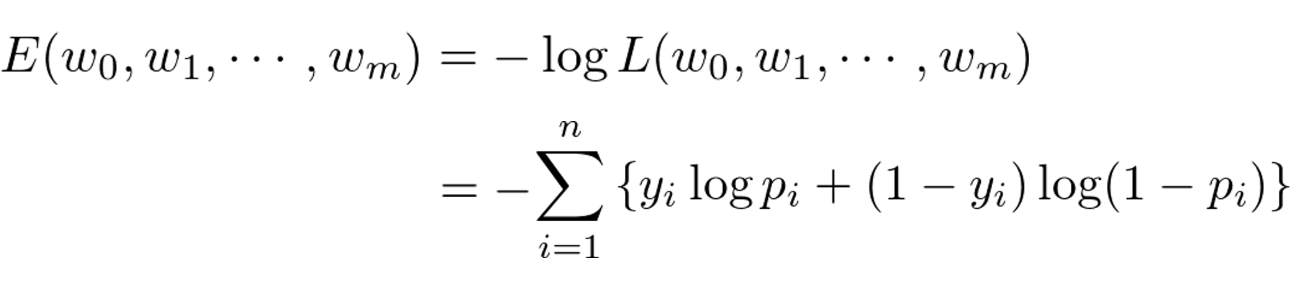
log対数を取る理由：
同時確率の積を和に変換可能
指数が積の演算に変換可能

対数尤度関数が最大値になる点と尤度関数が最大値になる点は同じ

−をかける理由：
「対数尤度関数の最小化」を「最小２乗法の最小化」と合わせる

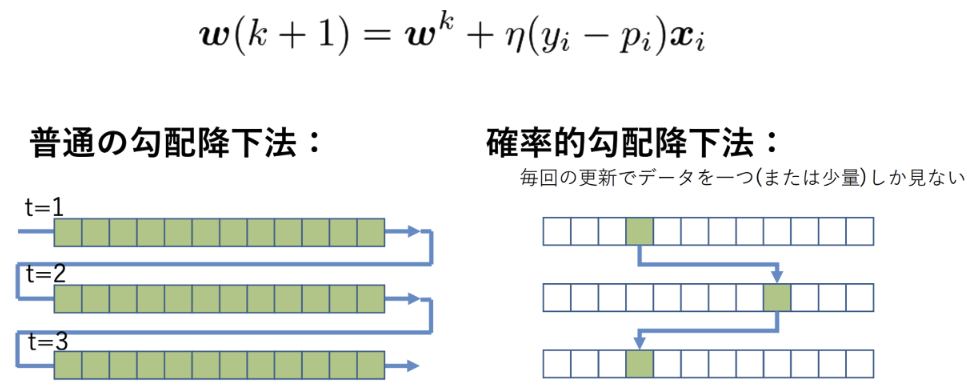
勾配降下法・Gradient Descent

反復学習によりパラメータを逐次的に更新する

なぜ必要？

線形回帰の場合：MSEのw微分が０になる \hat{w}を求められるが、\\
複雑な関数になると、直接に、\hat{w}を求めるのが難しいため

問題：
勾配降下では、パラメータを更新するため、全てのデータに対する和を求めないといけない。
膨大すぎるデータの場合、データをメモリに載せきれない問題が発生する。
この問題を解決するため、確率的な勾配降下を利用する

確率的勾配降下法・Stochastic Gradient Descent

データを一つずつランダムに選んで、パラメータを更新

データの準備

n_sample = 100
harf_n_sample = 50
var = .2

def gen_data(n_sample, harf_n_sample):
    x0 = np.random.normal(size=n_sample).reshape(-1, 2) - 1.
    x1 = np.random.normal(size=n_sample).reshape(-1, 2) + 1.
    x_train = np.concatenate([x0, x1])
    y_train = np.concatenate([np.zeros(harf_n_sample), np.ones(harf_n_sample)]).astype(np.int)
    return x_train, y_train

def plt_data(x_train, y_train):
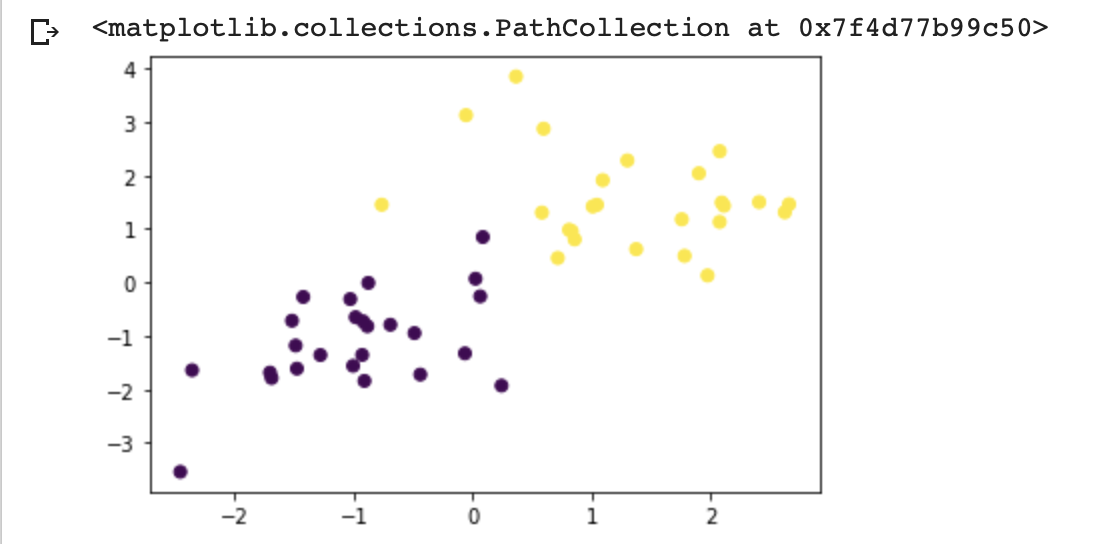
    plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, facecolor="none", edgecolor="b", s=50, label="training data")
    plt.legend()
#データ作成
x_train, y_train = gen_data(n_sample, harf_n_sample)
#データ表示
plt_data(x_train, y_train)
def add_one(x):
    return np.concatenate([np.ones(len(x))[:, None], x], axis=1)
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

勾配降下法・Gradient Descentの実装

def gd(X_train, max_iter, eta):
    w = np.zeros(X_train.shape[1])
    for _ in range(max_iter):
        w_prev = np.copy(w)
        sigma = sigmoid(np.dot(X_train, w))
        grad = np.dot(X_train.T, (sigma - y_train))
        w -= eta * grad
        if np.allclose(w, w_prev):
            return w
    return w
X_train = add_one(x_train)
max_iter=100
eta = 0.001
w_gd = gd(X_train, max_iter, eta)

確率的勾配降下法・Stochastic Gradient Descentの実装

def get_ramdom_batch(x, y, size=1):
  return_x = []
  return_y = []
  index_arr = [np.random.randint(0,y.shape[0]) for _ in range(0, size)]
  for index in index_arr:
    return_x.append(x[index])
    return_y.append(y[index])
  return np.array(return_x), np.array(return_y)
def sgd(X_train, max_iter, eta):
  w = np.zeros(X_train.shape[1])
  for _ in range(max_iter):
    w_prev = np.copy(w)
    x_batch, y_batch = get_ramdom_batch(X_train, y_train, 2)
    sigma = sigmoid(np.dot(x_batch, w))
    grad = np.dot(x_batch.T, (sigma - y_batch))
    w -= eta * grad
    if np.allclose(w, w_prev):
      return w
  return w
X_train = add_one(x_train)
max_iter=100
eta = 0.001
w_sgd = sgd(X_train, max_iter, eta)

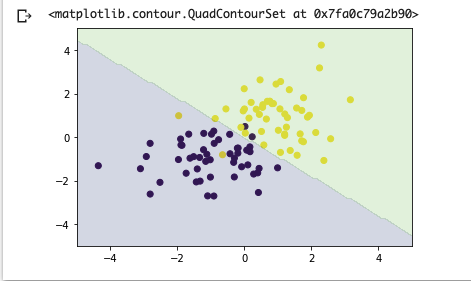
予測

xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

X_test = add_one(xx)
proba = sigmoid(np.dot(X_test, w_gd))
y_pred = (proba > 0.5).astype(np.int)
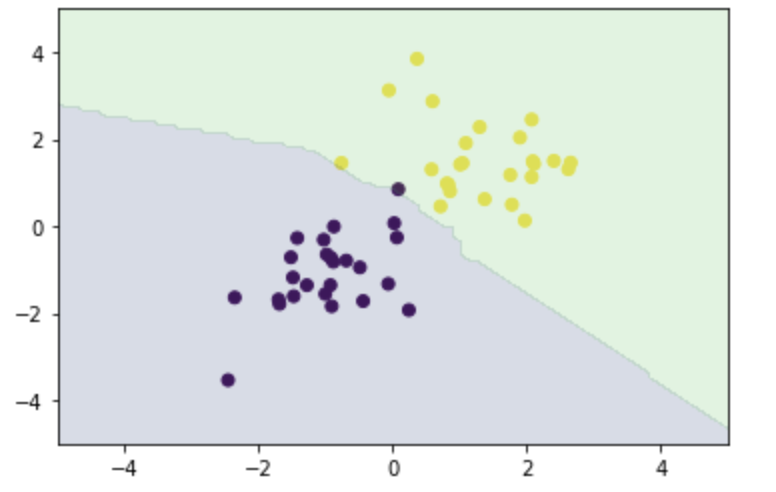
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))

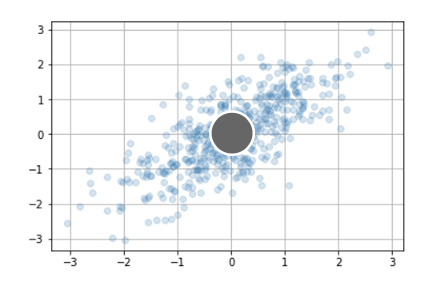
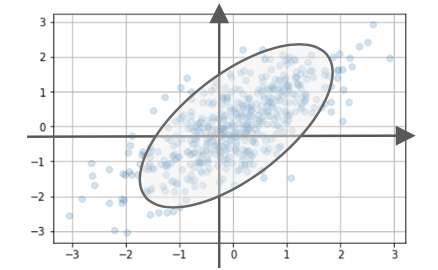
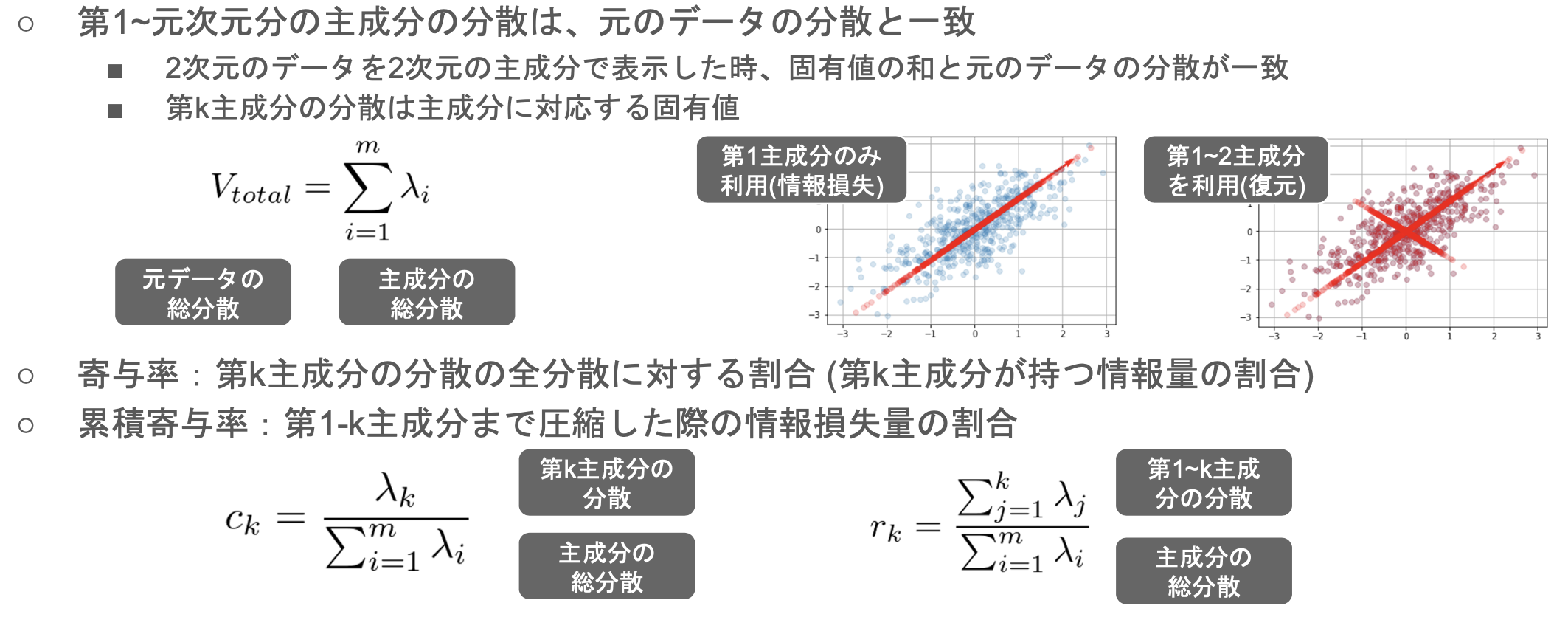
主成分分析

データ

平均-Mean

分散共分散行列

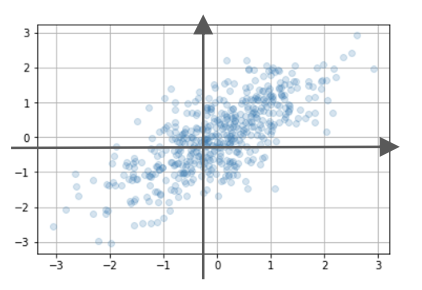
線形変化後のベクトル

aj:射影軸

線形変化後の分散

情報の量を分散の大きさを取り
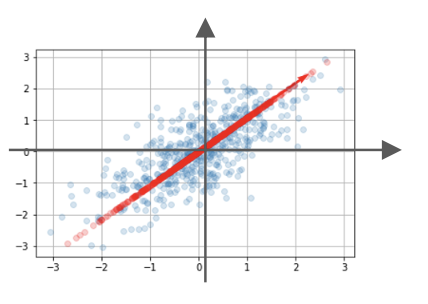
分散を最大となる射影軸ajを探索

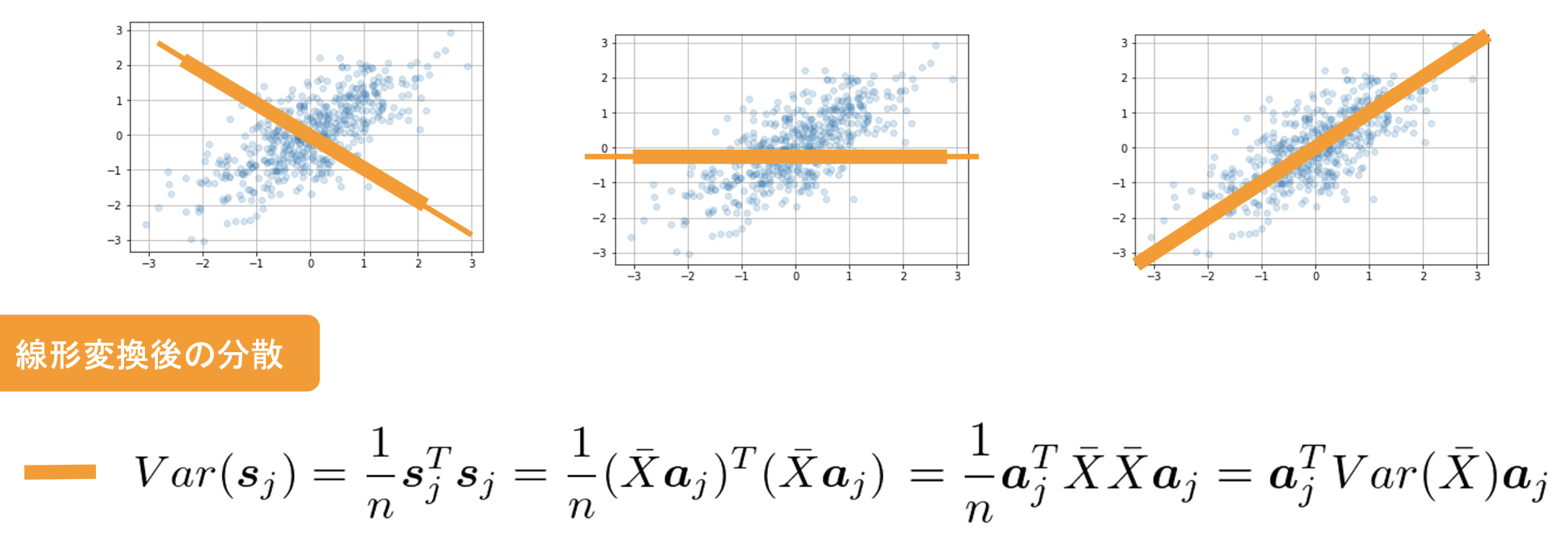
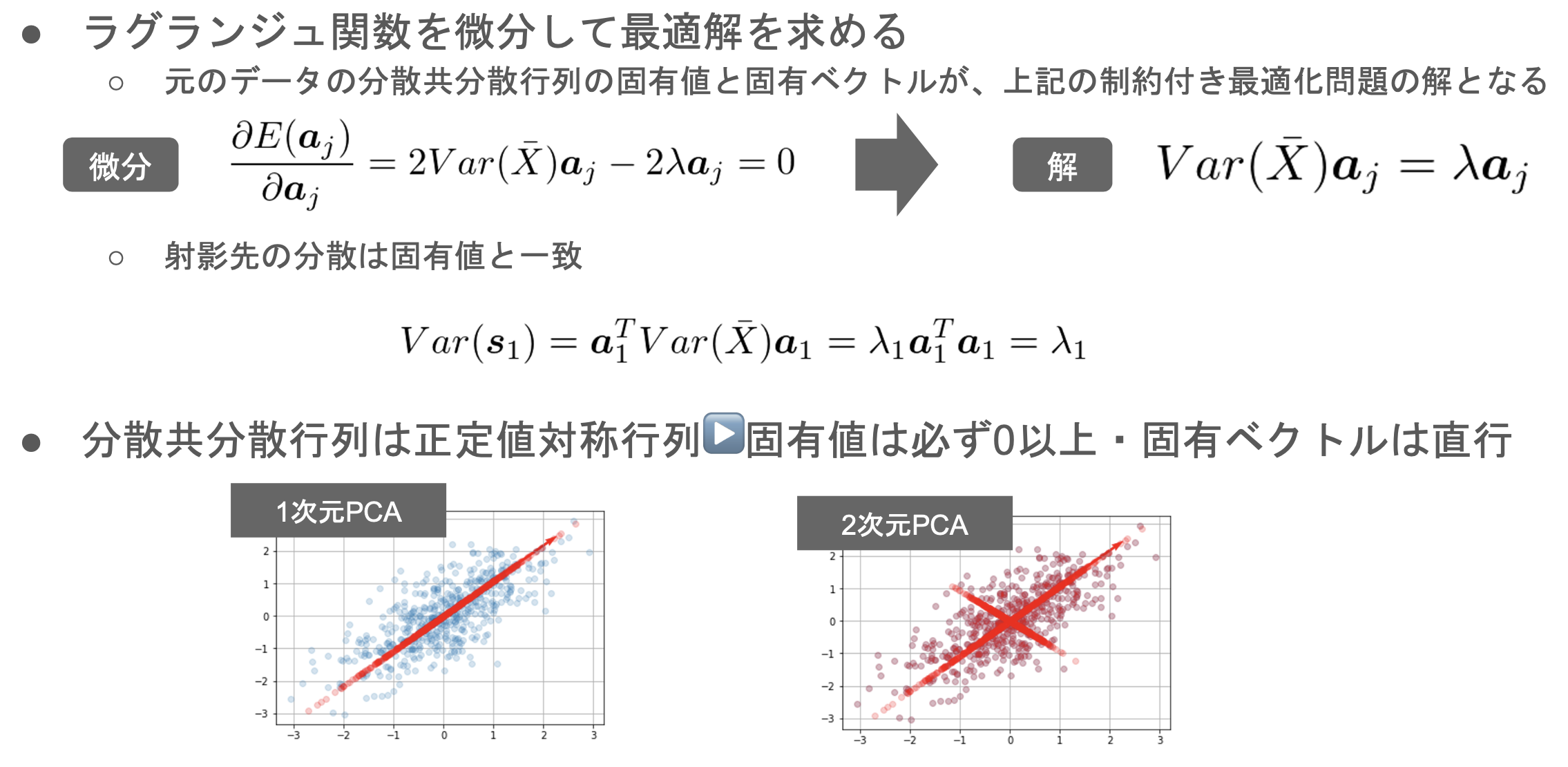
線形変化後の分散の最適化

主成分分析の求め方

寄与率

実装

33次元のデータで学習

# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)

# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))

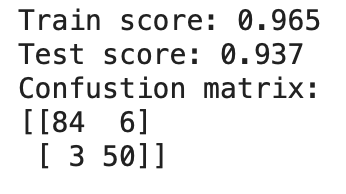
2次元へ圧縮したデータで学習

# 次元数2まで圧縮
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_pca, y_train)
X_test_pca = pca.transform(X_test_scaled)
# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_pca, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_pca, y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_pca))))

考察

検証スコアは97％→93％になったが、
学習がかかる時間が短縮され、計算コストが減ったメリットもある。
２次元へ圧縮するのが、あまり極端になるため、スコアが4％も下がった。
15次元（半分）へ圧縮したら、
検証スコアが高くなる期待できる。

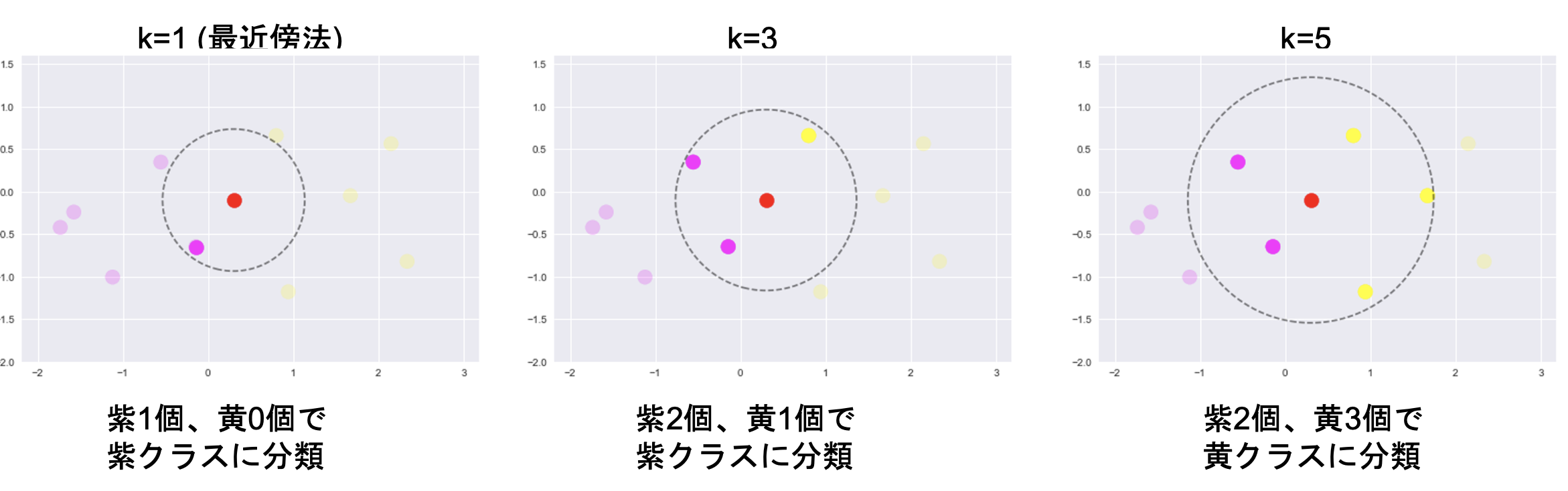
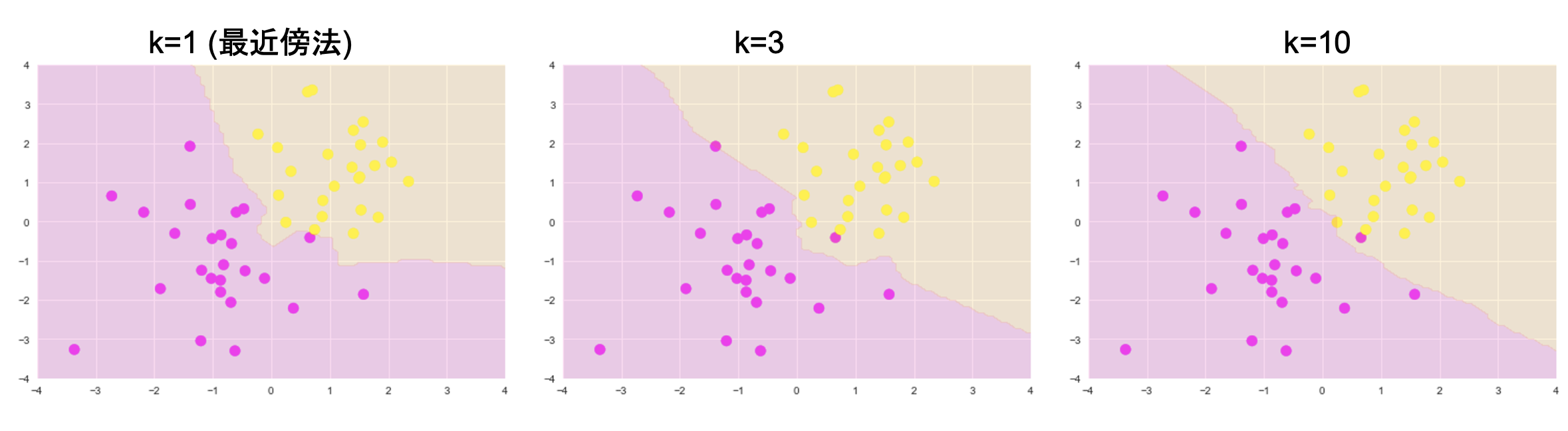
K近傍法・KNN

分類の機械学習手法
最近傍のデータからK個を取って、それらがもっとも多く所属するクラスに識別

Kが多くすると、決定境界が滑らかになる

実装

データの準備

def gen_data():
    x0 = np.random.normal(size=50).reshape(-1, 2) - 1
    x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
    x_train = np.concatenate([x0, x1])
    y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
    return x_train, y_train
X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)

予測

from scipy import stats
def distance(x1, x2):
    return np.sum((x1 - x2)**2, axis=1)

def knc_predict(n_neighbors, x_train, y_train, X_test):
    y_pred = np.empty(len(X_test), dtype=y_train.dtype)
    for i, x in enumerate(X_test):
        distances = distance(x, X_train)
        nearest_index = distances.argsort()[:n_neighbors]
        mode, _ = stats.mode(y_train[nearest_index])
        y_pred[i] = mode
    return y_pred

def plt_resut(x_train, y_train, y_pred):
    xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
    xx = np.array([xx0, xx1]).reshape(2, -1).T
    plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
    plt.contourf(xx0, xx1, y_pred.reshape(100, 100).astype(dtype=np.float), alpha=0.2, levels=np.linspace(0, 1, 3))
n_neighbors = 3

xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
X_test = np.array([xx0, xx1]).reshape(2, -1).T

y_pred = knc_predict(n_neighbors, X_train, ys_train, X_test)
plt_resut(X_train, ys_train, y_pred)

K平均法・K-Means

教師なし学習
クラスタリング手法
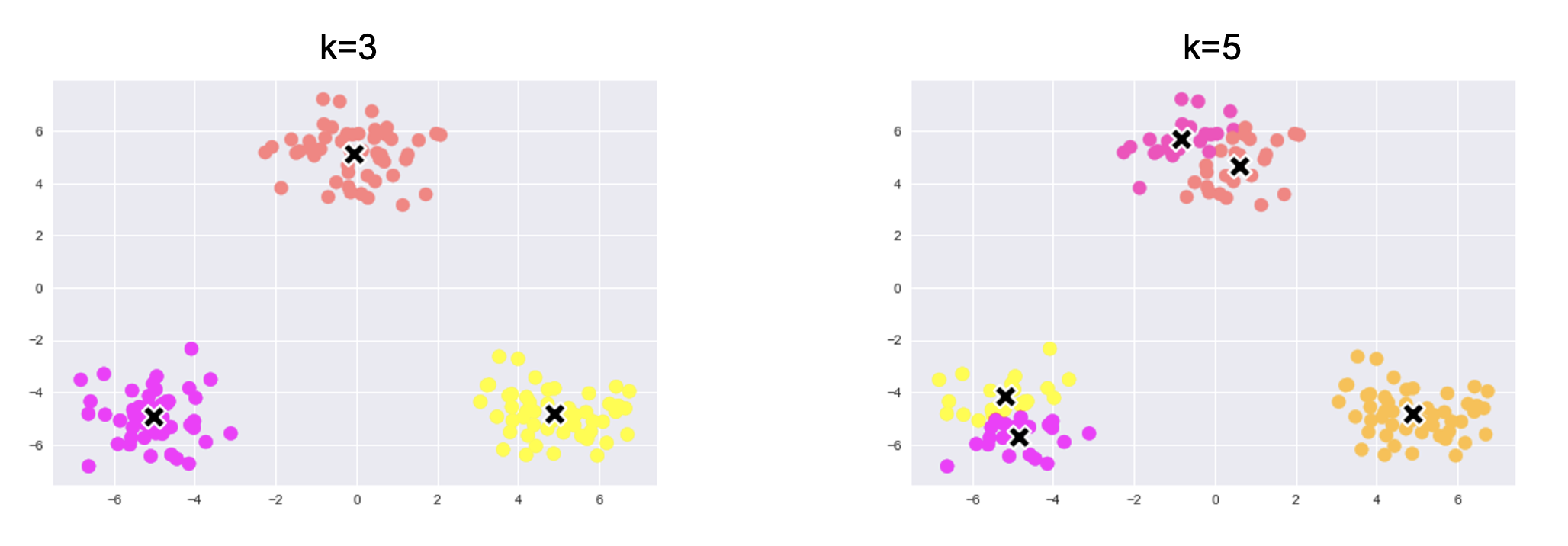
与えられたデータをK個のクラスタに分類

※クラスタリング：特徴の似ているもの同士をグループ化

アルゴリズム

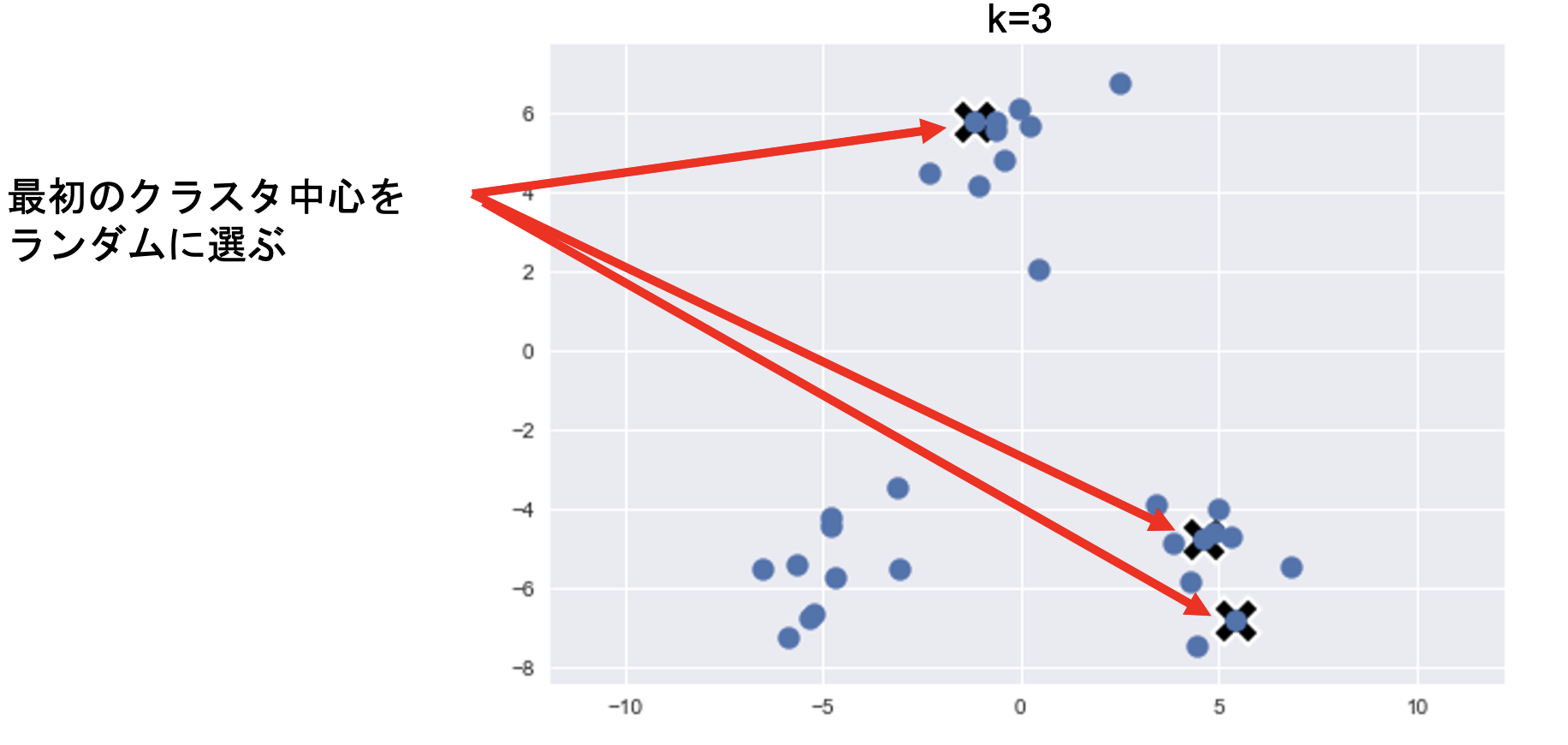
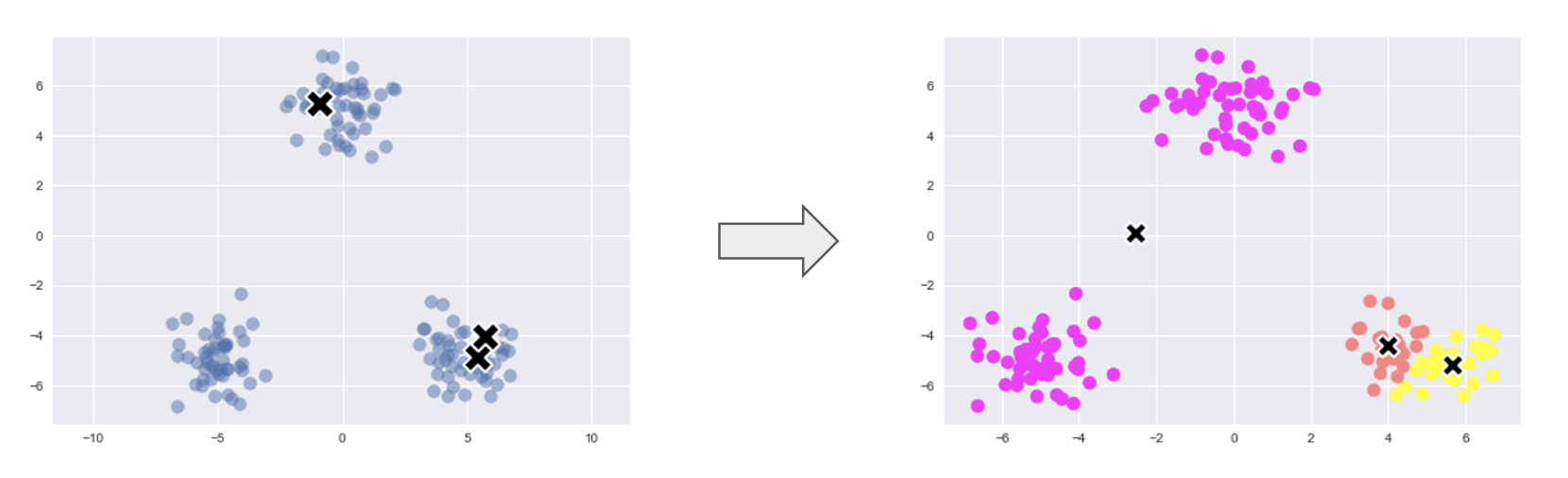
①各クラスタ中心の初期値の設定

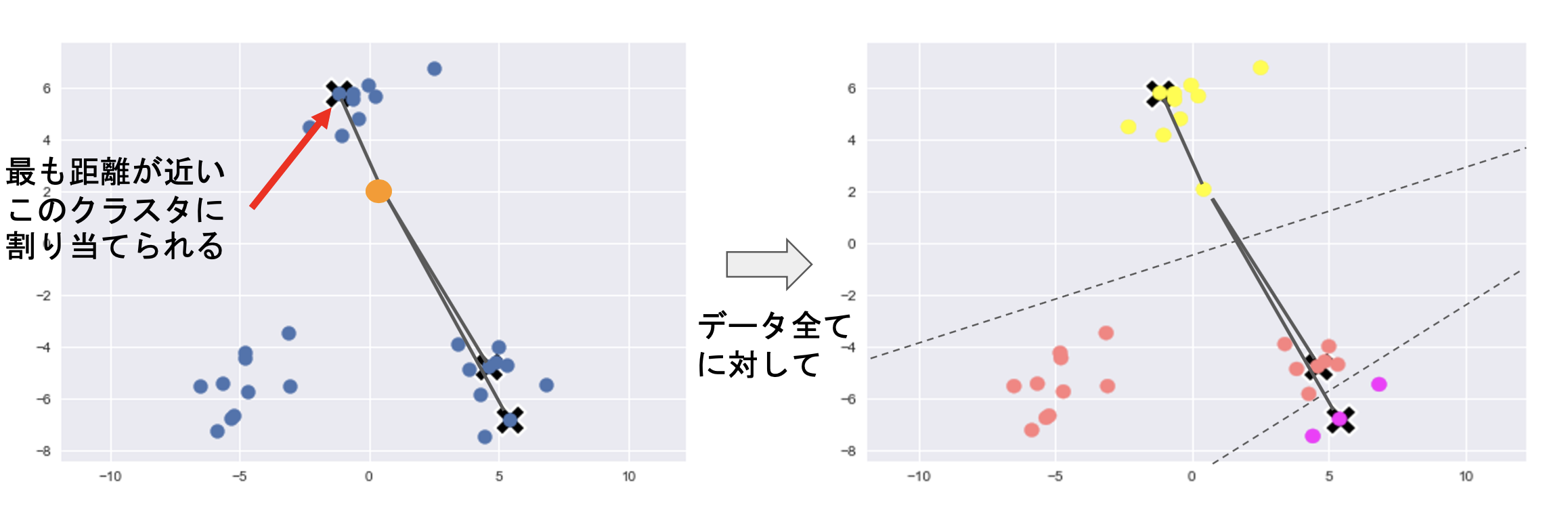
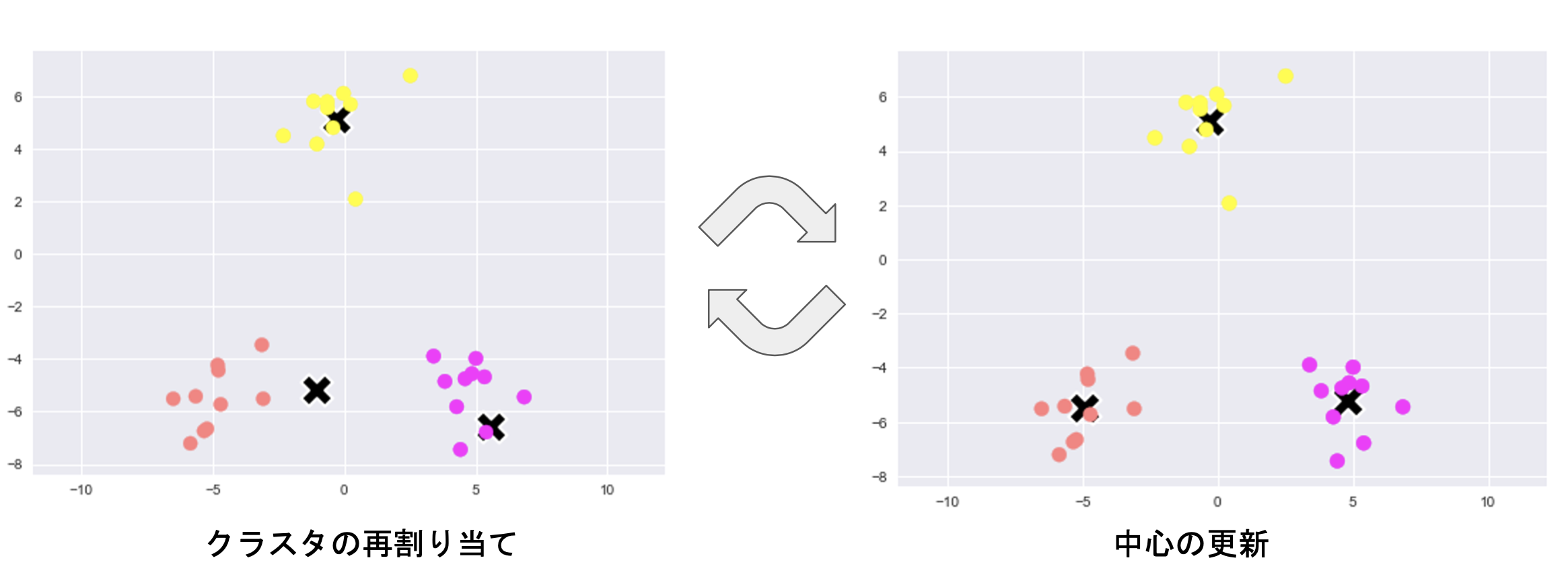
②各データ点に対して、各クラスタ中心との距離を計算し、最も、距離が近いクラスタを割り当てる

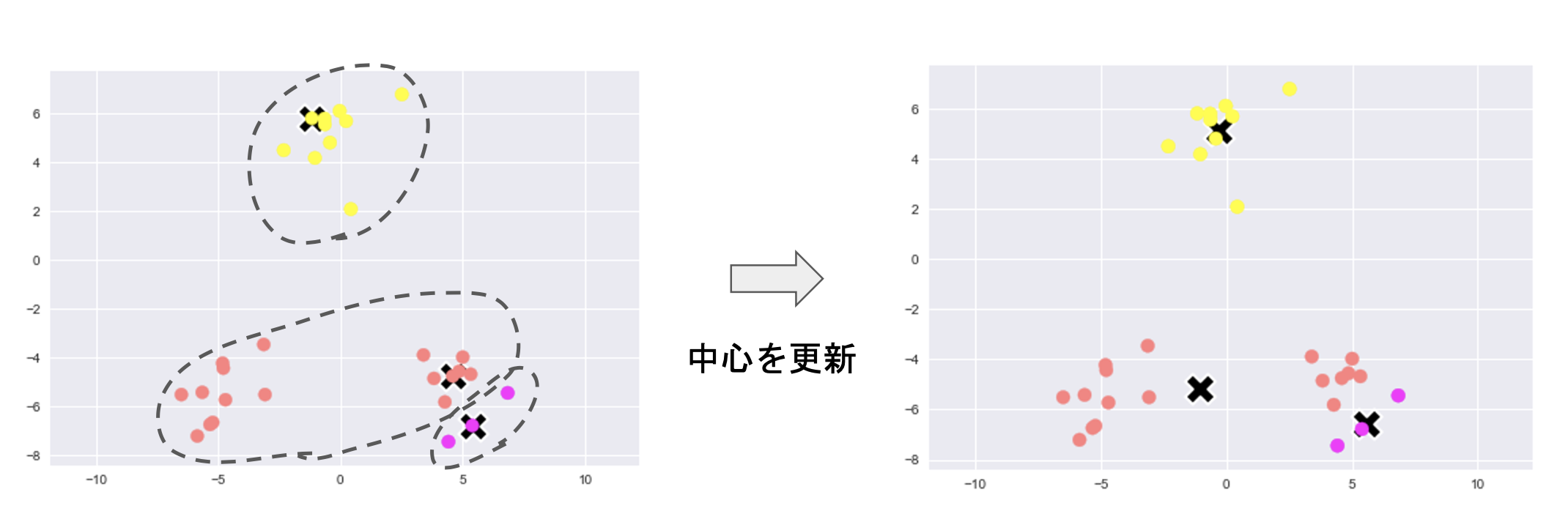
③各クラスタの平均ベクトル（中心）を計算

④クラスタの再割り当てると、中心の更新を繰り返し

考察

初期値が近くとクラスタリングがうまくいかない

Kの値を変えると、結果も変わる

実装

データ準備

def gen_data():
    x1 = np.random.normal(size=(100, 2)) + np.array([-5, -5])
    x2 = np.random.normal(size=(100, 2)) + np.array([5, -5])
    x3 = np.random.normal(size=(100, 2)) + np.array([0, 5])
    return np.vstack((x1, x2, x3))
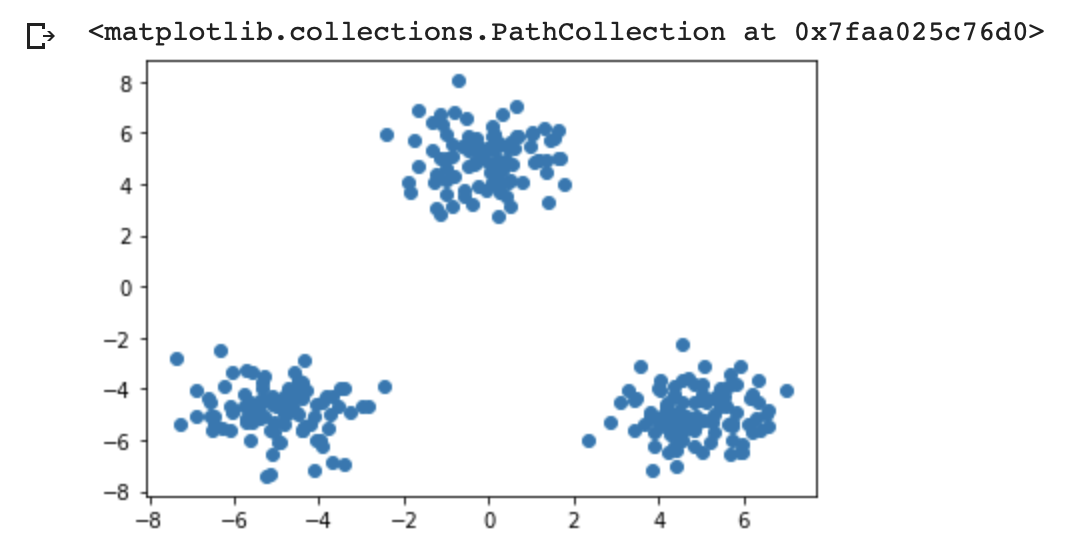
#データ作成
X_train = gen_data()
#データ描画
plt.scatter(X_train[:, 0], X_train[:, 1])

学習

def distance(x1, x2):
    return np.sum((x1 - x2)**2, axis=1)

n_clusters = 3
iter_max = 100

# 各クラスタ中心をランダムに初期化
centers = X_train[np.random.choice(len(X_train), n_clusters, replace=False)]

for _ in range(iter_max):
    prev_centers = np.copy(centers)
    D = np.zeros((len(X_train), n_clusters))
    # 各データ点に対して、各クラスタ中心との距離を計算
    for i, x in enumerate(X_train):
        D[i] = distance(x, centers)
    # 各データ点に、最も距離が近いクラスタを割り当
    cluster_index = np.argmin(D, axis=1)
    # 各クラスタの中心を計算
    for k in range(n_clusters):
        index_k = cluster_index == k
        centers[k] = np.mean(X_train[index_k], axis=0)
    # 収束判定
    if np.allclose(prev_centers, centers):
        break
y_pred = np.empty(len(X_train), dtype=int)
for i, x in enumerate(X_train):
    d = distance(x, centers)
    y_pred[i] = np.argmin(d)
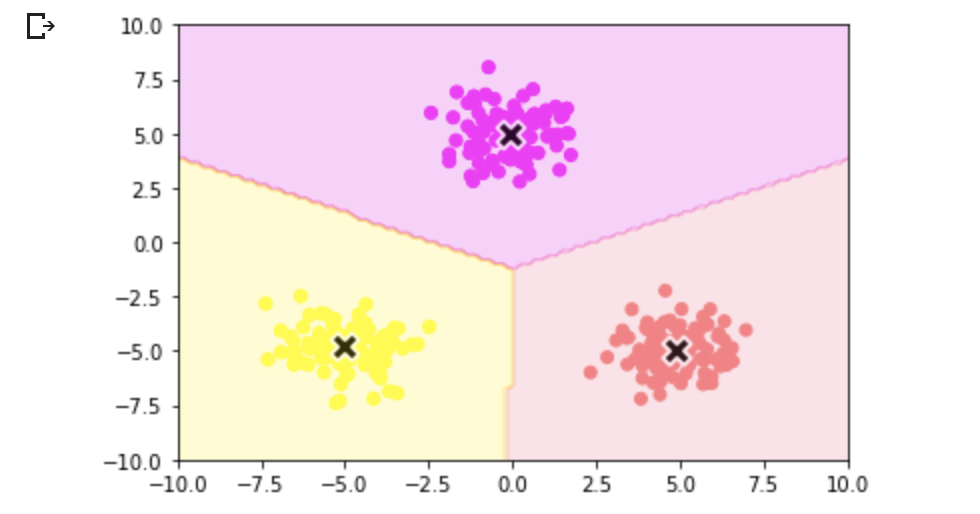
xx0, xx1 = np.meshgrid(np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

plt_result(X_train, centers, xx)

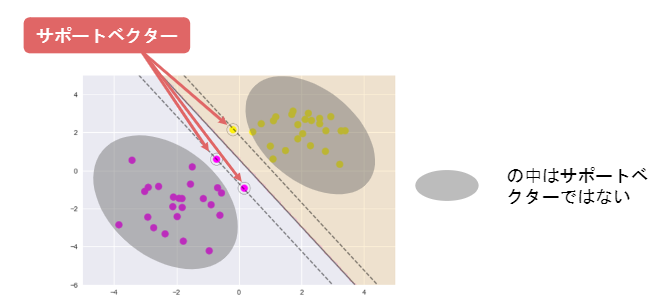
サポートベクターマシン（SVM）

2つクラス分類の手法

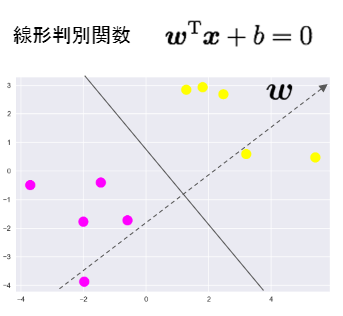
線形判別関数

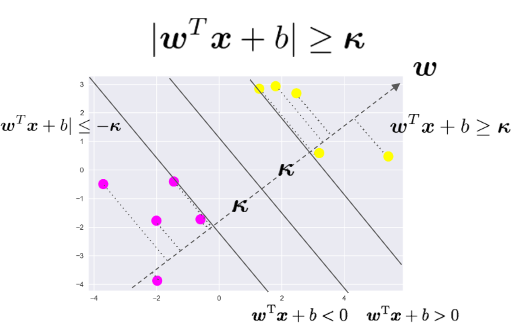
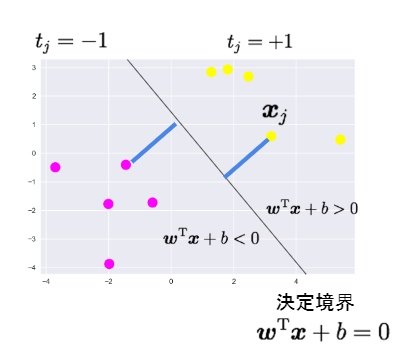
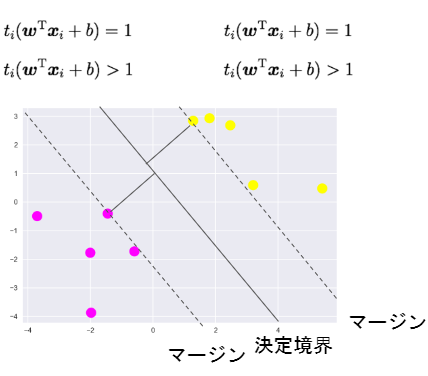
マージン

線形判別関数ともっとも近いデータ点との距離をマージンという
マージンを最大化するように線形判別関数を求める

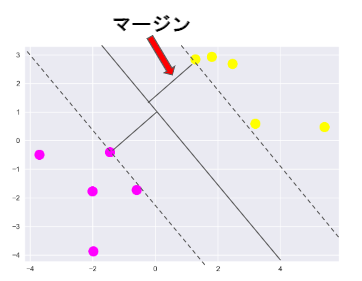
すべてデータ点をマージンと線形判別関数で表す

データ点から決定境界への距離

マージンとは決定境界ともっとも近い点との距離

目的関数

上記の式は以下のように同等
これはSVMの目的関数と制約条件
（※）式とする

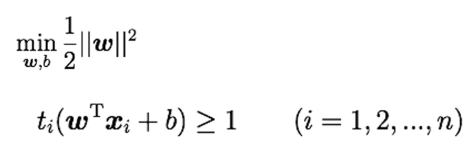
ラグランジュの未定乗数法

制約つき最適化問題を解く手法

KKT条件

制約つき最適化問題が満たす条件

SVMのラグランジュの未定乗数法・主問題

（※）式をラグランジュの未定乗数法を利用し

双対問題

w, bを消化

主問題と双対問題

主問題

w, b, a　に対して微分を求めて、各の微分式を0にイコールして、
連立法定式を利用して、最適なw, b, aを求める。

双対問題

aを求め方

def gen_data():
    x0 = np.random.normal(size=50).reshape(-1, 2) - 2.
    x1 = np.random.normal(size=50).reshape(-1, 2) + 2.
    X_train = np.concatenate([x0, x1])
    ys_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
    return X_train, ys_train
X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
t = np.where(ys_train == 1.0, 1.0, -1.0)

n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)

eta1 = 0.01
eta2 = 0.001
n_iter = 500

H = np.outer(t, t) * K

a = np.ones(n_samples)
for _ in range(n_iter):
    grad = 1 - H.dot(a)
    a += eta1 * grad
    a -= eta2 * a.dot(t) * t
    a = np.where(a > 0, a, 0)

ｗを求め方

bを求め方

計算上以下のように利用されている。

予測

index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]

term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
    for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
        y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)

# 訓練データを可視化
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                    s=100, facecolors='none', edgecolors='k')
# 領域を可視化
#plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                     levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])


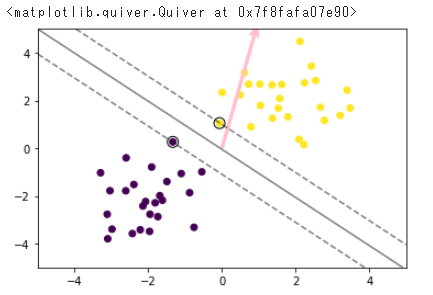
# マージンと決定境界を可視化
plt.quiver(0, 0, 0.1, 0.35, width=0.01, scale=1, color='pink')

サポートベクターのイメージ

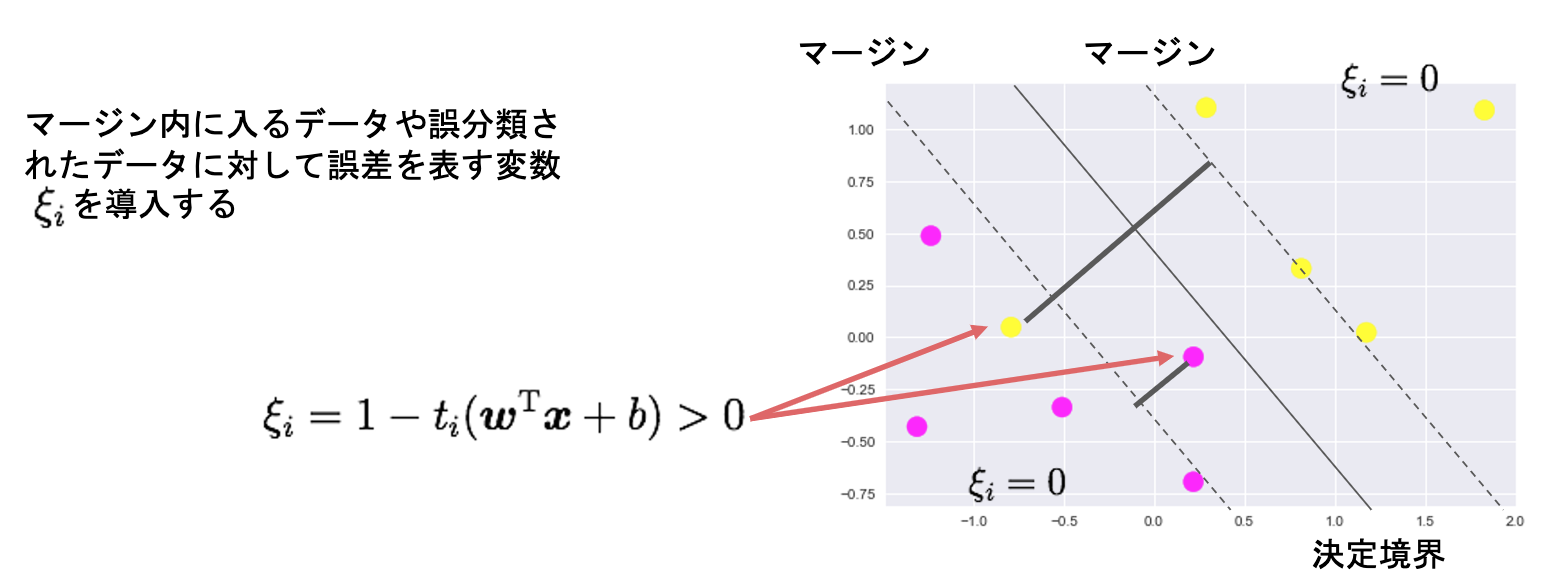
ソフトマージンSVM

線形分類できない場合（同じクラスに属するデータは同じ側に在るが、たまに、反対クラスの側にあるデータ（孤立のデータ））
以下の写真には、黄色の一点がピンク色の点の側に在る

誤差を許容し、誤差に対して、ペナルティを与える

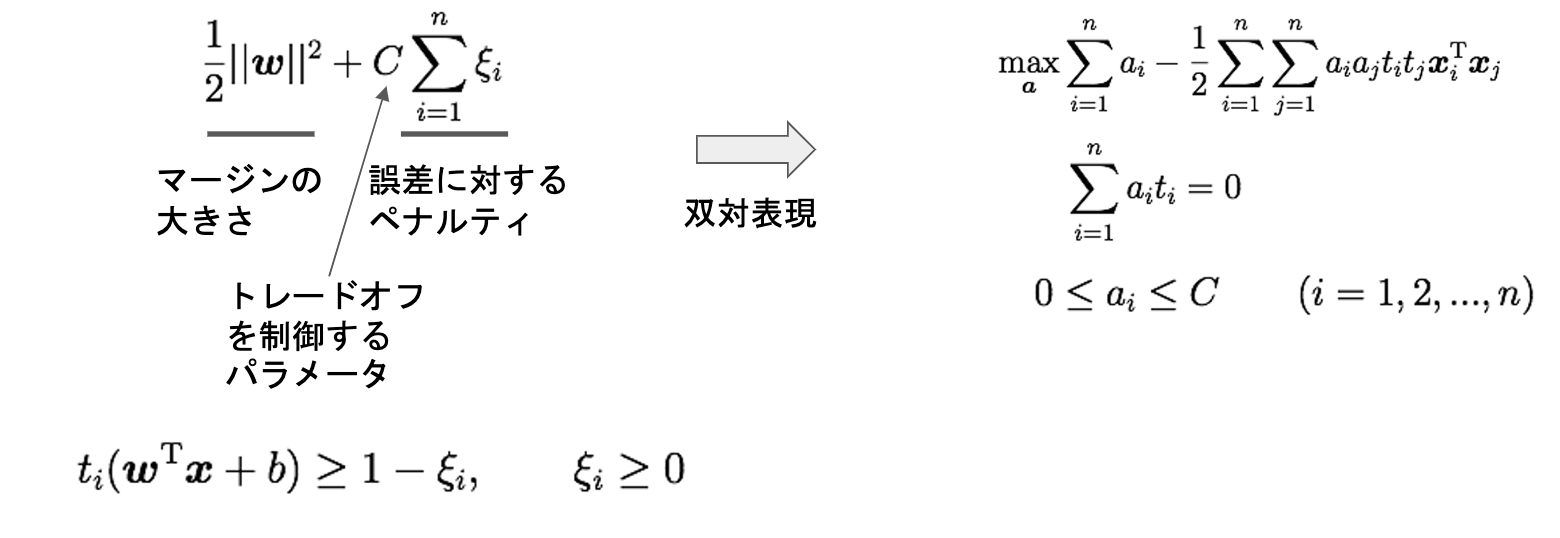
目的変数と制約条件

双対変数への展開

性質

基本、普通のSVMにパラメータCが追加された
パラメータCの大小で決定境界が変わる

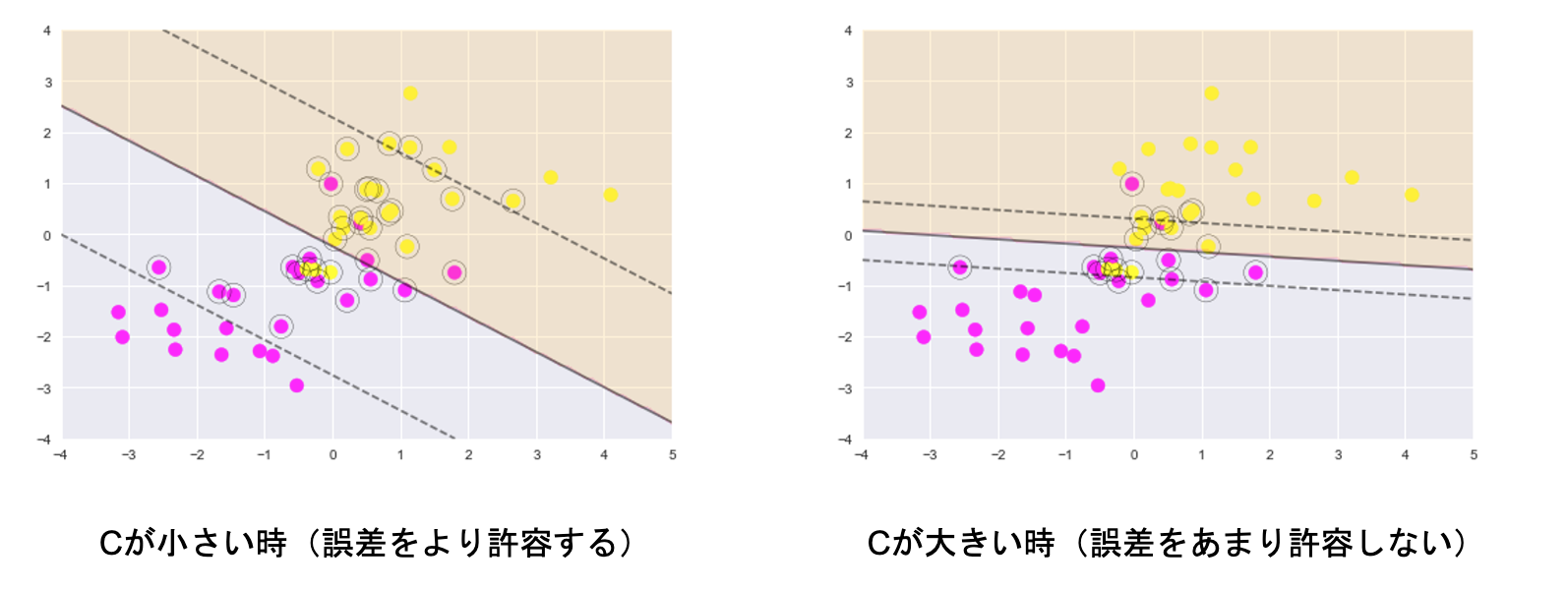
実装

データの準備

x0 = np.random.normal(size=50).reshape(-1, 2) - 1.
x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
x_train = np.concatenate([x0, x1])
y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)

学習

X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)

n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)

C = 1
eta1 = 0.01
eta2 = 0.001
n_iter = 1000

H = np.outer(t, t) * K

a = np.ones(n_samples)
for _ in range(n_iter):
    grad = 1 - H.dot(a)
    a += eta1 * grad
    a -= eta2 * a.dot(t) * t
    a = np.clip(a, 0, C)

予測

index = a > 1e-8
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]

term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

xx0, xx1 = np.meshgrid(np.linspace(-4, 4, 100), np.linspace(-4, 4, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
    for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
        y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)

# 訓練データを可視化
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                    s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                     levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])

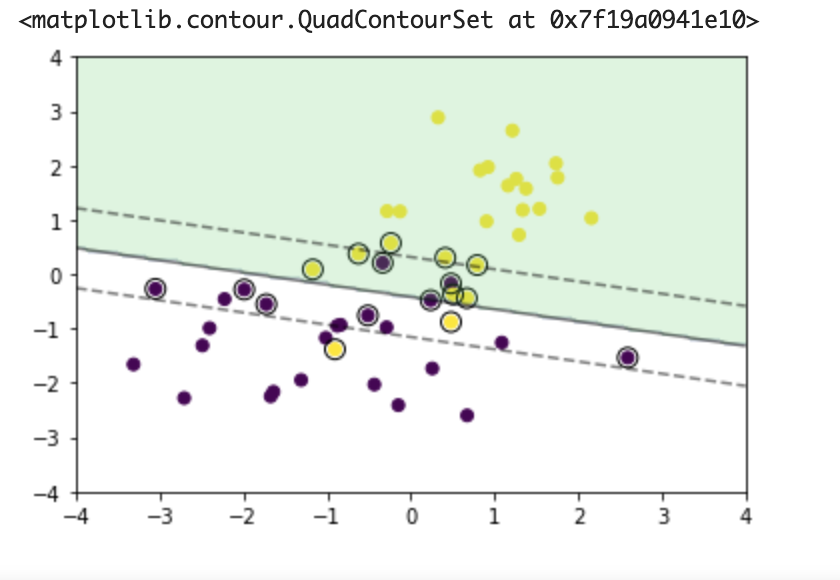
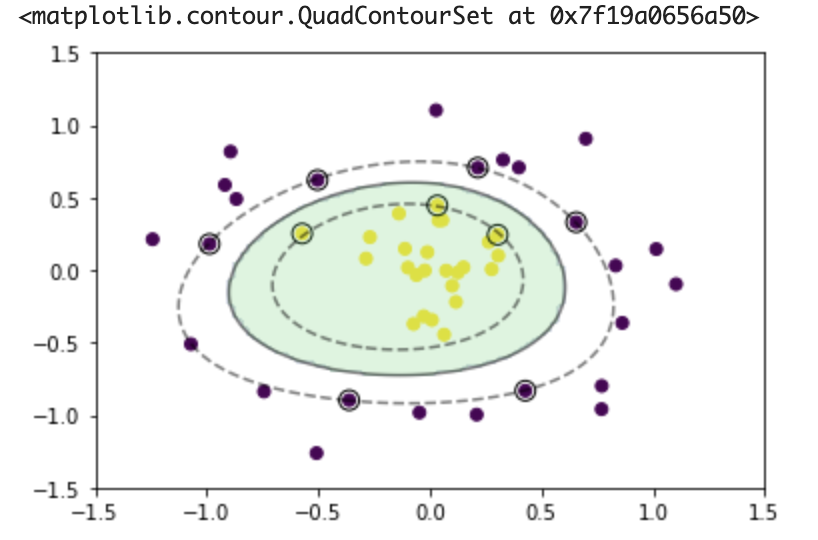
カーネルSVM

線形でないデータの場合
特徴空間に写像し、その空間に、線形のデータになる

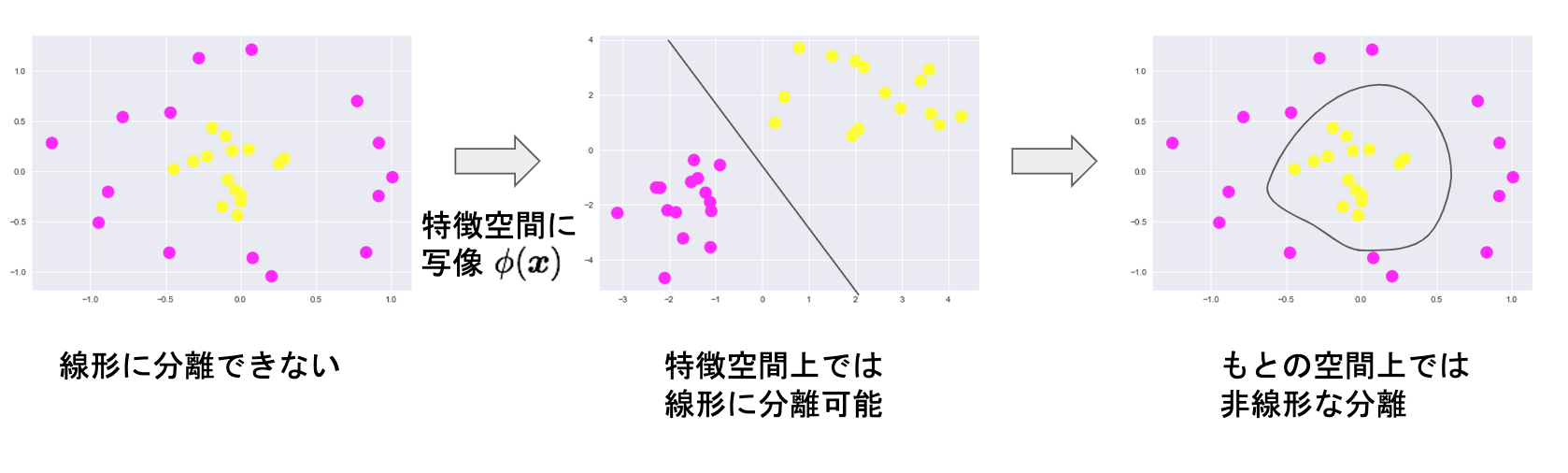
目的関数

カーネルトリック

高次元ベクトルの内積をスカラー関数で表現できる
特徴空間が高次元でも計算コストを抑えられる

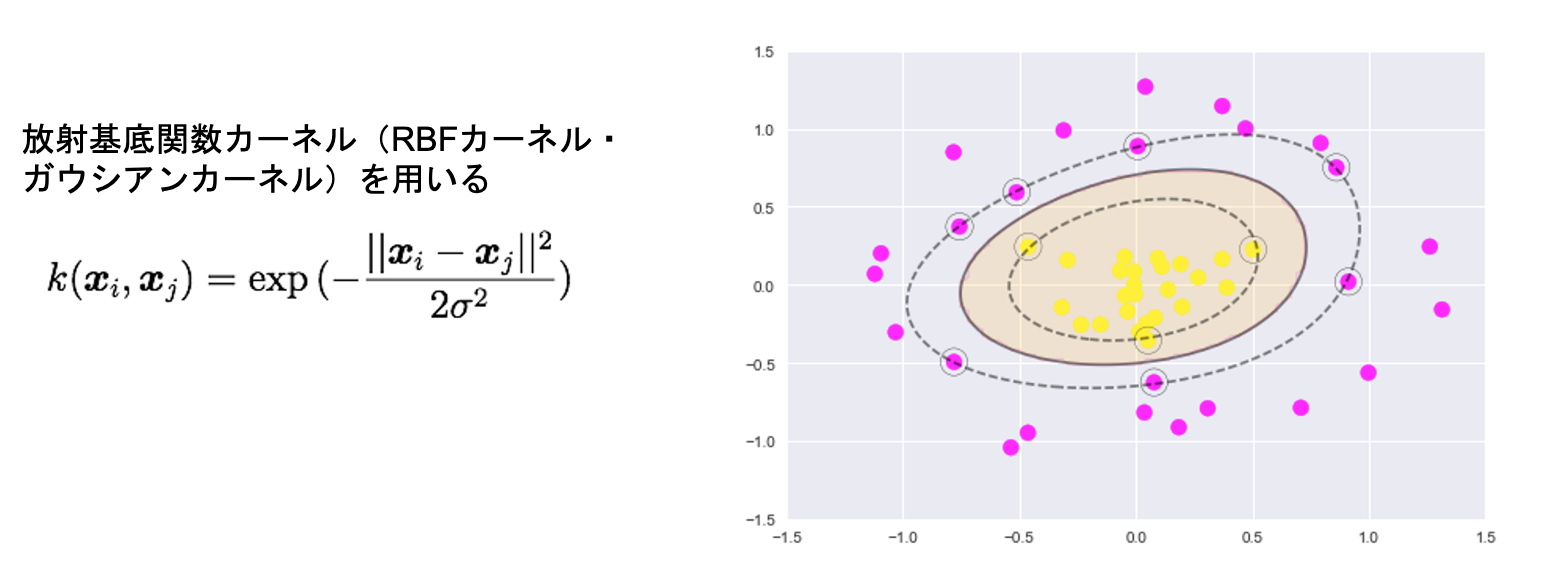
カーネル関数

実装

データ準備

factor = .2
n_samples = 50
linspace = np.linspace(0, 2 * np.pi, n_samples // 2 + 1)[:-1]
outer_circ_x = np.cos(linspace)
outer_circ_y = np.sin(linspace)
inner_circ_x = outer_circ_x * factor
inner_circ_y = outer_circ_y * factor

X = np.vstack((np.append(outer_circ_x, inner_circ_x),
               np.append(outer_circ_y, inner_circ_y))).T
y = np.hstack([np.zeros(n_samples // 2, dtype=np.intp),
               np.ones(n_samples // 2, dtype=np.intp)])
X += np.random.normal(scale=0.15, size=X.shape)
x_train = X
y_train = y

plt.scatter(x_train[:,0], x_train[:,1], c=y_train)

学習

def rbf(u, v):
        sigma = 0.8
        return np.exp(-0.5 * ((u - v)**2).sum() / sigma**2)

X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)

n_samples = len(X_train)
# RBFカーネル
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
    for j in range(n_samples):
        K[i, j] = rbf(X_train[i], X_train[j])

eta1 = 0.01
eta2 = 0.001
n_iter = 5000

H = np.outer(t, t) * K

a = np.ones(n_samples)
for _ in range(n_iter):
    grad = 1 - H.dot(a)
    a += eta1 * grad
    a -= eta2 * a.dot(t) * t
    a = np.where(a > 0, a, 0)

予測

index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]

term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

xx0, xx1 = np.meshgrid(np.linspace(-1.5, 1.5, 100), np.linspace(-1.5, 1.5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T

X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
    for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
        y_project[i] += a * sv_t * rbf(X_test[i], sv)
y_pred = np.sign(y_project)

# 訓練データを可視化
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                    s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                     levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])