はじめに
有志での勉強会の教材としてRによる統計的学習入門を使用してます。
その7章の「線形を超えて」では、一般化加法モデル(Generalized Additive Models, GAM)という手法が出てきます。
非線形関数を使用しながら説明性も担保していることから、推論にも使いやすいという手法ということで、これを自分なりの理解の範囲で簡単にまとめたいと思います。
GAMの概要
線形モデルの説明性をなるべく維持しながら、非線形モデルの複雑なモデル作成を両立させるための方法という理解です。
まず、p次元の線形重回帰モデルは次の式で表せます。
y_t = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + ・・・ + \beta_px_{ip} + \epsilon_i
これを拡張して、各線形成分なめらかな非線形関数である$f_j(x_{ji})$に置き換えることで、表現力を上げます。
y_t = \beta_0 + f_1(x_{i1}) + f_2(x_{i2}) + ・・・ + f_p(x_{ip}) + \epsilon_i
入力データの1変数ごとに非線形関数を生成してその和を取っているので、加法モデルと呼ぶとのことです。
GAMの利点と欠点
利点は次の通り。
- 通常の線形回帰では捉えられない非線形の関係を自動的にモデル化できる。
- モデルが加法的なので、1次元ごとに応答変数への効果を見ることができる。したがって推論向き。
欠点は次の通り。
- 加法に限定されているので、変数が多いと交互作用をとられることが難しい。ただし、線形モデルと同様に$ X_i * X_j $を追加することで、交互作用項をGAMに加えることは可能。
- 外挿の予測について、線形モデルより脆弱と思われる(データの無い領域については、どんな手法でもどうしようもない側面はありますが。)
Rだとgamパッケージで、PythonだとpyGAMライブラリで使えるようなので、使ってみます。
RでGAMを使う
gamパッケージで利用可能なので、使ってみます。
ここでは、Rによる統計的学習入門の7.9演習問題の(7)の自分なりの答えを例にやってみます。
まず、ここではWageデータを使います。これはこの教科書実習用のライブラリISLRに格納されているデータで、3000人の男性の賃金(Wage)とそれに関係ありそうな変数(year(西暦)、age(年齢)、婚姻状況(maritl)、人種(race)、健康状態(health)、保険の有無(health_ins)など)が集まったものです。
詳しくはR Package Documentation:Wage: Mid-Atlantic Wage DataやWageのhelpを見てください。
また、yearとageはこの教科書の本文で既に触れられているので、今回は考慮外としGAMモデル生成時には格納するものとします。すみません。
ここでは、Wageを目的変数として、他の変数が説明変数となりうるかをGAMで見てみます。
まず、Wageデータを統計量や簡単な可視化で確認してみます。
# Wageと他の説明変数との関係をGAMで確認する。
## データのロード
library(ISLR)
attach(Wage)
## helpを確認。
## Mid-Atlantic Wage Data(https://rdrr.io/cran/ISLR/man/Wage.html)と同一の情報が見れます。
?Wage
## 各説明変数の基本統計量の確認
summary(maritl)
summary(race)
summary(jobclass)
summary(health)
summary(health_ins)
summary(region) #helpにmid-atlantic onlyと記載あり
## ボックスプロットで分布を確認
par(mfrow = c(2,3))
plot(maritl, wage, main="maritl & wage", xlab="martil", ylab="wage")
plot(race, wage, main="race & wage", xlab="race", ylab="wage")
plot(jobclass, wage, main="jobclass & wage", xlab="jobclass", ylab="wage")
plot(health, wage, main="health & wage", xlab="health", ylab="wage")
plot(health_ins, wage, main="health_ins & wage", xlab="health_ins", ylab="wage")
plot(region, wage, main="region & wage", xlab="region", ylab="wage") #helpにmid-atlantic onlyと記載あり
ここまでを実行すると、サマリの結果と次のボックスプロットを確認することができます。
1. Never Married 2. Married 3. Widowed 4. Divorced 5. Separated
648 2074 19 204 55
1. White 2. Black 3. Asian 4. Other
2480 293 190 37
1. Industrial 2. Information
1544 1456
1. <=Good 2. >=Very Good
858 2142
1. Yes 2. No
2083 917
1. New England 2. Middle Atlantic 3. East North Central 4. West North Central 5. South Atlantic
0 0 0 0 3000
6. East South Central 7. West South Central 8. Mountain 9. Pacific
0 0 0 0
これで、説明変数ごとの各カテゴリの分布状況を数値とボックスプロットの両方で確認できました。
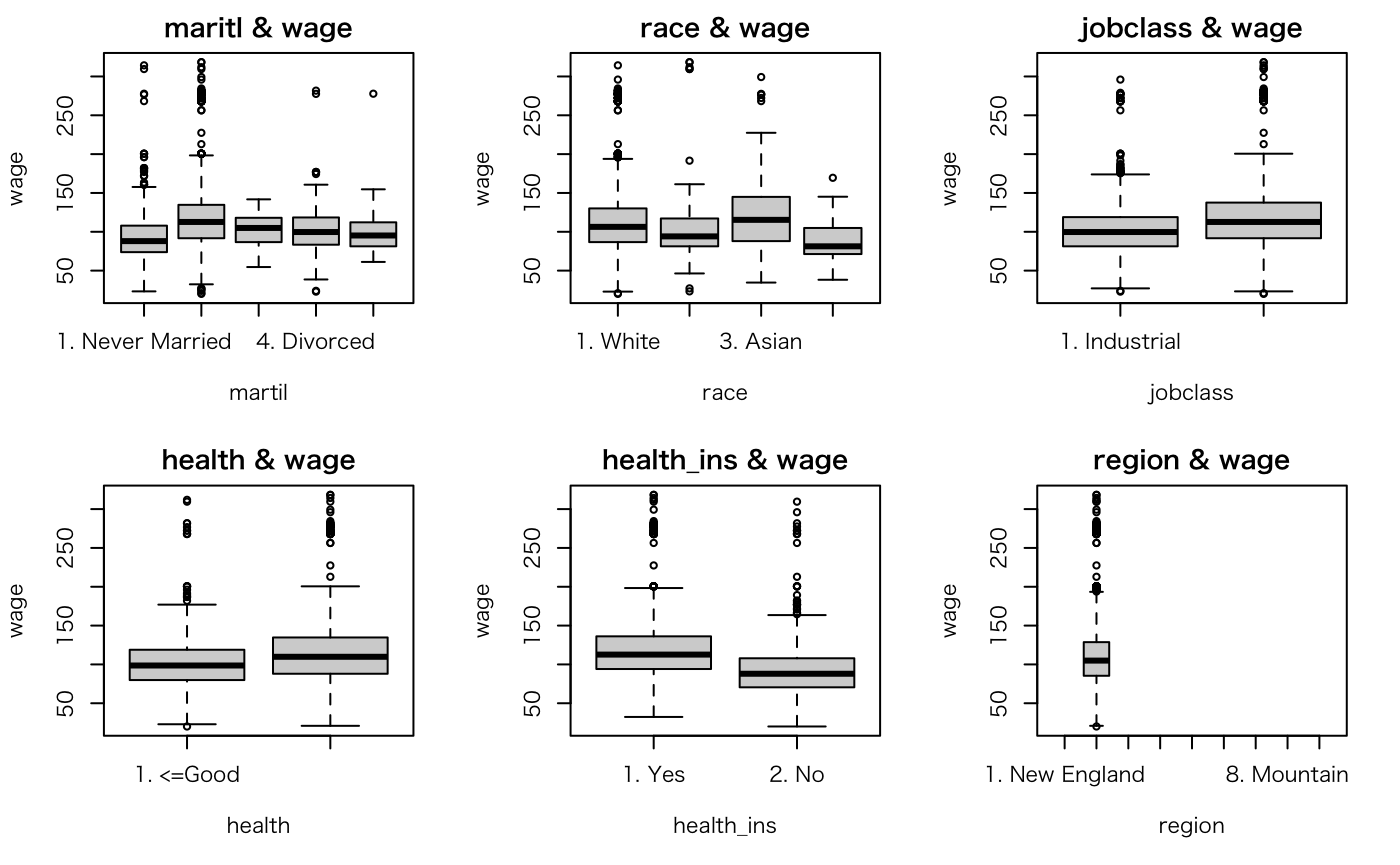
このプロットより、次の仮説を立てました。
- martil(婚姻状況)については、Married(既婚者)がWageが高い。
- race(人種)については、White(白人)とAsian(アジア人)がWageが若干高い。
- jobclass(職種)については、Information(情報産業系)がWageが高い。
- health(健康状態)については、>=Very Good(非常に良い人)がWageが高い。
- health_ins(保険加入の有無)については、Yes(加入者)がWageが高い。
regionについては、helpにもmid-atlantic onlyとは書いてありますが、データを見ても1地域しかないので、今回は考慮外にします。
gamライブラリで一般化加法モデルを作ってANOVAで検定する。
では、ANOVAを使ってGAMでの説明変数の有用性を確認します。
ここでは、「帰無仮説=モデルAがデータを十分に説明しているという、対立仮説=より複雑なモデルBが必要である」を設定します。
ANOVAを使うときは変数が入れ子になっていることが重要な点に気をつけます。
例えば、AとBのモデルを検定する場合は、Aに含まれる変数はBに全て含まれている必要があるということです。
今回は、education->maritl->jobless->health->health_ins->raceという順番で説明変数を増やしてGAMモデルを作りANOVAで検定してみます。
※先も書いた通り、yearとageはこの教科書で既に触れられているので、今回は考慮外とし、GAMモデル生成時にははじめから格納するものとします。また、yearとageは自然スプラインを用いてそれぞれ非線形関数を当てはめています。
では、先からの続きで実際にやってみます。
## gamでモデルを作って、ANOVAより良いモデルを選択する。
library(gam)
gam.fit01 <- gam(wage ~ year + s(age, 5) + education)
gam.fit02 <- gam(wage ~ year + s(age, 5) + education + maritl)
gam.fit03 <- gam(wage ~ year + s(age, 5) + education + maritl + jobclass)
gam.fit04 <- gam(wage ~ year + s(age, 5) + education + maritl + jobclass + health)
gam.fit05 <- gam(wage ~ year + s(age, 5) + education + maritl + jobclass + health + health_ins)
gam.fit06 <- gam(wage ~ year + s(age, 5) + education + maritl + jobclass + health + health_ins + race)
anova(gam.fit01, gam.fit02, gam.fit03, gam.fit04, gam.fit05, gam.fit06)
Analysis of Deviance Table
Model 1: wage ~ year + s(age, 5) + education
Model 2: wage ~ year + s(age, 5) + education + maritl
Model 3: wage ~ year + s(age, 5) + education + maritl + jobclass
Model 4: wage ~ year + s(age, 5) + education + maritl + jobclass + health
Model 5: wage ~ year + s(age, 5) + education + maritl + jobclass + health +
health_ins
Model 6: wage ~ year + s(age, 5) + education + maritl + jobclass + health +
health_ins + race
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 2989 3693842
2 2985 3599643 4 94198 < 2.2e-16 ***
3 2984 3585383 1 14260 0.0003988 ***
4 2983 3554455 1 30928 1.843e-07 ***
5 2982 3395637 1 158819 < 2.2e-16 ***
6 2979 3388299 3 7338 0.0915803 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
この結果、gam.fit06のraceまで説明変数を増やして複雑にする必要はなさそうですので、gam.fit05(説明変数: education, maritl, jobclass, health, health_ins)を採用します。
当てはめたGAMモデルを可視化から解釈する
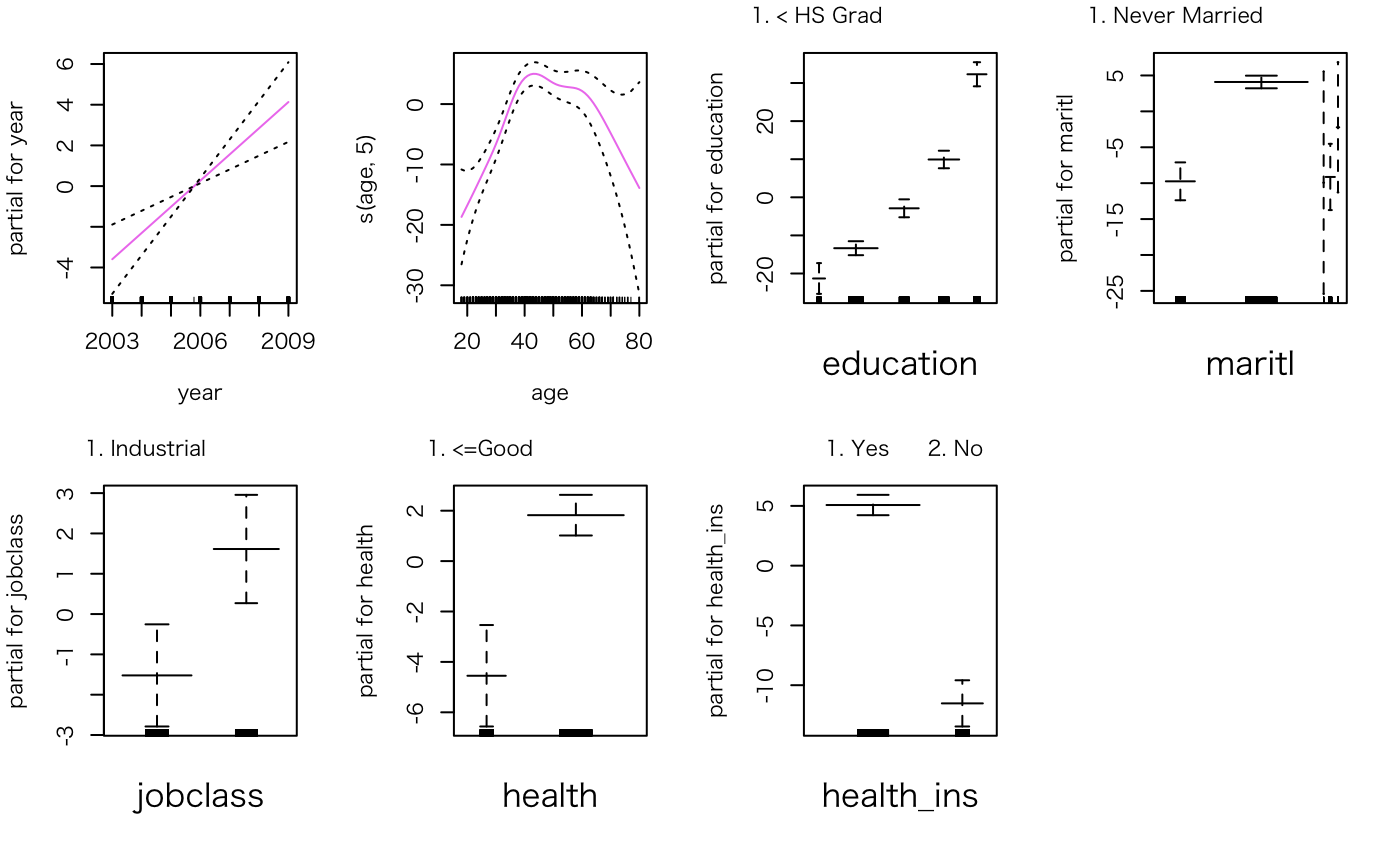
説明変数単位でWageの説明状況を可視化することができます。これはシンプルにplotで見ることができます。(実際はplot.Gamが呼ばれている)
par(mfrow=c(2,4))
plot(gam.fit05, se=T, col="violet")
ここで、maritlに注目すると、信頼区間が広すぎるカテゴリがあります。これは、いちばんはじめのSummaryの結果からもわかるのですが、データ量が該当区間だけ少なすぎるためこのような事態になっています。
1. Never Married 2. Married 3. Widowed 4. Divorced 5. Separated
648 2074 19 204 55
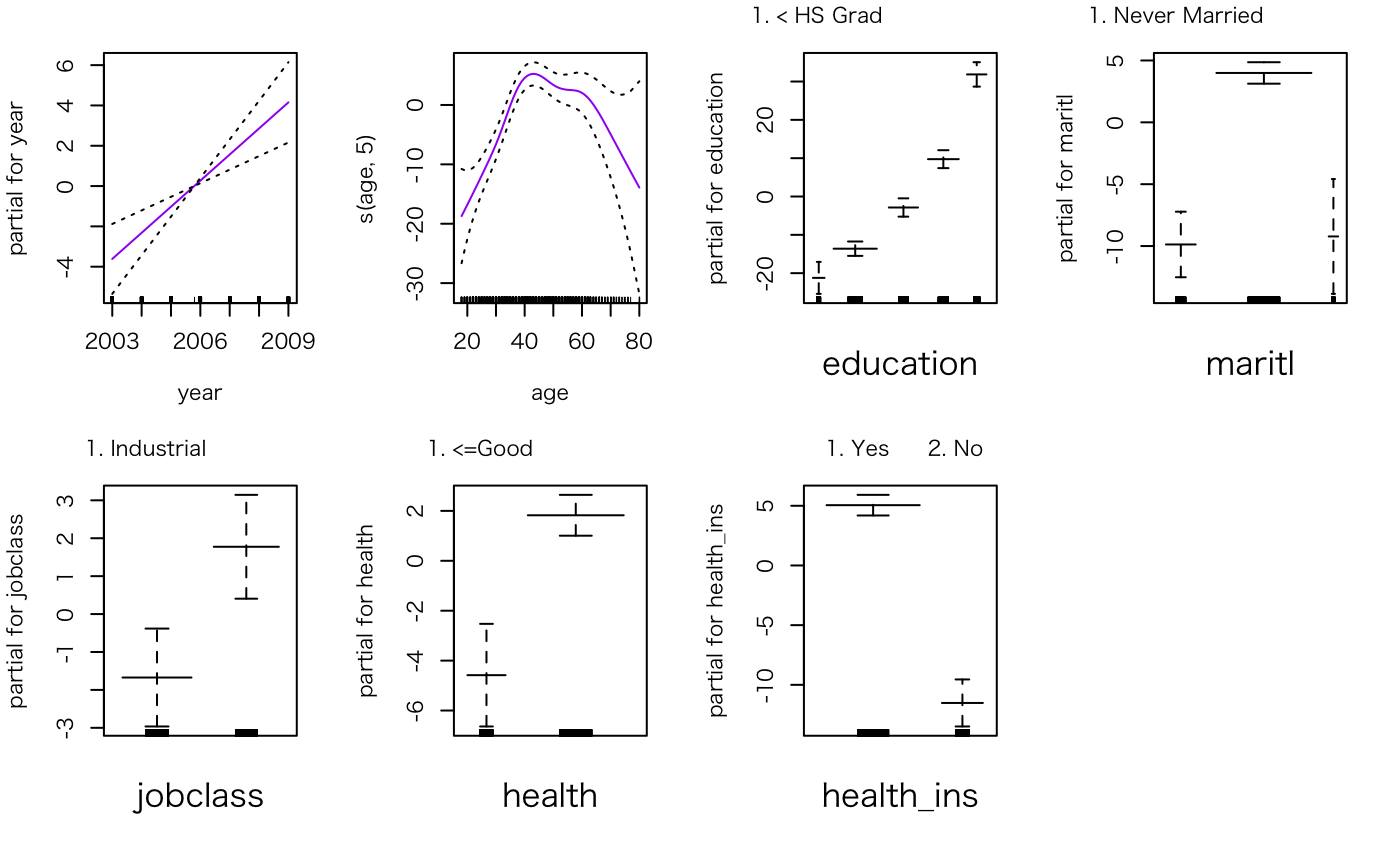
なので、極端に少ないWidowed(未亡人)、Separated(別居)を除いてモデルを再作成し、同様にプロットしてみます。
gam.fit05.sub <- gam(wage ~ year + s(age, 5) + education + maritl + jobclass + health + health_ins, data=Wage, subset=(maritl!="3. Widowed" & maritl!="5. Separated"))
par(mfrow=c(2,4))
plot(gam.fit05.sub, se=T, col="purple")
maritlについては、Divorced(離婚)も除いても良かったかもですが、今回はこのままにしておきます。
で、各変数の解釈ですが、このプロットのみた通りにできまして、
- yearについては、年が経つにつれ、賃金が線形に高くなる傾向がある。
- ageについては、40代前後が最も賃金が高い。そこから離れると賃金は低くなる傾向にある。
- educationについては、学歴が高いほど賃金は高い傾向がある。
- maritlについては、既婚者の方が賃金は高い傾向がある。
- jobclassについては、industrialよりもinformationの方が賃金が高い傾向がある。
- healthについては、良い方が賃金が高い傾向がある
- health_insについては、保険加入者の方が賃金が高い傾向がある。
というふうに、変数ごとに状況が見れるので、解釈がしやすい→推論向きの手法ということになります。
あと、基本的なことではありますが、これらの変数が賃金を上げる原因になっているとは言えないことに注意が必要です。
例えば、保険加入については、「加入したから賃金が上がったというよりも、高い賃金で余裕があるから保険に加入できる」と考えた方が妥当では?ということです。
結果からどこまで言えるのかは、きちんと把握した上で理解し活用しないといけないですね。
PythonでGAMを使う
pyGAMで利用可能のようなので、QuickStartに倣ってそのまま動かしてみます。
なお、私はMacOSにてVS Codeを動かし、その上でipynbファイルを作って動かしてます。
(VSCodeはリモートデバッグなども含めてどんどん便利になっているので、個人的には好きなエディタになっています。)
pyGAMのインストール
難しいことはなく、単にpipでinstallするだけです。
これを使うにあたり、pandasやmatplotlibも必要とあるので、無い人は次のようについでに入れておきます
pip3 install pygam pandas matplotlib
モデル作成
まずwageデータはこちらでも使えて、pyGAMの中に入っているので、ロードします。
from pygam.datasets import wage
X, y = wage()
で、続けてGAMでの回帰をします。
0番目変数(year)と1番目変数(age)をスプラインに、2番目変数(education)は質的変数をダミー変数にしてGAMの回帰モデルを作ります。
その後、summaryでモデルの当てはめを確認します。
from pygam import LinearGAM, s, f
gam = LinearGAM(s(0) + s(1) + f(2)).fit(X, y)
gam.summary()
LinearGAM
=============================================== ==========================================================
Distribution: NormalDist Effective DoF: 25.1911
Link Function: IdentityLink Log Likelihood: -24118.6847
Number of Samples: 3000 AIC: 48289.7516
AICc: 48290.2307
GCV: 1255.6902
Scale: 1236.7251
Pseudo R-Squared: 0.2955
==========================================================================================================
Feature Function Lambda Rank EDoF P > x Sig. Code
================================= ==================== ============ ============ ============ ============
s(0) [0.6] 20 7.1 5.95e-03 **
s(1) [0.6] 20 14.1 1.11e-16 ***
f(2) [0.6] 5 4.0 1.11e-16 ***
intercept 1 0.0 1.11e-16 ***
==========================================================================================================
Significance codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Sig.Codeの結果を見る限り、ひとまずこの説明変数の採用に問題なさそうなので進めます。
また、スプライン数を指定したい場合はn_splinesで指定できます。(デフォルト20の模様)
gam = LinearGAM(s(0, n_splines=5) + s(1) + f(2)).fit(X, y)
自動チューニング
L2のリッジ罰則を使って自動チューニングをします。
このパラメータλをクロスバリデーションで決めるためにgrid searchを次のようにできるようです。
(なお、先ほどのlambdaは全て0.6でした。先のsummary結果参照)
lam = np.logspace(-3, 5, 5) #ログスケールに均等な配列を生成
lams = [lam] * 3
gam.gridsearch(X, y, lam=lams)
gam.summary()
100% (125 of 125) |######################| Elapsed Time: 0:00:03 Time: 0:00:03
LinearGAM
=============================================== ==========================================================
Distribution: NormalDist Effective DoF: 9.2948
Link Function: IdentityLink Log Likelihood: -24119.7277
Number of Samples: 3000 AIC: 48260.0451
AICc: 48260.1229
GCV: 1244.089
Scale: 1237.1528
Pseudo R-Squared: 0.2915
==========================================================================================================
Feature Function Lambda Rank EDoF P > x Sig. Code
================================= ==================== ============ ============ ============ ============
s(0) [100000.] 5 2.0 7.54e-03 **
s(1) [1000.] 20 3.3 1.11e-16 ***
f(2) [0.1] 5 4.0 1.11e-16 ***
intercept 1 0.0 1.11e-16 ***
==========================================================================================================
Significance codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
より高次元なサーチをしたければ、randomized searchをすれば良いとのこと。np.randam.randを使って、探索対象のλを設定してgrid searchします。
また、その結果をsummaryで見て、さらに先のモデルとのGCVスコアで比較してみます。
lams = np.random.rand(100, 3) # random points on [0, 1], with shape (100, 3)
lams = lams * 6 - 3 # shift values to -3, 3
lams = 10 ** lams # transforms values to 1e-3, 1e3
random_gam = LinearGAM(s(0) + s(1) + f(2)).gridsearch(X, y, lam=lams)
random_gam.summary()
gam.statistics_['GCV'] < random_gam.statistics_['GCV']
100% (100 of 100) |######################| Elapsed Time: 0:00:04 Time: 0:00:04
LinearGAM
=============================================== ==========================================================
Distribution: NormalDist Effective DoF: 13.1861
Link Function: IdentityLink Log Likelihood: -24117.6384
Number of Samples: 3000 AIC: 48263.6491
AICc: 48263.7935
GCV: 1246.1467
Scale: 1236.2915
Pseudo R-Squared: 0.2929
==========================================================================================================
Feature Function Lambda Rank EDoF P > x Sig. Code
================================= ==================== ============ ============ ============ ============
s(0) [630.5703] 20 5.3 8.23e-03 **
s(1) [477.5545] 20 4.0 1.11e-16 ***
f(2) [0.1096] 5 3.9 1.11e-16 ***
intercept 1 0.0 1.11e-16 ***
==========================================================================================================
Significance codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
True
今回はrandomized searchの方が結果が良かったです。計算負荷の問題がなければ、なるべくrandomized searchをやってみる方が良さそうですね。
また、statistics_で他のスコアも参照できるので、目的に沿ったスコアを確認するのが良さそうです。
list(gam.statistics_.keys())
['n_samples',
'm_features',
'edof_per_coef',
'edof',
'scale',
'cov',
'se',
'AIC',
'AICc',
'pseudo_r2',
'GCV',
'UBRE',
'loglikelihood',
'deviance',
'p_values']
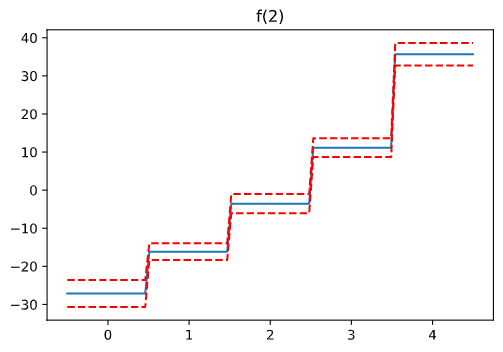
プロットの結果確認
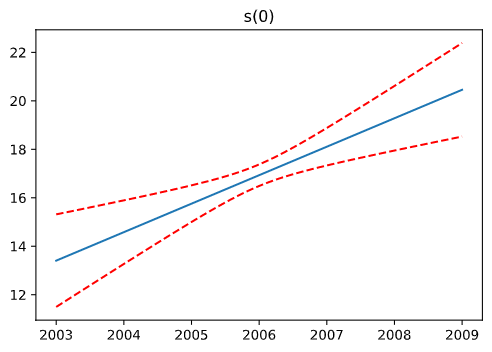
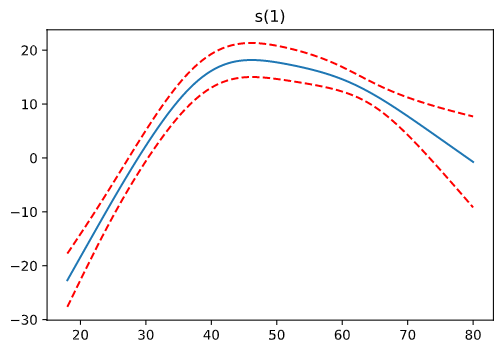
Rでもやった変数ごとのプロットについては、次のように確認できるようです。
import matplotlib.pyplot as plt
for i, term in enumerate(gam.terms):
if term.isintercept:
continue
XX = gam.generate_X_grid(term=i)
pdep, confi = gam.partial_dependence(term=i, X=XX, width=0.95)
plt.figure()
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(repr(term))
plt.show()
駆け足でしたが、ひとまずQuickStartの内容が終わりました。
最後に
駆け足ですが、一通り使ってみました。
線形モデルを拡張した一般化加法モデル(GAM)は、うまく使える場面もありそうなので、実問題に応用していきたいです。
実行環境
- OS
- ・macOS Catalina 10.16.17
- Rに関する環境
- ・R 4.0.3 (2020-10-10)
- ・RStudio 1.3.1093
- ・gam 1.20
- Pythonに関する環境
- ・Python 3.9.0
- ・Visual Studio Code 1.51.1
- ・Jupyter 1.0.0
- ・pyGAM 0.8.0