円周率は本当に3.14・・・なのか？

前提

この記事は限界開発鯖 Advent Calendar 2020の9日目です。
8日目:謎のコミュニティ「限界開発鯖」を支える技術
10日目:Arduinoと筋電センサMyoWareで始める筋電計測

厳密性に欠けた説明がされてる場合があります。極力、気をつけてはいますが何かありましたらコメントかTwitterまでお願いします。

円周率とは？

さて、そもそも円周率について理解していますか？
大体、小５くらいに円周率3.14のことを習い、中学生で$\pi$を習ったと思います。

円周率の求め方について復習してみましょう。
円周率は
「円の円周の長さ」÷　「直径の長さ」
で求めることができます。

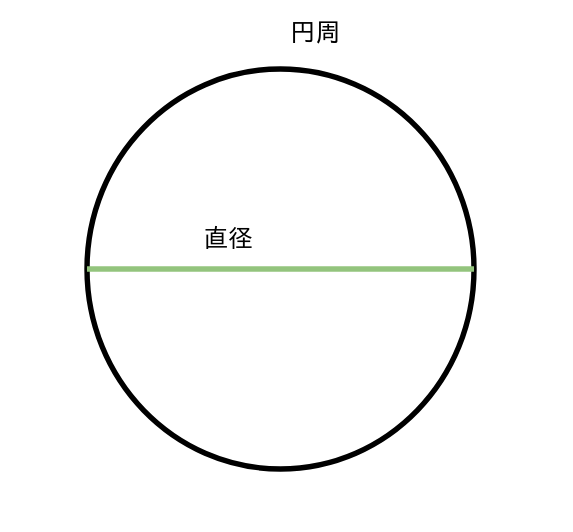
円周率は数学に限らず、物理や工学系で使われているので、最も重要な数学定数とも言われています。¹
ちなみに、円周率は無理数でもあり、超越数でもあります。
超越数とは、$f(x)=0$となる$n$次方程式$f$がつくれない$x$のことです。
詳しい説明は過去の記事(√2^√2 は何？)に書いてありますので、気になる方は読んでみてください。

近似して求める。

アルキメデスの方法

まずは、手計算で求めてみましょう。最初に、アルキメデスの方法を使って求めてみます。
アルキメデスの方法では、
円に内接する正$n$角形と外接する正$n$角形を使います。
以下に$r=1,n=6$の図を示します。²
(青が円に内接する正6角形、緑が円に外接する正6角形です)

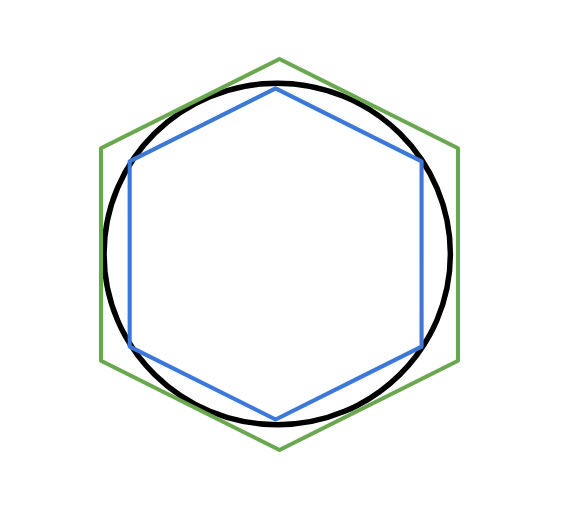
そうすると、
$内接する正n角形の周の長さ < 円周 < 外接する正n角形の周の長さ$
となります。
$n=6$のとき、内接する正6角形の周の長さを$L_6$、外接する正6角形の周の長さを$M_6$とし、全体を2倍すると、
$2L_6 < 2\pi < 2M_6$
となります。これを2で割れば、
$L_6 < \pi < M_6$
となり、$\pi$を求めることができます。

もちろん、$n$が大きくなれば、範囲は狭くなるので、
$L_6 < L_n < \pi < M_n < M_6$
となります。
このようにして、円周率を求めていきます。アルキメデスは正96角形を用いて、
$3\frac{10}{71} < \pi < 3\frac{1}{7}$
を証明しています。
証明など気になる方は以下のサイトをおすすめします。
アルキメデスと円周率
第28回　円周率を数えよう（後編）
ここで、
$3\frac{10}{71}$は3.140845...
$3\frac{1}{7}$は3.1428571...
となります。

すなわち、$3.140845... < \pi < 3.1428571...$となり、僕たちが知っている円周率の値3.14と一致しますね！
よって、円周率は3.14...と言えそうです！

#これで終わりはつまらない
3.14...となるのはわかりました。
ただ、僕たちが知りたいのは、...のところです。
3.141592...と暗記をしたあの頃は無駄な時間ではなかったのか
不安がよぎるので、ほかの方法でもっと正確に求めてみましょう。

ということで、以下に方法を示します。

逆正接関数

$$tan^{-1}1 = \frac{\pi}{4}$$
を利用して
$$\pi = 4tan^{-1}1$$
とすると円周率が求まります。

ライプニッツの公式

$$1-\frac{1}{3} + \frac{1}{5} -\frac{1}{7} + \dots =\sum_{n=1}^\infty\frac{(-1)^{n-1}}{2n-1}= \frac{\pi}{4}$$
を利用して求めます。

ライプニッツの公式自体は、フーリエ級数³などで求めることができます。

今回はフーリエ級数から求めてみましょう。
以下の関数を考えてみましょう。

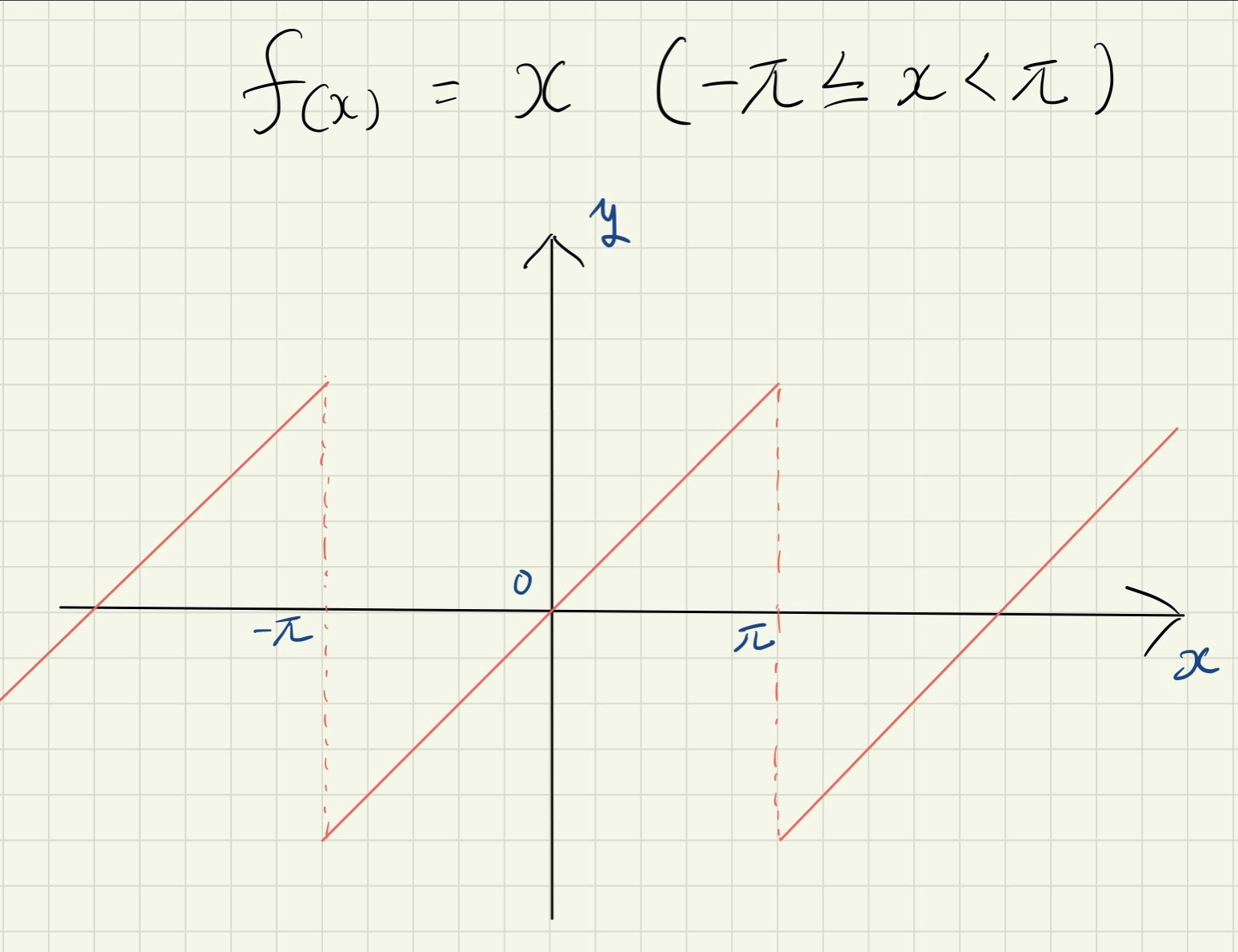
$[-\pi:\pi]$の周期的な関数です。

まずは、こいつをフーリエ級数に展開してみましょう。

フーリエ級数で展開すると、\\
f(x) \simeq \frac{a_0}{2}+ \sum_{n=1}^{\infty}a_ncos(nx) + b_nsin(nx)\\
f(x) = x は奇関数より、a_0 = a_n = 0\\
f(x) \sim \sum_{n=1}^{\infty}b_nsin(nx)\\
よって、\\

b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}xsin(nx)dx
= \frac{1}{\pi}[\frac{sin(nx)}{(n)^2}-\frac{xcos(nx)}{n}]_{-\pi}^{\pi}\\
=\frac{1}{\pi}((-\frac{1}{n})\pi cos(n\pi)-(-\pi)cos(-n\pi))\\
=\frac{-2}{n}cos\pi\\
=\frac{2(-1)^{n+1}}{n}\\

ここまでがフーリエ級数を求める方法です。

x = \frac{\pi}{2}を代入すると、\\
f(\frac{\pi}{2}) = \frac{\pi}{2} = 2\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}sin\frac{n\pi}{2}\\
より、\\
\frac{\pi}{4} = \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}sin\frac{n\pi}{2}\\
ここで、sin\frac{n\pi}{2}のnの値を1,2,3...と上げてみると\\
n = 1のとき1\\
n = 2のとき0\\
n = 3のとき(-1)\\
n = 4のとき0\\
n = 5のとき1\\
\vdots\\
となる。
よって、\\
\sum_{n=1}^\infty\frac{(-1)^{n-1}}{2n-1}= \frac{\pi}{4}

こうして、ライプニッツの公式を求めることができました！
ちなみに、三角関数の直交性⁴などを使って計算を簡単にできるので、テクニックとして覚えておいてください。

バーゼル級数

1+\frac{1}{2^2}+\frac{1}{3^2}+\dots=\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6} 

を利用して求めることもできます。

マチンの公式

$$\pi = 16 tan^{-1}\frac{1}{5} - 4tan^{-1}\frac{1}{239}
$$
を利用します。
また、
$$
f(m) = 16\sum_{n=0}^{3m+2}\frac{(-1)^n}{2n+1}(\frac{1}{5})^{2n+1} - 4\sum_{n=0}^m\frac{(-1)^n}{2n+1}(\frac{1}{239})^{2n+1}
$$
ともなります。
マチンの公式に似た公式は大量に知られています。

例えば、オイラーが見つけた
$$\frac{\pi}{4}=5tan^{-1}\frac{1}{7} - 2tan^{-1}\frac{3}{79}$$
や
詩人の高野喜久雄が見つけた
$$\frac{\pi}{4}=12tan^{-1}\frac{1}{49} + 32tan^{-1}\frac{1}{57}-5tan^{-1}\frac{1}{239} +12tan^{-1}\frac{1}{110443}$$
もあります。

ラマヌジャンの公式

個人的に一番好きです。

$$
\frac{1}{\pi} = \frac{2\sqrt{2}}{99^2}\sum_{n=0}^\infty\frac{(4n)!(1103+26390n)}{(4^n99^nn!)^4}
$$

というか、意味が分かりません。これで円周率が出てくるなんて思いつくわけがない。
けど、出てくるらしい。世界って不思議。

この公式使って2020年の1月25日に303日かけて50兆桁求めたらしいです。

##モンテカルロ法
円周率を求めると聞いて最初に思い浮かんだ方もいるのではないでしょうか？
モンテカルロ法を用いて、円周率を求めてみましょう。

まず、円の面積の求め方を復習しましょう。
円の面積をS、半径をrとすると、$S = \pi r^2$で求めることができます。
$\pi = \frac{S}{r^2}$となるので、Sとrを求めることができれば、$\pi$を求めることができます。
これを利用して求めてみましょう。

今回は$\frac{1}{4}$の半径rの円と1辺がrの正方形を考えます。
ランダムに点を打ち、円の内部の点と正方形内にある点の数を数えます。
(今回だと、円の内部に7個、正方形に9個あります)

これをたくさんの点をランダムに落としたら面積と考えてよいはずですね。

以上を踏まえて、求めてみます。

正方形の面積 : \frac{1}{4}の円の面積 = 正方形内にある点の数\alpha : 円の内部にある点の数\beta\\
となるので、\\
r^2 : \frac{1}{4}\pi r^2 = \alpha : \beta\\
よって\\
r^2\beta = \frac{1}{4}\pi r^2\alpha\\
\pi = 4\frac{\beta}{\alpha}

ということで、$4\frac{\beta}{\alpha}$で円周率を求められることがわかりました。

#実際にやってみた。
まず、基準となる値を決定しましょう。
みんな大好きNumpy君にpiの値を返す関数があるので、それを利用しましょう。
これを信用していいのかという話になると思いますが、そこは一旦許容しましょう。

import numpy as np
print(np.pi)

ということで、こいつを基準にして確認していきます。
それでは、実装してみましょう。

import numpy as np


class GetPi:

    #比較用
    def numpy_pi(self):
        print("Pi: {}".format(np.pi))
    #逆正接関数
    def arctan(self):
        print("Arctan_Pi: {}".format(4 * np.arctan(1)))

    #ライプニッツの公式
    def leibniz_formula(self, _n):
        x = np.arange(1, _n + 1)
        pi = np.sqrt(6 * np.sum(1 / x ** 2))
        print("Leibniz_Pi: {}".format(pi))

    # バーゼル級数
    def basel_series(self, _n):
        x = np.arange(1, _n + 1)
        a = 1 / (2 * x - 1)
        b = (-1) ** (x - 1)
        pi = 4 * np.dot(a, b)
        print("Basel_Pi: {}".format(pi))


    # マチンの公式
    def machin_like_formula(self, _n):
        X = 0.0
        for n in range(3*_n+2):
            a = ((-1)**n)
            b = 2*n + 1
            X += a/b * (1/5)**(2*n+1)

        Y = 0.0
        for n in range(_n):
            a = ((-1)**n)
            b = 2*n + 1
            Y += a/b * (1/239)**(2*n+1)
        print("Machin_Pi: {}".format((16*X) - (4*Y)))

    #ラマヌジャンの公式
    def ramanujan_series(self, _n):
        sum = 0.0
        for n in range(_n):
            a = np.math.factorial(4 * n) * (1103 + 26390 * n)
            b = (396**n * np.math.factorial(n))**4
            sum += a/b

        pi = (2*np.sqrt(2))/(99**2) * sum
        print("Ramanujan_Pi: {}".format((1/pi)))
    #モンテカルロ法
    def montecarlo_method(self, _n):
        alpha = _n
        beta = 0
        ran_x = np.random.rand(alpha)
        ran_y = np.random.rand(alpha)
        ran_point = np.hypot(ran_x, ran_y)

        for i in ran_point:
            if i <= 1:
                beta += 1

        pi = 4*beta/alpha
        print("MonteCalro_Pi: {}".format(pi))

n = 1000
pi = GetPi()
pi.numpy_pi()
pi.arctan()
pi.leibniz_formula(n)
pi.basel_series(n)
pi.machin_like_formula(n)
pi.ramanujan_series(5)
pi.montecarlo_method(n)

今回、n = 1000としています。
(ただし、ラマヌジャンの公式は5としています。)
以下、実行結果です。

Pi: 3.141592653589793
Arctan_Pi: 3.141592653589793
Leibniz_Pi: 3.1406380562059932
Basel_Pi: 3.140592653839791
Machin_Pi: 3.141592653589794
Ramanujan_Pi: 3.141592653589793
MonteCalro_Pi: 3.104

モンテカルロ法は収束が遅い(O($\frac{1}{\sqrt{n}}$)ので、あまり精度はよくありません。
一方、ラマヌジャンの公式はNumpy.piや逆正接関数の値と完全に一致しています。
最強です

先程、ラマヌジャンの公式のみn=5としましたが、ほかのやつもn=5でやってみましょう。
以下、実行結果です。

Pi: 3.141592653589793
Arctan_Pi: 3.141592653589793
Leibniz_Pi: 2.9633877010385707
Basel_Pi: 3.3396825396825403
Machin_Pi: 3.141592653589794
Ramanujan_Pi: 3.141592653589793
MonteCalro_Pi: 2.4

実行結果を見てわかる通り、ラマヌジャンの公式の収束が速いということがわかると思います。
やっぱり最強！

#最後に
紹介したのは、ほんの一部であり、またあまり証明を載せられていません。
できるだけ、証明は追記していきます。
もし、ほかに求め方が気になる方がいらっしゃいましたら、以下の記事をお勧めします。
(これを書いている途中に見つけてしまったが、目的が違うので許してください。)
【ハーレム】多すぎて選べない！Pythonで円周率πを計算する13の方法

無事、僕たちが青春を費やした円周率暗記の時間は無駄ではなかったですね！

少しでも面白いと思っていただけたら幸いです。
僕は少し簡単なお話にしましたが、他の方の技術力マシマシの記事を見てみてくださいね！

それでは、良い1日を。

1. 参考: Wikipedia 円周率 ↩

2. 温かい目で見てほしい ↩

3. 複雑な周期関数や周期信号をcosやsinなどの"単純な形の"周期性をもつ関数の無限の和によって表したもののことを指します。 ↩

4. $$\int_{-\pi}^{\pi}sin(nx)sin(mx)dx,\int_{-\pi}^{\pi}sin(nx)cos(mx)dx,\int_{-\pi}^{\pi}cos(nx)cos(mx)dx$$の3つの積分を考えます。計算過程は省略しますが、$\int_{-\pi}^{\pi}sin(nx)cos(mx)dx = 0$となり、$\int_{-\pi}^{\pi}sin(nx)sin(mx)dx = \int_{-\pi}^{\pi}cos(nx)cos(mx)dx$ はm=nのとき$\pi$,m$\neq$ nのとき0となります ↩