こちらはYuruvent Advent Calendar 2025 11日目の記事です。
はじめに
皆さん、人生を過ごしていると、グラムシュミットの正規直交化法について聞かれることありますよね。
私はあります。さて、なんでグラムシュミットの正規直交化法が成立するの?と聞かれたらあなたは答えられますか?
私は無理です。なので、この記事で追ってみましょう。
ただし、これはYuruventなので、厳密には追いません。許してください。
グラムシュミットの正規直交化法とは
$V$をベクトル空間とし、{$a_n$} $\subset V$をその基底とします。このとき、$n \in \mathbb{R}$とすると
\displaylines{x_n = a_n - \sum_{k=1}^{n-1}(a_n\cdot e_k)e_k\\e_n = \frac{x_n}{\|x_n\|}}
で構成される{$e_n$}は正規直交基底となります。
なぜこの式で直交するベクトルが求まるのかは、下の図を見れば直感的に理解できます。
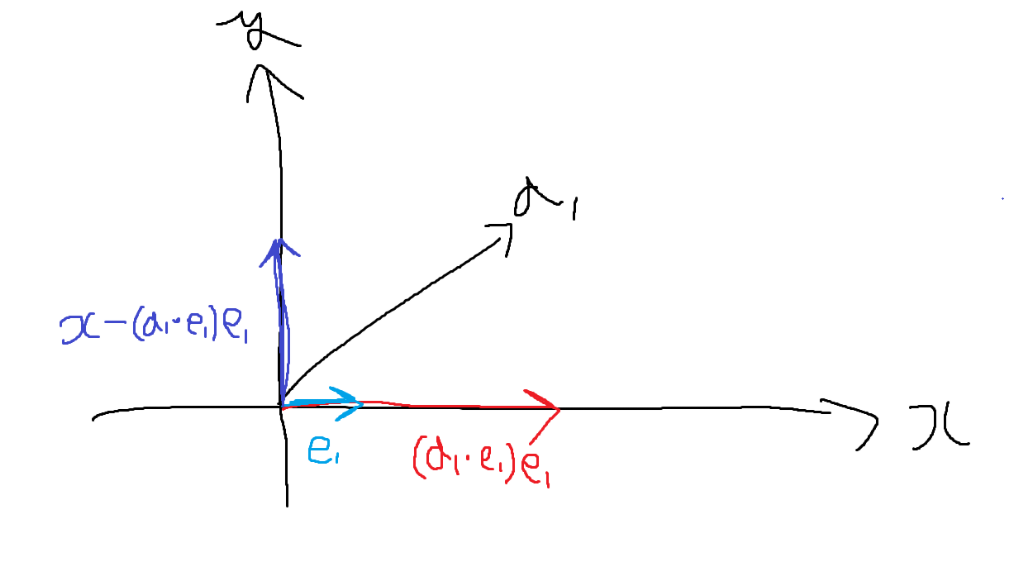
ベクトル$a_1$を、基底ベクトル$e_1$に沿った正射影ベクトル$(a_1\cdot e_1)e_1$とベクトル$a_1$の$e_1$と平行な成分を差し引けば、$x - (a_1\cdot e_1)$が垂直な成分と言えるでしょう。
このようにして、直交するベクトルを生成できます。
ここで、正規直交基底について説明します。
まず、「大きさが1である」かつ「互いに直交するベクトル」の集まりを正規直交系と言います。しかし、この定義のみだと空間全体を張っているか不明です。
よって、正規直交基底とは、「各ベクトルの長さが 1 で、互いに直交しているベクトルたち(正規直交系)が、その空間の基底になっているもの」をいいます。
具体例を考えてみましょう。
$e_1=(1,0)$, $e_2 = (0,1)$とします。これは、大きさが1かつ互いに直交することは図に書けばすぐわかります。
そして、任意の$(x,y)$が$(x,y) = xe_1 + ye_2$と表せるため、これは$\mathbb{R}^2$の正規直交基底であるといえます。
正規直交基底であることの証明
大きさが1なのは
\displaylines{e_n = \frac{x_n}{\|x_n\|}}
より明らかです。
よって、$e_n$が他のベクトルと直交することを示せばよいです。
$e_1, \dots, e_n$が直交すると仮定する。
$1\leq i \leq n-1$のとき、
\displaylines{x_n\cdot e_i &=& (a_n - \sum_{k=1}^{n-1}(a_n\cdot e_k)e_k)\cdot e_i\\ &=& a_n\cdot e_i - \sum_{k=1}^{n-1}(a_n\cdot e_k)(e_k\cdot e_i)\\ &=&(a_n\cdot e_i) - (a_n\cdot e_i) = 0}
より、$x_n$が他のベクトルと垂直することがわかります。
以上より、$e_n$が他のベクトルと直交することが示せました。
プログラム
これだけだと物足りないので、Pythonで実装してみましょう。
Pythonで実装すると以下のようになります。
import numpy as np
def gram_schmidt(vectors):
orthonormal_vectors = []
vectors = np.array(vectors, dtype=np.float64)
for v in vectors:
for u in orthonormal_vectors:
v -= np.dot(v, u) * u
v /= np.linalg.norm(v)
orthonormal_vectors.append(v)
return orthonormal_vectors
実際にあっているか計算してみましょう。
例えば、$a_1=(1, 2), a_2=(2, 1)$としましょう。
上記の式に代入して$e_1$を求めてみると、
\displaylines{x_1 = a_1 = (1, 2)\\ e_1 = \frac{x_1}{\|x_1\|} = \frac{1}{\sqrt{5}}(1, 2)\\}
となります。同様に$e_2$を求めると、
\displaylines{x_2 = a_2 - (a_2\cdot e_1)e_1 = (2,1) - \left(\frac{4}{\sqrt{5}}\right)\frac{1}{\sqrt{5}}(1, 2)=(2,1) - \frac{4}{5}(1,2) = \left( \frac{6}{5}, -\frac{3}{5}\right)\\e_2= \frac{x_2}{\|x_2\|} = \frac{1}{\sqrt{5}} (2, -1)}
ということで、$e_1,e_2$は
e_1=\frac{1}{\sqrt{5}}(1, 2), \space e_2 = \frac{1}{\sqrt{5}} \left(2, -1\right)
となります。それでは、実際に計算してみましょう。
import numpy as np
def gram_schmidt(vectors):
orthonormal_vectors = []
vectors = np.array(vectors, dtype=np.float64)
for v in vectors:
for u in orthonormal_vectors:
v -= np.dot(v, u) * u
v /= np.linalg.norm(v)
orthonormal_vectors.append(v)
return orthonormal_vectors
A = [np.array([1, 2]), np.array([2, 1])]
orthonormal_A = gram_schmidt(A)
for vec in orthonormal_A:
print(vec)
[0.4472136 0.89442719]
[ 0.89442719 -0.4472136 ]
以上の結果から、Pythonプログラムでも求めることができました。
終わりに
グラムシュミットの正規直交化法について聞かれたら、これで答えられますね。