[python] バスの渋滞予測モデルの精度向上をしてみる

はじめに

初めまして。Aidemyでデータ分析を学んでいるものです。
現在、自動車部品メーカーで機械の設計をしていますが、データ分析のスキルを身につけたく
ディープラーニングにも触れたいと思い学習をしています。

今回は半年間の学びの成果物として本記事を作成しました。
至らぬ箇所も多々あるかと思いますが、暖かいご指摘やコメントいただければ幸いです。

環境

・Python 3.9.16
・pandas 1.3.5
・keras 2.11.0
・tslearn 0.5.3.2

目的

本記事では、@N_H_tennis殿の記事
“[python] バスのGPSデータを時系列データとして処理し道路状況（渋滞）を予測してみる”
に対して、渋滞の予測精度を向上させるため、バス停の位置で停車している場合を取り除き効果を確認します。

参考記事：https://qiita.com/N_H_tennis/items/3aa98ff40defcee1bbb1

実施手順

1.参考とする記事を正しく再現できるか確認する。
　また、正しく再現できない場合は修正を加える。

　扱うデータはkaggleのジャカルタ市内のバスのGPSデータを使用
https://www.kaggle.com/datasets/rasyidstat/transjakarta-bus-gps-data

2.1.で再現ができたら、データの緯度経度の範囲内にあるバス停の
　緯度経度情報をGoogle MAPから抽出。
　このバス停の緯度経度から一定範囲内にあるデータにフラグをつける。
　緯度経度の抽出にはGoogle MAP APIを使用する。
　
　公式HP：https://developers.google.com/maps/?hl=ja

3.バス停の位置に付近のデータを除外して再度学習を行い、
　モデル精度や渋滞発生位置の変化について考察を行う。

　kapler.gl：https://note.com/kazukio/n/n3407e34d2985

それでは以下より実施手順の詳細に入りたいと思います。

1.参考記事の再現（渋滞予測）

①データの確認・前処理

前述の通りkaggle内にあるデータセット：Transjakarta Bus GPS Data( https://www.kaggle.com/rasyidstat/transjakarta-bus-gps-data )を用いて学習を行います。
このデータは、2019年11月26日の14時から18時の間に、インドネシアの首都ジャカルタ走行したバスのGPSを30秒毎に取得したデータです。

まずはデータを確認します。

read.py

import pandas as pd

gps_data = pd.read_csv('/content/drive/MyDrive/transjakarta_gps.csv')
gps_data.head()

緯度経度の位置情報と時間のデータはありますが、速度データはないため作成が必要となることがわかります。

次に欠損値の確認を行います。

check data.py

print(len(gps_data))
print(gps_data.isnull().sum())

緯度と経度の情報数は多く含まれているためデータとして問題なさそうです。

次に、numpy配列にして、時間変化・変位・時速の情報を追加していきます。

data preprocessing.py

import numpy as np

#np.arrayの配列を作成
bus_trip_gps = gps_data[["bus_code", "trip_id","gps_datetime", "longitude", "latitude"]]
bus_gps = bus_trip_gps.values

display(bus_gps)

#距離の変位を調査する
bus_gps_plus = np.vstack((np.zeros(2).reshape(1,2), bus_gps[:, 3:5]))
bus_gps_minus = np.vstack((bus_gps[:, 3:5], np.zeros(2).reshape(1,2)))
delta_bus_gps = bus_gps_plus - bus_gps_minus
delta_bus_gps = delta_bus_gps[1:,:]

display(delta_bus_gps)

#直感的に異常値に気付けるように単位をkmにする
delta_bus_gps*=110.94297

#距離のデータを作成
delta_distans = (np.square(delta_bus_gps[:,0:1]) + np.square(delta_bus_gps[:, 1:2]))**0.5

#時間の変化のデータを作成
bus_time_minus = pd.to_datetime(bus_gps[:-1,2:3].reshape(-1))
bus_time_plus = pd.to_datetime(bus_gps[1:,2:3].reshape(-1))
delta_time_gps = bus_time_plus - bus_time_minus
delta_time_gps = delta_time_gps/np.timedelta64(1,'s')
delta_time_gps = np.array(delta_time_gps, dtype='float')
delta_time_gps = np.append(delta_time_gps,0)
delta_time_gps = delta_time_gps.reshape(len(delta_time_gps),1)

display(delta_time_gps)

#変化量、速度を時速になおす
delta_bus_gps /= (delta_time_gps + 1e-8)/(60*60)
delta_distans /= (delta_time_gps + 1e-8)/(60*60)

#bus_gpsに変位と距離を追加する
bus_gps = np.insert(bus_gps,[5] , delta_bus_gps, axis=1)
bus_gps = np.insert(bus_gps,[7] , delta_distans, axis=1)
bus_gps = np.insert(bus_gps,[3] , delta_time_gps, axis=1)

display(bus_gps)

次に、時系列データの作成をします。参考とするブログと同じく、5つの連続するデータを1つの時系列にまとめ、約150秒のデータとします。
trip_idとbus_codeが違うものは別々の時系列データとなるように処理します。

#5回の測定で一回の時系列データとする
#bus_codeとtrip_idで別々の時系列のデータとなるようにする。

gps_input_data=[]
gps_correct_data =[]

len_sequence = 5             # 時系列の長さ

bus_gps[:,0:2] = bus_gps[:,0:2].astype(np.str)
bus_code_list = np.unique(bus_gps[:,0:1])

for i in range(len(bus_code_list)): 
    bus_code = bus_code_list[i]
    bus_code_gps = bus_gps[np.any(bus_gps==bus_code,axis=1)]

    trip_id_list =np.unique(bus_code_gps[:,1:2])

    if i%100 == 0:
        print(i)

    for j in range(len(trip_id_list)):    
        trip_id =  trip_id_list[j]
        trip_id_gps = bus_code_gps[np.any(bus_code_gps[:,1:2]==str(trip_id),axis=1)]

        if len(trip_id_gps)>(len_sequence+2):
            for k in range(len(trip_id_gps)-(len_sequence+2)):
                gps_input_data.append(trip_id_gps[k:k+len_sequence,2:])
                gps_correct_data.append(trip_id_gps[k+len_sequence:k+(len_sequence+1),2:].reshape(7))


#インプット用のデータ                
#axis0 データ、axis1 同一データ内の時系列位置 axis2 時間、時間変化、緯度,経度,緯度方向変位(km),経度方向変位(km),時速(km/h)
gps_input_data=np.array(gps_input_data) 

#正解用のデータ
#axis0 データ、axis1 時間、時間変化、緯度,経度,緯度方向変位(km),経度方向変位(km),時速(km/h)
gps_correct_data =np.array(gps_correct_data)

モデルにインプットするデータ、正解用のデータ作成が完了しました。

②異常値の削除

異常値の削除を行なっていきます。削除するデータは以下3つです。

1、時速が150km/hを越えているもの
2、時系列内で移動がほとんどないもの
3、データをおおよそ30秒毎に取得できていないもの

以下実行コードです。

cleansing.py

#異常な値の削除
#正解の時速が150kmを超えているものを異常とみなす

high_distans_index0 = np.where(gps_input_data[:,:,-1]>150)
high_distans_index0 = high_distans_index0[0]

high_distans_index1 = np.where(gps_correct_data[:,-1]>150)
high_distans_index1 = high_distans_index1[0]

error_data_index=np.concatenate([high_distans_index0, high_distans_index1])
error_data_index=np.unique(error_data_index)

gps_input_data2 = np.delete(gps_input_data,error_data_index,axis=0)
gps_correct_data2 = np.delete(gps_correct_data,error_data_index,axis=0)

#データの時系列内での（1個目と5個目）移動距離が0.01km以下のものを異常とする

index_destans0 = np.where(((gps_input_data2[:,:,4].sum(axis=1)**2 + gps_input_data2[:,:,5].sum(axis=1)**2)**0.5) < 0.01)
index_destans0 = np.array(index_destans0)
index_destans0 = index_destans0.reshape(-1)

gps_input_data2 = np.delete(gps_input_data2,index_destans0,axis=0)
gps_correct_data2 = np.delete(gps_correct_data2,index_destans0,axis=0)

#時間の変位が25より小さい,35より大きいデータを異常とみなす

index_time_short0 = np.where(gps_input_data2[:,:,1]<25)
index_time_short0 = index_time_short0[0]
index_time_short1 = np.where(gps_correct_data2[:,1]<25)
index_time_short1 = index_time_short1[0]
index_time_short = np.concatenate([index_time_short0, index_time_short1])

index_time_long0 = np.where(gps_input_data2[:,:,1]>35)
index_time_long0 = index_time_long0[0]
index_time_long1 = np.where(gps_correct_data2[:,1]>35)
index_time_long1 = index_time_long1[0]
index_time_long = np.concatenate([index_time_long0, index_time_long1])

index_time_error = np.concatenate([index_time_long, index_time_short])
index_time_error = np.unique(index_time_error)

gps_input_data2 = np.delete(gps_input_data2,index_time_error,axis=0)
gps_correct_data2 = np.delete(gps_correct_data2,index_time_error,axis=0)

③LSTM（keras）を用いた速度の予測モデルの作成

リカレントネットワークの作成に入る前に、データの分割を行います。
データは以下の3つに分割します。
　・学習用：ネットワークの学習に用いる。
　・評価用：ネットワークの評価に用いる。
　　　　　過学習していないか、表現力が足りているかどうかの判断に用いる。
　・プロット用：学習後のモデルに対して、誤差を測定するデータに用いる。

各地点毎の標準的な速度をモデルに学習させるために、使用するデータは以下を用いることにしました。
　・時間変化
　・経度/経度
　・緯度経度から求めた速度

train_test_split.py

#データ分割用のインデックスの準備
np.random.seed(0)
all_data_number = len(gps_correct_data)
data_index =np.arange(all_data_number)
np.random.shuffle(data_index)

#時速データの準備
X = gps_input_data[:,:,(1,2,3,6)]
t = gps_correct_data[:,(1,2,3,6)]

#正規化
for i in range(len(t[0,:])):
    Xt_min = np.min((X[:,:,i].min(), t[:,i].min()))
    Xt_max = np.max((X[:,:,i].max(), t[:,i].max()))
    X[:,:,i] = (X[:,:,i]-Xt_min)/Xt_max
    t[:,i] = (t[:,i]-Xt_min)/Xt_max

#データの分割
train_data_number =(all_data_number*3)//5
plot_data_number = (all_data_number*1)//5

X_train = X[data_index[:train_data_number],:,:]
t_train = t[data_index[:train_data_number]]

X_test = X[data_index[train_data_number:(-plot_data_number)],:,:]
t_test = t[data_index[train_data_number:(-plot_data_number)]]

X_plot = X[data_index[(-plot_data_number):],:,:]
t_plot = t[data_index[(-plot_data_number):]]

次はモデルの構築です。
モデルの構築はkerasを使用します。
使用するリカレント層はLSTMを使用し、リカレントドロップアウトを使用して過学習を低減します。
誤差関数は誤差の速度を把握しやすい平均絶対誤差maeを使用します。

lstm.py

# LSTMを定義
import numpy as np
import pandas as pd

from keras.models import Sequential
from keras.layers import Dense, LSTM
from keras.optimizers import RMSprop

input_dim = 4                 # 入力データの次元数
output_dim = 1                # 出力データの次元数
num_hidden_units_1 = 64       # 隠れ層1のユニット数
num_hidden_units_2 = 32       # 隠れ層2のユニット数
batch_size = 1000             # ミニバッチサイズ
num_of_training_epochs = 200  # 学習エポック数

model = Sequential()
model.add(LSTM(num_hidden_units_1,
              input_shape=(len_sequence,input_dim),
              return_sequences = True,
              recurrent_dropout = 0.5))
model.add(LSTM(num_hidden_units_2,
              recurrent_dropout = 0.3))
model.add(Dense(output_dim))
model.compile(loss="mae", 
              optimizer=RMSprop())
model.summary()

ではモデルの学習を行います。

model.py

import matplotlib.pyplot as plt

#モデルの学習
history = model.fit(X_train, t_train[:,-1],
                  epochs = num_of_training_epochs,
                  batch_size = batch_size,
                  validation_data = (X_test,t_test[:,-1]))
#学習結果の可視化
plt.plot(range(num_of_training_epochs),history.history["loss"], 'bo',color='red', label='Training loss',markersize=3)
plt.plot(range(num_of_training_epochs),history.history["val_loss"], 'b',color='blue', label='Validation loss')
plt.title('Training and Validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss function')
plt.legend()

plt.show()

また、ベースラインを設定しモデルの優位性を証明します。

mae_loss.py

#時系列内で最後の一つ前から最後のデータの加速度が一定であると想定したときの平均絶対誤差(mae)を計算する
#ただしデータ取得の間隔が一定であると仮定する

batch_maes = []
for i in range(len(X_test)//batch_size):
    preds = X_test[i*batch_size:(i+1)*batch_size,-1,-1]*2 -X_test[i*batch_size:(i+1)*batch_size,-2,-1]
    terget = t_test[i*batch_size:(i+1)*batch_size,-1]
    mae = np.mean(np.abs(preds-terget))
    batch_maes.append(mae)

standard_mae = np.mean(batch_maes)
print("平均絶対誤差（正規化）：" + str(standard_mae)) 
#平均絶対誤差（正規化）：0.0009700724
print("平均絶対誤差 （km/h） ：" + str(standard_mae * Xt_max)) 
#平均絶対誤差 （km/h） ：11.100591540619897

計算したベースラインの平均絶対誤差は0.0010となり、参考のブログ結果（0.0837）に比べかなり小さい結果となりました。
一方、モデルの損失関数は0.0008に収束しており、こちらも参考ブログ（0.0461）に比べ小さい結果でした。参考ブログと同様の処理をしているため同等となると予測しておりましたが、実際は小さくなっており原因も掴めずですが、損失関数が小さい側であるため、このまま進めることとします。

次にプロット用のデータをモデルに読み込み、予測値から各地点の誤差を取得したいと思います。
その後、データを正常データと異常データに分けます。

python.split_data.py

X_plot = X_plot.astype(np.float32)
plot_predict = model.predict(X_plot, batch_size=1)

#予測した値とy_plotとの絶対誤差を計算する
plot_predict_mae=np.abs(plot_predict[:,0]-t_plot[:,-1])

#gps_correct_dataからプロット用のデータを作成
gps_plot_data = gps_correct_data[data_index[(-plot_data_number):],:]
plot_data = np.concatenate([gps_plot_data,plot_predict_mae.reshape(len(plot_predict_mae),1)], axis=1)
plot_data=plot_data[:,(0,2,3,7)]

#plot用の絶対誤差と常識的な基準として作成した平均絶対誤差を比較する
#plot用の絶対誤差 < 常識的な平均絶対誤差 となるデータを正常とする
#plot用の絶対誤差 > 常識的な平均絶対誤差 となるデータを異常とする
clustering_normaly_gps = X_plot[np.where(plot_data[:,-1]<standard_mae)[0],:,-1]
clustering_anormaly_gps = X_plot[np.where(plot_data[:,-1]>standard_mae)[0],:,-1]

④tslearnを用いた時系列データのクラスタリング

では、小さいデータ（正常データ）、誤差が大きいデータ（異常データ）それぞれに対してクラスタリングをしていきます。
距離関数は参考ブログと同じくユークリッド距離を用います。

クラスタリングのクラスター数を確からしさを求めるために、シルエット値を利用します。
シルエット値とはクラスタリングが正しくできているかの指標です。
シルエット値は0から1の値を取り、１に近づけば同一クラスター内の距離がそれだけ近くなります。
クラスター数が2から50までのシルエット値を取得します。

clustering.py

#tslearnをインストールする（参考ブログには記載ないため追加） 
!pip install tslearn

from tslearn.clustering import TimeSeriesKMeans
from sklearn.metrics import silhouette_samples, silhouette_score

#クラスタリングに用いるデータ数
clustering_data_number = 10000

#データ分割用のインデックスの準備
np.random.seed(0)
normaly_data_number = len(clustering_normaly_gps)
normaly_data_index = np.arange(normaly_data_number)
np.random.shuffle(normaly_data_index)
anormaly_data_number = len(clustering_anormaly_gps)
anormaly_data_index = np.arange(anormaly_data_number)
np.random.shuffle(anormaly_data_index)

#時速データの準備
normaly_ts_dataset = clustering_normaly_gps[normaly_data_index[:clustering_data_number],:]
anormaly_ts_dataset = clustering_anormaly_gps[anormaly_data_index[:clustering_data_number],:]

#データの保存
silhouette_normaly_data = []
km_normaly_labels = []
km_normaly_center = []
silhouette_anormaly_data = []
km_anormaly_labels = []
km_anormaly_center = []

#クラスタリングの実行
metric = 'euclidean'
n_clusters = [n for n in range(2, 50)]

print("正常値のクラスタリング")
for n in n_clusters: 
    km= TimeSeriesKMeans(n_clusters=n, metric=metric, verbose=False, random_state=1).fit(normaly_ts_dataset)
    print('クラスター数 ='+ str(n) + 'シルエット値 ='+ str(silhouette_score(normaly_ts_dataset, km.labels_, metric=metric)))
    silhouette_normaly_data.append(np.array([n, silhouette_score(normaly_ts_dataset, km.labels_, metric=metric)]))
    km_normaly_labels.append([n, km.labels_])
    km_normaly_center.append([n, km.cluster_centers_])

print("異常値のクラスタリング")
for n in n_clusters: 
    km= TimeSeriesKMeans(n_clusters=n, metric=metric, verbose=False, random_state=1).fit(anormaly_ts_dataset)
    print('クラスター数 ='+ str(n) + 'シルエット値 ='+ str(silhouette_score(anormaly_ts_dataset, km.labels_, metric=metric)))
    silhouette_anormaly_data.append(np.array([n, silhouette_score(anormaly_ts_dataset, km.labels_, metric=metric)]))
    km_anormaly_labels.append([n, km.labels_])
    km_anormaly_center.append([n, km.cluster_centers_])

結果は以下のようになります。

参考ブログとは若干値が違うが、正常・異常データともにクラスター数が2の時シルエット値が最大になり、徐々に減少していく傾向は同じとなり、おおよそ再現はできていると判断した。

異常データのシルエット値が正常データに比べ低い関係も再現できています。
この結果から、モデルの再現はできたと判断しました。

⑤kepler.glを用いたデータの可視化

それではデータの可視化を行います。
渋滞のデータを時間毎にプロットしたものが下になります。

参考ブログのように渋滞の入り口と出口を以下のように表しました。
・薄い水色のデータ：正常の渋滞データ
・黄色のデータ：正常の渋滞入口データ
・緑色のデータ：正常の渋滞出口データ

渋滞発生箇所を確認でき、参考ブログの再現ができたと判断しました。

2.データの緯度経度の範囲内にあるバス停の緯度経度情報をGoogle MAPから抽出

次に今回のデータセットからバス停の位置に重なるデータを確認します。
バス停位置は渋滞で渋滞ではなく停止している可能性があるため、取り除くことで精度の向上が見込めます。

まず、今回のデータセットの範囲にあるバス停の位置を調べるためGoogle MAP APIというプログラムを使用します。
公式HP：https://developers.google.com/maps/?hl=ja

まずはプログラムをインストールします。

install.py

#Google Maps APIからプログラムをインストールする 
!pip install pygeocoder
!pip install googlemaps

次にモジュールをインストールします。

module_inport.py

# モジュールのインポート
import pandas as pd
import urllib
import urllib.error
import urllib.request

# Google API モジュール
from pygeocoder import Geocoder
import googlemaps

#アカウントを作成しキーを取得、入力する。
key = '#キーを入れる'
client = googlemaps.Client(key)

インストールが完了したら、データセットを改めて取り込み、
データの範囲を確認します。
データの範囲は緯度経度の最大値、最小値を抽出し範囲を把握します。

read.py

#データセットを読み出す
import pandas as pd
df = pd.read_csv('/content/drive/MyDrive/transjakarta_gps.csv')

#データセットの緯度と経度の最大最小値を取得する
min_max = [df['latitude'].min(), df['latitude'].max(),df['longitude'].min(),df['longitude'].max()]
print(min_max)

#最大値と最小値から中心点を算出する
center_lat = (min_max[0]+min_max[1])/2
center_long = (min_max[2]+min_max[3])/2
print(center_long, center_lat)

#最大値と最小値からデータエリアの大きさを確認する
center_lat_dis = (min_max[0]-min_max[1])/2
center_long_dis = (min_max[2]-min_max[3])/2
print(max(abs(center_long_dis), abs(center_lat_dis))*111000)

確認の結果、データセットの範囲は緯度経度で以下の範囲でした。
緯度：-6.791528 〜 -6.048802
経度：106.607 〜 108.330973

この範囲を確認したところ、ジャカルタ市街地だけでなく東側の郊外なども含まれていることが分かりました。
今回は渋滞が発生している市街地に絞ることとし、マップからジャカルタの市街地の中央と思われる緯度経度を確認。
市街地が縦横50km程度の範囲にあるため、この範囲でバス停を抽出することにしました。
Google MAP APIを使ってバス停検索を実施します。

data_extraction.py

#バス停の検索を定義
def get_busstop(next_page_token=None):
  get_result = result2 = client.places_nearby((-6.181629201591928, 106.83646409440748),radius=50000,page_token=next_page_token,type='transit_station',language='ja')
  return get_result

#サーバーアクセスの間隔を定義し確実に取得できるようにする
import time
next_page_token = None
tmp_dic = {'name':[], 'lat':[], 'lng':[]}
while True:
  results = get_busstop(next_page_token)

  
  for result in results['results']:
    tmp_dic['name'].append(result['name'])
    tmp_dic['lat'].append(result['geometry']['location']['lat'])
    tmp_dic['lng'].append(result['geometry']['location']['lng'])
  if 'next_page_token' in list(results.keys()):
    next_page_token = results['next_page_token']
    time.sleep(5)
  else:
    break

#データ出力
pd.DataFrame(tmp_dic).drop_duplicates()

検索の結果、データのエリア内から59個のバス停が抽出された。

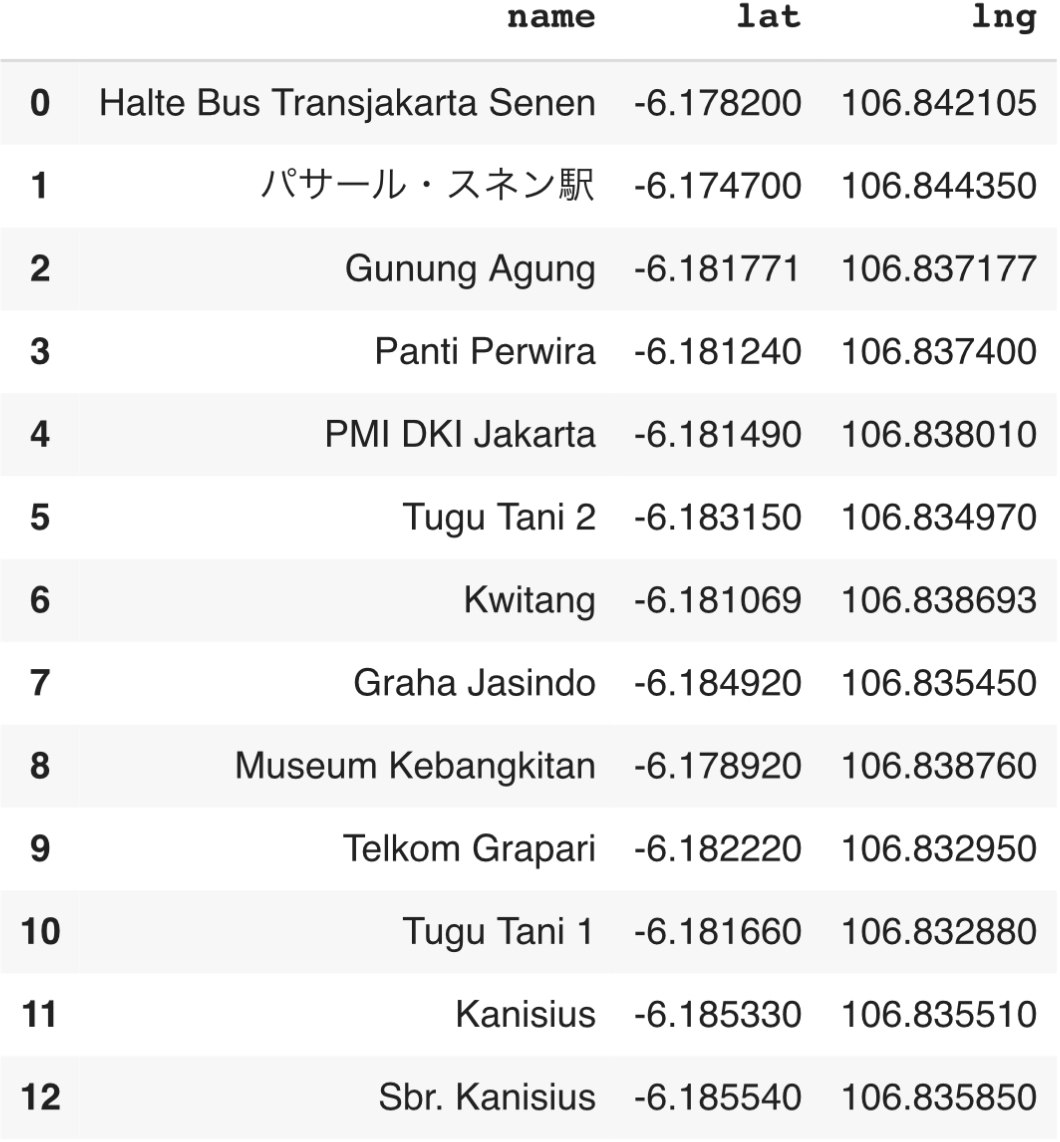
ただ、今回の検出は“transit_station”で抽出したため、バス停以外に駅も含まれている可能性があります。
名前からは判断できないこと、マップと照らし合わせた結果おおよそバス停と一致しているためこの結果を使用することとしました。

3.バス停の位置に付近のデータを除外して再度学習し、モデル精度や渋滞発生位置の変化について考察を実施

では、2.で抽出した各バス停位置の情報を用いて、データセットからバス停付近のデータを除外する。

今回は感覚的にバス停の周囲20mの範囲を対象にすることした。
20mの範囲を緯度経度に置き換える場合、その場所の緯度経度によって距離と方位角の関係は変化する。
ジャカルタで方位角1°あたり106kmであるため、20mでは0.00019°となる。
抽出したバス停位置から半径20mの範囲に該当するデータを以下で抽出する。

remove_data.py

import pandas as pd
#locate_df = pd.read_csv('/content/drive/MyDrive/transjakarta_gps.csv')
locate_df = tmp_dic

locate_df = locate_df[['lat', 'lng']]
diff = 0.00019
locate_df['lat_minus'] = locate_df['lat']- diff
locate_df['lat_plus'] = locate_df['lat']+ diff
locate_df['lng_minus'] = locate_df['lng']- diff
locate_df['lng_plus'] = locate_df['lng']+ diff
# bus_stop_flgでバス停かどうかを判定する
gps_data['bus_stop_flg1'] = 0
gps_data['bus_stop_flg2'] = 0
gps_data['bus_stop_flg3'] = 0
gps_data['bus_stop_flg4'] = 0
for i in range(len(locate_df)):
    lat_minus = locate_df.loc[i, 'lat_minus']
    lat_plus = locate_df.loc[i, 'lat_plus']
    lng_minus = locate_df.loc[i, 'lng_minus']
    lng_plus = locate_df.loc[i, 'lng_plus']
    gps_data['bus_stop_flg1'] = gps_data['latitude']>=lat_minus
    gps_data['bus_stop_flg2'] = gps_data['latitude']<=lat_plus
    gps_data['bus_stop_flg3'] = gps_data['longitude']>=lng_minus
    gps_data['bus_stop_flg4'] = gps_data['longitude']<=lng_plus
gps_data.loc[gps_data[gps_data.columns[-4:]].sum(axis=1)==4,'bus_stop_flg']=1
gps_data[gps_data["bus_stop_flg"]==1]

この検索条件から上記の31件のデータが抽出されました。
データセットは70万件以上のデータが含まれているにも関わらず、
わずか31件のデータのみとなっており、且つ全て同じ号車のデータでした。

それでもデータを除去し精度向上を図れる可能性があるか確認を試みましたが、
今回抽出されたデータは全てテストデータに含まれており、訓練データには含まれていないため精度向上にはならないと判断しました。

今回原因としては、バス停の抽出数の少なさが挙げられます。
ジャカルタ市街地の50km四方で検出したにも関わらず、実際に抽出されたバス停はわずか約2km四方の範囲（以下マップの赤線四角）のものでした。

これはGoogle MAP APIの抽出の仕組みが影響しているようです。
バス停抽出時の中心の緯度経度を変更し同じく50km四方で抽出した結果、
やはり2km程度の小さい範囲のバス停が抽出されました。
ただし抽出されたバス停は変わっているため、中心位置を変更しながら格子状に
抽出していく必要があるようです。

今回は時間の制約でここまでとなりますが、今後の課題としてトライしてみようと思います。

結果

バスの走行データから渋滞予測をするブログの精度向上を狙い以下の結果となりました。

①参考としたブログの再現はできました。
　再現するにあたりブログに記載のコードでは再現できない箇所複数ありコードの修正を実施しました。

②バス停の抽出をGoogle MAP APIで実施し、マップからバス停の抽出を行うことはできました。
　ただし、抽出の条件の作り込みが不十分でモデルの精度向上までは至りませんでした。

反省点・今後の課題

今回の反省点として以下が挙げられます。

計画の甘さ
　今回は学習のまとめとして課題を決め取り組みましたが、
　どの程度の時間が各工程にかかるかの見積もりが甘かったため、
　モデルの精度向上に至りませんでした。
　今後は余裕を持った計画で進める必要があると感じました。

目的の明確化
　参考にしたブログでバス停の考慮ができていないという記載を見て、
　安直に作成を開始してしまいましたが、そもそもGPSの精度がどの程度か、
　それによってバス停位置がわかっても十分に精度向上するのか、
　など事前検討が必要でした。

Google MAP APIについての知識不足
　今回バス停の抽出に用いたGoogle MAP APIについて、
　どのような条件で抽出しているかの下調べが不十分であったため、
　実行後に狙い通りできていないことが分かりました。
　用いるアプリケーションの事前の確認を行う必要があると感じました。

ここまで、ご覧いただきありがとうございました。
自分で触ってみてわかることが多く、実際に自分で何かを作成してみることが一番の学びになると感じました。
引き続き学びを深めていきたいと思います。