はじめに
こんにちは。Qiita初登校・エンジニア転職を目指し勉強中のものです。
プログラミングに初めて触れた、深層学習の勉強をまともに始めたのが今年の一月というかなりの初心者でございます。
学習のアウトプット発信の一環として本記事を発信させていただきます。
至らぬ点等ございますでしょうが、どうか暖かくご指摘・コメントを頂ければ幸いです。
環境
・Windows 10 Home 1909
・anaconda 2020.02
・python 3.7.6
・keras 2.3.1
・tslearn 0.4.1
目的
本記事では、GPSと取得時間のデータを用いて、道路状況を解析・予測をすることを目的とします。
解析・予測する道路状態は、「渋滞」についてです。
実施手順
1、リカレントネットワークを用いてGPS情報から次の時間の時速を予測するモデルを作成する。
作成したモデルから得られた予測値と実測値を比較し、誤差の大きい箇所を異常データ、小さい箇所を通常データとする。
2、tslearnを用いて時系列データのクラスタリングをする。
通常データと異常データそれぞれに対しクラスタリングを行い、分析・要因調査を行う。
3、kapler.glを用いて結果の可視化を行う。
※tslearnとはk-means法を用いて時系列クラスタリングをすることを目的としたpythonパッケージのこと
参考:https://irukanobox.blogspot.com/2019/05/python.html?m=0
※kapler.glとはコードを全く使わずに位置情報データを可視化することができるウェブサービスのこと
参考:https://note.com/kazukio/n/n3407e34d2985
それでは以下より、実施手順の詳細に入りたいと思います。
1. データの確認・前処理
今回はkaggle内にあるデータセット:Transjakarta Bus GPS Data( https://www.kaggle.com/rasyidstat/transjakarta-bus-gps-data )を用いて学習を行います。
2019年11月26日の14時から18時の間に走行したバスのGPSを30秒毎に取得したデータのようです。
なにはともあれ、データの中身を確認していきます。
gps_data = pd.read_csv('transjakarta_gps.csv')
gps_data.head()
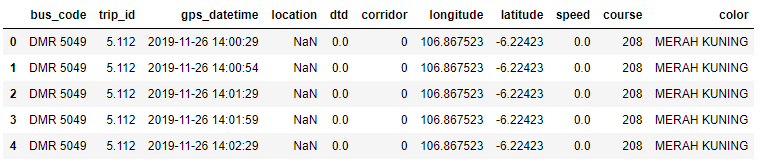
bus_codeやtrip_idなどの位置情報に関係がなさそうな情報が多く含まれています。
他の情報はさておき、bus_codeとtrip_idが変化したタイミングではデータの連続性が危ぶまれそうです。
次に欠損値の確認を行います
print(len(gps_data))
print(gps_data.isnull().sum())
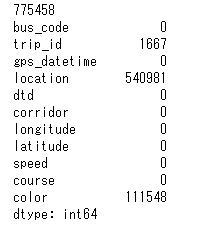
経度と緯度の情報がしっかり入っているため特に問題はなさそうです。
以下、numpy配列にし、時間変化・変位・時速の情報を追加していきます。
# np.arrayの配列を作成
bus_trip_gps = gps_data[["bus_code", "trip_id","gps_datetime", "longitude", "latitude"]]
bus_gps = bus_trip_gps.values
# 距離の変位を調査する
bus_gps_plus = np.vstack((np.zeros(2).reshape(1,2), bus_gps[:, 3:5]))
bus_gps_minus = np.vstack((bus_gps[:, 3:5], np.zeros(2).reshape(1,2)))
delta_bus_gps = bus_gps_plus - bus_gps_minus
delta_bus_gps = delta_bus_gps[1:,:]
# 直感的に異常値に気付けるように単位をkmにする
delta_bus_gps*=110.94297
# 距離のデータを作成
delta_distans = (np.square(delta_bus_gps[:,0:1]) + np.square(delta_bus_gps[:, 1:2]))**0.5
# 時間の変化のデータを作成
bus_time_minus = pd.to_datetime(bus_gps[:-1,2:3].reshape(-1))
bus_time_plus = pd.to_datetime(bus_gps[1:,2:3].reshape(-1))
delta_time_gps = bus_time_plus - bus_time_minus
delta_time_gps = delta_time_gps/np.timedelta64(1,'s')
delta_time_gps = np.array(delta_time_gps, dtype='float')
delta_time_gps = np.append(delta_time_gps,0)
delta_time_gps = delta_time_gps.reshape(len(delta_time_gps),1)
# 変化量、速度を時速になおす
delta_bus_gps /= (delta_time_gps + 1e-8)/(60*60)
delta_distans /= (delta_time_gps + 1e-8)/(60*60)
# bus_gpsに変位と距離を追加する
bus_gps = np.insert(bus_gps,[5] , delta_bus_gps, axis=1)
bus_gps = np.insert(bus_gps,[7] , delta_distans, axis=1)
bus_gps = np.insert(bus_gps,[3] , delta_time_gps, axis=1)
では、時系列データの作成に取り掛かります。今回は、5つ連続するデータ(約150秒)で一つの時系列データとしました。
また、trip_idとbun_codeの変化が起きたときにデータの連続性が危ぶまれるため、その変化点で違う時系列データとして扱うように処理しています。
# 5回の測定で一回の時系列データとする
# bus_codeとtrip_idで別々の時系列のデータとなるようにする。
gps_input_data=[]
gps_correct_data =[]
len_sequence = 5 # 時系列の長さ
bus_gps[:,0:2] = bus_gps[:,0:2].astype(np.str)
bus_code_list = np.unique(bus_gps[:,0:1])
for i in range(len(bus_code_list)):
bus_code = bus_code_list[i]
bus_code_gps = bus_gps[np.any(bus_gps==bus_code,axis=1)]
trip_id_list =np.unique(bus_code_gps[:,1:2])
if i%100 == 0:
print(i)
for j in range(len(trip_id_list)):
trip_id = trip_id_list[j]
trip_id_gps = bus_code_gps[np.any(bus_code_gps[:,1:2]==str(trip_id),axis=1)]
if len(trip_id_gps)>(len_sequence+2):
for k in range(len(trip_id_gps)-(len_sequence+2)):
gps_input_data.append(trip_id_gps[k:k+len_sequence,2:])
gps_correct_data.append(trip_id_gps[k+len_sequence:k+(len_sequence+1),2:].reshape(7))
# インプット用のデータ
# axis0 データ、axis1 同一データ内の時系列位置 axis2 時間、時間変化、緯度,経度,緯度方向変位(km),経度方向変位(km),時速(km/h)
gps_input_data=np.array(gps_input_data)
# 正解用のデータ
# axis0 データ、axis1 時間、時間変化、緯度,経度,緯度方向変位(km),経度方向変位(km),時速(km/h)
gps_correct_data =np.array(gps_correct_data)
これでモデルにインプットする用のデータ、正解用のデータが作成できました。
2. 異常値の削除
異常値の削除を行っていきます。削除するデータは以下の三つです。
1、時速が150km/hを超えているもの
2、時系列内で移動がほとんどないもの
3、データをおおよそ30秒毎に取得できていないもの
以下実行コードです。
# 異常な値の削除
# 正解の時速が150kmを超えているものを異常とみなす
high_distans_index0 = np.where(gps_input_data[:,:,-1]>150)
high_distans_index0 = high_distans_index0[0]
high_distans_index1 = np.where(gps_correct_data[:,-1]>150)
high_distans_index1 = high_distans_index1[0]
error_data_index=np.concatenate([high_distans_index0, high_distans_index1])
error_data_index=np.unique(error_data_index)
gps_input_data = np.delete(gps_input_data,error_data_index,axis=0)
gps_correct_data = np.delete(gps_correct_data,error_data_index,axis=0)
# データの時系列内での(1個目と5個目)移動距離が0.01km以下のものを異常とする
index_destans0 = np.where(((gps_input_data[:,:,4].sum(axis=1)**2 + gps_input_data[:,:,5].sum(axis=1)**2)**0.5) < 0.01)
index_destans0 = np.array(index_destans0)
index_destans0 = index_destans0.reshape(-1)
gps_input_data = np.delete(gps_input_data,index_destans0,axis=0)
gps_correct_data = np.delete(gps_correct_data,index_destans0,axis=0)
# 時間の変位が25より小さい,35より大きいデータを異常とみなす
index_time_short0 = np.where(gps_input_data[:,:,1]<25)
index_time_short0 = index_time_short0[0]
index_time_short1 = np.where(gps_correct_data[:,1]<25)
index_time_short1 = index_time_short1[0]
index_time_short = np.concatenate([index_time_short0, index_time_short1])
index_time_long0 = np.where(gps_input_data[:,:,1]>35)
index_time_long0 = index_time_long0[0]
index_time_long1 = np.where(gps_correct_data[:,1]>35)
index_time_long1 = index_time_long1[0]
index_time_long = np.concatenate([index_time_long0, index_time_long1])
index_time_error = np.concatenate([index_time_long, index_time_short])
index_time_error = np.unique(index_time_error)
gps_input_data = np.delete(gps_input_data,index_time_error,axis=0)
gps_correct_data = np.delete(gps_correct_data,index_time_error,axis=0)
3. LSTM(keras)を用いた速度の予測モデルの作成
リカレントネットワークの作成に入る前に、データの分割を行います。
以下の三つにデータを分割します。
・学習用:ネットワークの学習に用いる。
・評価用:ネットワークの評価に用いる。過学習していないか、表現力が足りているかどうか等の判断材料にする。
・プロット用:学習後のモデルに対し、誤差を測定するデータに用いる。
各地点毎の標準的な速度をモデルに学習させるために、使用するデータは以下を用いることにしました。
・時間変化
・緯度 / 経度
・緯度経度から求めた速度
# データ分割用のインデックスの準備
np.random.seed(0)
all_data_number = len(gps_correct_data)
data_index =np.arange(all_data_number)
np.random.shuffle(data_index)
# 時速データの準備
X = gps_input_data[:,:,(1,2,3,6)]
t = gps_correct_data[:,(1,2,3,6)]
# 正規化
for i in range(len(t[0,:])):
Xt_min = np.min((X[:,:,i].min(), t[:,i].min()))
Xt_max = np.max((X[:,:,i].max(), t[:,i].max()))
X[:,:,i] = (X[:,:,i]-Xt_min)/Xt_max
t[:,i] = (t[:,i]-Xt_min)/Xt_max
# データの分割
train_data_number =(all_data_number*3)//5
plot_data_number = (all_data_number*1)//5
X_train = X[data_index[:train_data_number],:,:]
t_train = t[data_index[:train_data_number]]
X_test = X[data_index[train_data_number:(-plot_data_number)],:,:]
t_test = t[data_index[train_data_number:(-plot_data_number)]]
X_plot = X[data_index[(-plot_data_number):],:,:]
t_plot = t[data_index[(-plot_data_number):]]
それではモデルの構築に入ります。モデルの構築にはkerasを使用します。
使用するリカレント層はLSTMを使用し、リカレントドロップアウトを使用します。
誤差関数は、単純な回帰ということもあり、今回は直感的に誤差の速度を把握しやすい平均絶対誤差(mae)を使用します。
input_dim = 4 # 入力データの次元数
output_dim = 1 # 出力データの次元数
num_hidden_units_1 = 64 # 隠れ層1のユニット数
num_hidden_units_2 = 32 # 隠れ層2のユニット数
batch_size = 1000 # ミニバッチサイズ
num_of_training_epochs = 200 # 学習エポック数
model = Sequential()
model.add(LSTM(num_hidden_units_1,
input_shape=(len_sequence,input_dim),
return_sequences = True,
recurrent_dropout = 0.5))
model.add(LSTM(num_hidden_units_2,
recurrent_dropout = 0.3))
model.add(Dense(output_dim))
model.compile(loss="mae",
optimizer=RMSprop())
model.summary()
# モデルの学習
history=model.fit(X_train,
t_train[:,-1],
epochs=num_of_training_epochs,
batch_size=batch_size,
validation_data=(X_test,t_test[:,-1]))
# 学習結果の可視化
plt.plot(range(num_of_training_epochs),history.history["loss"], 'bo',color='red', label='Training loss',markersize=3)
plt.plot(range(num_of_training_epochs),history.history["val_loss"], 'b',color='blue', label='Validation loss')
plt.title('Training and Validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss function')
plt.legend()
plt.show()
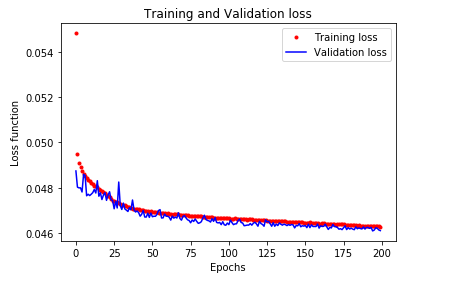
残念ながら結果だけ見ても学習結果が良いかどうか検討もつきません。
そこで仮想的に常識的なベースラインを設定しモデルの優位性を証明することにしました。
# 時系列内で最後の一つ前から最後のデータの加速度が一定であると想定したときの平均絶対誤差(mae)を計算する
# ただしデータ取得の間隔が一定であると仮定する
batch_maes = []
for i in range(len(X_test)//batch_size):
preds = X_test[i*batch_size:(i+1)*batch_size,-1,-1]*2 -X_test[i*batch_size:(i+1)*batch_size,-2,-1]
terget = t_test[i*batch_size:(i+1)*batch_size,-1]
mae = np.mean(np.abs(preds-terget))
batch_maes.append(mae)
standard_mae = np.mean(batch_maes)
print("平均絶対誤差(正規化):" + str(standard_mae)) #平均絶対誤差(正規化):0.083268486903678
print("平均絶対誤差 (km/h) :" + str(standard_mae * Xt_max)) #平均絶対誤差 (km/h) :11.597705343596475
計算した常識的なベースラインの平均絶対誤差は0.0837となりました。
一方、モデルの損失関数の値は0.0461に収束しており、モデルの優位性を証明することができました。
それではプロット用のデータをモデルに読みこみ、予測値から各地点の誤差を取得したいと思います。
その後データを正常データと異常データに分けます。
plot_predict = model.predict(X_plot, batch_size=1)
# 予測した値とy_plotとの絶対誤差を計算する
plot_predict_mae=np.abs(plot_predict[:,0]-t_plot[:,-1])
# plot用の絶対誤差と常識的な基準として作成した平均絶対誤差を比較する
# plot用の絶対誤差 < 常識的な平均絶対誤差 となるデータを正常とする
# plot用の絶対誤差 > 常識的な平均絶対誤差 となるデータを異常とする
clustering_normaly_gps = X_plot[np.where(plot_data[:,-1]<standard_mae)[0],:,-1]
clustering_anormaly_gps = X_plot[np.where(plot_data[:,-1]>standard_mae)[0],:,-1]
4. tslearnを用いた時系列データのクラスタリング
では、小さいデータ(正常データ)、誤差が大きいデータ(異常データ)それぞれに対してクラスタリングをしていきます。
今回使うデータでは時間軸に対してある程度ズレがあっても同じパターンとして認識してくれるように、
距離関数にはDynamic Time Wrapping(DTW)を用いるつもりでした。
しかし、計算コストがあまりに高いためユークリッド距離を用いることにします。
データの時系列が5つしかないため、さして問題はないと判断いたしました。
クラスタリングのクラスター数を確からしさを求めるために、シルエット値を利用します。
シルエット値とはクラスタリングが正しくできているかの指標です。
シルエット値は0から1の値を取り、1に近づけば同一クラスター内の距離がそれだけ近くなります。
クラスター数が2から50までのシルエット値を取得していきます。
# クラスタリングに用いるデータ数
clustering_data_normalnumber = 10000
# データ分割用のインデックスの準備
np.random.seed(0)
normaly_data_number = len(clustering_normaly_gps)
normaly_data_index = np.arange(normaly_data_number)
np.random.shuffle(normaly_data_index)
anormaly_data_number = len(clustering_anormaly_gps)
anormaly_data_index = np.arange(anormaly_data_number)
np.random.shuffle(anormaly_data_index)
# 時速データの準備
normaly_ts_dataset = clustering_normaly_gps[normaly_data_index[:clustering_data_number],:]
anormaly_ts_dataset = clustering_anormaly_gps[anormaly_data_index[:clustering_data_number],:]
# データの保存
silhouette_normaly_data = []
km_normaly_labels = []
km_normaly_center = []
silhouette_anormaly_data = []
km_anormaly_labels = []
km_anormaly_center = []
# クラスタリングの実行
metric = 'euclidean'
n_clusters = [n for n in range(2, 50)]
print("正常値のクラスタリング")
for n in n_clusters:
km= TimeSeriesKMeans(n_clusters=n, metric=metric, verbose=False, random_state=1).fit(normaly_ts_dataset)
print('クラスター数 ='+ str(n) + 'シルエット値 ='+ str(silhouette_score(normaly_ts_dataset, km.labels_, metric=metric)))
silhouette_normaly_data.append(np.array([n, silhouette_score(normaly_ts_dataset, km.labels_, metric=metric)]))
km_normaly_labels.append([n, km.labels_])
km_normaly_center.append([n, km.cluster_centers_])
print("異常値のクラスタリング")
for n in n_clusters:
km= TimeSeriesKMeans(n_clusters=n, metric=metric, verbose=False, random_state=1).fit(anormaly_ts_dataset)
print('クラスター数 ='+ str(n) + 'シルエット値 ='+ str(silhouette_score(anormaly_ts_dataset, km.labels_, metric=metric)))
silhouette_anormaly_data.append(np.array([n, silhouette_score(anormaly_ts_dataset, km.labels_, metric=metric)]))
km_anormaly_labels.append([n, km.labels_])
km_anormaly_center.append([n, km.cluster_centers_])
結果を可視化すると以下のようになりました。
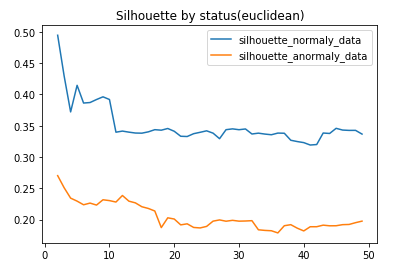
正常・異常データともにクラスター数が2の時シルエット値が最大になり、徐々に減少していきます。
異常データのシルエット値が正常データに比べ低いのは、速度の予測がしづらい=時系列内でデータに整合性がないからでしょうか。
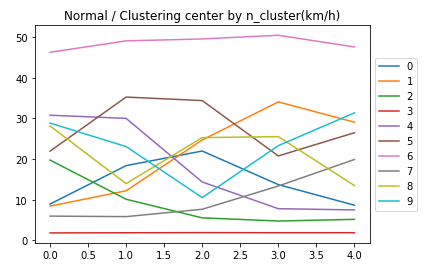
とりあえずクラスター数=2の時のクラスタリングの結果を見てみましょう。
こちらが正常のデータの中心を取ったグラフ(n=2)
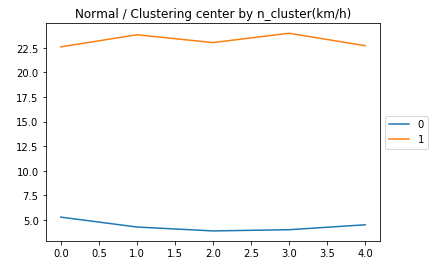
こちらがクラスター毎の実データです(計100個)
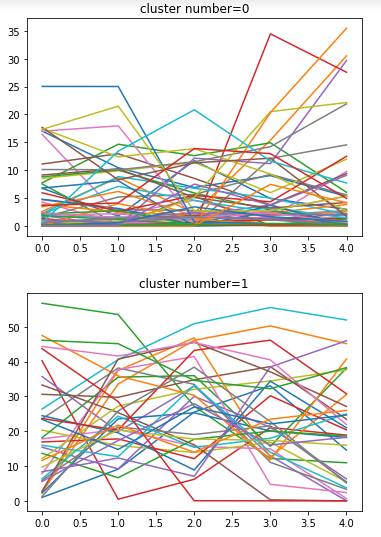
・・・これはクラスタリングできているのでしょうか。
直感的に「渋滞時のデータ」と「正常時のデータ」となればうれしいのですが、そうはならない様子。
ちなみにこちらが異常のデータの中心を取ったグラフ(n=2)
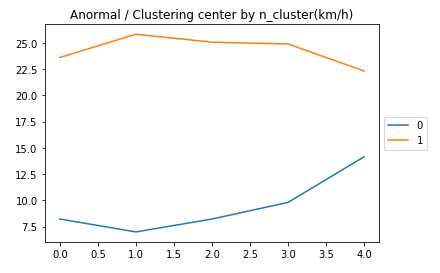
正常のデータと若干波形が違います。これは単なる渋滞の位置ではなく渋滞の終わりの位置とを示しているのかもしれません。
n=2ではシルエット値は最大となるのですが道路状態を分割できるほどクラスタリングしていないため、
それらしくクラスタリングできているnの中で最大となる値を採用することにしました。
正常のデータではn=10、異常のデータではn=12より大きくなる際にシルエット値に解離が大きく見られたためその値を採用します。
n=2 渋滞の入り口
n=3 渋滞
n=7 渋滞の出口
となっているようです。実データを見ても把握することができます。
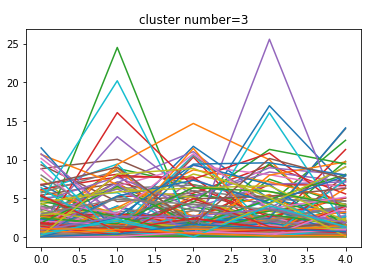
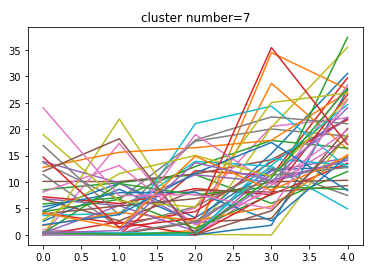
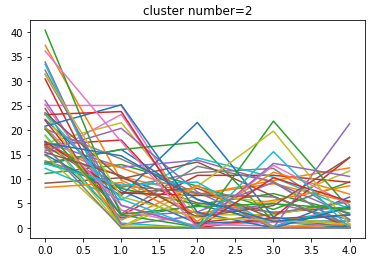
異常データ(n=12)の各データの中心
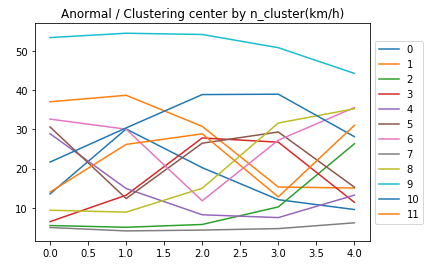
n=2 渋滞の入り口
n=7 渋滞
n=4 渋滞の出口
となっています。
(正常データと同様に実データを見てもそうなっている、今回は割愛)
これらをcsvに出力し、kepler.glに入れれる形にします。
# gps_correct_dataからプロット用のデータを作成
gps_plot_data = gps_correct_data[data_index[(-plot_data_number):],:]
plot_data=np.concatenate([gps_plot_data,plot_predict_mae.reshape(len(plot_predict_mae),1)], axis=1)
plot_data=plot_data[:,(0,2,3,7)]
plot_normaly_gps = plot_data[np.where(plot_data[:,-1]<standard_mae)[0],:]
plot_anormaly_gps = plot_data[np.where(plot_data[:,-1]>standard_mae)[0],:]
# normal用データ作成
n_cluster = 10
lavel = 2
km_labels = km_normaly_labels[n_cluster-2][1]#
normaly_plot_data = plot_normaly_gps[normaly_data_index[:clustering_data_number],:]#
normaly_plot_data_label = normaly_plot_data[np.where(km_labels.reshape(clustering_data_number,1)==lavel)[0],:]#
df_normaly_plot_lavel = pd.DataFrame(normaly_plot_data_label0, columns=['gps_datetime', 'longitude', 'latitude', 'error'])
df_normaly_plot_lavel.to_csv('normaly_plot_lavel='+str(lavel)+'(渋滞の入り口).csv')
5. kepler.glを用いたデータの可視化
それではデータの可視化を行います。
渋滞のデータを時間毎にプロットしたものが下になります。
・水色のデータ:予測に使用した全データ
・黄色のデータ:正常・異常、入口・出口問わずクラスタリングにて渋滞と判断された全データ
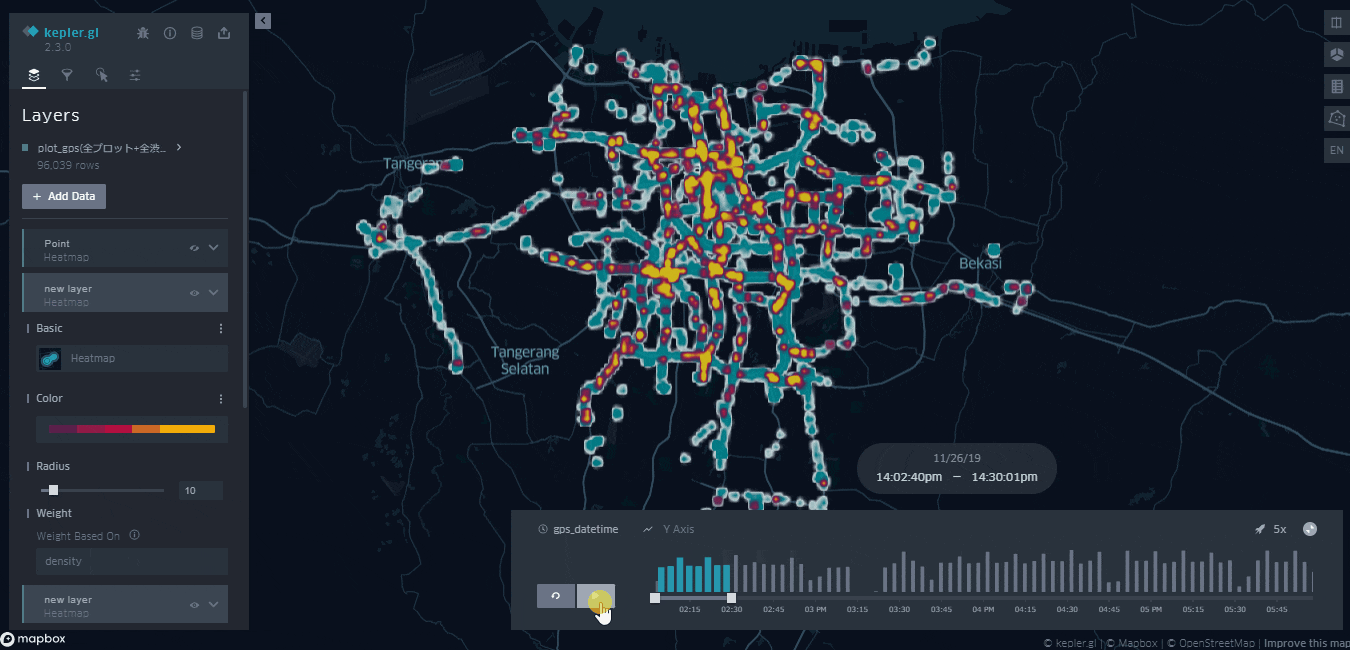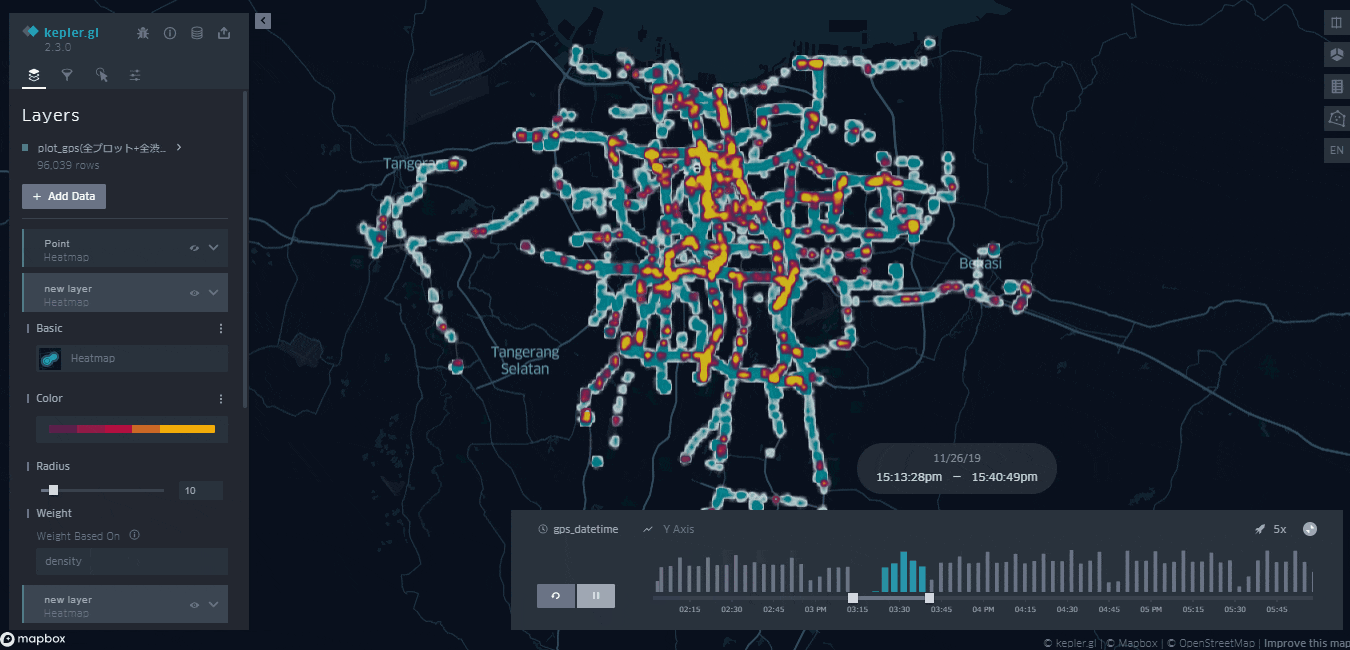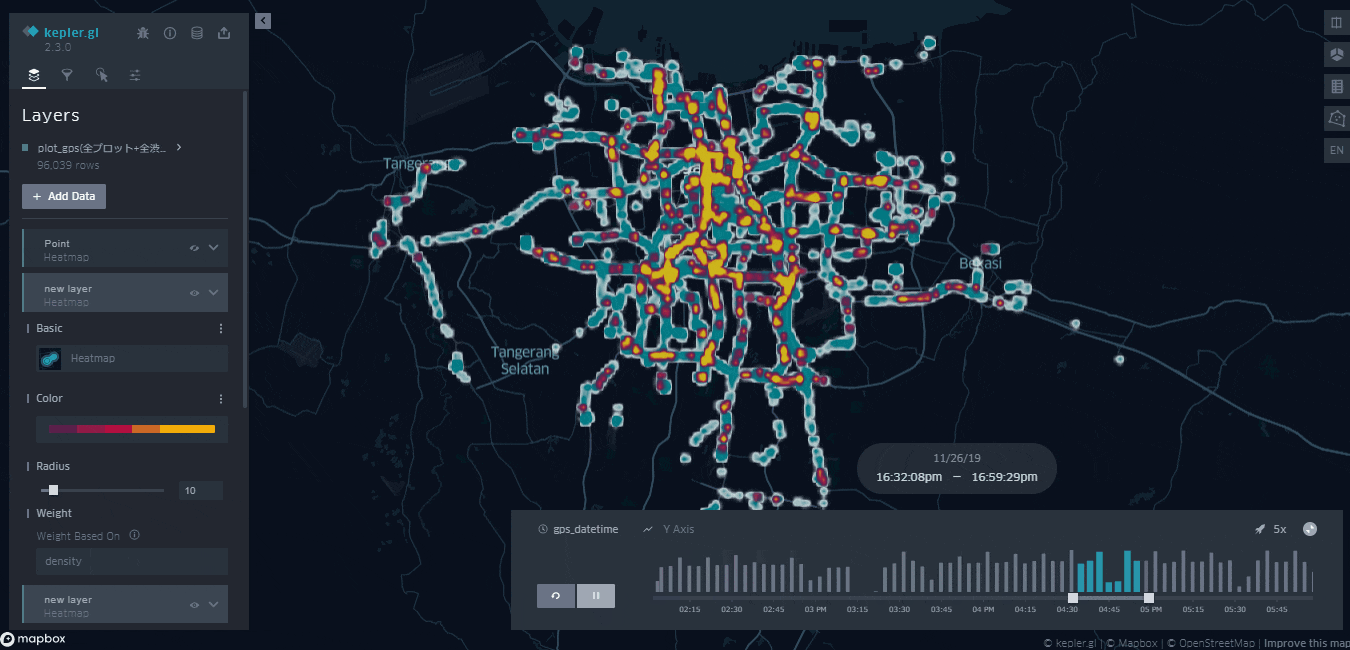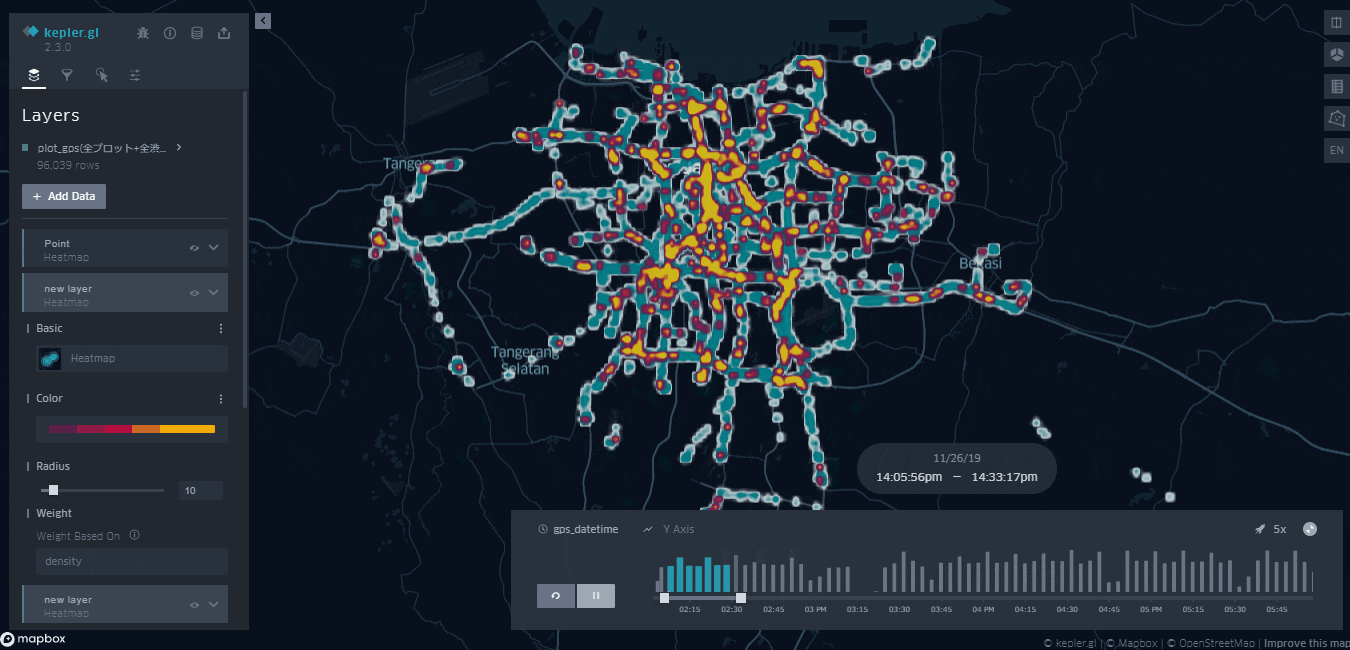
少々荒いですが、時間ごとにどこで渋滞が起きているのかを把握することができます。
予測に使用した全データを同時にプロットすることにより、黄色の面積が少ない箇所は「データの取得率が単純に少ないのでは?」と指摘される心配がなくなります。
これにより、渋滞の度合いをより直感的に把握してもいい画面ということが保証されました。
どうやら都市部を中心に渋滞が起きているようです。一方で都市部から少し離れれば快適な運転が可能なことがうかがえます。
では、渋滞の入り口と出口の違いを見てみましょう。
・薄い水色のデータ:正常・異常の渋滞データ
・黄色のデータ:正常・異常の渋滞入口データ
・緑色のデータ:正常・異常の渋滞出口データ

ぼんやりとデータを眺めていると、はじめは渋滞出口データが多く、渋滞がおだやかに緩和されていることが分かります。
しかし、徐々に渋滞入口データが多くなったと思ったら、あっという間に渋滞の箇所がとても多くなってしまいました。
このことから、渋滞入口データと渋滞出口データは大きな範囲での道路状態を予測するのに役立つ情報になる可能性が分かります。
渋滞のまわりに渋滞の入口が発生するのではなく、渋滞の入口があつまっていつのまにか渋滞が発生しているようなので、
渋滞入口・出口の情報のみでは、ピンポイントでこの場所が渋滞になる、という予測は難しそうです。
最後に正常・異常データの比較を行いましょう。
プロットデータ:正常・異常の渋滞・渋滞入口・渋滞出口のデータ
縦軸・色:モデルでの予測値との誤差

一方こちらは渋滞とそうでないところの境い目で誤差が大きくなっているようです。
誤差が大きくなっている境界で、いつも間にか渋滞に発生したり渋滞が緩和されたりしています。
この情報を用いれば次に渋滞の発生・緩和される個所の場所をある程度絞ることができそうです。
結果
速度予測のモデルとクラスタリングを用いいることによって以下のことを把握できました。
現状:渋滞の位置
予測:今後渋滞が緩和されるか、渋滞が発生するか。どの場所でそれが起こりうるか
今後の課題・反省点
全体の進め方の反省
データ分析をする際に目的が不明確なまま開始してしまった。
特に、速度予測モデルに関しては「こんなことできたら面白いな」という興味本位で取り組んでしまった。
データの選択について
結果的に渋滞を予測することとなったが、今回のデータではバス停で止まっているのか渋滞で遅延しておるのか判断をすることができない。
また、予測した速度もおそらく実際の速度とは解離があり、もっとデータ取得間隔の短いデータを用いるか、
地図と位置をリンクさせ、経路を予想したうえで速度を予測するべきであった。
モデルについて
学習・予測の際にデータ取得位置の情報も入れるべきかの判断を正しく行えなかった。
位置を入れることで地点毎に道路状態を学習させるというと聞こえはいいが、
誤差が高くなってほしい箇所(渋滞の境い目など)を学習し、誤差が不必要に低くなるリスクがあることを考慮できなかった。
クラスタリングについて
結果的にユークリッド距離を使用したため、わざわざ tslearn を使用した意味がなくなってしまった。
また、正常データ・異常データ別々にクラスタリングしたが、今回の解析ではプロットデータのクラスタリングを行うのみで十分であった。
ここまでご覧くださりありがとうございました。
まだまだ学ぶことが多いことを改めて思い知らされました。
これからも日々勉強を続けていきたいと思います。
以上。