はじめに
研究用の脳波解析ツールと言えばMatlabのEEGLABが有名ですが、私はPythonが好みです。というわけでPythonで利用できる脳波解析用のライブラリを探し、MNE-Pythonに行き着きました。
このライブラリは脳波データに使われる様々なフォーマットに対応し、頻繁に利用する処理を簡単に適用できます。加えて、Numpy等の配列に変換しNumpy, Scipyなどのメソッドを適用できます。
そんな便利なMNE-Pythonなのですが、2024年現在日本語の解説記事は多くない印象です。一応全くないわけではなく、MNE-Pythonのチュートリアルを日本語解説記事をsentencebirdさんが投稿されています。しかし、ネットで検索しても3,4つ程度しか見つかりません
そもそも、MNE-Pythonは公式サイトに豊富なチュートリアルが用意されているためユーザーの方で解説記事を書く人が少ないのかもしれません。
しかし、個人的にMNE-Pythonを学び始めたとき、チュートリアルが膨大すぎて手の付け所に戸惑ったこと, チュートリアルの方で触れられていない沼ポイントがあったこと, なんだかんだ日本語の解説記事があると嬉しいと思ったこと, などの理由から本記事を執筆するに至りました。
差別点としては
・データセットはMNE-Pythonからはインポートせず、ネットからダウンロードして使用
・MNE-Pythonのメソッド以外にもNumpyやScipyなどの科学計算ライブラリを用いて解析
・運動想起をテーマとして解説
していることが挙げられます。
本記事ではまず運動想起時の脳波の特徴を紹介します。続いて脳波データセットをダウンロードし、実際にその特徴を抽出し可視化するまでのプログラムを紹介します。
準備
運動想起時の脳波の特徴
本記事で扱う運動想起とは、左手または右手を実際には動かさずに動かすよう想像することを指します。想像するだけでも実際に動かしたときと類似の脳反応を得られることが、意思の力でコンピュータを操作するブレイン・コンピュータ・インターフェースを実現するのための強い手がかりになっています。
運動想起時の脳波の特徴は、事象関連電位(ERP:Event-Related Potential)のようなスパイクというより、α帯域(8~13Hz)やβ帯域(13~Hz)のパワーの増減であると言われます。興味深いのは、動きを想起した腕の反対側でより大きくパワーが減少することです。
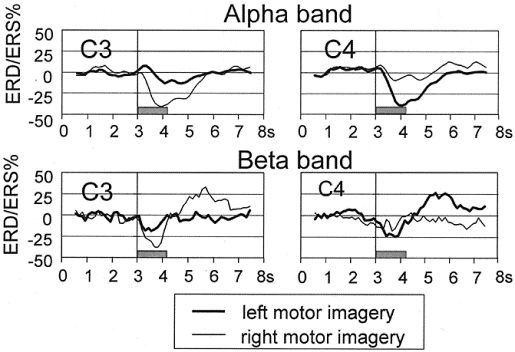
※画像元:G. Pfurtscheller and C. Neuper, "Motor imagery and direct brain-computer communication", in Proceedings of the IEEE, vol. 89, no. 7, pp. 1123-1134, July 2001
データセットの用意
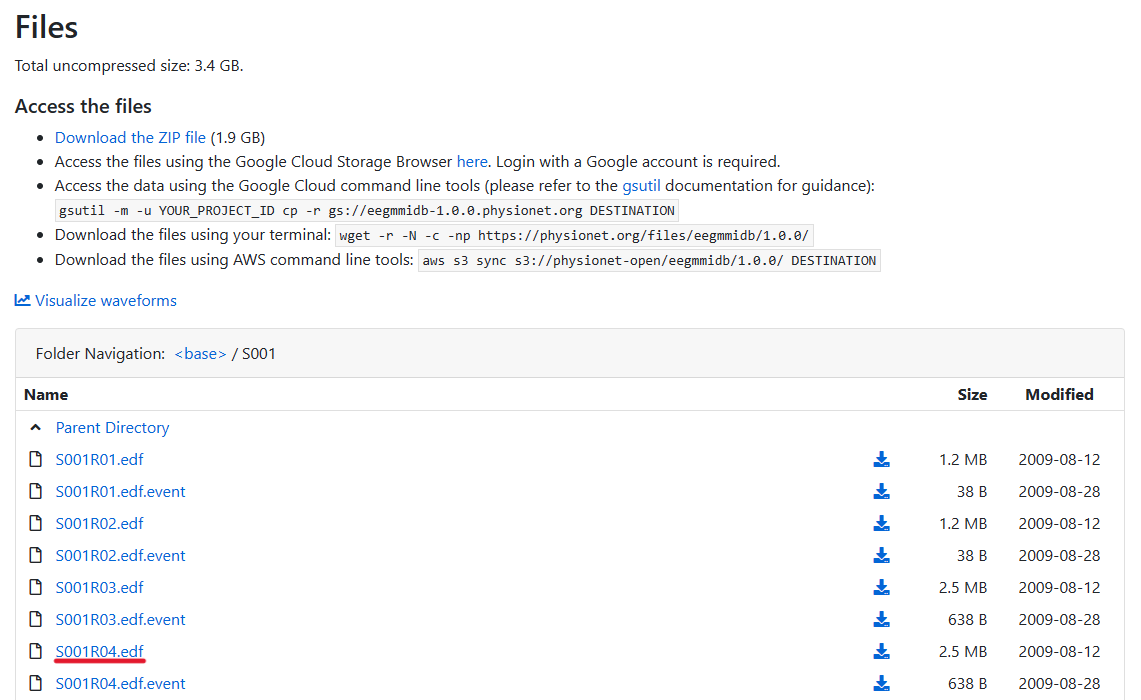
PhysioNetのEEG Motor Movement/Imagery Datasetを使用します。
このデータセットは、109人の被験者に対し64チャンネルの脳波計を用いて、右手/左手, 両手/両足の運動を、実際に行ったとき/想起したときで脳波を計測したものです
本記事ではひとまず1人の被験者の右手/左手の運動を想起したときのデータを解析します。S001フォルダ内のS001R004.edfをダウンロードし、プログラムを動かすpythonファイルと同階層のフォルダに設置してください.
edfファイル:生体信号データのフォーマット
信号に加え計測電極, サンプリングレート, タスク実行時間など、解析に必要な様々な情報を内包したデータ (類似のフォーマットに.gdfというものもある)
解析
データの読み込み
まず始めに、脳波信号をMNE-Python上のrawオブジェクトとしてファイルからデータを読み込みます
import mne
import numpy as np
import matplotlib.pyplot as plt
raw = mne.io.read_raw_edf('S001R04.edf', preload=True)
参考:Importing data from EEG devices
ちなみに、データの読み込みはBrainVisionやBioSemiなど一部のデバイス固有の形式や、EEGLABファイルにも対応しています. 詳細は公式のページを参照してください.
raw信号のプロット
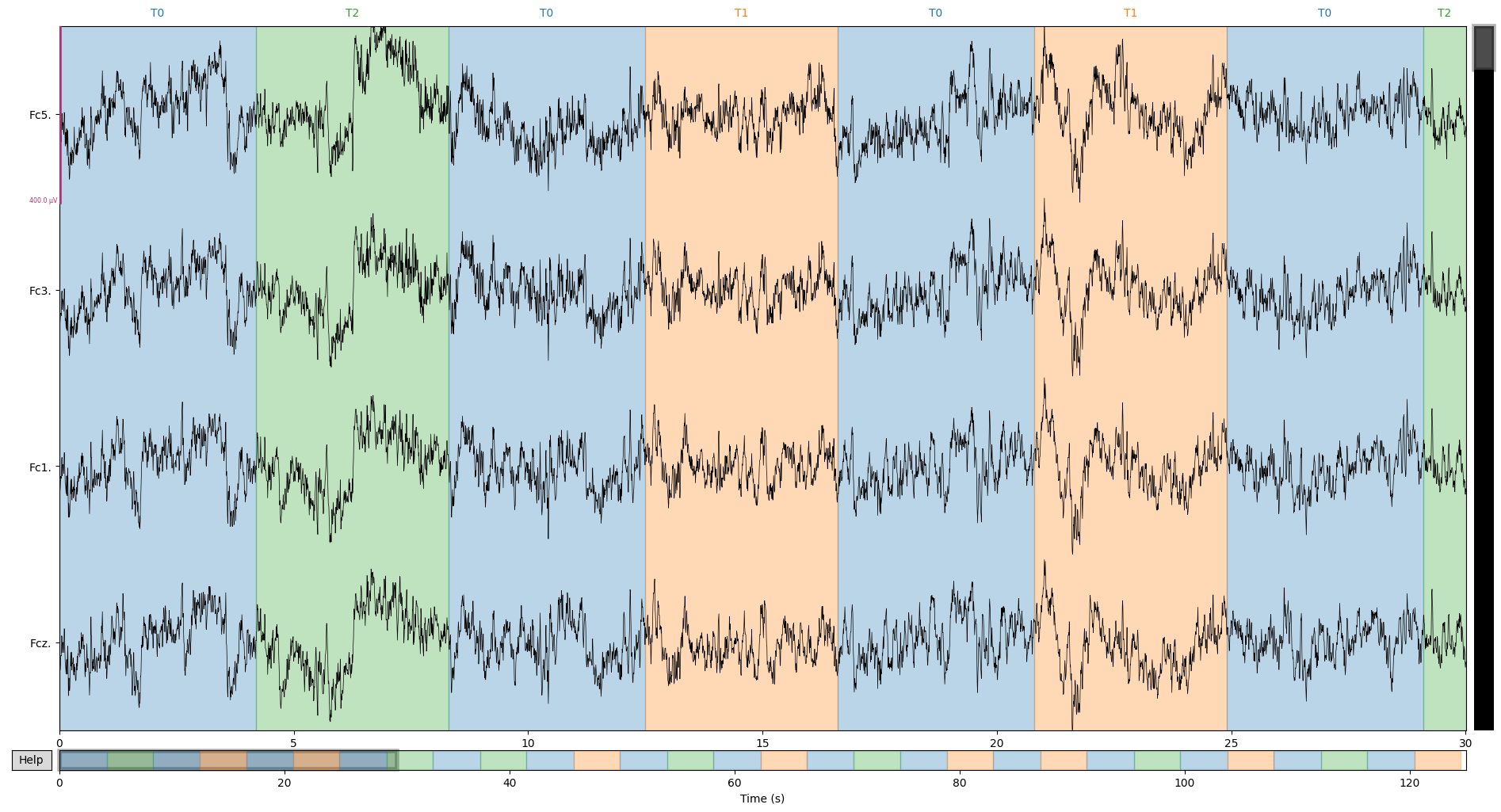
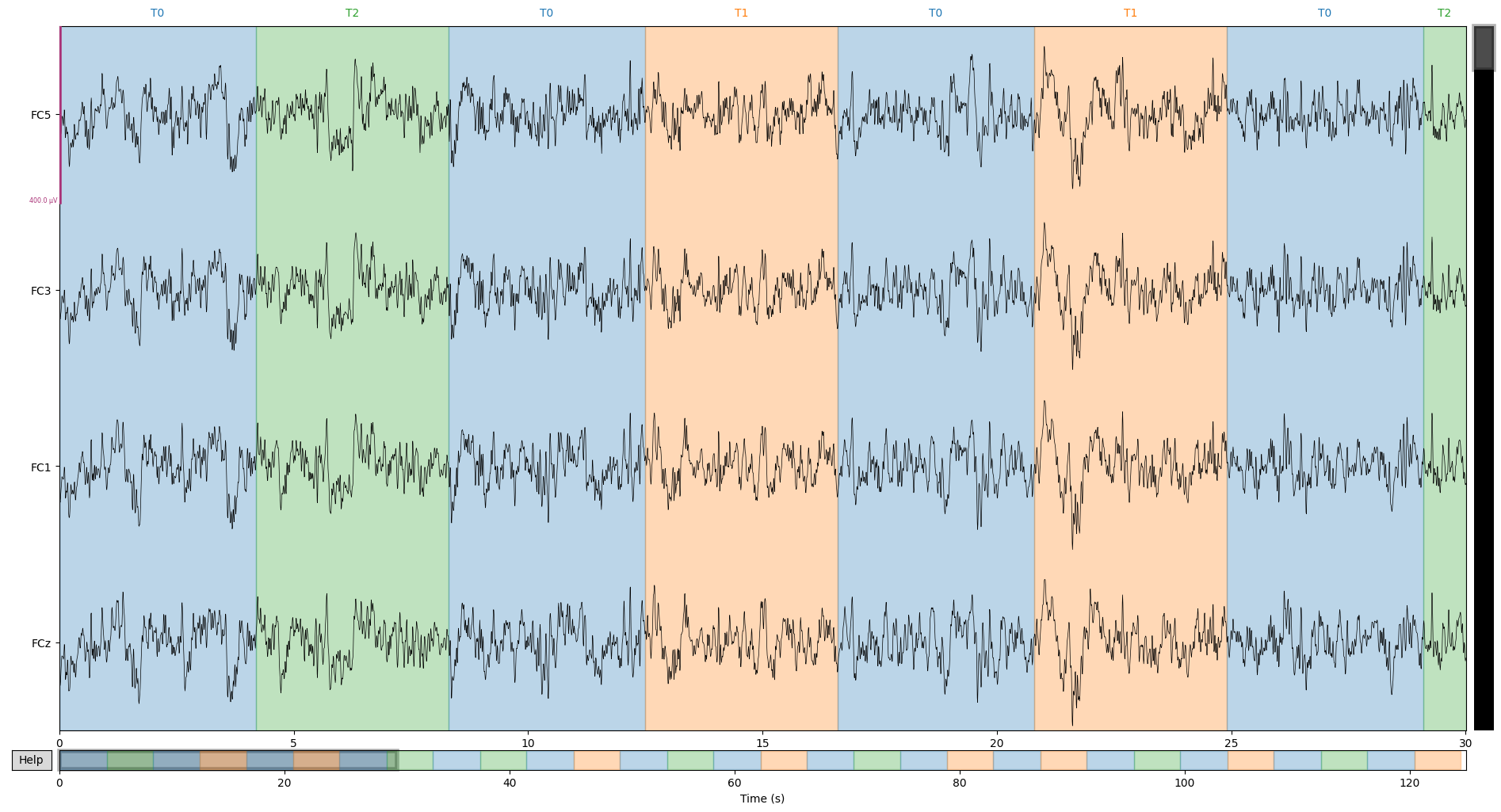
rawオブジェクトを読み込めたら, 計測されたデータをプロットしてみましょう.
raw.plot(duration=30, n_channels=4, scalings={'eeg': 200e-6})
plt.show()
duration:表示する時間の長さ(s)
n_channels:ウィンドウの中に表示するチャンネルの数
scalings:表示する振幅の範囲
※ウィンドウをクリックした状態で+/-入力をすることでインタラクティブに変更できます
各電極の信号に加え, 実験中のタスクなどのイベント情報が表示されます.
パワースペクトル密度
信号の特徴を可視化する方法の1つにパワースペクトル密度(PSD)の算出とプロットがあります。どの周波数がどのくらいのパワーで含まれているかを可視化することで、信号の成分を分かりやすくできます。
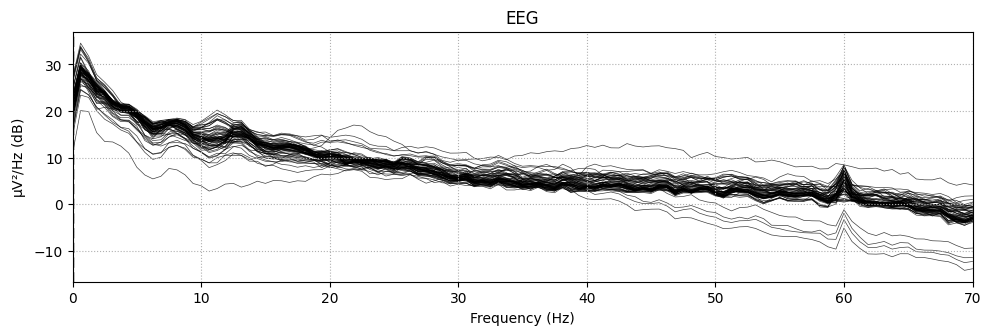
raw.compute_psd(fmin=0,fmax=60).plot()
plt.show(
fmin, fmax:表示する周波数の範囲
それぞれのチャンネルについて、周波数ごとのパワーが表示されます。特に商用交流由来のハムノイズの影響で60Hz付近が山になっている様子が分かります。
電極の名称変更と配置の設定
rawオブジェクトには信号を測定した電極の情報が反映されます。
国際10-20法を始め電極の名前と設置箇所は規定されているため, 本来電極の名前と位置情報はセットで扱うことができます. しかし, 表記が計測ソフトによって若干異なる場合があるためか, MNE-Pythonはrawオブジェクトを読み込んだだけでは電極の位置情報までは反映されません.
そこで, 電極の名前を規定のものに変更し、設置箇所を設定する方法を紹介します.
まず, rawデータの電極名一覧を確認しましょう.
print(raw.ch_names)
---output---
['Fc5.', 'Fc3.', 'Fc1.', 'Fcz.', 'Fc2.', 'Fc4.', 'Fc6.', 'C5..', 'C3..', 'C1..', 'Cz..', 'C2..', 'C4..', 'C6..', 'Cp5.', 'Cp3.', 'Cp1.', 'Cpz.', 'Cp2.', 'Cp4.', 'Cp6.', 'Fp1.', 'Fpz.', 'Fp2.', 'Af7.', 'Af3.', 'Afz.', 'Af4.', 'Af8.', 'F7..', 'F5..', 'F3..', 'F1..', 'Fz..', 'F2..', 'F4..', 'F6..', 'F8..', 'Ft7.', 'Ft8.', 'T7..', 'T8..', 'T9..', 'T10.', 'Tp7.', 'Tp8.', 'P7..', 'P5..', 'P3..', 'P1..', 'Pz..', 'P2..', 'P4..', 'P6..', 'P8..', 'Po7.', 'Po3.', 'Poz.', 'Po4.', 'Po8.', 'O1..', 'Oz..', 'O2..', 'Iz..']
これは64個の電極を10-10法に基づいて配置したデータのようです。しかし'Fc5'のcが小文字になっていたり末尾に.がついているなど、規定の表記とは異なります。
国際10-10法に基づく電極配置図
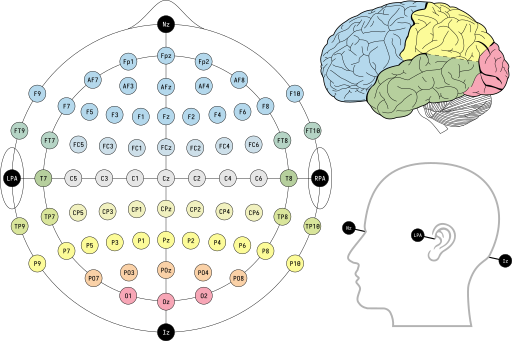
参照:Wikipedia
規定に沿った新しい電極名のリストを作成し, rawオブジェクトに反映します. 変更後の名称リストの順番を元の順番と揃えることに注意してください.
ch_names = ['FC5', 'FC3', 'FC1', 'FCz', 'FC2', 'FC4', 'FC6', 'C5', 'C3', 'C1', 'Cz', 'C2', 'C4', 'C6', 'CP5', 'CP3', 'CP1', 'CPz', 'CP2', 'CP4', 'CP6', 'Fp1', 'Fpz', 'Fp2', 'AF7', 'AF3', 'AFz', 'AF4', 'AF8', 'F7', 'F5', 'F3', 'F1', 'Fz', 'F2', 'F4', 'F6', 'F8', 'FT7', 'FT8', 'T7', 'T8', 'T9', 'T10', 'TP7', 'TP8', 'P7', 'P5', 'P3', 'P1', 'Pz', 'P2', 'P4', 'P6', 'P8', 'PO7', 'PO3', 'POz', 'PO4', 'PO8', 'O1', 'Oz', 'O2', 'Iz']
rename = {raw.ch_names[i]:ch_names[i] for i in range(len(ch_names))}
raw.rename_channels(rename)
電極の名前が規定のものと一致すれば, あとは規定のスタイルと対応付けることで位置情報を設定することができます.
raw.set_montage(mne.channels.make_standard_montage('standard_1020'))
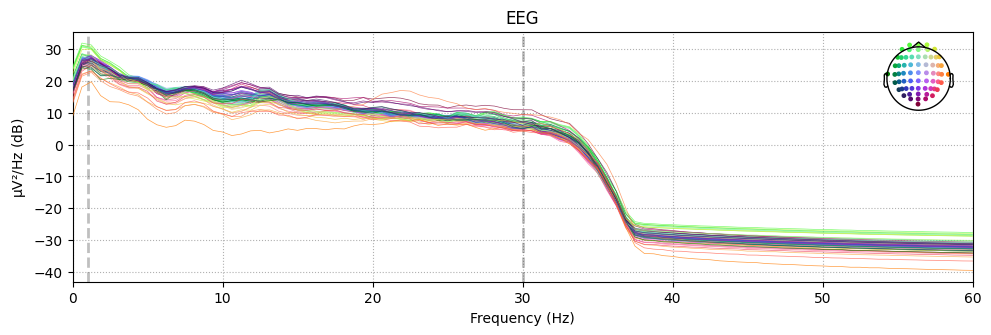
ここでもう一度, rawオブジェクトのPSDをプロットしてみましょう.
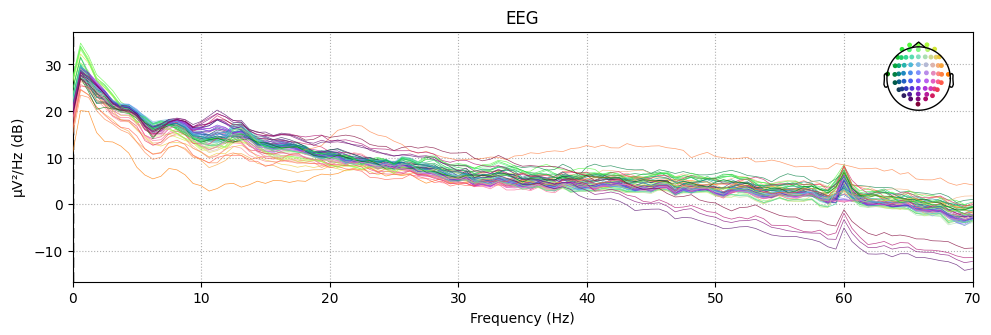
raw.compute_psd(fmin=0,fmax=60).plot()
plt.show()
電極の位置情報を設定したことでチャンネルごとに色分けされ、電極配置と対応する色が表示されました。
周波数フィルタ
続いて、周波数フィルタについて説明します。通過帯域を指定することでhigh, low, band パスフィルタを適用することができます.
試しに定常成分(0~1Hz)とγ帯域以上の成分(30Hz~)を除去するフィルタを適用します.
raw_filt = raw.copy().filter(l_freq=1, h_freq=30)
raw_filt.plot(duration=30, n_channels=4, scalings={'eeg': 200e-6})
plt.show()
raw_filt.compute_psd(fmin=0,fmax=60).plot()
plt.show()
信号からドリフトと細かいギザギザがなくなっています. また, スペクトルからも定常成分と高周波成分のパワーが減衰している様子が分かります.
その他rawオブジェクトでよく使うコード
print(raw.info['ch_names']):電極の一覧を確認
print(raw.info['sfreq']):サンプリングレートを確認
raw.pick(['channel',...]):指定した電極(C3,C4など)を選別
エポック分け
脳波を解析する際は、何らかのタスク中のデータを取り出しその間の変化に着目することが多いです。
タスクの情報をイベントとして読み込みrawオブジェクトと合わせることで、タスクごとのデータを集めたepochオブジェクトを作成できます。
まず実験中のタスクの情報を取得しましょう。実験データにイベントの情報がアノテーションされている場合以下のコードで取得できます。
events = mne.events_from_annotations(raw_filt)[0]
また、実験データにイベント情報用のチャンネルが含まれている場合は以下のコードで取得できます。
events = mne.find_events(raw, stim_channel='チャンネル名')
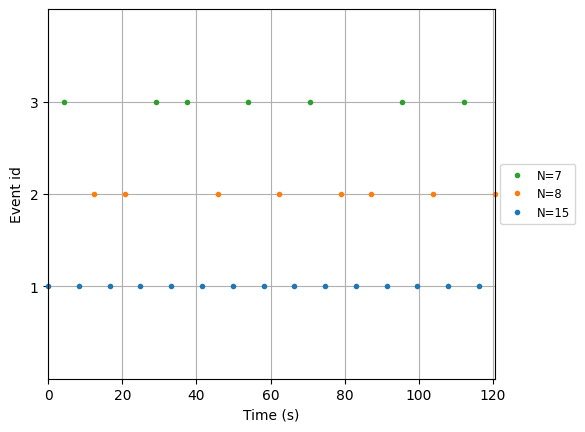
イベントを取得出来たらプロットして中身を確認することができます。
mne.viz.plot_events(events, sfreq=raw.info['sfreq'], first_samp=raw.first_samp)
plt.show()
各イベントにIDが割り振られ、どのイベントがどのタイミングで発生したか確認できます.
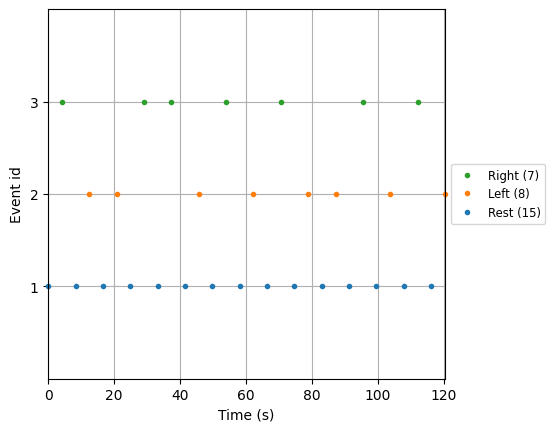
また、イベントのIDに対しラベル付けすることもできます.
このイベント情報には、安静, 左手の運動想起, 右手の運動想起が含まれているので、それぞれ'Rest', 'Left', 'Right'というようにラベル付けします.
event_dict = {'Rest': 1, 'Left': 2, 'Right': 3}
mne.viz.plot_events(events,sfreq=raw.info['sfreq'],first_samp=raw.first_samp, event_id=event_dict)
イベント情報を取得したら、それをもとにrawオブジェクトを分割しepochオブジェクトを作成できます.
epochs = mne.Epochs(raw_filt, events, event_id=event_dict, tmin=-1, tmax=2, preload=True)
-tmin, tmax:タスクの前後何秒区間を取り出すか
エポックもRawオブジェクトと同様プロットすることができます.
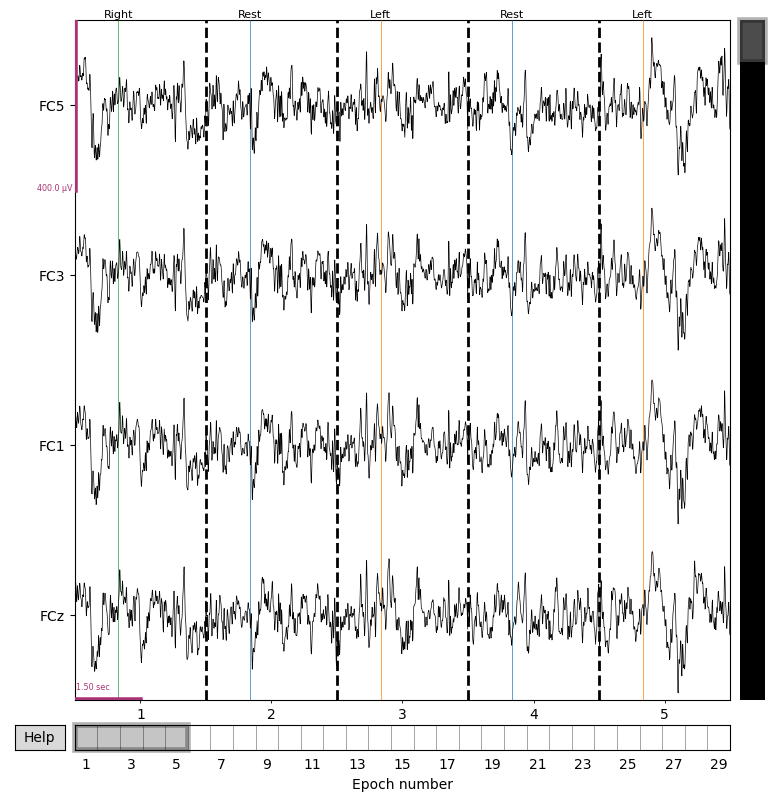
epochs.plot(n_epochs=5, n_channels=4, scalings={'eeg': 200e-6}, events=events, event_id=event_dict)
plt.show()
rawオブジェクトからイベント付近の指定した範囲のデータが取り出され, イベント情報と共に確認することができます.
また, ラベルをもとにエポックを選別することもできます。
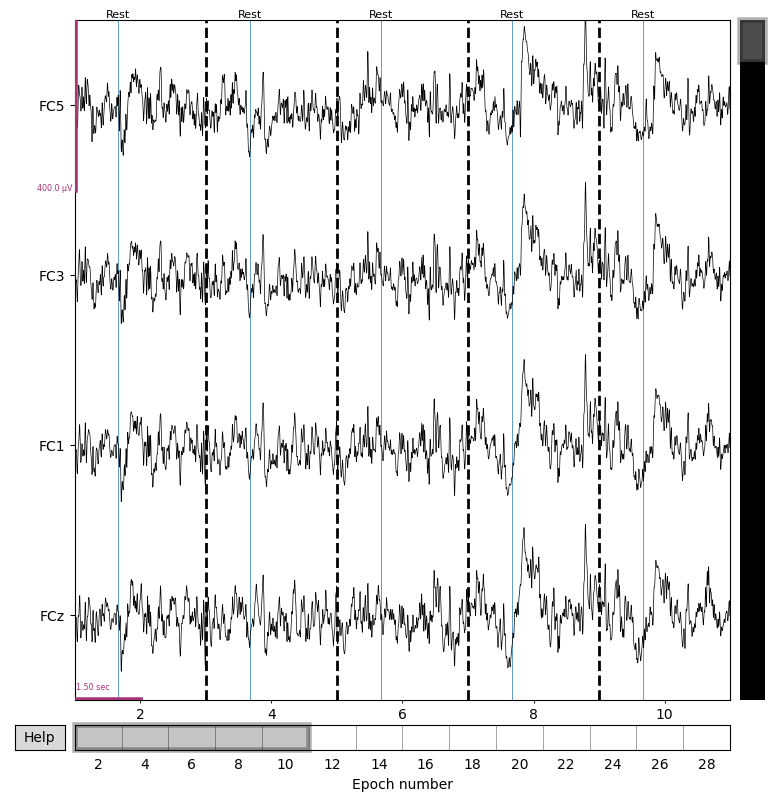
epochs_rest = epochs['Rest']
epochs_rest.plot(n_epochs=5, n_channels=4, scalings={'eeg': 200e-6}, events=events)
Rest期間のエポックのみがプロットされています。
その他epochオブジェクトでよく使うコード
print(epochs.__len__()):エポックの数を確認
epochs.crop(tmin,tmax):tmin~tmaxの時間を抽出
epochs.pick(['channel',...]):指定した電極(C3,C4など)を選別
epochs = mne.Epochs(..., reject=dict(eeg=threshold)):
threshold(40e-6など)を超えた値を含むエポックは除いてepochオブジェクトを作成
特徴抽出
エポック分けによってタスクに関係する部分の脳波を切り出すことができました。しかしエポックを直接眺めてもそれだけではタスクによる脳活動の変化を観測しているとは言えません。なぜなら、脳波には基本的にタスク由来の成分以外の背景脳波が混ざるからです. 手の動きを想起するといった思考中にも、当然それ以外の脳活動は行われています。エポック分けした脳波にもそうした背景成分は混ざるため、タスク由来の成分のみを抽出する処理が必要になります。
ここからは、MNE-Python上の信号をNumpy配列に変換し、NumpyやScipyのメソッドを用いてより詳細な解析を行う手順を紹介していきます。
Numpy配列への変換
まず、epochオブジェクトをNumpy配列に変換する方法を紹介します.
epochs_list = epochs.get_data()
print(epochs_list.shape)
---output---
(29, 64, 481)
3次元の配列が出力されており、その形状は(エポック数, チャンネル数, 時間サンプル数)となっています.
また、epochオブジェクトに含まれるイベント情報も取得できます
labels = epochs.events[:,-1]
print(labels)
---output---
[3 1 2 1 2 1 3 1 3 1 2 1 3 1 2 1 3 1 2 1 2 1 3 1 2 1 3 1 2]
時間周波数解析
Numpy配列に変換することで、Python上で提供される様々な解析ツールを自由に適用できるようになります。
ここでは、Scipyの短時間フーリエ変換メソッドstftを利用し、どのタイミング, どの周波数帯のパワーがどのように変化しているか解析します.
epochs_listにstftを適用し、各時間周波数帯でのパワー値を算出します
from scipy.signal import stft
frequencies, times, Zxx = stft(epochs_list, fs=160, nperseg=160, noverlap=120)
Zxx = np.abs(Zxx) # 振幅スペクトル
times -= 1 # 時間領域を-1~2秒に合わせる
出力された各配列frequencies, times, Zxxの形状を確認しましょう
print(frequencies.shape, times.shape, Zxx.shape)
---output---
(81,) (14,) (29, 64, 81, 14)
frequenciesには0~80Hzの周波数範囲, timesには-1~2秒の時間範囲, そしてZxxは(エポック数, 電極, 周波数, 時間)を示す配列が入っています。
続いて、タスクごとに時間周波数振幅スペクトルの加算平均(ERSP:Event-Related Spectrogram)を算出しましょう
ERSP_left = np.mean(Zxx[labels==2], axis=0)
ERSP_right = np.mean(Zxx[labels==3], axis=0)
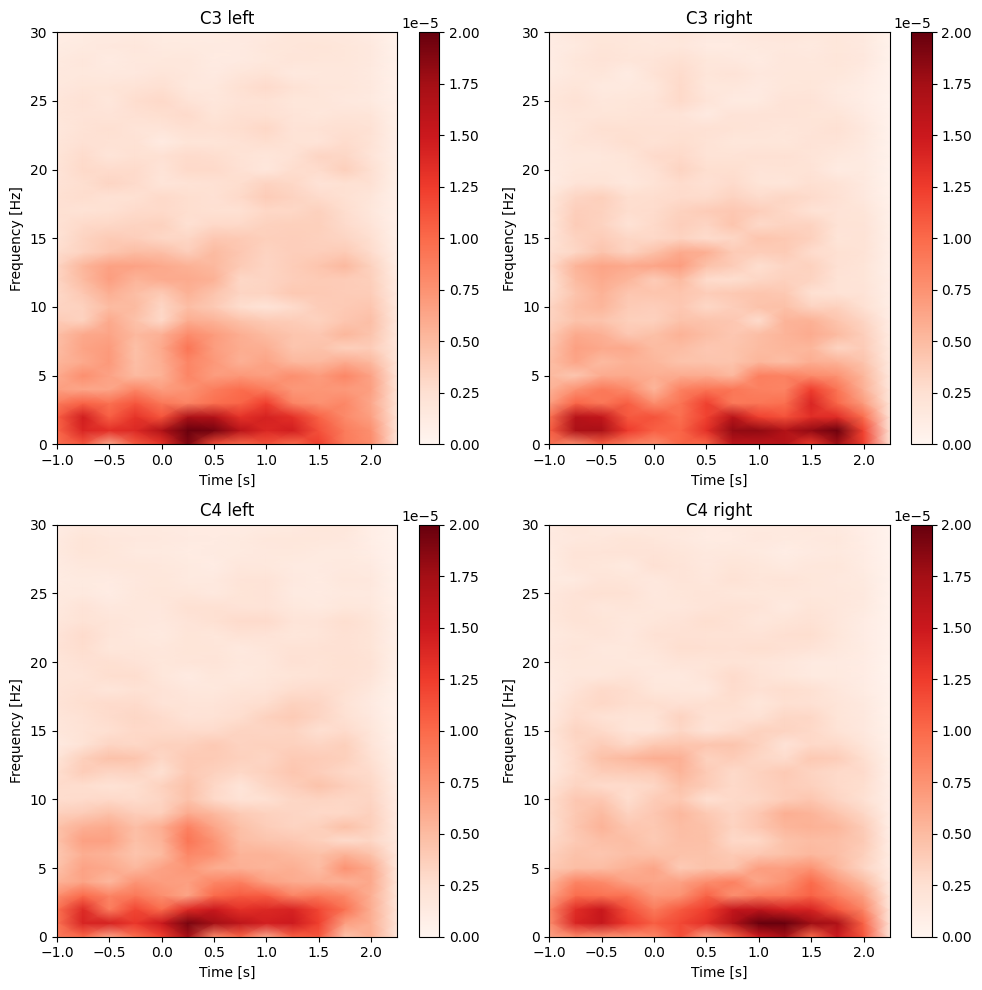
得られたERSPをプロットしてみましょう
fig, ax = plt.subplots(2,2, figsize=(10,10))
channels = ['C3','C4']
channel_index = [raw.ch_names.index(ch) for ch in channels]
labels = ['left','right']
cmaps = [ERSP_left,ERSP_right]
for i in range(4):
cmap = ax[i%2,i//2].pcolormesh(times, frequencies, cmaps[i//2][channel_index[i%2]], shading='gouraud', cmap='Reds')
ax[i%2,i//2].set_title(f'{channels[i%2]} {labels[i//2]}')
ax[i%2,i//2].set_ylim(0,30)
ax[i%2,i//2].set_ylabel('Frequency [Hz]')
ax[i%2,i//2].set_xlabel('Time [s]')
cmap.set_clim(0,20e-6)
fig.colorbar(cmap, ax=ax[i%2,i//2])
plt.tight_layout()
plt.show()
左手の運動想起と右手の運動想起で違った反応が生まれています. ただ、周波数が高くなるにつれ色合いがぼんやりしてきます。
一見、α帯やβ帯の違いは小さいように見えますが、これは帯域によるのスケールの問題です. 平均60kg程度の成人男性の体重に1kg差があるのと、平均3kg程度の赤ちゃんの体重に1kg差があるのとでは異なる意味があるように、低周波帯に1dBの違いがあるのと高周波帯に1dBの違いがあるのとでは重要度が異なります. そのため、周波数ごとに適切にスケーリングする必要があります.
事象関連(脱)同期
運動想起の解析には、事象関連(脱)同期 Event-Related (De)Synchronization (ERD/ERS)と呼ばれる指標がよく利用されます。タスク中のパワーを安静時のパワーの平均値で正規化したもので、タスクによる安静時からのパワー変化を示します。
ERD/ERS = \frac{P_{task}-P_{rest}}{P_{rest}}\times 100
では、時間周波数ごとのパワー値をこの式に沿ってERD/ERSに変換してみましょう。ここでは、タスク直前1秒間のパワーの平均値を用いて正規化します
left_rest = np.mean(ERSP_left[:,:,:len(times)//3], axis=2)[:,:,np.newaxis] #(電極, 周波数, 時間(タスク開始まで))の平均(電極, 周波数, 1)
ERD_ERS_left = (ERSP_left-left_rest)/left_rest*100
right_rest = np.mean(ERSP_right[:,:,:len(times)//3], axis=2)[:,:,np.newaxis]
ERD_ERS_right = (ERSP_right-right_rest)/right_rest*100
ERD/ERSが算出できたら、同様の手順でプロットします
(cmapの色設定を'Reds'から'RdBu_r'に変えています)
fig, ax = plt.subplots(2,2, figsize=(10,10))
channles = ['C3','C4']
channel_index = [raw.ch_names.index(ch) for ch in channles]
labels = ['left','right']
cmaps = [ERD_ERS_left,ERD_ERS_right]
for i in range(4):
cmap = ax[i%2,i//2].pcolormesh(times, frequencies, cmaps[i//2][channel_index[i%2]], shading='gouraud', cmap='RdBu_r')
ax[i%2,i//2].set_title(f'{channles[i%2]} {labels[i//2]}')
ax[i%2,i//2].set_ylim(0,30)
ax[i%2,i//2].set_ylabel('Frequency [Hz]')
ax[i%2,i//2].set_xlabel('Time [s]')
cmap.set_clim(-100,100)
fig.colorbar(cmap, ax=ax[i%2,i//2])
plt.tight_layout()
plt.show()
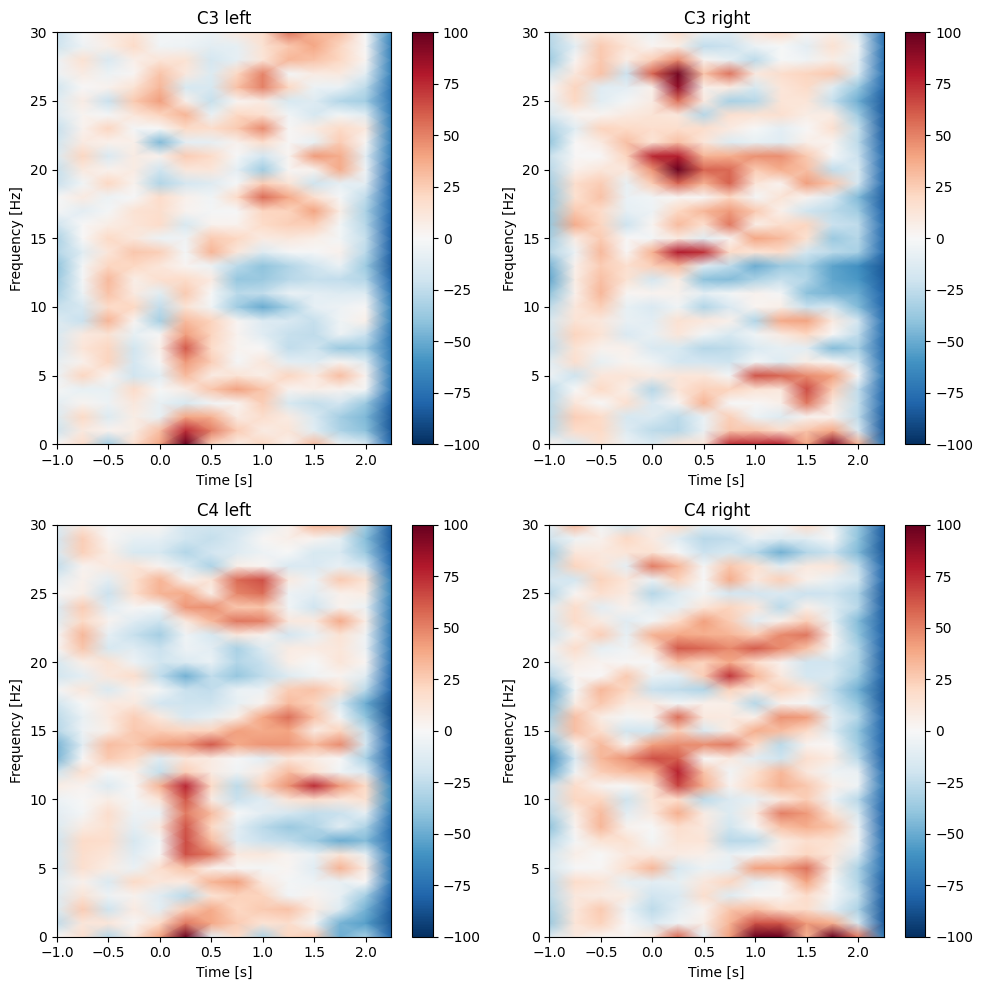
ERD/ERSを算出することで、高周波帯の違いも明瞭に可視化することができました
青色の部分が安静時に比べてパワーが減った領域(ERD:事象関連脱同期), 赤色の部分が安静時に比べてパワーが増加した領域(ERS:事象関連同期)にあたります
では、α帯(8~13Hz), β帯(13Hz~)で平均したERD/ERSの時間変化をプロットしてみましょう
ERD_ERS_left_alpha = np.mean(ERD_ERS_left[:,(frequencies>=8)&(frequencies<=13)], axis=1) #(電極, 周波数(α帯域), 時間)の平均(電極, 時間)
ERD_ERS_right_alpha = np.mean(ERD_ERS_right[:,(frequencies>=8)&(frequencies<=13)], axis=1)
ERD_ERS_left_beta = np.mean(ERD_ERS_left[:,(frequencies>=14)&(frequencies<=30)], axis=1) #(電極, 周波数(β帯域), 時間)の平均(電極, 時間)
ERD_ERS_right_beta = np.mean(ERD_ERS_right[:,(frequencies>=14)&(frequencies<=30)], axis=1)
fig, ax = plt.subplots(2,2, figsize=(10,10))
bands = ['α','β']
channles = ['C3','C4']
channel_index = [raw.ch_names.index(ch) for ch in channles]
ERD_ERSs = [[ERD_ERS_left_alpha,ERD_ERS_right_alpha],[ERD_ERS_left_beta,ERD_ERS_right_beta]]
for i in range(4):
ax[i%2,i//2].plot(times, ERD_ERSs[i%2][0][channel_index[i//2]], label='left')
ax[i%2,i//2].plot(times, ERD_ERSs[i%2][1][channel_index[i//2]], label='right')
ax[i%2,i//2].set_title(f'{bands[i%2]} {channles[i//2]}')
ax[i%2,i//2].set_ylim(-50,50)
ax[i%2,i//2].set_ylabel('ERD/ERS [%]')
ax[i%2,i//2].set_xlabel('Time [s]')
ax[i%2,i//2].vlines(0, -100, 100, "black")
ax[i%2,i//2].legend()
plt.tight_layout()
plt.show()
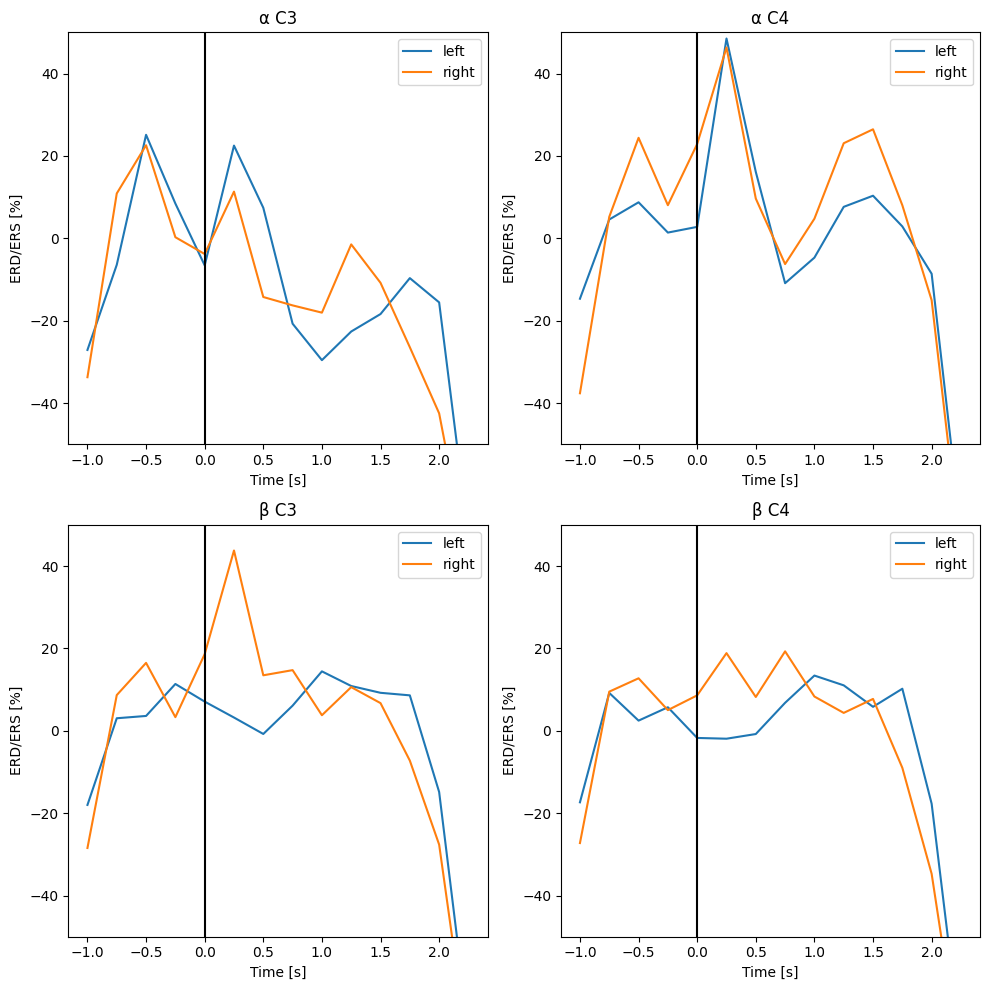
参照論文の図と同様に、左右の運動想起に対するα,β帯のERD/ERSを算出できました ...のですが、参照論文のような、動きを想起した腕の反対側の電極でパワーが減少するという様子は見られません.
考えられる原因として、解析したデータに含まれる試行数が不足していることが挙げられます. イベント情報から分かるように、このデータには想起タスクが左右それぞれで10回も含まれていません。
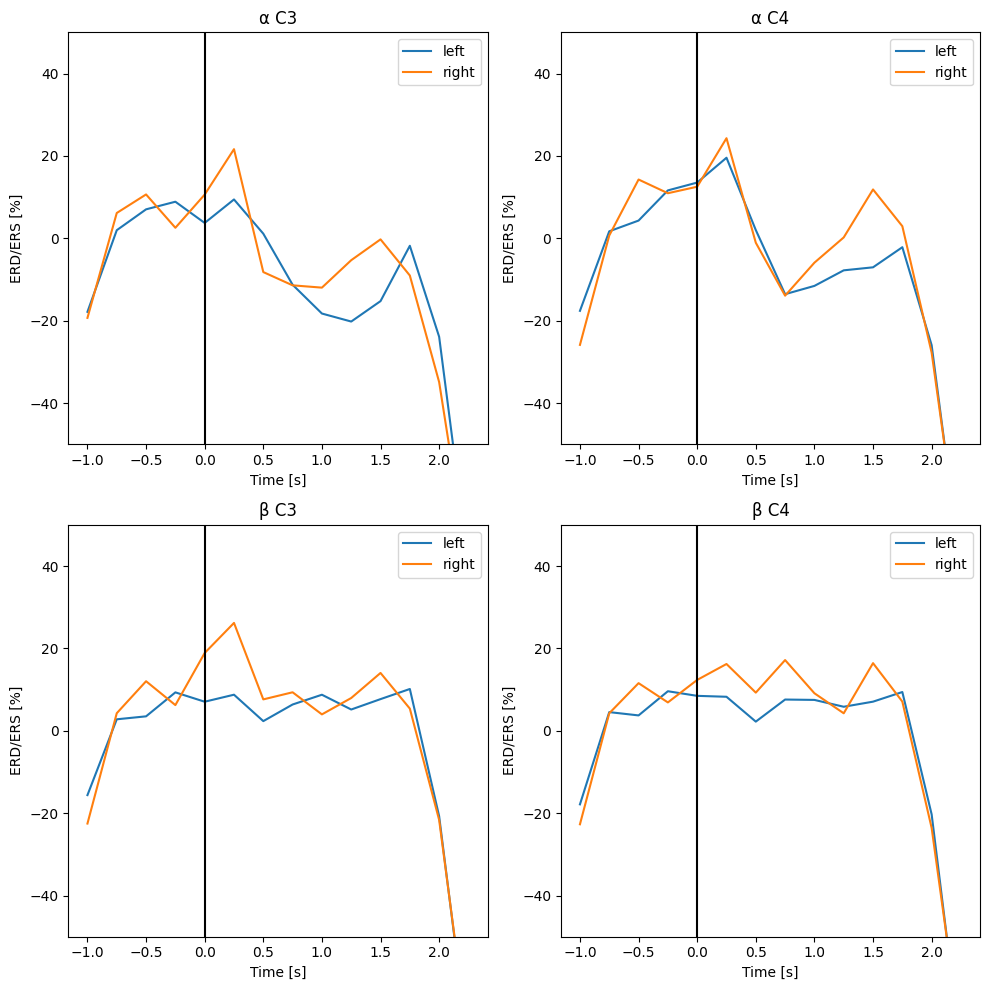
同被験者の別セッションのデータである、S001R08, S001R12のデータも含めて解析を行うと以下のような結果になります。
...それでも参照論文の結果とは似つきません。 というのも、こうしたBCIのタスクは反応に個人差があり、個人の特性やタスクの習熟度によって結果が大きく変化すると言われています。
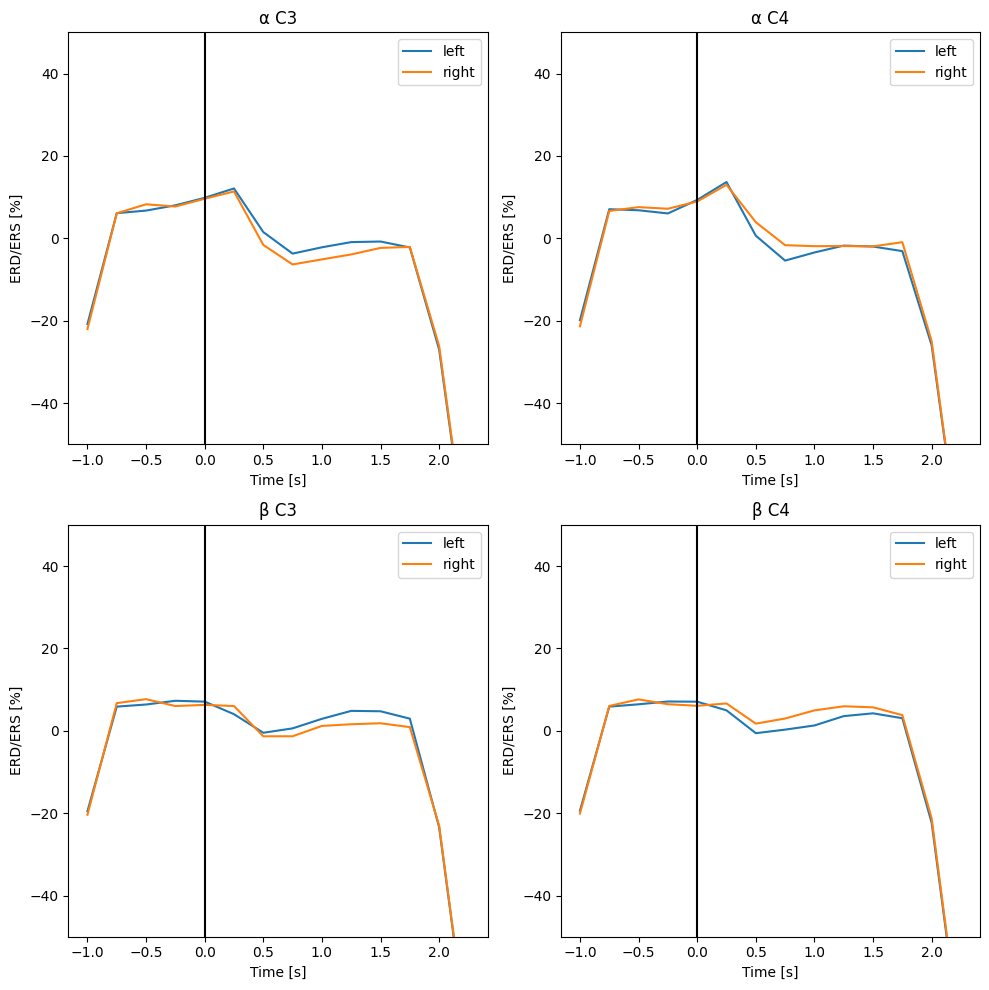
例えば、本データセットに含まれる109人のデータすべてのエポックを解析し、平均したERS/ERDを算出すると以下のようになります。
想起した腕の反対側の電極でよりパワーが減少する様子を確認できます。109人と言わずとも、10人程度の被験者のエポックを平均しても近しい結果は得られるので是非試してみてください。
Numpy配列からMNE-Pythonオブジェクトを作成
Numpy配列に変換することで自由度の高い解析ができるのは利点ですが、後でまたMNE-Pythonのメソッドを使った処理を行いたい場合もあります。そこで本節では、Numpy配列からMNE-Pythonのオブジェクトを作成する方法を紹介します
本節では算出したERD_ERSをevokedオブジェクトに変換し、そのパワーの頭皮分布をプロットしてみます。
evokedオブジェクトの作成
まず、Numpy配列からMNE-Pythonオブジェクトに変換するためには、電極の名前, サンプリングレート, 計測機器の種類(EEG,MEG...)を示したinfoオブジェクトを用意する必要があります. 今回の場合, 電極の名前や機器はそのままですが、サンプリングレートに関しては時間周波数解析の窓幅, 重複幅によって変化している点に注意が必要です
info = mne.create_info(ch_names = raw.ch_names, sfreq = len(times)//(times[-1]-times[0]), ch_types='eeg')
evokedオブジェクトは、(電極数, 時間サンプル数)の形状を持つNumpy配列, infoオブジェクト, 開始時間を入力することで作成できます
evoked_left = mne.EvokedArray(ERD_ERS_left_alpha, info, tmin=times[0])
evoked_right = mne.EvokedArray(ERD_ERS_right_alpha, info, tmin=times[0])
また、最初rawオブジェクトに適用したように電極の配置を設定しましょう
evoked_left.set_montage(mne.channels.make_standard_montage('standard_1020'))
evoked_right.set_montage(mne.channels.make_standard_montage('standard_1020'))
この状態で一度evokedオブジェクトをプロットしてみましょう
evoked_left.plot()
plt.show()
evoked_right.plot()
plt.show()
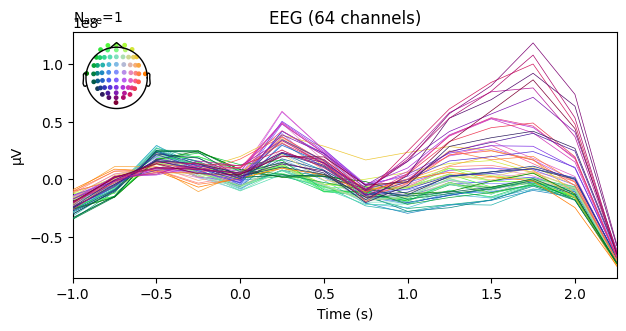
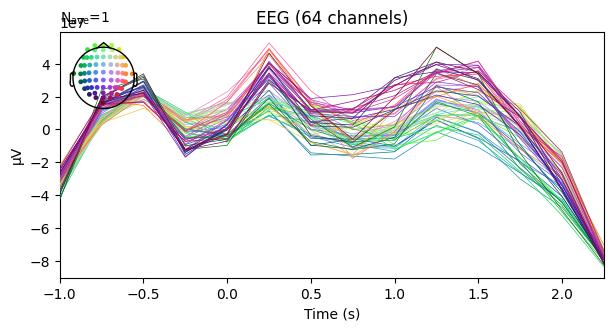
ERD/ERSをevokedオブジェクトの形式でプロットできました
トポグラフィーのプロット
それでは、ERD/ERSの頭皮分布をプロットしてみましょう. プロットする時間サンプルとカラーマップの範囲などを自由に指定できます.
plot_times = np.arange(-1, 2, 0.5)
evoked_left.plot_topomap(times=plot_times, ch_type='eeg', time_unit='s', vlim=[-100,100], scalings=dict(eeg=1), units =f'[%]')
plt.show()
evoked_right.plot_topomap(times=plot_times, ch_type='eeg', time_unit='s', vlim=[-100,100], scalings=dict(eeg=1), units =f'[%]')
plt.show()
ちなみに、全被験者で平均したERD/ERSのトポグラフィーはこちらのようになります.


電極C3,C4だけでなく運動野付近全般で脱同期が発生し、また想起方向の逆側でより強い脱同期が起きている様子が窺えます。
あとがき
運動想起方向の違いによる脳波の違いを公開されているデータセットを使って実際に解析する手順を紹介しました。
想起する腕の反対側の電極のパワーが顕著に減少するという興味深い特性を観察できましたが、何人もの被験者の何十回ものデータを平均してようやく違いが分かるという結果でした。実際ブレイン・コンピュータ・インターフェースとして実用するには一つのエポックからタスクの違いを見分けたいところです。
そのためには、より強力に脳波の特性を抽出する信号処理を行う必要があります。例えば、今回は特段気にしませんでしたが、頭皮で観察される脳波は、基本的に眼球運動などによるノイズで汚染されています。また、今回は特にC3,C4の2つの電極に着目しましたが、他の電極でもタスクによる違いは生まれているので、それらの情報も活用できそうです。また、注目する特徴を個人に合わせることもできそうです。
今回は見送りましたが、MNE-Pythonにはノイズ除去, 複数電極を用いた空間フィルタを使うためのメソッドも用意されており、そのチュートリアルも用意されています。
MNE-Pythonのチュートリアルはプログラムの使い方に留まらず脳波解析の様々なエッセンスが詰まっています。サイト内検索などを活用し目を通すことをおすすめします。今後それらの日本語解説記事を書くかもしれません。