クイックソート
ピボットを決めて、そのピボットより、小さい値、大きい値でグループ分けする。それを再帰的に繰り返す。
ピボットの値をどこにするかで計算量が変わってくる。
const quickSort = (arr) => {
if (!arr.length) {
return arr;
}
const pivot = arr[0];
const minArr = arr.filter(arr => arr < pivot);
const maxArr = arr.filter(arr => arr > pivot);
return [...quickSort(minArr), pivot, ...quickSort(maxArr)];
}
const arr = quickSort([8,41,6,4,2,19]);
console.log(arr);
// [ 2, 4, 6, 8, 19, 41 ]
選択ソート
配列を線形探索し、その中での最小値を一番左に移動する。
これで、配列の中で最小の値は一番左に移動する。
そうしたら、探索するスタート地点を一つ右に進めて、再度配列を線形探索し、その中での最小値を左に移動し、、というのを繰り返す。
const searchMinIndex = (
arr: number[],
minIndex: number,
curIndex: number
): number => {
if (curIndex === arr.length) {
return minIndex
}
if (arr[minIndex] > arr[curIndex]) {
minIndex = curIndex
}
return searchMinIndex(arr, minIndex, curIndex + 1)
}
const _selectionSort = (arr: number[], start: number): number[] => {
if (start === arr.length) {
return arr
}
let minIndex = searchMinIndex(arr, start, start)
let tmp = arr[start]
arr[start] = arr[minIndex]
arr[minIndex] = tmp
return _selectionSort(arr, start + 1)
}
const selectionSort = (arr: number[]) => {
const start = 0
return _selectionSort(arr, start)
}
selectionSort([3, 4, 6, 5, 3, 88, 90, 0]) // [0, 3, 3, 4, 5, 6, 88, 90]
バブルソート
隣接する数字同士を比較し、交換していく。
比較する二つの数値は i と i+1 のインデックスの数値を比較していく。
以下の例では i の初期値は 0 なので、配列の先頭から比較をしていく。
比較が終われば i を一つ増やし、再度比較をする。その比較を探索範囲(size)の中で繰り返しおこなう。
探索範囲(size)の初期値は配列の要素数なので、初回の探索範囲(size)での比較では、引数で渡した配列の中での最高値が右端へ移動する。
このように探索範囲(size)での比較一回につき、右端の数値はソート済みの状態になるので、次は探索範囲(size)を一つ狭めて、再度ソート処理を行っていく。
このソート処理を繰り返し、探索範囲が 1 まで狭まればソート完了。
const _bubbleSort = (arr: number[], size: number, i: number = 0) => {
if (size > 1) {
if (i < size - 1) {
if (arr[i] > arr[i + 1]) {
const tmp = arr[i + 1]
arr[i + 1] = arr[i]
arr[i] = tmp
}
_bubbleSort(arr, size, i + 1)
}
_bubbleSort(arr, size - 1, 0)
}
return arr
}
const bubbleSort = (arr: number[], i: number = 0) => {
return _bubbleSort(arr, arr.length, i)
}
const arr = [3, 4, 6, 1, 7, 2]
bubbleSort(arr) // [1, 2, 3, 4, 6, 7]
シェイカーソート
バブルソートの双方向版。
上述のバブルソートでは昇順に隣接する値の比較/交換を繰り返していたが、シェイカーソートでは
昇順に隣接する値を比較/交換した後は、降順に隣接する値を比較/交換していく。
const shakerSortASC = (arr: number[], start: number, end: number) => {
if (start < end) {
if (arr[start] > arr[start + 1]) {
swap(start, start + 1, arr)
}
shakerSortASC(arr, start + 1, end)
}
return arr
}
const shakerSortDESC = (arr: number[], start: number, end: number) => {
if (end > start) {
if (arr[end - 1] > arr[end]) {
swap(end - 1, end, arr)
}
shakerSortDESC(arr, start, end - 1)
}
return arr
}
function swap(left: number, right: number, arr: number[]) {
let tmp = arr[left]
arr[left] = arr[right]
arr[right] = tmp
}
const shakerSort = (arr: number[]) => {
// 探索範囲の初期値
let start = 0
let end = arr.length - 1
while (true) {
arr = shakerSortASC(arr, start, end)
end-- // shakerSortASC を一回行うと、最大値が一つ確定するので、探索範囲を一つ狭める
if (start === end) { // 探索範囲が0になっていたら、ソート完了
break
}
arr = shakerSortDESC(arr, start, end)
start++ // shakerSortDESC を一回行うと、最小値が一つ確定するので、探索範囲を一つ狭める
if (start === end) { // 探索範囲が0になっていたら、ソート完了
break
}
}
return arr
}
shakerSort([3, 4, 6, 5, 3, 88, 90, 0]) // [0, 3, 3, 4, 5, 6, 88, 90]
バケットソート
配列の添字を利用したソート。
bucket 配列を用意し、ソート対象の配列に 3 という数値があったら
bucket[3] = 1
をする。再度 3 が出てきたら、
bucket[3]++
をする。これにより、 bucket[3] にはソート対象の配列に 3 がいくつあるかのカウントがされていく。
他の数値でも同様の処理を行い、bucket 配列の添字の順番で数字を並べれば(カウントの回数分繰り返しながら)ソートされた状態の配列になる。
function bucketSort(arr: number[]) {
const bucket = []
for (let i = 0; i < arr.length; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 1
} else {
bucket[arr[i]]++
}
}
const res = []
for (let i = 0; i < bucket.length; i++) {
if (!bucket[i]) {
continue
}
for (let j = 0; j < bucket[i]; j++) {
res.push(i)
}
}
return res
}
bucketSort([3, 4, 6, 5, 3, 88, 90, 0]) // [0, 3, 3, 4, 5, 6, 88, 90]
挿入ソート
配列から一つ値を取り出し、その値を正しい位置に移動させていくソート。
下記の例のイメージは以下のような感じ
- 配列のインデックスが 1 と 0 の値を比較し、昇順ではなかったらswap
- インデックスが 0 と 1 の値は昇順に並び替えれたので、次は 「2 と 1」 、「1 と 0」 のインデックスの値の比較/swap を行う
- インデックスが 0 と 1 と 2 の値は昇順に並び替えれたので、次は 「3 と 2」 、「2 と 1」、「1 と 0」 のインデックスの値の比較/swap を行う
- これを、比較の開始位置が配列の要素数と同じ数になるまで繰り返す。
const swap = (arr: number[], index: number, index2: number) => {
const tmp = arr[index]
arr[index] = arr[index2]
arr[index2] = tmp
}
const sort = (arr: number[], cur: number): void => {
if (cur === 0) {
return
}
const prev = cur - 1
if (arr[cur] > arr[prev]) {
return
} else {
swap(arr, prev, cur)
}
return sort(arr, cur - 1)
}
const _insertionSort = (arr: number[], cur: number): number[] => {
if (cur === arr.length) {
return arr
}
sort(arr, cur)
return _insertionSort(arr, cur + 1)
}
const insertionSort = (arr: number[]) => {
const start = 1
return _insertionSort(arr, start)
}
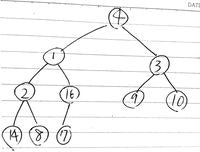
insertionSort([4, 1, 3, 2, 16, 9, 10, 14, 8, 7]) // [1, 2, 3, 4, 7, 8, 9, 10, 14, 16]
マージソート
まず、配列を限界までグループ分けし、それぞれのグループが値一つにまで細分化させる。
下記の例だと、[4, 1, 3, 2, 16, 9, 10, 14, 8, 7] の並び替えなので、
[4]、[1]、[3]、[2]、[16]、[9]、[10]、[14]、[8]、[7] というグループ分けになる。
この状態で、
- [4] と [1] のグループを比較、昇順で並び替えて、[1, 4] のグループを作成
- [2] と [16] のグループを比較、昇順で並び替えて、[2, 16] のグループを作成
- [3] と [2, 16] のグループを比較、昇順で並び替えて、[3, 2, 16] のグループを作成
のような感じで、細分化したグループ同士で比較、並び替えを行い、最終的に一つのグループになるまで、処理を行う。
参考:https://ichi.pro/javascript-de-no-ma-jiso-toarugorizumu-54999356457056
function mergeSort(unsortedArray: number[]): number[] {
if (unsortedArray.length <= 1) {
return unsortedArray
}
const middle = Math.floor(unsortedArray.length / 2)
const left = unsortedArray.slice(0, middle)
const right = unsortedArray.slice(middle)
return merge(mergeSort(left), mergeSort(right))
}
function merge(left: number[], right: number[]): number[] {
let resultArray = [],
leftIndex = 0,
rightIndex = 0
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
resultArray.push(left[leftIndex])
leftIndex++
} else {
resultArray.push(right[rightIndex])
rightIndex++
}
}
return resultArray
.concat(left.slice(leftIndex))
.concat(right.slice(rightIndex))
}
mergeSort([4, 1, 3, 2, 16, 9, 10, 14, 8, 7]) // [1, 2, 3, 4, 7, 8, 9, 10, 14, 16]
バイトニックソート
並列処理が可能なソート
const bitonicSort = (asc, arr) => {
if (arr.length <= 1) {
return arr;
}
const midPoint = arr.length / 2;
const first = bitonicSort(true, arr.slice(0, midPoint));
const second = bitonicSort(false, arr.slice(midPoint, arr.length));
return _subSort(asc, [...first, ...second]);
};
const _subSort = (asc, arr) => {
if (arr.length === 1) {
return arr;
}
_compareAndSwap(asc, arr);
const midPoint = arr.length / 2;
const first = _subSort(asc, arr.slice(0, midPoint));
const second = _subSort(asc, arr.slice(midPoint, arr.length));
return [...first, ...second];
};
const _compareAndSwap = (asc, arr) => {
const dist = arr.length / 2;
for (let i = 0; i < dist; i++) {
// 左側が右側より大きいかつ、昇順に並び変えたいならswapする
if (arr[i] > arr[i + dist] === asc) {
[arr[i], arr[i + dist]] = [arr[i + dist], arr[i]];
}
}
};
bitonicSort(false, [
89,
28,
7,
3,
65,
99,
57,
18,
56,
63,
32,
69,
73,
93,
71,
30,
]); // [ 99, 93, 89, 73, 71, 69, 65, 63, 57, 56, 32, 30, 28, 18, 7, 3 ]
bitonicSort(true, [
89,
28,
7,
3,
65,
99,
57,
18,
56,
63,
32,
69,
73,
93,
71,
30,
]); // [ 3, 7, 18, 28, 30, 32, 56, 57, 63, 65, 69, 71, 73, 89, 93, 99 ]
処理のイメージはこんな感じ。
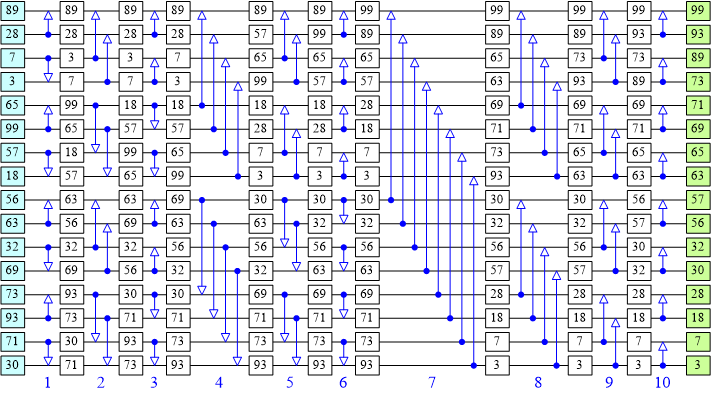
(上記画像はquoraにあったものから引用)
ビット全探索
ビット演算を用いて全組み合わせを列挙し、探索する。
以下の例は、第一引数で渡された数値群から、第二引数で渡された数値になるような組み合わせが存在するか返す。
const main = (input: number[], ans: number) => {
const n = input.length;
for (let i = 0; i < (1 << n); i++) {
let sum = 0;
for (let j = 0; j < n; j++) {
console.log(i, j, !!((i >> j) & 1))
if (!((i >> j) & 1)) continue;
sum += input[j];
}
if (sum === ans) {
return true
}
}
return false
}
main([2,5,10], 16) // false
main([2,5,9], 16)) // true
main([11,5,0], 16)) // true
main([4,16,10], 16) // true
main([1,1,1], 16) // false
上記コードの console.log(i, j, !!((i >> j) & 1)) の出力は以下のようになる。
3つある数値の選ぶ/選ばないのパターンが羅列されていることがわかる。
数値を選ぶ場合(1の場合)、 sum にその値を加算し、第二引数で渡された期待する合計値と同じかどうか判定している。
0 0 false // 000
0 1 false
0 2 false
1 0 true // 100
1 1 false
1 2 false
2 0 false // 010
2 1 true
2 2 false
3 0 true // 110
3 1 true
3 2 false
4 0 false // 001
4 1 false
4 2 true
5 0 true // 101
5 1 false
5 2 true
6 0 false // 011
6 1 true
6 2 true
7 0 true // 111
7 1 true
7 2 true
シフト処理は馴染みがないと処理のイメージがつきにくいので、さらに深堀。
(1 << n) は 1 のビットを n の数だけ左シフトする。
n が 3 の場合は 8 が返る。(1 << n) は 2^n と等しい。(下記参照)
const one = 1; // 00000000000000000000000000000001
const n = 3; // 00000000000000000000000000000011
// 0001 を 3つ左にシフトしたら 1000
console.log(one << n); // 00000000000000000000000000001000 => 8
3桁の各桁を選ぶ、選ばないのパターンは 000、100、010、110、001、101、011、111の8パターンあるので、全パターン数がこれで求めれた。
全パターン数は求めれたが、次は「それを選ぶ、選ばない」を表現する必要がある。
それをやってるのが (i >> j) & 1 。これは i のビットを j の数だけ右シフトする。
console.log(i, j, !!((i >> j) & 1)) の結果が 7 0 true だった時を考える。
const i = 7; // 00000000000000000000000000000111
const j = 0; // 00000000000000000000000000000000
console.log(i >> j); // 00000000000000000000000000000111 => 7 (シフトする数は 0 なので、値は変わらず)
// & は両方のビットが立ってるものが立つので、 111 と 001 を & すると 001 となる
const one = 1 // 00000000000000000000000000000001
console.log((i >> j) & 1) // 00000000000000000000000000000001 => 1
console.log(i, j, !!((i >> j) & 1)) の結果が 6 0 false だった時を考える。
const i = 6; // 00000000000000000000000000000110
const j = 0; // 00000000000000000000000000000000
console.log(i >> j); // 00000000000000000000000000000110 => 6 (シフトする数は 0 なので、値は変わらず)
// & は両方のビットが立ってるものが立つので、 110 と 001 を & すると 000 となる
const one = 1 // 00000000000000000000000000000001
console.log((i >> j) & 1) // 00000000000000000000000000000000 => 0
console.log(i, j, !!((i >> j) & 1)) の結果が 5 1 false だった時を考える。
const i = 5; // 00000000000000000000000000000101
const j = 1; // 00000000000000000000000000000001
console.log(i >> j); // 00000000000000000000000000000010 => 2 (右シフトしてあぶれたビットは廃棄される)
// & は両方のビットが立ってるものが立つので、 010 と 001 を & すると 000 となる
const one = 1 // 00000000000000000000000000000001
console.log((i >> j) & 1) // 00000000000000000000000000000000 => 0
このように (i >> j) & 1 の結果によって、選ぶ、選ばないのパターンを表現できる。
幅優先探索
以下のコードは START から始まって TARGET にを見つけるまで、幅優先探索をするコード。
START がグラフの頂点で、そこからは alice, bob, claire にたどることができ、この3人が頂点から一番近い。
alice からは peggy へたどることができ、これは頂点(START)から 2 離れている。
START からグラフを辿っていき、 TARGET へ辿り着くのに、幅優先探索を使った場合、どういう経路を辿ったかを console.log で出している。
グラフをたどる際、一度探索した場所は探索する必要がない。
まだ探索してない場所を探索し続ける必要があるが、それをキュー(FIFO)を使って実現している。
キューにあるものはまだ未探索のもの、探索したものはキューから出していく、といった感じ。
頂点からの距離が近いものから探索していくという動作になる。
イメージ的には、現在探索しているノードに紐づくノードを確認しきってから(幅優先)、次のノードの探索に移る、という動きになる。
const graph = {};
graph['START'] = ['alice', 'bob', 'claire'];
graph['bob'] = ['anuj', 'peggy'];
graph['alice'] = ['peggy'];
graph['claire'] = ['TARGET', 'jonny'];
graph['anuj'] = [];
graph['peggy'] = [];
graph['thom'] = [];
graph['jonny'] = [];
const bfs = () => {
const queue = graph['START'];
while (queue.length) {
const person = queue.shift();
console.log(person);
if (person === 'TARGET') {
return;
} else {
queue.push(...graph[person])
}
}
console.log('見つからなかった。')
return;
}
bfs();
// alice
// bob
// claire
// peggy
// anuj
// peggy
// TARGET
幅優先探索では、各ノードがグラフの頂点からどれくらい離れているかを求めることができる。
dist は各頂点が START からどれくらい離れているかを記録したデータ。dist["頂点"] で "頂点" がどれくらいSTARTから離れているかがわかる。
queue は 「発見済みだが未訪問」 の頂点を格納するキュー。
新しい頂点を発見した際は、 dist へ距離を記録し、その頂点をキューに格納する。そして、次以降のループでその頂点をキューから取り出して訪問していくイメージ。
const graph: Record<string, string[]> = {}
graph['START'] = ['alice', 'bob', 'claire']
graph['bob'] = ['anuj', 'peggy']
graph['alice'] = ['peggy']
graph['claire'] = ['TARGET', 'jonny']
graph['anuj'] = []
graph['peggy'] = []
graph['thom'] = []
graph['jonny'] = []
const bfs = () => {
const dist: Record<string, number> = {}
const queue = []
dist['START'] = 0 // START は開始地点なので距離は 0 で初期化
queue.push('START') // 最初に訪問する頂点として START をセットする。
while (queue.length) {
const person = queue.shift()
if (person && graph[person]) {
graph[person].forEach((p) => {
if (dist[p]) {
return // すでに発見済みならスルー
}
dist[p] = dist[person] + 1 // 新たに発見したノードのSTARTからの距離を記録
queue.push(p) // 新たに発見したノードを未探索キューに入れる
})
}
}
console.log(dist)
}
bfs()
//{
// "START": 0,
// "alice": 1,
// "bob": 1,
// "claire": 1,
// "peggy": 2,
// "anuj": 2,
// "TARGET": 2,
// "jonny": 2
//}
深さ優先探索
以下のコードは START から始まって TARGET を見つけるまで、深さ優先探索をするコード。
幅優先探索ではキューを使ったが、それをスタックを利用するようにしただけ。
スタック(LIFO)を使うことで、後から追加したノードから確認するようになるので、終端まで探索してから(深さ優先)、次の頂点に進んでいく探索ができる。
深さ優先探索では、その場所に到達できるかどうかは判別できるが、その場所が頂点からどれだけ離れているかは求めることができない。
const graph = {};
graph['START'] = ['alice', 'bob', 'claire'];
graph['bob'] = ['anuj', 'peggy'];
graph['alice'] = ['peggy'];
graph['claire'] = ['TARGET', 'jonny'];
graph['anuj'] = [];
graph['peggy'] = [];
graph['thom'] = [];
graph['jonny'] = [];
const dfs = () => {
const queue = graph['START'];
while (queue.length) {
const person = queue.pop();
console.log(person);
if (person === 'TARGET') {
return
} else {
queue.push(...graph[person])
}
}
console.log('見つからなかった。')
return
}
dfs();
// claire
// jonny
// TARGET
上のコードを再帰で書いたパターンが以下。
const dfs = (queue) => {
if (!queue.length) {
console.log('見つからなかった。')
}
const person = queue.pop();
console.log(person)
if (person === 'TARGET') {
return
} else {
queue.push(...graph[person])
}
return dfs(queue)
}
dfs(graph['START']);
// claire
// jonny
// TARGET
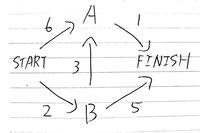
ダイクストラ
- それぞれのノードはスタート地点からのコストを持つ。開始時はスタート地点は0、他のノードはコストが不明なのでInfinity
- 最もコストが低く、まだ確認していないノードを探す
- そのノードの隣接ノードを探す。
- 隣接ノードの現在のコストと、今いる場所から隣接ノードへ辿った場合のコストを比較し少ない方で隣接ノードのコストを更新する。
- 現在のノードを確認済みにし、次のノードへ移動する。
- 全てのノードが確認済みになるまで続ける。
ダイクストラは負のコストが存在するグラフの場合、正しく計算できなくなる。負の値が存在する場合はベルマンフォードを使う。
const findLowestCostNode = (nodeList) => {
const unProcessedNodeList = nodeList.filter(node => !node.processd);
return unProcessedNodeList.reduce((nodeA, nodeB) => {
if (nodeA.cost <= nodeB.cost) {
return nodeA;
} else {
return nodeB
}
}, {});
}
const findNode = (nodeList, targetNodeName) => {
return nodeList.find(node => node.name === targetNodeName);
}
const _display = (nodeList, node, routes) => {
if (node.parents.name === 'start') {
const startNode = findNode(nodeList, 'start');
routes.push(startNode);
console.log(routes.reverse());
return;
}
const parentsNode = findNode(nodeList, node.parents.name);
routes.push(parentsNode);
_display(nodeList, parentsNode, routes);
}
const displayResult = (nodeList) => {
const finNode = nodeList.find(node => node.name === 'fin');
_display(nodeList, finNode, [finNode]);
}
const dijkstra = (nodeList) => {
// 未処理かつ、コストが一番低いノードを取得
let node = findLowestCostNode(nodeList);
while (Object.keys(node).length) { // 未処理のノードがある限り続ける
const neighbors = graph[node.name];
Object.keys(neighbors).forEach(nodeName => {
const newCost = node.cost + neighbors[nodeName]; // 経由した場合のコスト
const neighborNode = findNode(nodeList, nodeName);
const currentCost = neighborNode.cost; // 現在登録されているコスト
if (currentCost > newCost) {
neighborNode.cost = newCost;
neighborNode.parents = node;
}
});
node.processd = true;
node = findLowestCostNode(nodeList);
}
displayResult(nodeList);
}
const graph = {
start: {
a: 6,
b: 2
},
a: {
fin: 1,
},
b: {
a: 3,
fin: 5
},
fin: {} // ゴールには隣接ノードはない
}
class Node {
constructor({ name, cost }) {
this.name = name;
this.cost = cost;
this.parents = {};
this.processd = false;
}
}
const start = new Node({ name: 'start', cost: 0 })
const a = new Node({ name: 'a', cost: Infinity })
const b = new Node({ name: 'b', cost: Infinity })
const fin = new Node({ name: 'fin', cost: Infinity })
dijkstra([start, a, b, fin]);
// [ Node { name: 'start', cost: 0, parents: {}, processd: true },
// Node {
// name: 'b',
// cost: 2,
// parents: Node { name: 'start', cost: 0, parents: {}, processd: true },
// processd: true },
// Node {
// name: 'a',
// cost: 5,
// parents: Node { name: 'b', cost: 2, parents: [Object], processd: true },
// processd: true },
// Node {
// name: 'fin',
// cost: 6,
// parents: Node { name: 'a', cost: 5, parents: [Object], processd: true },
// processd: true } ]
ナップサック問題
決められた縛りの中で価値を最大化する問題。
重み1,価値1500 、 重み4,価値3000 、 重み3,価値2000
の品物がある。重さ4まで耐えれるナップサックに品物を入れていく。価値の最大値はいくつになるか
const MaxWeight = 4;
const Products = [
{
weight: 1,
value: 1500
},
{
weight: 4,
value: 3000
},
{
weight: 3,
value: 2000
},
];
const dpTable = {};
const dp = () => {
// 「前の最大値」の初期値を用意
for (let w = 1; w <= MaxWeight; w++) {
if (!dpTable[0]) {
dpTable[0] = {};
}
dpTable[0][w] = 0;
}
Products.forEach((product, index) => {
const productId = index + 1;
dpTable[productId] = {};
for (let weight = 1; weight <= MaxWeight; weight++) {
// 前の最大値
const prevMaxValue = dpTable[productId - 1][weight];
// 現在の品物の価値(現在の重みより軽ければ加算)
const curProductValue = (product.weight <= weight) ? product.value : 0;
// 残りのスペースの価値(現在の重み - 品物の重さ の位置のデータを取ってくる。負の値になった場合は 0 を入れる)
const maxValOfRemainingSpace = (dpTable[productId - 1][weight - product.weight] || 0);
// 現在の品物の価値 + 残りのスペースの価値
const curMaxValue = curProductValue + maxValOfRemainingSpace;
// 前の最大値 と (現在の品物の価値 + 残りのスペースの価値) を比較し、大きい方がその時の最適解
dpTable[productId][weight] = Math.max(prevMaxValue, curMaxValue);
}
});
return dpTable;
}
const result = dp();
console.log(result);
// { '0': { '1': 0, '2': 0, '3': 0, '4': 0 },
// '1': { '1': 1500, '2': 1500, '3': 1500, '4': 1500 },
// '2': { '1': 1500, '2': 1500, '3': 1500, '4': 3000 },
// '3': { '1': 1500, '2': 1500, '3': 2000, '4': 3500 } }
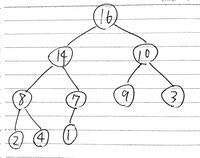
最大ヒープ
親より子供の方が値が小さい完全二分木。
配列で二分木を表した時に、親の配列のindexの値を i とするなら、左の子は 2*i 、右の子は 2*i+1 となる。
最大ヒープは真ん中の値(親)が左右の子供より必ず大きくなるので、親、左の子、右の子の中で最大のものを新しい親とする処理を行なっていく。
真ん中が最大値となったら部分木の根を移動して再度同じ処理を行なっていく。最終的に二分木全体の根で処理を行ったら完成。
親、左の子、右の子の中で最小のものを選ぶようにすれば、最小ヒープになる。
// 配列のindexに使っている値は二分木の位置。二分木の位置は1から始まっているので配列のindexを指定する際、常に-1を指定
const swap = (arr: number[], index: number, index2: number) => {
const tmp = arr[index - 1]
arr[index - 1] = arr[index2 - 1]
arr[index2 - 1] = tmp
}
const heap = (heapSize: number, arr: number[], cur: number) => {
const left = 2 * cur
const right = 2 * cur + 1
let max
if (left <= heapSize && arr[left - 1] > arr[cur - 1]) {
max = left
} else {
max = cur
}
if (right <= heapSize && arr[right - 1] > arr[max - 1]) {
max = right
}
if (max != cur) {
swap(arr, cur, max)
heap(heapSize, arr, max)
}
}
const buildMaxHeap = (arr: number[]) => {
const heapSize = arr.length
// 二分木では、配列の後半indexはリーフノードとなり、子ノードがぶら下がってないノードになる。
// heapの処理は親ノードと小ノードの大小を比較し、子の方が大きければswapする処理なので、リーフノードに対してheap処理をする必要はない。
// なので、配列の前半indexだけをheapの処理にかける
for (let cur = heapSize / 2; cur >= 1; cur--) {
heap(heapSize, arr, cur)
}
return arr
}
buildMaxHeap([4, 1, 3, 2, 16, 9, 10, 14, 8, 7]) // [ 16, 14, 10, 8, 7, 9, 3, 2, 4, 1 ]
ヒープソート
上述の最大ヒープを用いたソート。
この例では、最大ヒープ構造の配列の先頭要素をソート済み配列の生成に用いるので、降順でのソートになる。
最小ヒープを用いれば、昇順でのソートができる。
処理の流れのイメージは以下。コードの該当部分にもこのフローの番号をコメントで記載している。
- 引数で渡された配列で最大ヒープを作成
- 配列の先頭と末尾の要素を交換
最大ヒープなので、配列の先頭は配列内での最大値 - 末尾の要素を配列から取得し、ソート済み配列にpushする
2 で末尾の要素は配列内の最大値になってる。ソート済み配列には降順にデータがpushされていく。 - 先頭の要素に対して再度最大ヒープを作成
2 によりヒープの構造が崩れているので、ヒープの構造が満たされるように整頓しておく - 2 に戻る。これを引数で渡された配列の要素分、繰り返す。
参考: https://medium.com/@yasufumy/data-structure-heap-ecfd0989e5be
const heap = (heapSize: number, arr: number[], cur: number) => {
const left = 2 * cur
const right = 2 * cur + 1
let max
if (left <= heapSize && arr[left - 1] > arr[cur - 1]) {
max = left
} else {
max = cur
}
if (right <= heapSize && arr[right - 1] > arr[max - 1]) {
max = right
}
if (max != cur) {
const tmp = arr[cur - 1]
arr[cur - 1] = arr[max - 1]
arr[max - 1] = tmp
heap(heapSize, arr, max)
}
}
const buildMaxHeap = (arr: number[]) => {
const heapSize = arr.length
for (let cur = heapSize / 2; cur >= 1; cur--) {
heap(heapSize, arr, cur)
}
return arr
}
const heapSort = (arr: number[]) => {
const arrCopy = arr.slice()
buildMaxHeap(arr) // 1
const sortedArr: number[] = []
for (let i = 0; i < arrCopy.length; i++) {
const tmp = arr[0] // 2
arr[0] = arr[arr.length - 1]
arr[arr.length - 1] = tmp
sortedArr.push(arr.pop() as number) // 3
heap(arrCopy.length, arr, 1) // 4
}
return sortedArr
}
heapSort([4, 1, 3, 2, 16, 9, 10, 14, 8, 7]) // [16, 14, 10, 9, 8, 7, 4, 3, 2, 1]