毎回忘れては調べるので備忘録もかねて
取り上げている内容は以下です。
- 多クラス分類(CategoricalCrossentropy)
- 2値分類(BinaryCrossentropy)
- 回帰(MeanSquaredError)
共通問題とimport
モデルは適当に0~10の入力を取り、5以上なら1、5以下なら0を当てるモデルです。
import numpy as np
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras import layers as kl
from sklearn.metrics import accuracy_score
from matplotlib import pyplot as plt
# 値が5以上なら1、5以下なら0のデータ
x_train = np.random.uniform(0.0, 10.0, 1000)
y_train = np.where(x_train < 0.5, 0, 1)
多クラス分類(CategoricalCrossentropy)
多クラス分類は複数のクラスから1つの分類を当てる問題を想定します。
loss関数の数式は以下です。
$$H(p,q) = - \sum_x p(x) \log q(x)$$
各クラスの属する確率を最大化する問題と見て解きます。
出力層はsoftmaxになり、各値が0~1の値をとり合計すると1になります。
ですので、各クラスに属する確率が出力されるイメージになります。
CATEGORY_NUM = 2 # カテゴリ数(2は2値分類)
# 入力層と中間層(中間層は適当)
model = keras.Sequential()
model.add(kl.Input(shape=(1,)))
model.add(kl.Dense(64, activation="relu"))
model.add(kl.Dense(64, activation="relu"))
# 出力層
model.add(kl.Dense(CATEGORY_NUM, activation="softmax"))
# loss = "categorical_crossentropy" でも可
loss = tf.keras.losses.CategoricalCrossentropy()
model.compile(optimizer="adam", loss=loss)
loss をべた書きすると以下です。
def categorycal_cross_entropy(y_val, y_pred):
# int型だとエラーになりました
y_val = tf.cast(y_val, tf.float32)
y_pred = tf.cast(y_pred, tf.float32)
y_pred = tf.clip_by_value(y_pred, 1e-6, y_pred) # log(0)回避用
# -Σ p * log(q)
loss = -tf.reduce_sum(y_val * tf.math.log(y_pred), axis=1)
return tf.reduce_mean(loss)
正解ラベルとしてはone-hotエンコーディングされた形式を想定しています。
# one-hotエンコーディング
y_train_onehot = tf.one_hot(y_train, CATEGORY_NUM)
# y_train は[0,1, ... ,1] と0か1が入っている shape=(1000,)
# 返還後は[[1, 0], [0, 1], ... , [0, 1]] の形式 shape=(1000,2)
# 学習と予測
model.fit(x_train, y_train_onehot, epochs=10, batch_size=16)
y_pred = model(x_train).numpy()
# 評価(出力が各クラスの確率なので最大値を採用)
y_pred = np.argmax(y_pred, axis=1)
print(accuracy_score(y_pred, y_train)) # 1.0
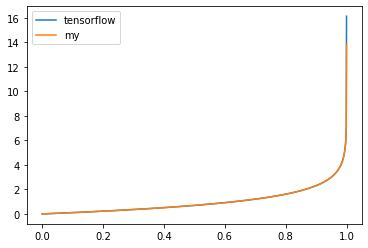
CategoricalCrossentropyを可視化してみました。
正解を[0, 1]とし、予測を[0, 1]~[1, 0]に変動させた結果をグラフにしています。
(x軸は左側の値)
loss = tf.keras.losses.CategoricalCrossentropy()
arr_x = []
arr_y1 = []
arr_y2 = [] # 確認用にべた書き版も
for x in np.linspace(0, 1, 1000):
arr_x.append(x)
x1 = np.array([[0.0, 1.0]]) # 正解
x2 = np.array([[x, 1-x]])
arr_y1.append(loss(x1, x2).numpy())
arr_y2.append(categorycal_cross_entropy(x1, x2).numpy())
plt.plot(arr_x, arr_y1, label="tensorflow")
plt.plot(arr_x, arr_y2, label="my")
plt.legend()
plt.show()
確率の誤差が0~0.8ぐらいまでは2以下でゆっくり上がりますが、それ以上離れると急激に増えますね。
(予測の差が広がると急激に誤差が広がる形です)
2値分類(BinaryCrossentropy)
多クラス分類の特殊な形です。
2値分類の場合は1から値を引くことで両方の確率を計算できるのでそれを使います。
loss関数の数式は、多クラス分類で使った交差エントロピーを展開した形になります。
$$H(p,q) = - (p \log(q) + (1-p) \log(1-q))$$
出力層はsigmoidになり、0~1の値をとります。
なのでそのまま確率が出力されるイメージです。
# 入力層と中間層(中間層は適当)
model = keras.Sequential()
model.add(kl.Input(shape=(1,)))
model.add(kl.Dense(64, activation="relu"))
model.add(kl.Dense(64, activation="relu"))
# 出力層
model.add(kl.Dense(1, activation="sigmoid"))
# loss = "binary_crossentropy" でも可
loss = tf.keras.losses.BinaryCrossentropy()
model.compile(optimizer="adam", loss=loss)
loss をべた書きすると以下です。
def binary_cross_entropy(y_val, y_pred):
# int型だとエラーになりました
y_val = tf.cast(y_val, tf.float32)
y_pred = tf.cast(y_pred, tf.float32)
y_pred = tf.clip_by_value(y_pred, 1e-6, 1-1e-6) # log(0)log(1)回避用
# - (p log(q) + (1-p) log(1-q))
loss = - (y_val * tf.math.log(y_pred) + (1-y_val) * tf.math.log(1 - y_pred))
return tf.reduce_mean(loss)
# 学習と予測
model.fit(x_train, y_train_onehot, epochs=10, batch_size=16)
y_pred = model(x_train).numpy()
# 評価(出力は0~1(確率)なので閾値0.5で変換)
y_pred = np.where(y_pred < 0.5, 0, 1)
print(accuracy_score(y_pred, y_train)) # 0.999
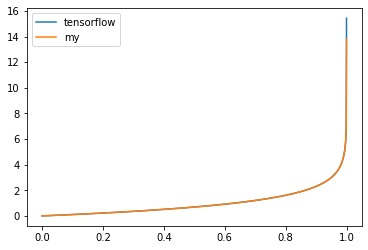
BinaryCrossentropyを可視化してみました。
正解を0とし、予測を0~1に変動させた結果をグラフにしています。
loss = tf.keras.losses.BinaryCrossentropy()
arr_x = []
arr_y1 = []
arr_y2 = [] # 確認用にべた書き版も
for x in np.linspace(0, 1, 1000):
arr_x.append(x)
x1 = np.array([0.0]) # 正解
x2 = np.array([x])
arr_y1.append(loss(x1, x2).numpy())
arr_y2.append(binary_cross_entropy(x1, x2).numpy())
plt.plot(arr_x, arr_y1, label="tensorflow")
plt.plot(arr_x, arr_y2, label="my")
plt.legend()
plt.show()
多クラス分類と同じ結果です。
回帰(MeanSquaredError)
回帰は分類ではなく数値を予測するタスクです。
今回はタスク自体は重要ではないので確率をそのまま数値として予測します。
loss関数は平均二乗誤差で、数式は以下です。
$$MSE(y, \hat{y}) = \frac{1}{n} \sum_{i=0}^{n-1} (y_i - \hat{y_i})^2$$
参考:https://ja.wikipedia.org/wiki/%E5%B9%B3%E5%9D%87%E4%BA%8C%E4%B9%97%E5%81%8F%E5%B7%AE
また、必ずしも平均二乗誤差を使う必要はなくタスクに合わせて変えても問題ありません。
(例えば差に二乗ではなく絶対値を使う平均絶対誤差などがあります)
出力層はlinear(線形)です。
要するにそのまま値が出力されます。
# 入力層と中間層(中間層は適当)
model = keras.Sequential()
model.add(kl.Input(shape=(1,)))
model.add(kl.Dense(64, activation="relu"))
model.add(kl.Dense(64, activation="relu"))
# 出力層(activationを省略した場合もlinearになります)
model.add(kl.Dense(1, activation="linear"))
# loss = "mse" でも可
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer="adam", loss=loss)
loss をべた書きすると以下です。
def mse(y_val, y_pred):
# 1/n Σ(y1 - y2)^2
loss = tf.reduce_mean(tf.square(y_val - y_pred))
return loss
# 学習と予測
model.fit(x_train, y_train_onehot, epochs=10, batch_size=16)
y_pred = model(x_train).numpy()
# 評価(出力は数値なので閾値0.5で変換)
y_pred = np.where(y_pred < 0.5, 0, 1)
print(accuracy_score(y_pred, y_train)) # 0.999
注意点としてはそのまま数値が出力されるのでマイナスの値や1以上の値も出力されます。
(まあ確率問題を回帰で求めることは特殊な場合じゃない限りしないと思いますが…)
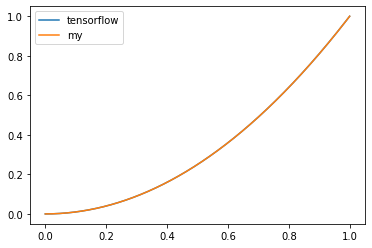
可視化すると以下です。
正解を0とし、予測を0~1に変動させた結果をグラフにしています。
loss = tf.keras.losses.MeanSquaredError()
arr_x = []
arr_y1 = []
arr_y2 = [] # 確認用にべた書き版も
for x in np.linspace(0, 1, 1000):
arr_x.append(x)
x1 = np.array([0.0]) # 正解
x2 = np.array([x])
arr_y1.append(loss(x1, x2).numpy())
arr_y2.append(mse(x1, x2).numpy())
plt.plot(arr_x, arr_y1, label="tensorflow")
plt.plot(arr_x, arr_y2, label="my")
plt.legend()
plt.show()
差の二乗が誤差になるので1以下だと差があまりないですね。
ただ二乗なので差が広がると急激に誤差が広がります。
おわりに
解きたいタスクが決まれば出力層と活性化関数はある程度決まると思いますが、案外まとめられているサイトを見つけられなかった印象です。
本当はマニアックなところまで書こうと思っていましたがそもそも知識がありませんでした。
有名どころだけになってしまいましたね…。
誰かの参考になれば幸いです。