拡散モデル入門②、SDE/ODEに基づくスコアベースの生成モデル（Tensorflow実装付き）

入門①：DDPMの理論とMNISTの実装
入門②：ここ
入門③：未定

SDE/ODEに基づくスコアベースの生成モデル

いろいろと検索して以下ブログに行きつきました。（有名な人のブログ？）

Score-based Generative Models based on SDEs/ODEs

かなり分かりやすく重要な内容だったので勉強がてら日本語に翻訳した記事となります。
翻訳と言っていますが、私が理解できるように言い回しを変えている箇所がある点は注意してください。

ちなみにSDEは確率微分方程式の事でODEは常微分方程式の事となります。

以下、ブログの内容です。

拡散ベースモデルの復習

拡散ベースモデル（diffusion-based models; 入門①のDDPMベースみたいなモデルの事）は1つ前の層に対して、ガウスノイズの追加による線形変換で構築されたモデルでした。
これは特殊な変分事後分布（Variational Posteriors）を持つ階層型VAE（Hierarchical VAEs）の表現と見ることができます。
また、これは離散化された時間を持つ動的なシステムと見ることもできます。

それを確認してみましょう。

まずデータポイント $x_0, x_0 \sim p_0(x) \equiv p_{\text{data}}(x)$ を既知の分布 $\pi, x_1 \sim p_1(x) \equiv \pi(x)$ からサンプリングされたノイズ $x_1$ に変換する事を考えます。
時間は $t \in [0,1]$ で表し、$x_0$ と $x_1$ の間には $T$ ステップあり、各ステップのサイズは $\Delta = \frac{1}{T}$ です。
この場合、順方向の拡散は以下です。

$$x_{t+\Delta} = \sqrt{1-\beta_t} x_t + \sqrt{\beta_t} \epsilon_t$$

ここで、$\epsilon_t \sim \mathcal{N}(0, I)$（ガウスノイズ）で、$\beta$はノイズの強度です。
これは時間を持つ動的なシステムとなり、後でまた触れます。

拡散ベースモデルの興味深い特徴として、線形性とガウス性によりデータ$x_0$から$x_1$を次のように直接計算できる事です。

$$x_{t} = \sqrt{\alpha_t} x_0 + \sqrt{1-\alpha_t} \epsilon_t$$

ここで、$\alpha_t = \prod_{\tau=1}^{t} (1 - \beta_{\tau})$です。
更にデータポイントを次のように計算できます。

$$x_{0} = \frac{1}{\sqrt{\alpha_t}} x_t - \frac{\sqrt{1-\alpha_t}}{\sqrt{\alpha_t}} \epsilon_t$$

ここでノイズ$\epsilon_t$は$t_1$から$t_0$に反転しているので、サンプリングした順方向とは違いノイズにアクセスできなくなります。
これに対する一般的な解決策は以下です。

ノイズを予測するネットワーク $\epsilon_{\theta}(x_t,t)$ の導入を考えます。
まず$x_t$について順方向の拡散を進めデータを得ます。
この時、それ以前の$x$やノイズ$\epsilon$を考慮しないとします。
それでもノイズ予測ネットワークは導入できます。

このネットワークの学習ですが、論文(Ho et al., 2020)¹では以下の損失で計算されます。

$$L_t(\theta) = |\epsilon_{\theta}(x_t, t) - \epsilon_t|^2$$

これはELBOと同じことが示されました。
しかしよく考えてみると別の損失と同じことが分かります。
それは別の記事に投稿したスコアマッチングの損失です。
標準偏差 $\sigma$ のガウスノイズ除去分布の場合、コアモデル(core model)とノイズモデルの間には次の対応関係があります。

$$s_\theta(x,t) = -\frac{\epsilon_{\theta}(x_t, t)}{\sigma}$$

まとめると以下です。

• 順方向の拡散は離散時間の動的システム
• 拡散ベースモデルの損失関数はスコアマッチング損失と（ほぼ）同じ
• 実際、拡散ベースモデルはスコアモデルに対応する
• 拡散ベースモデルは $\sigma$ のスケジュールでトレーニングされたスコアモデルと非常に似ており、どちらのモデルも反復的で、各ステップでより多くのノイズを考慮する。

これらの類似点はスコアモデルと拡散ベースモデルをより一般化できる可能性を示しています。

深層生成モデルとSDE/ODE

最初に戻りますが、拡散ベースモデルは離散時間を持つ動的システムと見なすことができます。
動的システムに関して入る前に微分方程式の世界を少し復習しておきます。
もっとしっかり学習したい方はこの本(Särkkä & Solin, 2019)²がお勧めです。

また、最新の研究ではSDE/ODEが生成モデルに多くのメリットをもたらすことが分かっているのでここで復習しておきます。

ODE（常微分方程式; Ordinary Differential Equation）

常微分方程式は確率を含まない、決定論的なシステムを記述する微分方程式となります。
一般的には以下です。

$$\frac{dx_t}{dt} = f(x_t,t)$$

初期条件 $x_0$ があり、$f(x_t,t)$はベクトル場とも呼ばれ時間の変化を表現する関数です。
ODEは時間を特定の間隔で離散化し、離散化した時間に対して数値計算法（numerical methods）を用いる事で解くことができます。

数値計算法とは、近似的に解を求める手法で、解析的に解けない場合や、解が複雑すぎる場合に使われます。

例としてオイラー法（Euler's method）では次のように実行されます。（$t=0$から開始し、ステップ$\Delta$で$t=1$進みます）

\begin{align}
x_{t+\Delta} - x_t &= f(x_t, t) \cdot \Delta \\
x_{t+\Delta} &= x_t + f(x_t, t) \cdot \Delta \\
\end{align}

$t=1$から$t=0$まで実行する場合は後退オイラー法（backward Euler's method）が適用できます。

$$x_t = x_{t+\Delta} - f(x_{t+\Delta}, t+\Delta) \cdot \Delta$$

生成モデルとの関連性が見えてきたでしょうか。
$x_0$をデータ、$x_1$をノイズとすると、$f(x_t,t)$が分かれば後退オイラー法を実行して生成モデルを得ることができます。

SDE（確率微分方程式; Stochastic Differential Equations）

次にSDEですが、一般的にSDEは軌跡がランダムなODEと考えることができ、各時点 $t$ においてある確率分布$p_t(x)$に従って分布するODEと考えることができます。
SDEは次のように定義されます。

$$dx_t = f(x_t, t) dt + g(t) d v_t$$

ここで $v$ は標準的なウィーナー過程（Wiener process）、$f(\cdot,t)$ はドリフト（drift）、$g(\cdot)$ は拡散（diffusion）と呼ばれるスカラー関数です。
ドリフト成分は決定論的です。（上記ODEより）
拡散は標準的なウィーナー過程により確率的になります。
ここではウィーナー過程についてはガウス分布のように振る舞うこと以上のことを知る必要はありません。
（例えば増加分の差は正規分布 $v_{t+\Delta} - v_t \sim \mathcal{N}(0, \Delta)$ になります）
（ウィーナー過程については(Särkkä & Solin, 2019)²を参照）

補足：ドリフトと拡散の形式は既知であると想定します

このSDEの重要な特性として、SDEに対応するODEが存在し、そのODEの解はSDEの解と同じ確率分布に従うという性質があることです。
データポイント $x_0$ から始める次の Probability Flow (PF) ODE³ を解くことでノイズ $x_1 \sim p_1(x)$ を得ることができます。

$$\frac{dx_t}{dt} = \left( f(x_t, t) - \frac{1}{2} g^2(t) \nabla_{x_t} \ln p_t(x_t) \right)$$

この式からわかることは以下です。

• ウィーナー過程はもうありません。その結果SDEではなくODEを扱うことになります。
• ドリフト成分と拡散成分はありますが、拡散成分は $-\frac{1}{2}$されて2乗されています。
• スコア関数 $\nabla_{x_t} \ln p_t(x_t)$ があります。（導出は論文³を参照）

これは妥当に見えます。
SDEには、$p_t(x)$ に従って分布する解があるため、スコア関数がここにあるのは驚くことではありません。
結局のところ、スコア関数は、$p_t(x)$ に従って軌跡がどのように見えるかを示します。

スコアベース生成モデルとPF-ODE

PF-ODEは、もしスコア関数が既知と仮定すると、$x_1 \sim \pi(x)$から始まる後退オイラー法を適用して生成モデルとして使用できます。

$$
x_t = x_{t+\Delta} - \left( f(x_{t+\Delta}, t+\Delta) - \frac{1}{2} g^2(t+\Delta) \nabla_{x_{t+\Delta}} \ln p_t(x_{t+\Delta}) \right) \cdot \Delta
$$

Perfect!
後問題はスコア関数ですが、スコア関数の学習にはノイズ除去スコアマッチングを使用できます。
（ノイズ除去スコアマッチングとは、ノイズ入りデータ分布を、各データ点を中心としたガウス分布の混合物であると考え、これを用いてスコアマッチングを行う手法）
ノイズ除去スコアマッチングとの違いは時間 $t$ を考慮する必要がある事です。

$$
L(\theta) = \int_0^1 L_t(\theta) dt
$$

$L_t(\theta)$ はどうやって定義しますか？
スコアマッチングでは $\lambda_t | s_\theta(x_t, t) - \nabla_{x_t} \ln p_t(x_t) |^2$ ですが、$p_t(x_t)$ が計算できないので他の方法を考えます。
代わりにデータポイント $x_0$ のノイズのあるバージョンをサンプリングできる分布 $p_{0t}(x_t|x_0)$ を定義します。
まとめると以下です。

L_t(\theta) = \frac{1}{2} \mathbb{E}_{x_0 \sim p_{\text{data}}(x)} \mathbb{E}_{x_t \sim p_{0t}(x_t | x_0)} \left[ \lambda_t \| s_\theta(x_t, t) - \nabla_{x_t} \ln p_{0t}(x_t | x_0) \|^2 \right]

重要なのは $p_{0t}(x_t|x_0)$ をガウス分布とするとスコア関数を解析的に計算できる点です。

計算例を見てみましょう。
$L_t(\theta)$ の計算は1つのサンプルから計算できます。（つまり、モンテカルロ推定（Monte Carlo estimate）ができます）
$s_{\theta}(x_t,t)$ を元に次のように後退オイラー法を実行してデータをサンプリングします。

$$
x_t = x_{t+\Delta} - \left( f(x_{t+\Delta}, t+\Delta) - \frac{1}{2} g^2(t+\Delta) s_\theta(x_{t+\Delta}, t+\Delta) \right) \cdot \Delta
$$

ドリフトと拡散が既知である事を想定していることに注意してください。
さらにここでは（後退）オイラー法に従っていますが、別のODEソルバーを適用しても問題ありません。
ここではできる限り明確かつシンプルにしたと考えています。

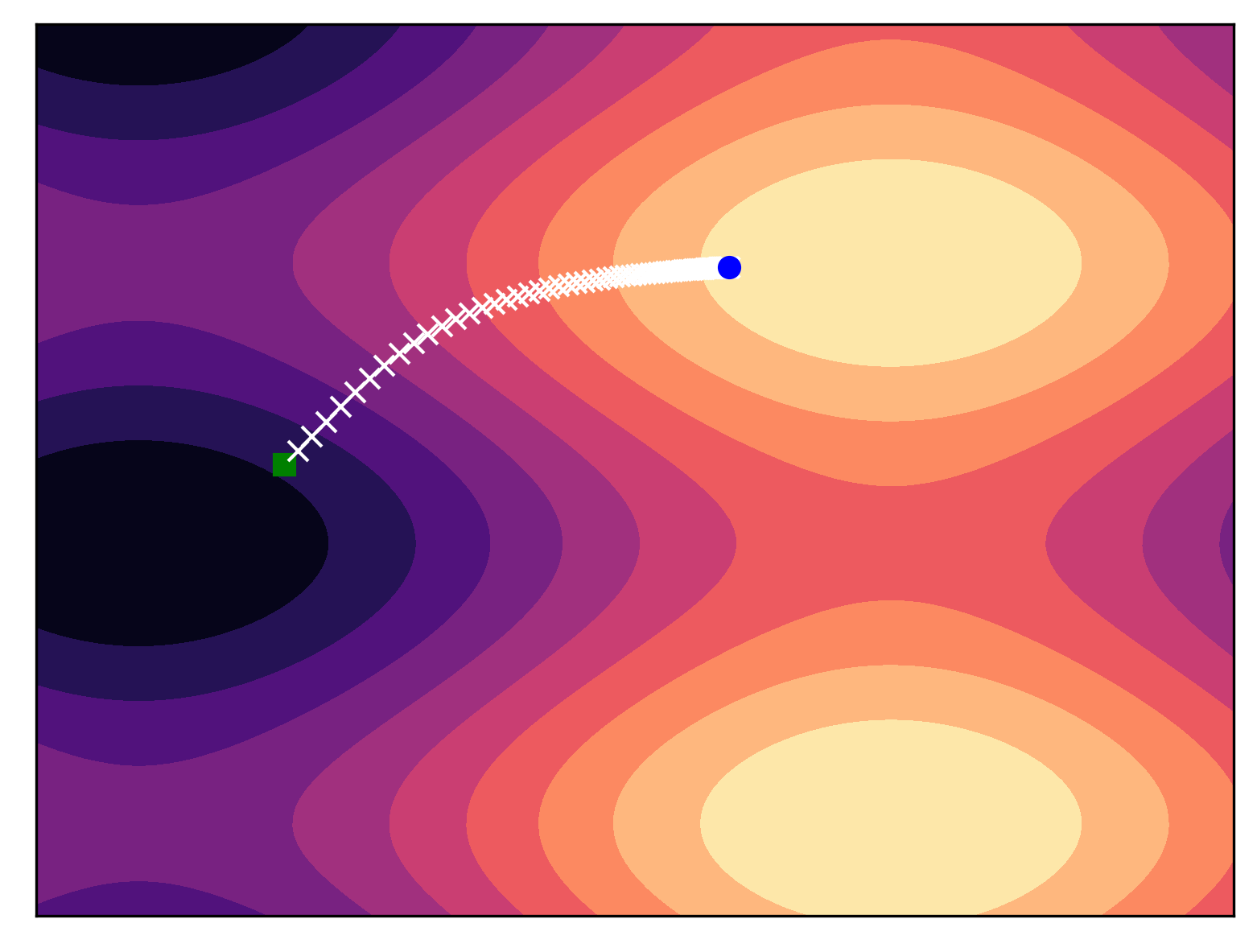
以下の図は多峰性分布に対して後退オイラー法でサンプリングした例です。
$f(x,t)=0$、$g(t)=9t$、$T=100$にて、スコア関数(モデルではありません)を自動微分で計算しました。

緑の四角が $x_1 \sim \pi$、青の円は $x_0$ です。
予想通りODEソルバーはモード（青の円）に向かって進みました。

この単純な例で PF-ODE の定義が強力な生成ツールであることがわかります。
スコア関数が適切に近似されると、元の分布から簡単な方法でサンプリングできます。

スコアベースの生成モデルの例: Variance Exploding PF-ODE

モデルの定式化

独自のスコアベース生成モデル（score-based generative model; SBGM）を定義するには以下が必要です。

• ドリフト $f(x,t)$
• 拡散 $g(t)$
• $p_{0t}(x_t|x_0)$

(Song et al., 2020)³と(Song et al., 2021)⁴にはVariance Exploding (VE) SDE, Variance Preserving SDE, sub-VP SDE の3種類のSBGMの例がありますが、ここはVE SDEに焦点を当てます。

VE SDEでの定義は以下です。

• $f(x,t)=0$
• $g(t)=\sigma^t$

ここで$\sigma>0$はハイパーパラメータで、時間$t \in [0,1]$で累乗されます。
これらを PF-ODE の一般形に代入すると以下です。

$$
\frac{d x_t}{d t} = -\frac{1}{2} \sigma^{2t} \nabla_{x_t} \ln p_t(x_t)
$$

スコアモデルを学習するためには ノイズ入り $x_0$ を取得するための条件付分布を定義する必要があります。
幸いなことにSDEの理論には、$p_{0t}(x_t|x_0)$の計算方法が示されています。
最終的な結果は以下です。

$$
p_{0t}(x_t | x_0) = \mathcal{N}(x_t | x_0, \frac{1}{2 \ln \sigma} (\sigma^{2t} - 1) I)
$$

時間に伴う分散関数は以下です。

$$
\sigma_t^2 = \frac{1}{2 \ln \sigma} (\sigma^{2t} - 1)
$$

最終的に最後の分布 $p_{01}(x)$ は $\sigma$ が十分に大きい場合、次のガウス分布に近づきます。

\begin{align}
p_{01}(x) &= \int p_0(x_0) * \mathcal{N}(x | x_0, \frac{1}{2 \ln \sigma} (\sigma^2 - 1) I) \\
&\approx \mathcal{N}(x | 0, \frac{1}{2 \ln \sigma} (\sigma^2 - 1) I) \\
\end{align}

$p_{01}(x)$ を使用してノイズ$x_1$をサンプリングし、それをデータ$x_0$に戻す事で生成が完成します。

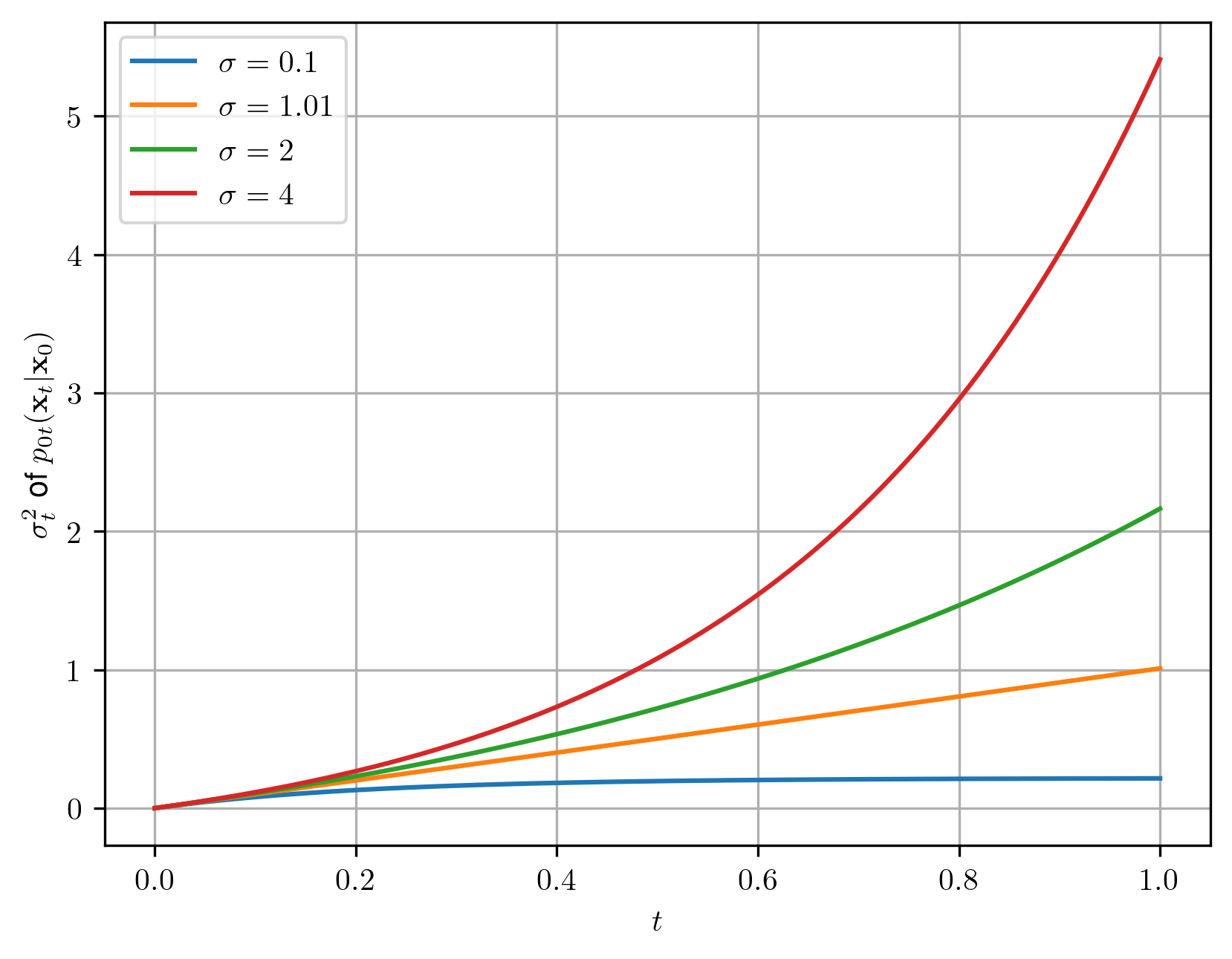
ハイパーパラメータ σ

$\sigma$ の値に対する $p_{0t}(x_t|x_0)$ の標準偏差への影響を見てみます。
まず $\sigma=1$ は選択できません。
なぜなら$ln(\sigma)$が0なので0で割ってしまうからです。
しかし$\sigma=1.01$ の場合、$p1(x)$ がほぼ標準ガウス分布になります。（t=1の場合を見て下さい）

ハイパーパラメータ λ

$L_{t}(\theta)$ にある $\lambda_r$ ですが、(Ho et al., 2020)¹では シンプルに $\lambda_t \equiv 1$ としていました。
しかしこれはそんなに簡単な話ではありません。
(Song et al., 2021)⁴ では VE PF-ODE の場合、$\lambda_t=\sigma^2_t$ に設定すると良い結果になる事を示しています。
また $L_{t}(\theta)$ は対数尤度関数の代用として使う事も出来、私たちはこれを学習の早期終了に利用しました。

SBDMの学習

手順は以下です。

1. データポイント $x_0$ を選択
2. ノイズをサンプリング、$x_1 \sim \pi(x) = \mathcal{N}(x | 0, I)$
3. 時間をサンプリング、$t \sim \text{Uniform}(0,1)$
4. $x_t = x_0 + \sqrt{\frac{1}{2 \ln \sigma}(\sigma^{2t} - 1)} \cdot x_1$（これは$p_{0t}(x_t|x_0)からのサンプルです$）
5. $x_t$と$t$からなるスコアモデル $s_{\theta}(x_t,t)$ を評価
6. スコアマッチング損失を計算。 $L_t(\theta) = \sigma_t^2 \left| x_1 - \sigma_t s_\theta(x_t, t) \right|^2$
7. 勾配法で $\theta$ を更新。 $\nabla_\theta L_t(\theta)$

この手順では意図的に $- \sigma_t s_\theta(x_t, t)$ を使っています。
$- \sigma_t s_\theta(x_t, t) = \epsilon_{\theta}(x_t,t)$ であり、$\sigma_t^2 \left| x_1 - \epsilon_{\theta}(x_t,t) \right|^2$ の拡散ベースのモデルに対応することになります。

サンプリング

最後に生成です。
VE PF-ODEは次の形式を取る後退オイラー法（または他のODEソルバー）を実行する事で生成になります。

\begin{align}
x_t &= x_{t+\Delta} + \left( \frac{1}{2} \sigma^{2(t + \Delta)} \left\{ -\frac{1}{\sigma^{t+\Delta}} s_\theta(x_{t+\Delta}, t+\Delta) \right\} \right) \cdot \Delta \\
&= x_{t+\Delta} - \left( \frac{1}{2} \sigma^{t+\Delta} s_\theta(x_{t+\Delta}, t+\Delta) \right) \cdot \Delta
\end{align}

以下から始めます。

$$
x_1 \sim p_{01}(x) = \mathcal{N}(x | 0, \frac{1}{2 \ln \sigma} (\sigma^2 - 1) I)
$$

Note: 最初の行にプラスがあるのは VE PF-ODEの拡散が $-\frac{1}{2} \sigma^{2t}$ なので、後退オイラー法のマイナスがプラスに代わるからです。これは明白かも知れませんがプラスとマイナスがごっちゃになるので明記しておきます。

実装のポイント

ブログでは残りは実際にコードを実装して動かした内容になっているのでポイントのみを書きます。

• データはスコアマッチングと同様に[-1,1]に変換
• VE-SBGMはノイズが多く、モデル化が難しい
• 20ステップの実行だが、通常は数百から数千のステップが必要
• 学習の早期終了が要検討、SBGMは収束速度がかなり遅いことが知られています
• SBGMは他にも様々なモデルが提案されています（元ブログ参照）
• SBGMの欠点の1つはサンプリング中のステップ数が多い事です。これを改善しT=10やT=5でよい優れたODEソルバーが発表されています。（元ブログ参照）
• その他の様々な改善方法について（元ブログ参照）
• SBGM の最新の概要については、この Web ページをご覧ください: link

ブログの内容は以上です。

実装

ここからはブログの翻訳ではなく私が実装してみた内容となります。
前回と同様MNIST+Tensorflowで実装しました。
入門①と同じ内容は省略します。（コード全体は最後にあります）

SBGM functions

時間に伴う分散関数

$$
\sigma_t^2 = \frac{1}{2 \ln \sigma} (\sigma^{2t} - 1)
$$

def sigma_function(t, sigma: float = 1.01):
    sigma_t = np.sqrt((1 / (2 * np.log(sigma)) * (sigma ** (2 * t) - 1)))
    return sigma_t.astype(np.float32)

時間tのサンプリング関数

0を含まない[0, 1]の範囲でランダムに取得しています。
TFとの兼ね合いで (batch_size, 1, 1, 1) にreshapeしています。

def sample_t(size: int, eps=1e-5):
    t = np.random.random(size).astype(np.float32)
    t = t * (1 - eps) + eps  # [0,1)->[eps,1)
    return t[..., np.newaxis, np.newaxis, np.newaxis]

x1のサンプリング関数

標準正規分布の乱数です。

$$x_1 \sim \pi(x) = \mathcal{N}(x | 0, I)$$

def sample_x1(shape):
    return np.random.normal(0, 1, size=shape).astype(np.float32)

xtの計算

$$
p_{0t}(x_t | x_0) = \mathcal{N}(x_t | x_0, \frac{1}{2 \ln \sigma} (\sigma^{2t} - 1) I)
$$

引数には元データ$x_0$、サンプリングされた$x_1$と$t$が入ります。

def calc_xt(x_0, x_1, t, sigma: float = 1.01):
    x_t = x_0 + sigma_function(t, sigma) * x_1
    return x_t

学習

学習箇所のみ抜粋です。

$$L_t(\theta) = \sigma_t^2 \left| x_1 - \sigma_t s_\theta(x_t, t) \right|^2$$

score_model = ニューラルネットワーク（今回はUNetを使用）

for 学習ループ:
    x_0 = データセットからバッチをサンプリング（元画像）

    # サンプリング
    t = sample_t(len(x_0))
    x_1 = sample_x1(x_0.shape)

    # xtを計算
    x_t = calc_xt(x_0, x_1, t)

    # その他学習に使う計算
    sigma_t = sigma_function(t)
    lambda_t = sigma_t**2

    # lossの計算
    with tf.GradientTape() as tape:
        x_pred = -sigma_t * score_model([x_t, t])
        loss = lambda_t * ((x_1 + x_pred) ** 2)
        loss = tf.reduce_mean(loss)
    grad = tape.gradient(loss, score_model.trainable_variables)
    optimizer.apply_gradients(zip(grad, score_model.trainable_variables))

生成

・初期データ

$$
x_1 \sim p_{01}(x) = \mathcal{N}(x | 0, \frac{1}{2 \ln \sigma} (\sigma^2 - 1) I)
$$

・ループ

x_t = x_{t+\Delta} - \left( \frac{1}{2} \sigma^{t+\Delta} s_\theta(x_{t+\Delta}, t+\Delta) \right) \cdot \Delta

size = 生成枚数
timesteps = 繰り返し回数
sigma = 1.01

# 初期データ
var = sigma_function(1, sigma) ** 2
x_t = np.random.normal(0, var, size=(size,) + img_shape).astype(np.float32)

# 各時間、1→0に生成
ts = np.linspace(1, eps, timesteps, dtype=np.float32)
delta_t = ts[0] - ts[1]
for t in ts[1:]:
    u = 0.5 * (sigma**t) * score_model([x_t, t])

    if False:
        # ブログはこっちだけどこれだと上手く生成できない
        x_t = x_t - u * delta_t
    else:
        # 本記事で変更箇所
        x_t = x_t - u * t
        if i != N - 2:
            r = tf.random.normal(x_t.shape)
            x_t += r * t

x_0 = x_t  # 生成データ

ブログ通りだと上手くいかなかったので少し変更しています。

学習結果

かなりナイーブな実装で精度は高くなかったので1のみを学習しました。

・ノイズ入り画像のサンプル

summaryの結果

Model: "u_net"
__________________________________________________________________________________________________
 Layer (type)                   Output Shape         Param #     Connected to
==================================================================================================
 input_2 (InputLayer)           [(None, 1, 1, 1)]    0           []

 dense (Dense)                  (None, 1, 1, 128)    256         ['input_2[0][0]']

 reshape (Reshape)              (None, 1, 1, 128)    0           ['dense[0][0]']

 input_1 (InputLayer)           [(None, 28, 28, 1)]  0           []

 up_sampling2d (UpSampling2D)   (None, 28, 28, 128)  0           ['reshape[0][0]']

 concatenate (Concatenate)      (None, 28, 28, 129)  0           ['input_1[0][0]',
                                                                  'up_sampling2d[0][0]']

 conv2d (Conv2D)                (None, 28, 28, 64)   74368       ['concatenate[0][0]']

 conv2d_1 (Conv2D)              (None, 28, 28, 64)   36928       ['conv2d[0][0]']

 max_pooling2d (MaxPooling2D)   (None, 14, 14, 64)   0           ['conv2d_1[0][0]']

 conv2d_2 (Conv2D)              (None, 14, 14, 128)  73856       ['max_pooling2d[0][0]']

 conv2d_3 (Conv2D)              (None, 14, 14, 128)  147584      ['conv2d_2[0][0]']

 max_pooling2d_1 (MaxPooling2D)  (None, 7, 7, 128)   0           ['conv2d_3[0][0]']

 conv2d_4 (Conv2D)              (None, 7, 7, 512)    590336      ['max_pooling2d_1[0][0]']

 up_sampling2d_1 (UpSampling2D)  (None, 14, 14, 512)  0          ['conv2d_4[0][0]']

 concatenate_1 (Concatenate)    (None, 14, 14, 640)  0           ['up_sampling2d_1[0][0]',
                                                                  'conv2d_3[0][0]']

 conv2d_5 (Conv2D)              (None, 14, 14, 128)  737408      ['concatenate_1[0][0]']

 conv2d_6 (Conv2D)              (None, 14, 14, 128)  147584      ['conv2d_5[0][0]']

 up_sampling2d_2 (UpSampling2D)  (None, 28, 28, 128)  0          ['conv2d_6[0][0]']

 concatenate_2 (Concatenate)    (None, 28, 28, 192)  0           ['up_sampling2d_2[0][0]',
                                                                  'conv2d_1[0][0]']

 conv2d_7 (Conv2D)              (None, 28, 28, 64)   110656      ['concatenate_2[0][0]']

 conv2d_8 (Conv2D)              (None, 28, 28, 64)   36928       ['conv2d_7[0][0]']

 conv2d_9 (Conv2D)              (None, 28, 28, 1)    65          ['conv2d_8[0][0]']

==================================================================================================
Total params: 1,955,969
Trainable params: 1,955,969
Non-trainable params: 0

学習過程

Epoch 1/10: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:06<00:00, 16.82it/s, loss=0.0805]
Epoch 2/10: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.36it/s, loss=0.0553] 
Epoch 3/10: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.27it/s, loss=0.0407] 
Epoch 4/10: 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.48it/s, loss=0.031] 
Epoch 5/10: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.29it/s, loss=0.0241] 
Epoch 6/10: 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.42it/s, loss=0.026] 
Epoch 7/10: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.33it/s, loss=0.0245] 
Epoch 8/10: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.30it/s, loss=0.0324] 
Epoch 9/10: 100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.37it/s, loss=0.0312] 
Epoch 10/10: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 106/106 [00:03<00:00, 27.29it/s, loss=0.0255] 

・生成結果

・生成過程

全体コード

学習結果

from pathlib import Path

import numpy as np
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow import keras
from tqdm import tqdm

kl = keras.layers


img_shape = (28, 28, 1)


def create_dataset():
    (x_train, y_train), (_, _) = keras.datasets.mnist.load_data()
    x_train = x_train[y_train == 1]
    x_train = (x_train[..., np.newaxis] / 255.0) * 2 - 1  # [0,255] -> [-1,1]
    x_train = x_train.astype(np.float32)
    return x_train


def decode_image(x):
    img = np.clip(x, -1.0, 1.0)
    # [-1,1] -> [0,255]
    img = (((img + 1) / 2) * 255).astype(np.uint8)
    return img


# ----------------------------------
# SBGM functions
# ----------------------------------
def sigma_function(t, sigma: float = 1.01):
    # 時間に伴う分散関数
    sigma_t = np.sqrt((1 / (2 * np.log(sigma)) * (sigma ** (2 * t) - 1)))
    return sigma_t.astype(np.float32)


def sample_t(size: int, eps=1e-5):
    t = np.random.random(size).astype(np.float32)
    t = t * (1 - eps) + eps  # [0,1)->[eps,1)
    return t[..., np.newaxis, np.newaxis, np.newaxis]


def sample_x1(shape):
    # ノイズをサンプリング
    x1 = np.random.normal(0, 1, size=shape).astype(np.float32)
    return x1


def calc_xt(x_0, x_1, t, sigma: float = 1.01):
    # p_0t(x_t|x_0) を計算
    x_t = x_0 + sigma_function(t, sigma) * x_1
    return x_t


def build_unet(img_shape: tuple[int, int, int]) -> keras.Model:
    # 入力はノイズ入り画像とタイムステップ
    x_t = kl.Input(shape=img_shape)
    t = keras.Input(shape=(1, 1, 1))

    # --- タイムステップ層
    # (1, 1, 1) -> (1, 1, dim) -> (28, 28, dim)
    t_embedding = kl.Dense(128, activation="gelu")(t)
    t_embedding = kl.Reshape((1, 1, 128))(t_embedding)
    t_embedding = kl.UpSampling2D(img_shape[:2])(t_embedding)

    # タイムステップ情報をチャンネルに追加
    x = kl.Concatenate()([x_t, t_embedding])

    # --- down sampling
    c1 = kl.Conv2D(64, (3, 3), padding="same", activation="relu")(x)
    c1 = kl.Conv2D(64, (3, 3), padding="same", activation="relu")(c1)
    p1 = kl.MaxPooling2D((2, 2))(c1)  # 28x28 -> 14x14
    c2 = kl.Conv2D(128, (3, 3), padding="same", activation="relu")(p1)
    c2 = kl.Conv2D(128, (3, 3), padding="same", activation="relu")(c2)
    p2 = kl.MaxPooling2D((2, 2))(c2)  # 14x14 -> 7x7

    # ---　ボトム
    p2 = kl.Conv2D(512, (3, 3), activation="relu", padding="same")(p2)

    # ---　up sampling
    u1 = kl.UpSampling2D((2, 2))(p2)  # 7x7 -> 14x14
    u1 = kl.Concatenate()([u1, c2])
    u1 = kl.Conv2D(128, (3, 3), activation="relu", padding="same")(u1)
    u1 = kl.Conv2D(128, (3, 3), activation="relu", padding="same")(u1)
    u2 = kl.UpSampling2D((2, 2))(u1)  # 14x14 -> 28x28
    u2 = kl.Concatenate()([u2, c1])
    u2 = kl.Conv2D(64, (3, 3), activation="relu", padding="same")(u2)
    u2 = kl.Conv2D(64, (3, 3), activation="relu", padding="same")(u2)

    y = kl.Conv2D(1, (1, 1), padding="same")(u2)

    model = keras.Model(inputs=[x_t, t], outputs=y, name="u_net")
    return model


class SGBM:
    def __init__(self, img_shape, sigma=1.01, eps=1e-5):
        self.sigma = sigma
        self.eps = eps

        # Score model
        self.model = build_unet(img_shape)
        self.optimizer = keras.optimizers.Adam(learning_rate=0.0005)

    def train(self, x_0):
        # timestepとガウスノイズをサンプリング
        t = sample_t(len(x_0), self.eps)
        x_1 = sample_x1(x_0.shape)

        # ノイズ入り画像を計算
        x_t = calc_xt(x_0, x_1, t, sigma=self.sigma)

        # loss計算用の変数
        sigma_t = sigma_function(t, sigma=self.sigma)
        lambda_t = np.sqrt(sigma_t)

        # LOSS: Score matching
        with tf.GradientTape() as tape:
            x_pred = -sigma_t * self.model([x_t, t])
            loss = lambda_t * ((x_1 + x_pred) ** 2)
            loss = tf.reduce_mean(loss)
        grad = tape.gradient(loss, self.model.trainable_variables)
        self.optimizer.apply_gradients(zip(grad, self.model.trainable_variables))

        return loss.numpy()

    def generate(self, size: int, N: int):
        var = sigma_function(1, self.sigma) ** 2
        x_t = np.random.normal(0, var, size=(size,) + img_shape).astype(np.float32)

        samples_history = []

        # オイラー法
        ts = np.linspace(1, self.eps, N, dtype=np.float32)
        delta_t = ts[0] - ts[1]
        x_t = tf.convert_to_tensor(x_t, dtype=tf.float32)  # np -> tf
        for i in tqdm(range(N - 1), desc="sampling loop"):
            t = ts[i + 1]
            t = np.tile(np.reshape(t, (1, 1, 1, 1)), (size, 1, 1, 1))

            u = 0.5 * (self.sigma**t) * self.model([x_t, t])
            if False:
                # ブログはこっちだけどこれだと上手く生成できない
                x_t = x_t - u * delta_t
            else:
                # 本記事で変更箇所
                x_t = x_t - u * t
                if i != N - 2:
                    r = tf.random.normal(x_t.shape)
                    x_t += r * t

            samples_history.append(x_t.numpy())

        return x_t, samples_history


# ----------------------------------
# main
# ----------------------------------
def sample():
    # --- σ
    t = np.linspace(0, 1, 100)
    for sigma in [0.1, 1.01, 2, 4]:
        var_t = sigma_function(t, sigma) ** 2
        plt.plot(t, var_t, label=rf"$\sigma={sigma}$")
    plt.xlabel("t")
    plt.ylabel(r"$\sigma^2_t$")
    plt.grid()
    plt.legend()
    plt.tight_layout()
    plt.show()

    # --- ノイズ入り画像作成
    imgs = create_dataset()
    t = np.array([0, 0.2, 0.4, 0.6, 0.8, 1])[..., np.newaxis, np.newaxis, np.newaxis]
    x_0 = imgs[: len(t)]
    noise = sample_x1(x_0.shape)
    x_t1 = calc_xt(x_0, noise, t, sigma=0.1)
    x_t2 = calc_xt(x_0, noise, t, sigma=1.01)
    x_t3 = calc_xt(x_0, noise, t, sigma=2)
    x_t4 = calc_xt(x_0, noise, t, sigma=4)

    def plot_sample(imgs, xlabels, ylabels):
        h = len(imgs)
        w = len(imgs[0])
        fig, axes = plt.subplots(h, w, figsize=(6, 6), sharex=True, sharey=True)
        for y in range(h):
            for x in range(w):
                axes[y, x].imshow(imgs[y][x], cmap="gray")
                axes[y, x].set_xticks([])
                axes[y, x].set_yticks([])
                axes[y, x].set(xlabel=xlabels[x], ylabel=ylabels[y])
                axes[y, x].label_outer()
        plt.tight_layout()
        plt.show()

    plot_sample(
        [
            decode_image(x_0),
            decode_image(noise),
            decode_image(x_t1),
            decode_image(x_t2),
            decode_image(x_t3),
            decode_image(x_t4),
        ],
        xlabels=[f"t={t[0][0][0]}" for t in t.tolist()],
        ylabels=["Original", "Noise", "σ=0.1", "σ=1.01", "σ=2", "σ=4"],
    )

    # --- Model
    model = build_unet(img_shape)
    model.summary()


def train(epochs: int = 10, batch_size: int = 64):
    x_train = create_dataset()
    sgbm = SGBM(img_shape)

    # 学習用にデータをバッチ化
    train_dataset = tf.data.Dataset.from_tensor_slices(x_train).shuffle(len(x_train)).batch(batch_size)

    for epoch in range(epochs):
        with tqdm(train_dataset, desc=f"Epoch {epoch + 1}/{epochs}") as pbar:
            for x_0 in pbar:
                loss = sgbm.train(x_0)
                pbar.set_postfix(loss=loss)  # 損失を進捗バーに表示
    sgbm.model.save_weights(Path(__file__).parent / "diff.weights.h5")


def generate(timesteps: int = 1000):
    sgbm = SGBM(img_shape)
    sgbm.model.load_weights(Path(__file__).parent / "diff.weights.h5")

    # 生成
    num_samples = 16
    samples, samples_history = sgbm.generate(num_samples, timesteps)

    samples = decode_image(samples)
    samples_history = decode_image(samples_history)

    # 結果
    plt.figure(figsize=(10, 10))
    for i in range(num_samples):
        plt.subplot(4, 4, i + 1)
        plt.imshow(samples[i, :, :, 0], cmap="gray")
        plt.axis("off")
    plt.show()

    # 作成過程
    index = 4
    img_list = np.array(samples_history)[:, index, :, :, 0]
    plt.figure(figsize=(20, 5))
    step_idxs = list(range(0, len(img_list), int(timesteps / 12)))  # 多いので一定間隔で抜き出し
    step_idxs += [len(img_list) - 1]  # 最後も追加
    for i, idx in enumerate(step_idxs):
        plt.subplot(1, len(step_idxs), i + 1)
        plt.imshow(img_list[idx], cmap="gray")
        plt.xticks([])
        plt.yticks([])
        plt.xlabel(f"step={idx}")
    plt.show()


if __name__ == "__main__":
    sample()
    train(epochs=10)
    generate(timesteps=1000)

最後に

ちゃんと理論背景まで解説する参考資料がほとんどなかったのですごく助かりました。
最初はうまく生成できませんでしたが少しいじったらちゃんと生成できました。
その３を調べてる影響もあったりします。

誰かの参考になれば幸いです。

1. (Ho et al., 2020) Ho, J., Jain, A. and Abbeel, P., 2020. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33, pp.6840-6851. ↩ ↩²

2. (Särkkä & Solin, 2019) Särkkä, S. and Solin, A., 2019. Applied stochastic differential equations (Vol. 10). Cambridge University Press. ↩ ↩²

3. (Song et al., 2020) Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2020). Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456. ↩ ↩² ↩³

4. (Song et al., 2021) Song, Y., Durkan, C., Murray, I. and Ermon, S., 2021. Maximum likelihood training of score-based diffusion models. Advances in Neural Information Processing Systems, 34, pp.1415-1428. ↩ ↩²