こんにちは、東北投信というブログサイトを運営している者です。今回は東北投信で「最小分散ポートフォリオ」を求めるJavascript製のツールを作ってみたので、作成などにまつわる話を書いてみます。
実物はこちら↓
最小分散ポートフォリオ算出ツール(βバージョン) by 東北投信
https://blog.tacos-heaven.xyz/tool/low_volatility_tool.html
作成にあたっては以下の記事を参考にさせていただきました。
Pythonで5資産の最適なアセットアロケーションを計算
https://qiita.com/an_orchid/items/05205cd3919bdaae16b0
最小分散ポートフォリオとは
株式市場全体を母集団として複数銘柄でのポートフォリオを組み、横軸にリスク、縦軸に期待リターンをとって同一リスクのポートフォリオのなかでリターンが最大となるポートフォリオを結んだ曲線(=効率的フロンティア)を描いた際、この曲線上でリスク(=分散)が最小となるポートフォリオが最小分散投資である。
最小分散投資(さいしょうぶんさんとうし)
https://www.nomura.co.jp/terms/japan/sa/A02356.html
この説明では株式を対象にしていますが、今回作ったのは8つの資産クラス(国内・先進国の株式・債券・REITと、新興国債券の株式・債券)の組み合わせから最小分散ポートフォリオを求めるツールです。いわゆる、つみたてNISAやiDeCoでインデックス投資でアセットアロケーションを組むことを前提に作っています。
ローリターンからハイリターンまでの様々な資産から最小分散ポートフォリオを求めると、必然的にリターンが最小化されてしまうため、今回は目標リターンを入力し、そのリターンを実現する範囲内でリスクを最小化するアセットアロケーションを求めました。
作成手順解説
処理の流れはそれほど難しくなく、
- 総当りの資産配分の組み合わせを作る
- 各組み合わせごとにリスクとリターンを算出し、最も運用効率が良くなるものを記録
- あとグーグルチャートを使って情報表示とか
と力技で求めています。どちらかといえば、資産配分を細かくするほど処理に時間がかかる点が問題になりました。
総当りの資産配分の組み合わせを作る
総当りの資産配分を作ります。配分は少しずつ変えてリスクとリターンを計算し、最良な結果を探し出しています。
筆者の環境で試したところでは、資産配分は10%刻みまでは許容範囲内ですが、5%刻みにすると分単位で時間がかかるようになるため、リリース版では10%(低速)と20%(高速)で選べるようにしました。実際のところ、効率的フロンティアは常に一定とは限らないので、計算の精度を高めてもあまり意味がありません。
なお、後述しますが、得られるアセットアロケーションは少々現実味がないことが多いので、敢えて特定の資産を計算から外せるように作っています。
// 資産配分は20%刻みとする
var stepValue = 5
// ある資産クラスを資産配分の計算に含めるか否かのスイッチ(8資産分用意する)
var checkJpnStock = false;
//最小分散ポートフォリオを記録する配列
var minimumVolatilityPortfolio = new Array(NUM_OF_ASSETS);
// 資産配分の比率を収める配列(8資産分用意する)
// 計算から外す場合にはゼロ%のデータだけ用意する
var potentialAllocJpnStock = new Array(stepValue);
for(let i = 0; i < stepValue; i++) {
potentialAllocJpnStock[i] = (checkJpnStock == true) ? 0 : a * stepValue / (Math.pow(stepValue, 2));
}
// 投資比率の刻みを決める。計算から外す場合は、処理速度向上のためゼロ%の場合のみ(1回だけ)考慮する
// 他の7つの資産も同じ計算を行なう
var loopJpnStock = (checkJpnStock == true) ? 1 : stepValue; // 日本株式
// 資産配分の組み合わせの分だけfor文を回す
for(let a = 0; a < loopJpnStock; a++) {
for(let b = 0; b < loopJpnBond; b++) {
for(let c = 0; c < loopJpnReit; c++) {
for(let d = 0; d < loopDevStock; d++) {
for(let e = 0; e < loopDevBond; e++) {
for(let f = 0; f < loopDevReit; f++) {
for(let g = 0; g < loopEmgStock; g++) {
for(let h = 0; h < loopEmgBond; h++) {
// このループの中で各資産配分の組み合わせでリスクとリターンを求める
// もっとも条件の良い計算結果を記録していく
}
}
}
}
}
}
}
}
リスクとリターンの算出
ループの中で算出するのは期待リターンとリスク(標準偏差)です。
リターンの算出
期待リターンの算出は簡単で、資産クラスのリターンとその資産クラスの占める比率を掛けた結果を全て合算して算出します。
// portfolioReturnは期待リターン
// assetRate[i]とassetReturn[i]には各資産クラスの比率とリターンが入ってる
var portfolioReturn = 0;
const NUM_OF_ASSETS = 8;
for(let i = 0; i < NUM_OF_ASSETS; i++) {
portfolioReturn = assetRate[i] * assetReturn[i] + portfolioReturn;
}
リスクの算出
リスクの計算は少しややこしいです。
// portfolioRiskは期待リスク(標準偏差)
// assetRate[i]とassetRisk[i]には各資産クラスの比率とリスクが入ってる
// coefficient[j][i]は資産クラス間の相関係数
var tmpriskA = 0;
var tmpriskB = 0;
// 下準備
for(let i = 0; i < NUM_OF_ASSETS; i++) {
tmpriskA = assetRate[i] * assetRate[i]* assetRisk[i] * assetRisk[i] + tmpriskA;
}
for(let j = 0; j < NUM_OF_ASSETS; j++) {
for(let i = j + 1; i < NUM_OF_ASSETS; i++) {
tmpriskB = assetRisk[i] * assetRate[i] * coefficient[j][i] * assetRisk[j] * assetRate[j] + tmpriskB;
}
}
// 分散から標準偏差に変換
portfolioRisk = Math.sqrt(tmpRiskA + (2 * tmpRiskB));
グーグルチャートで情報表示
求めた最小分散ポートフォリオはグーグルパイチャートを使って表示します。
Visualization: Pie Chart
https://developers.google.com/chart/interactive/docs/gallery/piechart
ほとんどテンプレコードのまま使っています。
// minimumVolatilityPortfolioに最小分散ポートフォリオを実現するアセットアロケーションが記録されている
// 円グラフ表示
google.load("visualization", "1", {packages:["corechart"]});
google.setOnLoadCallback(drawChart);
function drawChart() {
var data = google.visualization.arrayToDataTable([ //グラフデータの指定
['Asset', 'Ratio'],
['国内株式', minimumVolatilityPortfolio[0]],
['国内債券', minimumVolatilityPortfolio[1]],
['国内REIT', minimumVolatilityPortfolio[2]],
['先進国株式', minimumVolatilityPortfolio[3]],
['先進国債券', minimumVolatilityPortfolio[4]],
['先進国REIT', minimumVolatilityPortfolio[5]],
['新興国株式', minimumVolatilityPortfolio[6]],
['新興国債券', minimumVolatilityPortfolio[7]]
]);
var options = { //オプションの指定
title: 'アセットアロケーション',
titleTextStyle: {color:'#000', bold:true, fontSize:20},
chartArea: {left:15, width:windowsize}, // windowsizeはディスプレイの横サイズを入れた変数
pieHole: 0.4,
};
var chart = new google.visualization.PieChart(document.getElementById('piechart')); //グラフ表示させる要素の指定
chart.draw(data, options);
}
最小分散ポートフォリオで求めた結果は??
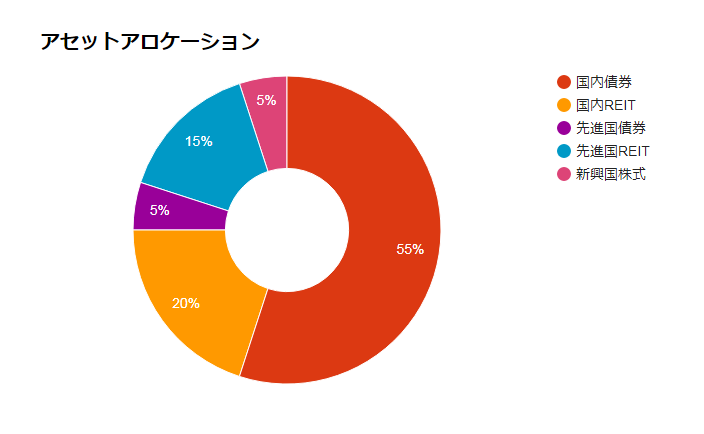
myINDEXの過去20年データとeMAXISの相関係数を用いて、利回り5%を実現する最小分散ポートフォリオを求めると
- 国内債券:55%
- 国内REIT:20%
- 先進国債券:5%
- 先進国REIT:15%
- 新興国株式:5%
という、「ちょっと変わった」配分になります。一般的には株式を中心にアセットアロケーションを組むことが多いので、日本株も先進国株も含めない配分は「異例」です。データとしてはそうなりますが、「他の人と配分が大きく違う」という点で選びにくいアセットアロケーションです。
myINDEXのデータとeMAXISの相関係数を使って求めた過去の最小分散ポートフォリオ。目標利回りは5%でリスクは6.78%
— みらい@招財進寶 (@instockexnet) 2019年3月26日
なぜかREITの主張が強いです
なお、メインの運用とは別に最小分散ポートフォリオと同じ配分で投信を買ってみようかと画策中 pic.twitter.com/SCxKWtraIE
個別株ならともかく、インデックスファンドを用いた投資は20年や30年といった長期間継続するのが有効とされています。また、現在の非課税制度(つみたてNISA)は、インデックスファンドの頻繁な売買には向いていない特徴も持っています(iDeCoなら非課税スイッチングOK)。
故に、インデックス投資において、ある時点の最小分散ポートフォリオを求めるメリットは薄く、数字遊びの域を出ないかな、というのが本音です。
売買に制限のないロボアドあたりはやってるかもしれませんが、そこは筆者の知るところではありません。
参考
EXCELで学ぶファイナンス証券投資分析
https://www.amazon.co.jp/dp/432211394X
最小分散投資(さいしょうぶんさんとうし)
https://www.nomura.co.jp/terms/japan/sa/A02356.html
Pythonで5資産の最適なアセットアロケーションを計算
https://qiita.com/an_orchid/items/05205cd3919bdaae16b0
『myINDEX』 わたしのインデックス
https://myindex.jp/
(参考)各ファンドの相関係数
https://emaxis.jp/special/sokan.html