1. はじめに
1.1 何ができるか
5資産の最適なアセットアロケーションをもとめることができる。1資産の期待収益率(期待リターン)とボラティリティ(標準偏差、リスク)は既知のものとする。欲しい期待収益率をinputし、最適なアセットアロケーション(資産配分)をoutputする。ここで、最適なアセットアロケーションとは、効率的フロンティア曲線に乗るような資産の組み合わせのことと定義する。(もう少しわかりやすく言い換えると、「最適なアセットアロケーションを計算する」とは、「欲しい期待収益率を固定したときに標準偏差が最小となるような資産配分を求める」ということである。)
2. プログラミング
2.1 複数の資産の期待収益率の求め方
投資比率が均等のときは単純に平均すればいい。投資比率が異なる場合は、その重みを考慮すればいい。5資産から成るポートフォリオの期待収益率$r_p$は、資産$i$の期待収益率$r_i$、資産$i$の投資比率$x_i$のとき、以下のように表すことができる。
$$r_p=\sum_{i=1}^5 r_ix_i$$
プログラムにすると、以下のようになる。
rp=0
for i in range(0,5):
rp+=r[i]*x[i]
2.2 複数の資産の標準偏差の求め方
それぞれの資産の標準偏差がわかっていても、それが組み合わさったときの標準偏差は単純に平均すればいいわけではない。5資産から成るポートフォリオの標準偏差$\sigma_p$(⇔分散${\sigma_p}^2$)と、資産$i$と資産$j$の収益率の相関係数$\rho_{ij}$、資産$i$の収益率の標準偏差$\sigma_i$、資産$i$の投資比率$x_i$の関係は、以下のように表すことができる。[1]
$${\sigma_p}^2=\sum_{i=1}^5\sum_{j=1}^5\rho_{ij}\sigma_i\sigma_jx_ix_j$$
添え字については[2]。これをプログラムにすると、以下のようになる。
sigmap=0
for i in range(0,5):
for j in range(0,5):
sigmap+=rho[i][j]*sigma[i]*sigma[j]*x[i]*x[j]
2.3 投資比率の決定
2.3.1 手動で設定
$x$は投資比率であったから、合計すると100%にならなくてはならない。つまり、x[0]+x[1]+x[2]+x[3]+x[4]が100%になる組み合わせである必要がある。例えば、x[0]=50%, x[1]=0%, x[2]=20%, x[3]=20%, x[4]=10%とするとき、5資産の期待収益率と標準偏差は以下のように計算できる。
# -*- coding: utf-8 -*-
"""
5資産の期待収益率と標準偏差を計算
"""
import numpy as np
# -------------------------------------------------
# input data
# -------------------------------------------------
r = [1.00,4.80,3.50,5.00,9.25] # 期待収益率
rho = [[1,0.16,-0.06,-0.05,-0.29],
[0.16,1,-0.25,0.27,0.73],
[-0.06,-0.25,1,0.56,0.11],
[-0.05,0.27,0.56,1,0.91],
[-0.29,0.73,0.11,0.91,1]] # 相関係数
sigma=[5.4,22.15,13.25,19.59,26.25] # 標準偏差
x = [0.5,0,0.2,0.2,0.1] # 投資比率
# -------------------------------------------------
# 本文
# -------------------------------------------------
n=len(x) # 資産の数
# ----期待収益率----
rp=0
for i in range(0,n):
rp+=r[i]*x[i]
# ----標準偏差----
sigmap=0
for i in range(0,n):
for j in range(0,n):
sigmap+=rho[i][j]*sigma[i]*sigma[j]*x[i]*x[j]
sigmap=np.sqrt(sigmap) # 分散から標準偏差に変換
# ----output----
print('ポートフォリオの期待収益率 {:.2f}'.format(rp))
print('ポートフォリオの標準偏差 {:.2f}'.format(sigmap))
出力結果:ポートフォリオの期待収益率 3.12
ポートフォリオの標準偏差 7.90
ここで、資産の期待収益率と標準偏差、相関係数は以下の数字を用いた[3]。
| No | 資産クラス | 期待収益率 | 標準偏差 |
|---|---|---|---|
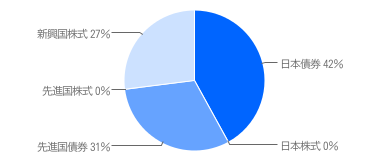
| 資産0 | 国内債券 | 1.00% | 5.40% |
| 資産1 | 日本株式 | 4.80% | 22.15% |
| 資産2 | 先進国債券 | 3.50% | 13.25% |
| 資産3 | 先進国株式 | 5.00% | 19.29% |
| 資産4 | 新興国株式 | 9.25% | 26.25% |
| 相関係数 | 資産0 | 資産1 | 資産2 | 資産3 | 資産4 |
|---|---|---|---|---|---|
| 資産0 | 1 | 0.16 | -0.06 | -0.05 | -0.29 |
| 資産1 | 0.16 | 1 | -0.25 | 0.27 | 0.73 |
| 資産2 | -0.06 | -0.25 | 1 | 0.56 | 0.11 |
| 資産3 | -0.05 | 0.27 | 0.56 | 1 | 0.91 |
| 資産4 | -0.29 | 0.73 | 0.11 | 0.91 | 1 |
2.3.2 自動化
1資産の場合の数が$n$通りとすると5資産の場合の数は$n^5$となり、手動で投資比率を設定するのはきつい。そこで、for文で投資比率の組み合わせの設定を自動化する。これにとても時間がかかってしまっているのでもっといい方法があれば是非教えていただきたい。
"""
5資産の投資比率の組み合わせの設定
"""
n=5 # 資産の数
nmax=10 # 投資比率の精度
x=[0]*n # 配列の設定
for x0 in range(0,nmax):
x[0]=x0/nmax
for x1 in range(0,nmax):
x[1]=x1/nmax
for x2 in range(0,nmax):
x[2]=x2/nmax
for x3 in range(0,nmax):
x[3]=x3/nmax
if x[1]+x[2]+x[3]+x[4]>1: # 投資比率が100%を超えているとき
break
else:
x[4]=1-(x[1]+x[2]+x[3]+x[4])
print(x)
nmaxを大きくすれば細かい投資比率を出すことができるが、計算時間が長くなる。nmax=10か20くらいならすぐだが、100にするとまあまあ時間がかかる。資産の期待収益率、標準偏差、相関係数は将来大きく変動する可能性が高いことを考えると、細かい投資比率を求めたところで意味がないので、nmax=10で十分な気はする。上記のプログラムをもう少し改善したものが以下のものになる。
# -*- coding: utf-8 -*-
"""
5資産の投資比率の組み合わせの設定
"""
n=5 # 資産の数
nmax=10 # 投資比率の精度
x=[0]*n # 配列の設定
for x0 in range(0,nmax):
x[0]=x0/nmax
for x1 in range(0,nmax):
x[1]=x1/nmax
count=x[0]+x[1]
if count>1: # 投資比率が100%を超えているとき
break # この内側のfor文を抜ける
for x2 in range(0,nmax):
x[2]=x2/nmax
count=x[0]+x[1]+x[2]
if count>1: # 投資比率が100%を超えているとき
break # この内側のfor文を抜ける
for x3 in range(0,nmax):
x[3]=x3/nmax
count=x[0]+x[1]+x[2]+x[3]
if count>1: # 投資比率が100%を超えているとき
break # この内側のfor文を抜ける
else:
x[4]=1-count
print(x)
2.4 全体のプログラム
今までのことを統合すると、以下のプログラムになる。
# -*- coding: utf-8 -*-
"""
5資産の最適なアセットアロケーションを計算
"""
import numpy as np
# -------------------------------------------------
# input data
# -------------------------------------------------
r = [1.00,4.80,3.50,5.00,9.25] # 期待収益率
rho = [[1,0.16,-0.06,-0.05,-0.29],
[0.16,1,-0.25,0.27,0.73],
[-0.06,-0.25,1,0.56,0.11],
[-0.05,0.27,0.56,1,0.91],
[-0.29,0.73,0.11,0.91,1]] # 相関係数
sigma=[5.4,22.15,13.25,19.59,26.25] # 標準偏差
# -------------------------------------------------
# 本文
# -------------------------------------------------
n=5 # 資産の数
rmin=4 # 最低限欲しいと思う期待収益率
nmax=100 # 投資比率の精度(大きいほど精度が高くなるが計算時間は長くなる)
x=[0]*n # 配列の器の設定
xmin=[0]*n # xは逐次更新されてしまうので別で保存するための配列
sigmap_min=1000000 # 適当に大きい値を設定
err=1e-6 # 許容する誤差
for x0 in range(0,nmax):
x[0]=x0/nmax
for x1 in range(0,nmax):
x[1]=x1/nmax
count=x[0]+x[1]
if count>1+err: # 投資比率が100%を超えているとき
break # この内側のfor文を抜ける
for x2 in range(0,nmax):
x[2]=x2/nmax
count=x[0]+x[1]+x[2]
if count>1+err: # 投資比率が100%を超えているとき
break # この内側のfor文を抜ける
for x3 in range(0,nmax):
x[3]=x3/nmax
count=x[0]+x[1]+x[2]+x[3]
if count>1+err: # 投資比率が100%を超えているとき
break # この内側のfor文を抜ける
x[4]=round(1-count,6) # 誤差があるので1E-6で四捨五入
#------------------------
# 期待収益率
#------------------------
rp=0
for i in range(0,n):
rp+=r[i]*x[i]
if rp<rmin: # 最低限欲しいと思う期待収益率未満の場合
break
if rp>rmin+0.1: # 計算時間短縮のため
break
#------------------------
# 標準偏差
#------------------------
sigmap=0
for i in range(0,n):
for j in range(0,n):
sigmap+=rho[i][j]*sigma[i]*sigma[j]*x[i]*x[j]
if sigmap<sigmap_min:
sigmap_min=sigmap # 標準偏差(ここではまだ分散)をより小さい値に更新
xmin[:]=x[:] # 標準偏差が最小のときのxを別の配列に保存
rpt=rp # 期待収益率を別で保存
sigmap_min=np.sqrt(sigmap_min) # 分散から標準偏差に変換
print('ポートフォリオの期待収益率 {:.2f}'.format(rpt))
print('ポートフォリオの標準偏差 {:.2f}'.format(sigmap_min))
print('最適な投資比率',xmin)
出力結果:ポートフォリオの期待収益率 4.00
ポートフォリオの標準偏差 8.26
最適な投資比率 [0.42, 0.0, 0.31, 0.0, 0.27]
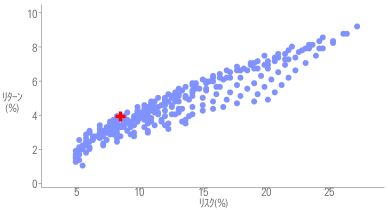
上記のプログラムはrminの値を変えることで様々な期待収益率に対する最適な投資比率をもとめることができる。この数字をツールにinputすることで、以下のように効率的フロンティア曲線に乗っていることを確認できる。[3]
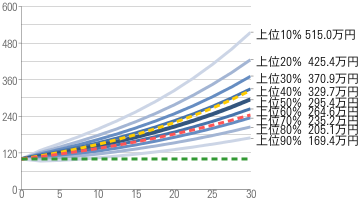

期待リターン:4.00% リスク:8.26%
元本:100万円 総投資額:0万円 期間:30年
(期待値:324.6 標準偏差:147.9 中央値:295.4 最頻値:244.6)
Future Work
- 任意の資産の数での計算の実現。5以下の資産に限定されているが、for文をたくさん書けばごり押しで拡張できる。
- 計算時間の短縮。CやFortranで書いた方が早いのだろうなと思う。
- 対数正規分布の考慮。算術平均の期待収益率が高くとも、標準偏差が過大であれば、幾何平均の期待収益率は低下してしまう。単純に私の知識不足で実現できていない。例えば、20年後の期待収益率を求めるときに必要になる。株価が対数正規分布に従うことについては[4]などを参照。