解釈可能なルールを学習するskope-rulesのアルゴリズム 〜Microsoft ResearchのlnterpretMLからも使えるよ〜

skope-rules というルール学習ライブラリを見つけました。 scikit-learn-contrib のプロジェクトです。
試しに、みんな大好きアイリスデータセットのサンプルコードを実行してみると次のようなルールが得られます。

Rules for iris virginica
('petal_length > 4.75 and petal_width > 1.75', (0.9743589743589743, 0.9047619047619048, 1))
('petal_width > 1.6500000357627869', (0.9514316093263462, 0.9218081435472739, 3))
('petal_length > 5.049999952316284', (0.9696691176470589, 0.8007518796992481, 2))

1 行 1 ルールになっていて、たとえば最初のルール petal_length > 4.75 and petal_width > 1.75 は virginica の分類について precision が約 0.97 、recall が約 0.90 、学習の元になった決定木での出現回数が 1 回というふうに読みます。なるほどなー。

ルール学習の使い所

さて、上記の「元になった決定木」というところで普通に決定木で分類すればよくね？と思った右や左の旦那様、ええ、複雑な決定木で推論できる環境なら XGBoost なり LightGBM で精度出せばよろしいのですが、そうはいかない現場もあります＞＜

• エッジに複雑な決定木が組み込めない
• 稀に想定外の誤推論をするような挙動が許されない
• 推論時と同等のデータセットや検証環境が学習時に用意できない

などなど精度よりも解釈可能なシンプルなルールが求められる場合ですね。
なおかつ特徴量がたくさんあって人の当て勘で試行錯誤するのは辛いのでマイニングしたい、といった時にこういうルール学習はハマるのではないかと思います。

skope-rules のアルゴリズム

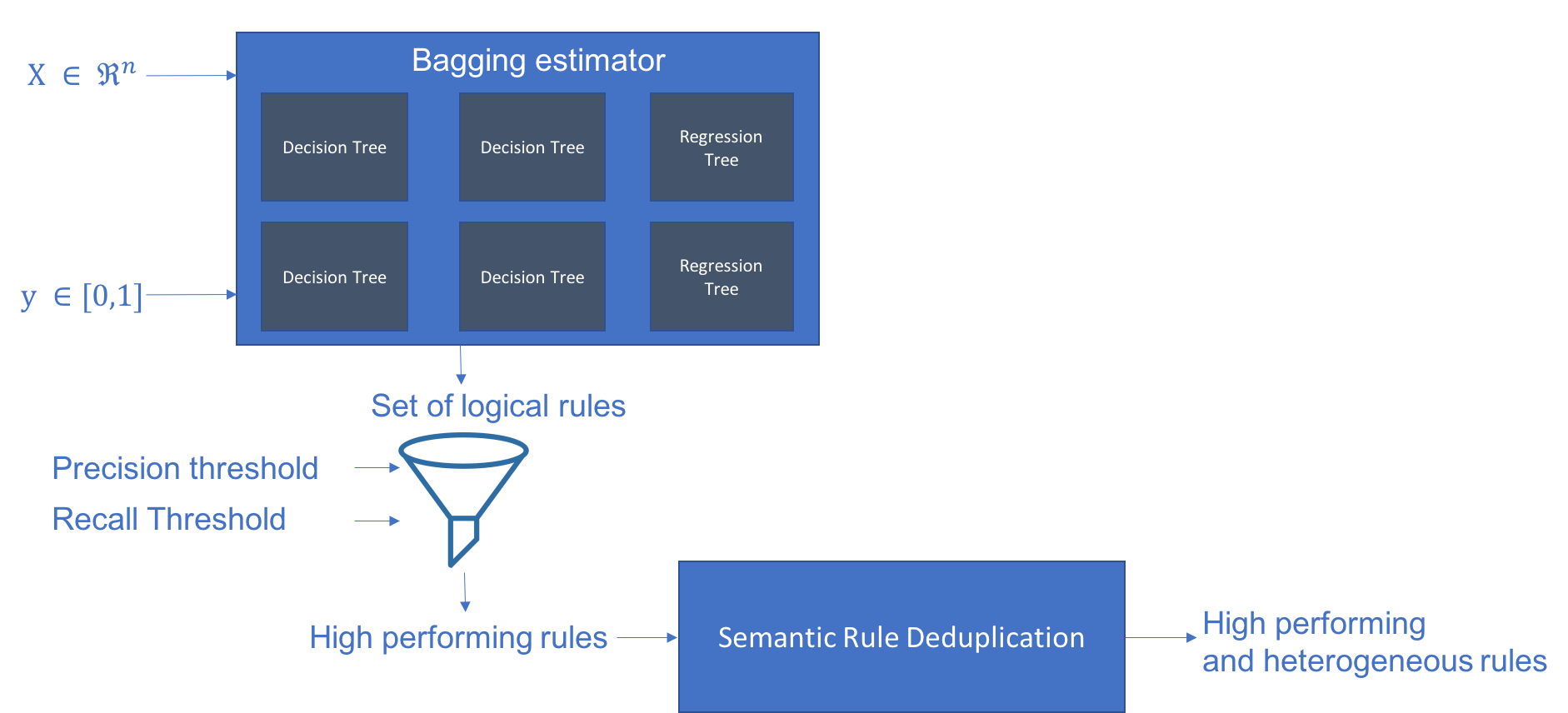
アルゴリズム概観は README の図が分かりやすいので引用します。

skope-rules/schema.png

つまり決定木をたくさん学習して、それらをバラして大量のルール候補を手に入れ、フィルタリングしたり似たものを排除したうえで精度のいいものを出力する流れですね。この細かいところをコードから読み解いてみました、というのが本記事の趣旨になります。
といっても、本体は 700 行に満たないファイル一つなので流れは追いやすいです。

Bagging estimator

まず初めに分類木と回帰木それぞれをバギングして、さらに深さの設定も変えながら元となる決定木をたくさん作りだします。
skope-rules が扱うのは二値分類なのですが、サンプルの重みを渡すことで擬似的な回帰問題としても扱っています。ただし重みを渡さないときは回帰木も 0/1 で学習します。
分類木だけでなく回帰木も学習することが最終的なルールにどのくらい寄与しているかどうかは不明ですが、どうせ精度悪いルールは後で落とすので、とりあえずルール候補を増やすために突っ込んでおけな雰囲気は感じます。

コードとしては、

for max_depth in self._max_depths:
    bagging_clf = BaggingClassifier(
        base_estimator=DecisionTreeClassifier(
           max_depth=max_depth,
...
    bagging_reg = BaggingRegressor(
        base_estimator=DecisionTreeRegressor(
            max_depth=max_depth,

skope-rules/skrules/skope_rules.py　　※ 読みやすさのため整形して引用

という感じで、 scikit-learn の決定木クラスを利用しています。そのためカテゴリカル変数や欠損値が扱えない欠点はそのまま引き継いでしまっています……。
このあたりは scikit-learn 本体でカテゴリカル変数対応中みたいなので、そのうち解消されるかもしれません。
https://github.com/scikit-learn/scikit-learn/pull/12866

-> Set of logical rules

決定木を根っこから葉っぱまで辿って、そのパス一つ一つに対して分岐条件を AND で繋いでルール化します。

def recurse(node, base_name):
    if tree_.feature[node] != _tree.TREE_UNDEFINED:
        name = feature_name[node]
        symbol = '<='
        symbol2 = '>'
        threshold = tree_.threshold[node]
        text = base_name + ["{} {} {}".format(name, symbol, threshold)]
        recurse(tree_.children_left[node], text)
        text = base_name + ["{} {} {}".format(name, symbol2, threshold)]
        recurse(tree_.children_right[node], text)
    else:
        rule = str.join(' and ', base_name)
        rule = (rule if rule != '' else ' == '.join([feature_names[0]] * 2))
        rules.append(rule)

skope-rules/skrules/skope_rules.py

再帰関数で辿っているので、これは深さ優先探索ですね。

-> High performing rules

ルールごとに、元になった決定木の Out-of-Bag データに対して precision と recall を計算して、設定した最低値より高いルールだけを残します。

ここでちょっと面白いのが、ルールに当てはまっているかどうかの判定に元の決定木を使うのではなく、

def _eval_rule_perf(self, rule, X, y):
    detected_index = list(X.query(rule).index)

skope-rules/skrules/skope_rules.py

として pandas.DataFrame.query に食わせているところです。 skope-rules 内でルールは petal_length > 4.75 and petal_width > 1.75 といった文字列として持ちつづけているので、そのままクエリとして扱うことができます。ただ後述の特徴量リストアップする時に文字列を split しなおしてているので、ちょっと実装いけてない感じはありますが。

Semantic Rule Deduplication

前述で生き残ったルールのうち似ているものをグルーピングして、グループごとに F1 スコアの最も良いルールを残します。これがないと閾値だけ微妙に異なるルールがいくつも出力されてしまうのですね。

似てるかどうかは、

def split_with_best_feature(rules, depth, exceptions=[]):
...
    for rule in rules:
        if (most_represented_term + ' <=') in rule[0]:
            rules_splitted[0].append(rule)
        elif (most_represented_term + ' >') in rule[0]:
            rules_splitted[1].append(rule)
        else:
            rules_splitted[2].append(rule)
        new_exceptions = exceptions+[most_represented_term]
        return [split_with_best_feature(ruleset, depth-1, exceptions=new_exceptions)
                for ruleset in rules_splitted]

skope-rules/skrules/skope_rules.py

というふうによく使われている特徴量とその不等号を順に見ていって、設定した深さまで一緒だったら同じグループに仕分ける感じになっています。

lnterpretMLから呼んでみる

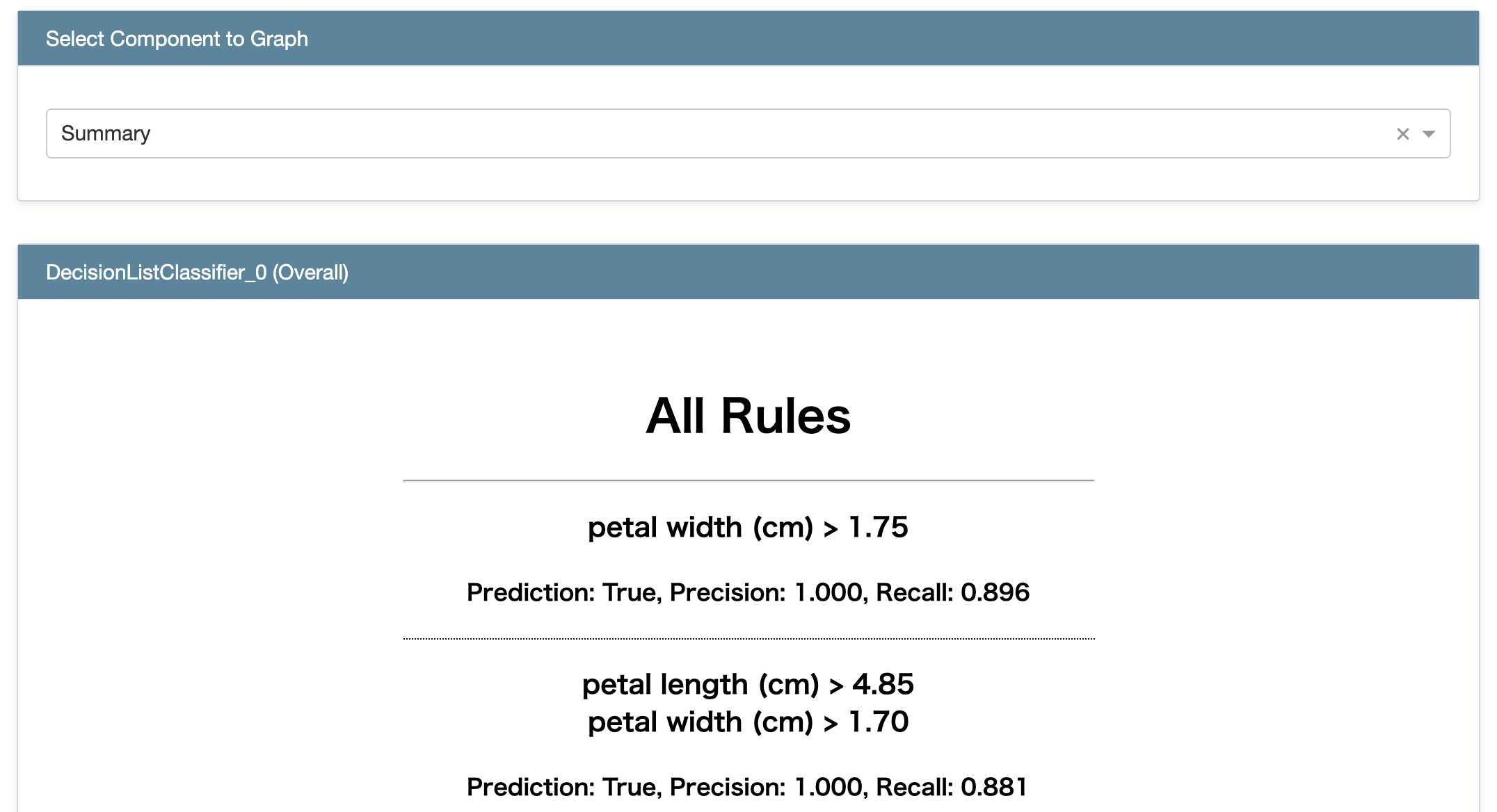
さて skope-rules は、Microsoft Research が開発しているパッケージ lnterpretML に組み込まれているので、そちらからも呼びだしてみます。 DecisionListClassifier というクラスが skope-rules のラッパーです。

from interpret.glassbox import DecisionListClassifier
from interpret import show
from sklearn.datasets import load_iris
import pandas as pd

iris = load_iris()
dlc = DecisionListClassifier()
dlc.fit(pd.DataFrame(iris.data, columns=iris.feature_names),
        iris.target == iris.target_names.tolist().index('virginica'))
show(dlc.explain_global())

解釈性のためのパッケージだけあって、見栄えがいいですね。

雑感

最近、機械学習モデルの解釈性に興味があります。解釈性の現状については『機械学習モデルの判断根拠の説明（Ver.2）』に詳しいです。
一口に解釈性といっても、それを求める理由は色々とあって lnterpretML の interpret/README では、

• デバッグ：推論を外した理由は？
• 公平性：差別的なモデルになってないか？
• 人との協業：どうすればモデルを理解して信頼できるか？
• コンプライアンス：法の要件を満たしているか？
• ハイリスク領域：医療、金融、司法……

と書かれています。業務によってポイントは変わってくると思うのですが、個人的なモチベーションはやはりモデルが発見した知識を自分も獲得したい、そこに自分なりの思考や勘を入れこんで知識をアレンジしたり転用したりしたい、というところにある気がしています。
そういう目的では、やはり複雑なモデルをどうにかするのではなく初めから「説明が不要な可読なモデル」を学習するべきかと思うのですが、そうなると使える手法ってどのくらいあるんだっけという話で、『Interpretable Machine Learning - Chapter 4 Interpretable Models』では線形回帰・ロジスティック回帰・一般化線形モデル・一般化加法モデル・決定木・RuleFit・ナイーブベイズ・k近傍法などが挙げられています。 RuleFit は skope-rules と同じように決定木からルールを得るのですが、それらをさらに線形回帰の特徴量として使うところが異なります。
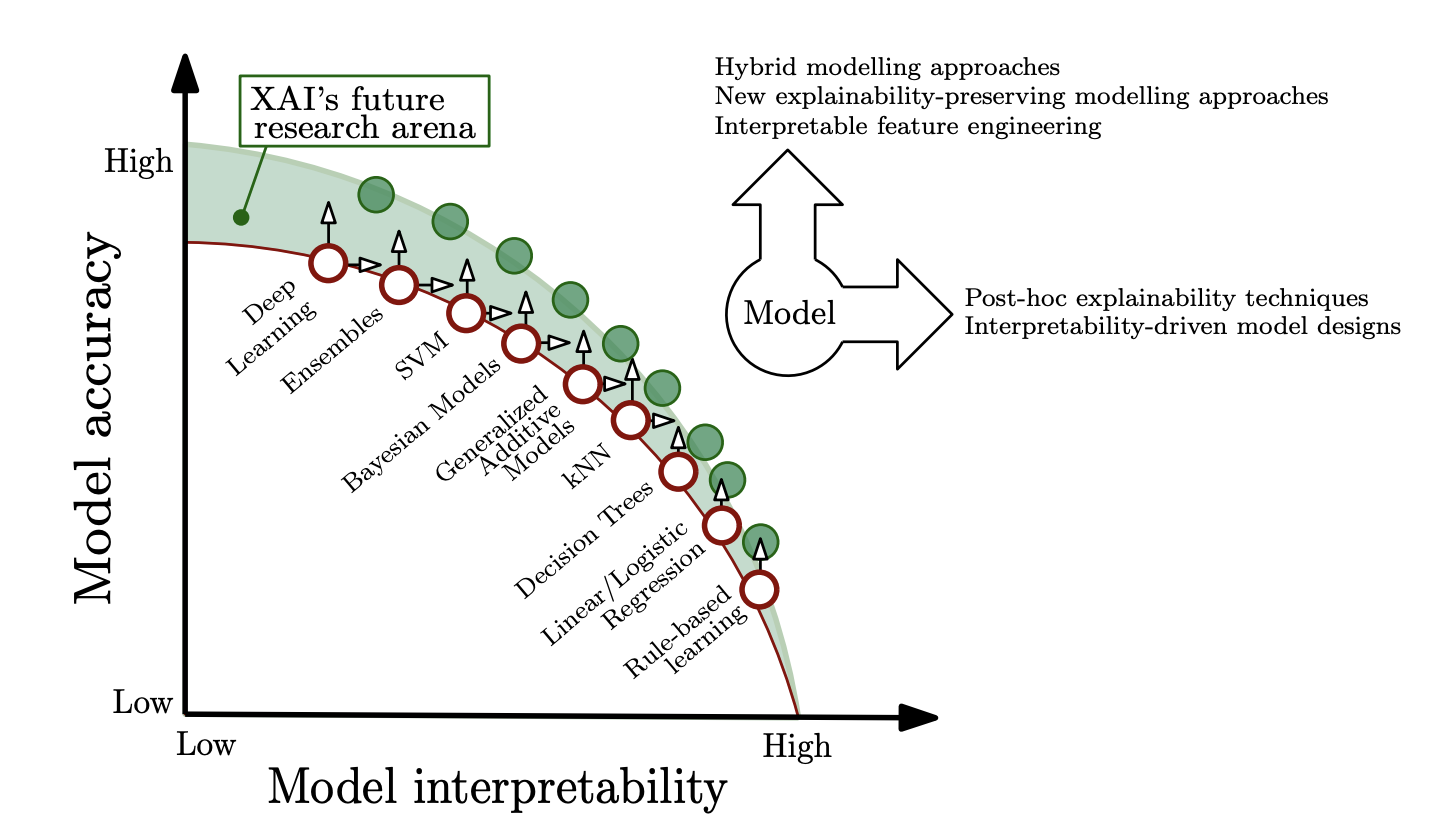
ここで、もちろんモデルの精度と解釈性にはトレードオフがあるはずで『機械学習の説明可能性（解釈性）という迷宮』で紹介されていた『Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI』の図が気持ちとしては分かりやすいので引用します。

そのため完璧な解釈性を求めても不毛な領域はあるはずで、ディープラーニングが成功を収めている画像とか自然言語といったドメインでは戦う相手が人間の認知能力なのでモデルが複雑怪奇になるのもむべなるかなと思うのですが、伝統的に綺麗な計算式で現象を捉えている物理的だったり工学的なドメインではもうちょっといい感じにバランスとれた手法が眠ってるんじゃないかという希望的観測を抱いています。
十年前くらいに『物理法則を自力で発見した人工知能』として遺伝的プログラミングが話題になりましたが、こんなふうに小さな計算グラフを学習できるといいなぁと。『遺伝的プログラミングによる特徴量生成』のように特徴量生成で使うなら色んな手法と組み合わせられるので、このあたり活路ないかなぁと期待してみる今日この頃です。