遺伝的プログラミングによる特徴量生成

この記事では遺伝的プログラミングを用いた特徴量生成について紹介します。

概要

統計モデルの精度を向上させるためには、目的変数の特徴を上手く表現するような変数を見つけることが重要になります。特徴量の探索としては、ベースとなる説明変数を用意した上でそれらの交互作用項や対数変換項などを特徴量に加え、変数選択や次元圧縮をするという方法がよく取られますが、検証する変数が膨大になりやすく総当り的な探索が難しくなる上に、次元圧縮の手法選択やパラメータ調整も重要になるので工数が膨大になることも多いと思います。そこで別種のアプローチとして遺伝的プログラミングを用いてモデル精度を向上させるような変数を逐次的に生成し、段階的に精度を向上させる方法について検討してみました。

遺伝的アルゴリズムについて

遺伝的プログラミングの前に遺伝的アルゴリズムについて簡単に説明したいと思います。

遺伝的アルゴリズムは生物界の進化の仕組みを模倣したメタヒューリスティックな近似解探索アルゴリズムで、比較的短時間でそこそこ良い精度の解を得ることが可能です。基本的な流れとしては、データを遺伝子で表現した個体を複数用意し、適応度の高い個体を優先的に選択し、交叉や突然変異などの操作を繰り返しながら解を探索していきます。主な特徴は評価関数に関して可微分性や単峰性といった知識が無くとも利用可能な点で、組み合わせ最適化問題やNP困難な問題に広く利用されています。

イメージとしては下記のようなプロセスを繰り返すことで準最適解を求めていきます。

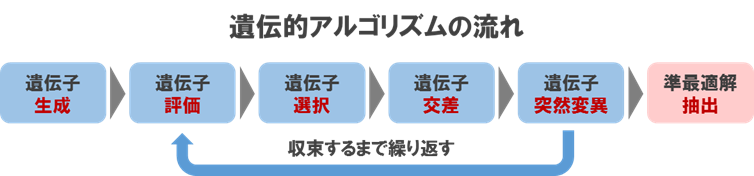
進化の過程において選択／交叉／突然変異といった操作を行うわけですが、これに関しては様々な方法が提案されており、代表的なものは下記になります。

• 選択
  • トーナメント方式
    • 集団からランダムに個体を複数抽出し、その中で最も適応度の高い個体を選択する方法
  • ルーレット選択
    • 適応度に応じた確率で個体を選ぶ方法
• 交叉
  • 2点交叉
    • 交差点をランダムに二つ選び、はさまれている部分を入れ替える方法
  • 一様交叉
    • 各要素を独立に1/2の確率で入れ替える方法
• 突然変異
  • ランダム変異
    • 個体の遺伝子の一部をランダムに入れ替える方法
  • スクランブル
    • ランダムに選ばれた2点間の要素の順序をランダムに並べ替える方法

遺伝的プログラミングについて

遺伝的プログラミングは遺伝的アルゴリズムの拡張として提案された手法で、遺伝的アルゴリズムが解を直接求めるのに対して、遺伝的プログラミングでは解を求める手続きを求めることが可能という特徴があります。具体的な内容としては、遺伝子の表現に木構造を用いており、これにより遺伝的アルゴリズムでは表現できなかった数式やプログラムコードなどの構造を持ったデータを表現することができます。
例えば、次のような木構造は$x \times (2 - x)$を表現しています。

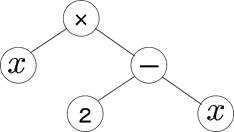
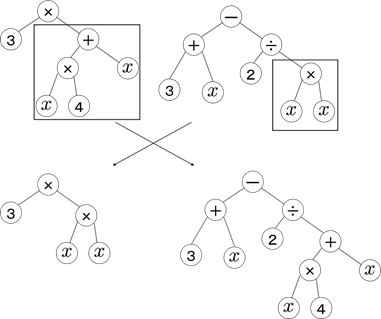
遺伝子操作は選択に関しては遺伝的アルゴリズムと同様ですが、交叉や突然変異は下記のように行います。

• 交叉
  • ランダムに選んだノードに関して、部分木を入れ替える

• 突然変異
  • ランダムに選んだノードに関して、ランダムに生成した部分木に入れ替えたり、削除したりする

遺伝的プログラミングを用いた特徴量生成

遺伝的プログラミングによって様々な演算を組み合わせた関数を生成できる特徴を用いて、モデルの精度を向上させるような特徴量を関数として生成することを試みます。

基本的なアイデアとしては、モデルの評価指標を適合度としてベースとなる説明変数セットから各変数の四則演算や変数変換を用いて新たな変数を多数生成し、遺伝的プログラミングを用いて進化させ、この変数を元のデータセットに追加して評価指標が最も向上する変数を追加するという処理を繰り返していきます。規定回数進化させても精度が向上しない場合は生成した変数を既存の変数セットに追加せずにRejectして再度変数生成を行うことにし、精度向上が見込める場合のみAcceptして変数セットに追加することで、単調に精度が向上するようにします。

具体的な手順は下記の通りです。

1. 基本的な演算子からなる構文木を多数生成する。
2. 各構文木から作られる変数を元のデータセットに追加して、5-foldクロスバリデーションによりAUCを計算する。
3. 選択、交差、突然変異により規定世代に達するまで進化させる。
4. 規定世代に達した際、最大適応度個体のAUCが元のデータセットのAUCを超えていた場合Acceptとし、超えていなかった場合Rejectとする。
5. Acceptの場合は元のデータセットに変数を追加して次の変数生成に移り、Rejectの場合は再度変数生成を試みる。
6. 上記1～5の手順を繰り返す。

実装

今回はdeapというpythonパッケージを利用しています。このパッケージは汎用的な遺伝的アルゴリズム/プログラミング用のツールで、比較的簡単に遺伝的手法の実装が可能です。pip install deapで簡単にインストールできます。

検証に用いるデータは、scikit-learnのサンプルジェネレータであるmake_classificationにより生成することにします。make_classificationはデータサイズや特徴量数、複雑さなどを調整可能なため、アルゴリズムをテストする際に便利です。今回はサンプルデータとして特徴量数10の2値分類用データを10,000件生成し、8,000件を学習用、残り2,000件をテスト用として検証を行うことにします。

X, y = make_classification(n_samples=10000, n_features=10, n_informative=10, n_redundant=0, 
                           n_repeated=0,n_clusters_per_class=8, random_state=123)

また、ベースとするモデルはL2正則化ロジスティック回帰とし、評価方法は学習データの5-foldクロスバリデーションAUCとテストデータのAUCとすることにします。進化の過程で高次項が生成されやすいので、適合度指標の計算においてクロスバリデーションを用いた方がオーバーフィットが起こり難く安全です。

構文木を遺伝的プログラミングで進化させる際のパラメータ設定は下記としました。

• 生成個体数：300
• トーナメントサイズ：10（トーナメント選択）
• 交叉確率：0.5
• 突然変異確率：0.1
• 進化世代数：10
• 構文木に利用する演算子：＋、－、×、÷、neg（±変換）、sin、cos、tan（÷は分母が0で発散する場合は1に置換）
• 構文木の最大の深さ：5

実行コードは下記になります。

import operator, math, random, time
import numpy as np

from deap import algorithms, base, creator, tools, gp

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score, log_loss

import matplotlib.pyplot as plt

# サンプルデータの生成
X, y = make_classification(n_samples=10000, n_features=10, n_informative=5, n_redundant=0, n_repeated=0,
                           n_clusters_per_class=8, random_state=123)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)

# ベースラインスコアの算出
clf = LogisticRegression(penalty="l2", C=1.0)
base_train_auc = np.mean(cross_val_score(clf, X_train, y_train, scoring="roc_auc", cv=5))
clf.fit(X_train, y_train)
base_test_auc = roc_auc_score(y_test, clf.predict_proba(X_test)[:,1])

# 除算関数の定義
# 左項 / 右項で右項が0の場合1を代入する
def protectedDiv(left, right):
    eps = 1.0e-7
    tmp = np.zeros(len(left))
    tmp[np.abs(right) >= eps] = left[np.abs(right) >= eps] / right[np.abs(right) >= eps]
    tmp[np.abs(right) < eps] = 1.0
    return tmp


# 乱数シード
random.seed(123)

# 適合度を最大化するような木構造を個体として定義
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMax)

# 初期値の計算
# 学習データの5-fold CVのAUCスコアを評価指標の初期値とする
n_features = X_train.shape[1]
clf = LogisticRegression(penalty="l2", C=1.0)
prev_auc = np.mean(cross_val_score(clf, X_train, y_train, scoring="roc_auc", cv=5))

# メインループ
# resultsに特徴量数、学習データのAUCスコア（5-fold CV）、テストデータのAUCスコアを保持する
# exprsに生成された特徴量の表記を保持する
results = []
exprs = []
for i in range(100):
    # 構文木として利用可能な演算の定義
    pset = gp.PrimitiveSet("MAIN", n_features)
    pset.addPrimitive(operator.add, 2)
    pset.addPrimitive(operator.sub, 2)
    pset.addPrimitive(operator.mul, 2)
    pset.addPrimitive(protectedDiv, 2)
    pset.addPrimitive(operator.neg, 1)
    pset.addPrimitive(np.cos, 1)
    pset.addPrimitive(np.sin, 1)
    pset.addPrimitive(np.tan, 1)

    # 関数のデフォルト値の設定
    toolbox = base.Toolbox()
    toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=3)
    toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
    toolbox.register("population", tools.initRepeat, list, toolbox.individual)
    toolbox.register("compile", gp.compile, pset=pset)

    # 評価関数の設定
    # 新しく生成した変数を元の変数に加えて5-fold CVを求める
    def eval_genfeat(individual):
        func = toolbox.compile(expr=individual)
        features_train = [X_train[:,i] for i in range(n_features)]
        new_feat_train = func(*features_train)
        X_train_tmp = np.c_[X_train, new_feat_train]
        return np.mean(cross_val_score(clf, X_train_tmp, y_train, scoring="roc_auc", cv=5)),

    # 評価、選択、交叉、突然変異の設定
    # 選択はサイズ10のトーナメント方式、交叉は1点交叉、突然変異は深さ2のランダム構文木生成と定義
    toolbox.register("evaluate", eval_genfeat)
    toolbox.register("select", tools.selTournament, tournsize=10)
    toolbox.register("mate", gp.cxOnePoint)
    toolbox.register("expr_mut", gp.genFull, min_=0, max_=2)
    toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)

    # 構文木の制約の設定
    # 交叉や突然変異で深さ5以上の木ができないようにする
    toolbox.decorate("mate", gp.staticLimit(key=operator.attrgetter("height"), max_value=5))
    toolbox.decorate("mutate", gp.staticLimit(key=operator.attrgetter("height"), max_value=5)) 

    # 世代ごとの個体とベスト解を保持するクラスの生成
    pop = toolbox.population(n=300)
    hof = tools.HallOfFame(1)

    # 統計量の表示設定
    stats_fit = tools.Statistics(lambda ind: ind.fitness.values)
    stats_size = tools.Statistics(len)
    mstats = tools.MultiStatistics(fitness=stats_fit, size=stats_size)
    mstats.register("avg", np.mean)
    mstats.register("std", np.std)
    mstats.register("min", np.min)
    mstats.register("max", np.max)

    # 進化の実行
    # 交叉確率50%、突然変異確率10%、10世代まで進化
    start_time = time.time()
    pop, log = algorithms.eaSimple(pop, toolbox, 0.5, 0.1, 10, stats=mstats, halloffame=hof, verbose=True)
    end_time = time.time()

    # ベスト解とAUCの保持
    best_expr = hof[0]
    best_auc = mstats.compile(pop)["fitness"]["max"]
    
    # 5-fold CVのAUCスコアが前ステップのAUCを超えていた場合
    # 生成変数を学習、テストデータに追加し、ベストAUCを更新する
    if prev_auc < best_auc:
        # 生成変数の追加
        func = toolbox.compile(expr=best_expr)
        features_train = [X_train[:,i] for i in range(n_features)]
        features_test = [X_test[:,i] for i in range(n_features)]
        new_feat_train = func(*features_train)
        new_feat_test = func(*features_test)
        X_train = np.c_[X_train, new_feat_train]
        X_test = np.c_[X_test, new_feat_test]
        
        ### テストAUCの計算（プロット用）
        clf.fit(X_train, y_train)
        train_auc = roc_auc_score(y_train, clf.predict_proba(X_train)[:,1])
        test_auc = roc_auc_score(y_test, clf.predict_proba(X_test)[:,1])

        # ベストAUCの更新と特徴量数の加算
        prev_auc = best_auc
        n_features += 1

        # 表示と出力用データの保持
        print(n_features, best_auc, train_auc, test_auc, end_time - start_time)
        results.append([n_features, best_auc, train_auc, test_auc])
        exprs.append(best_expr)

        # 変数追加後の特徴量数が30を超えた場合break
        if n_features >= 30:
            break

# 結果の出力
print()
print("### Results")
print("Baseline AUC train :", base_train_auc)
print("Baseline AUC test :", base_test_auc)
print("Best AUC train :", results[-1][1])
print("Best AUC test :", results[-1][3])

# 結果のプロット
res = np.array(results)
plt.plot(res[:,0], res[:,1],"o-", color="b", label="train(5-fold CV)")
plt.plot(res[:,0], res[:,3],"o-", color="r", label="test")
plt.plot(10, base_train_auc, "d", color="b", label = "train baseline(5-fold CV)")
plt.plot(10, base_test_auc, "d", color="r", label = "test baseline")
plt.xlim(9,31)
plt.grid(which="both")
plt.xlabel('n_features')
plt.ylabel('AUC')
plt.legend(loc="lower right")
plt.savefig("gp_featgen.png")

# 生成した構文木の出力
print()
print("### Generated feature expression")
for expr in exprs:
    print(expr)

結果

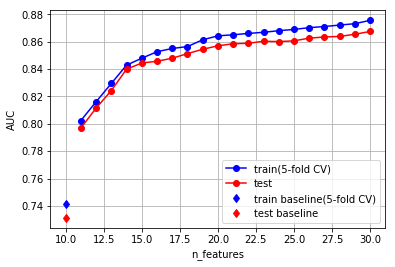
データの特徴量数が10変数から30変数になるように、20変数生成させた場合の学習データのAUC（5-fold CV）とテストデータのAUCは下記のようになりました。

### Results
Baseline AUC train : 0.741195900486
Baseline AUC test : 0.731194743417
Best AUC train : 0.875623225397
Best AUC test : 0.867496316228

特徴量が増えるに従って精度が向上しているのが見て取れます。14変数ぐらいまでは比較的大きく精度が向上していますが、それ以降は改善幅が小さくなっており、段々精度が向上し難くなっています。
生成された変数（構文木）は下記になります。

### Generated feature expression
mul(sub(add(mul(ARG9, ARG2), cos(neg(ARG6))), neg(ARG6)), sub(ARG7, cos(cos(neg(ARG6)))))
mul(neg(ARG10), mul(ARG9, ARG8))
sub(add(ARG1, ARG8), add(mul(add(ARG2, ARG6), ARG8), cos(protectedDiv(ARG10, ARG3))))
sub(sub(sub(neg(mul(ARG9, ARG12)), cos(ARG9)), cos(ARG9)), mul(ARG2, ARG12))
mul(add(add(ARG6, neg(ARG7)), ARG8), add(sin(ARG6), neg(ARG7)))
sin(cos(add(ARG8, ARG2)))
cos(cos(add(cos(ARG9), sin(sin(ARG2)))))
mul(ARG8, mul(mul(mul(mul(ARG16, ARG16), mul(ARG16, ARG16)), ARG16), ARG16))
mul(sub(ARG17, add(add(ARG9, ARG2), sin(ARG2))), add(ARG16, ARG14))
add(sub(mul(mul(ARG8, ARG7), ARG7), mul(ARG14, ARG8)), mul(ARG8, ARG7))
cos(ARG7)
add(mul(ARG10, ARG6), mul(mul(ARG10, ARG6), ARG6))
protectedDiv(ARG19, ARG17)
add(mul(ARG2, ARG20), mul(ARG10, ARG2))
sin(add(add(ARG6, tan(ARG16)), tan(ARG9)))
mul(neg(ARG2), sub(sub(sub(sub(ARG18, ARG19), ARG6), ARG6), ARG6))
mul(cos(tan(cos(ARG6))), ARG16)
sub(cos(ARG6), mul(ARG7, ARG2))
mul(ARG16, sin(ARG27))
mul(sub(ARG27, ARG15), add(ARG8, add(ARG9, ARG6)))

上記はLispのS式で記述されており、例えば、sin(mul(ARG1, ARG2))は$\sin(x_1 \times x_2)$を意味しています。
sinやcosを複雑に組み合わせた変数が生成されていたり、人間が中々思いつかないような変数も探索可能な点がこのアプローチの面白い点だと思います。

検討

既存の説明変数セットから単純にモデル精度を上げるような変数を生成したい場合に、それなりに使えるのではないかと思います。ただし進化の過程で非常に膨大なモデルを学習する必要があるので、データサイズや特徴量数が大きい場合や複雑なモデルを使いたい場合は、計算コスト的にかなり苦しくなります。今回はロジスティック回帰モデルを使っていましたが、それでも説明変数が増えるに従って指数関数的に速度が遅くなっていくので、20変数の生成でも数時間かかってしまいました。また、遺伝的プログラミングのパラメータも結構な数があるので、場合によっては調整に時間がかかることも懸念されます。実際に利用する際はサンプリングでデータサイズを減らしたり、一部の特徴量のみを利用するなどの工夫を行った方が良いかもしれません。

まとめ

遺伝的プログラミングを用いてモデル精度を向上させる特徴量生成を試みました。サンプルデータに対してロジスティック回帰を用いてテストしたところ、実際に逐次的にモデル精度を改善するような変数を生成することができました。ただし進化計算にかなりの計算コストが必要になるので実際に利用する際は注意が必要と考えられます。非線形モデルほど良いとまでは言えませんが、演算や処理の定義次第で様々なパターンの変数が作れるので、精度改善を行いたいときに追加特徴量の生成として試してみるのはありなのではないでしょうか。