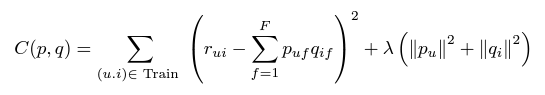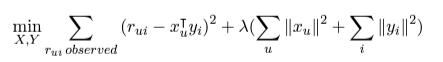概要
今回は、レコメンド分野でよく利用される行列分解のアルゴリズムである Funk-SVD, ALS(Alternating Least Squares) を実装したので、その内容を備忘録的にまとめます。
はじめに
私は情報系の大学院に通う傍ら、ECサイトを運営する企業でインターンをしております。
そして、そこで取り組んでいる主な業務内容がレコメンドシステム開発です。
とはいえ、レコメンドについて研究しているわけでもなく、アルゴリズムの実装もライブラリ任せなところがありました。
そこで今回は勉強のために、とても有名なレコメンドアルゴリズムである行列分解のうち、Funk-SVD, ALSの理論と実装を行いました。
そして、その内容を備忘録的にまとめていきたいと思います。
行列分解とレコメンド
行列分解とレコメンドの関係性について簡単にまとめます。
レコメンドとは、ECサイトや動画プラットフォームにおいて、 ユーザが好むと推定される
アイテム を提示することです。
そして、 ユーザが好むと推定されるアイテム を決めるためによく用いられるのが、
評価値行列 です。
評価値行列とは、行方向にユーザラベルを、列方向にアイテムラベルを並べ、各要素にはユーザのアイテムへの評価値を入れた行列のことです。
ここで、ユーザは全てのアイテムを評価するケースは(現実では)ほとんどないため、評価値行列は穴あきの行列となることが多いです。
しかしながら、レコメンドに重要なのはその穴あきの部分です。
穴あきの部分、つまりユーザが評価していないアイテムの評価値が分かれば、ユーザがまだ出会っていない(評価していない)アイテムをレコメンドすることが可能になります。
そして、穴あきの部分に推定された評価値を入れるために用いられるのが 行列分解 です。
行列分解では、評価値行列をユーザ因子行列とアイテム因子行列の2つの行列に分解します。
各因子行列には、全ての行列要素に何らかの値が入っているため、ユーザ因子行列から取り出したユーザベクトルと、アイテム因子行列から取り出したアイテムベクトルの内積をとることで、ユーザが評価していないアイテムの評価値を得ることができます。
その評価値を使えば、ユーザにレコメンドをすることができそうですね。
そして、それらの各因子行列の各要素の値を決定するためのアルゴリズムが、 Funk-SVD, ALSです。
以下でそれらについてまとめます。
Funk-SVD
Funk-SVDは、その名の通りFunkさんが考案したアルゴリズムです。
アルゴリズムの内容を以下に示します。
このアルゴリズムですが、基本的に行っていることとしては、以下の誤差関数を微分し勾配を求め、その勾配を使い繰り返し各因子行列の要素を更新するというものです。
以下に実装したコードを記します。
f = 10 # 潜在因子数
alpha = 0.01 # 学習率
l_reg = 0.1 # 正則化項の係数
n = 1000 # ループ数
mse_svd = [] # 学習中の評価関数
loss_svd = [] # 学習中の損失関数
# ユーザ因子行列(P),アイテム因子行列(Q)の初期化
P = np.zeros([f, user_num])
Q = np.zeros([f, item_num])
for i in range(f):
for j in range(user_num):
P[i, j] = random.uniform(0, 1 / np.sqrt(f))
for i in range(f):
for j in range(item_num):
Q[i, j] = random.uniform(0, 1 / np.sqrt(f))
# 行列要素の更新
for step in range(n):
for (u, i), r_ui in np.ndenumerate(ratings):
if not np.isnan(r_ui):
err_ui = r_ui - np.dot(P[:, u], Q[:, i])
for k in range(f):
P[k, u] += alpha * (Q[k, i] * err_ui - l_reg * P[k, u])
Q[k, i] += alpha * (P[k, u] * err_ui - l_reg * Q[k, i])
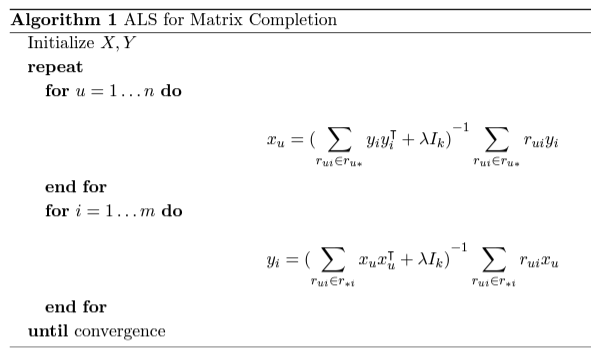
ALS(Alternating Least Square)
Funk-SVDには課題がありました。
それは、要素を1つずつ更新するため計算時間が非常に長いという点です。
それを解決する形で提案されたのがALSです。
ALSのアルゴリズムを以下に示します。
ALSは、因子行列の各要素の更新の際に、もう片方の因子行列を固定します。
(例えば、ユーザ因子行列の値を更新する場合には、アイテム因子行列を固定する)
そして、最小二乗誤差を求めて行列の各要素の値を更新します。
ちなみに、誤差関数は以下のものを使用します。
(各因子行列を交互に(Alternating)計算し、最小二乗誤差を求める(Least Square)というのが名前の由来らしい)
これらの処理は、並列に計算することができるため、計算時間が非常に短縮されます。
(ちなみに、計算量も削減されますがここでは割愛します)
以下に実装したコードを記します。
f = 10 # 潜在因子数
l_reg = 0.01 # 正則化項の係数
n = 1000 # ループ数
mse_als = [] # 学習中の評価関数
loss_als = [] # 学習中の損失関数
# ユーザ因子行列(P),アイテム因子行列(Q)の初期化
P = np.zeros([f, user_num])
Q = np.zeros([f, item_num])
for i in range(f):
for j in range(user_num):
P[i, j] = random.uniform(0, 1 / np.sqrt(f))
for i in range(f):
for j in range(item_num):
Q[i, j] = random.uniform(0, 1 / np.sqrt(f))
for step in range(n):
for u in range(ratings.shape[0]):
user_ratings_vector = np.zeros(f)
user_covariance_matrix = np.zeros([f, f])
for i in range(ratings.shape[1]):
if not np.isnan(ratings[u, i]):
user_ratings_vector += ratings[u, i] * Q[:, i]
user_covariance_matrix += np.outer(Q[:, i], Q[:, i])
user_covariance_matrix += np.eye(f) * l_reg
P[:, u] = np.dot(np.linalg.inv(user_covariance_matrix), user_ratings_vector.reshape(-1))
for i in range(ratings.shape[1]):
user_ratings_vector = np.zeros(f)
user_covariance_matrix = np.zeros([f, f])
for u in range(ratings.shape[0]):
if not np.isnan(ratings[u, i]):
user_ratings_vector += ratings[u, i] * P[:, u]
user_covariance_matrix += np.outer(P[:, u], P[:, u])
user_covariance_matrix += np.eye(f) * l_reg
Q[:, i] = np.dot(np.linalg.inv(user_covariance_matrix), user_ratings_vector.reshape(-1))
まとめ
今回は、レコメンド分野でよく用いられる行列分解のアルゴリズムであるFunk-SVD, ALSを実装しました。
どちらも、乱数で作成した評価値行列に対して適用したところ、うまく各因子行列を求めることができました。
今後は、ALSの発展版のアルゴリズムやその他のアルゴリズムの勉強をしたいと思います。
参考文献
Yuefeng Zhang, An Introduction to Matrix factorization and Factorization Machines in Recommendation System, and Beyond, https://arxiv.org/abs/2203.11026
Haoming Li, Bangzheng He, Michael Lublin, Yonathan Perez, CME 323: Distributed Algorithms and Optimization, Spring 2015, https://stanford.edu/~rezab/classes/cme323/S15/notes/lec14.pdf