Juliaで電子顕微鏡シミュレーション

　この記事では、Juliaを用いたマルチスライス法による電子顕微鏡シミュレーションについて書きます。マルチスライス法についてのイントロダクションとJuliaによる実際のプログラムについて主に書き、シミュレーションの数理については別の記事にまとめる予定です。

電子顕微鏡とマルチスライス法について

　電子顕微鏡とは、電子線を試料に照射することで試料の表面や内部の状態を知る顕微鏡のことです。試料によって反射される電子を捉え、観察する顕微鏡をSEM(走査型電子顕微鏡)、試料を透過した電子を捉える顕微鏡をTEM(透過型電子顕微鏡)といいます。今回はTEMについて取り扱います。
　TEMでは、試料を透過した電子をとらえるので、試料の内部状態を観察することができます。例えば、試料が結晶だった場合、その結晶構造を知ることができます。TEMによって得られる結晶構造の情報をシミュレーションで再現してみます。
　今回用いるマルチスライス法というシミュレーション手法では、結晶をいくつかのスライスが重なったものとして、スライスごとに散乱を計算します。まずスライスの二次元的なポテンシャル(投影ポテンシャル)をつくります。次に、投影ポテンシャルを透過した電子の波動関数を計算します。その波動関数を次のスライスへの入射波とします。この流れを繰り返すことで、厚さのある試料の散乱を再現します。スライスする間隔を小さくしていくと、極限で実際の結晶中での散乱と一致します。

プログラム

　投影ポテンシャル$V_p(x, y)$は結晶構造因子$F(h, k, l)$をフーリエ変換して得られます。このとき、結晶構造因子の逆格子点は$l = 0$とします。
$$ F(h, k, l) = \sum_{j=1}^N f_a\exp{\{2\pi i (hx_j + ky_j + lz_j)\}} $$

function crystal_structure_factor(h, k, l, r, invG, param)
        hkl = [h, k, l]
        dk = 1/sqrt(hkl' * invG * hkl)
        sinθλ = 1/(2*dk)

        fa = 0
        for i = 1:4
            fa = fa + param.f[i, 1]*exp(-param.f[i, 2]*sinθλ^2)
        end

        n = size(r)[1]

        F = 0
        for i = 1:n
            F = F + fa*exp(im*2*π*(h*r[i, 1] + k*r[i, 2] + l*r[i, 3]))
        end

        return F, dk
end #crystal_structure_factor

$$ V_p(x, y) = \mathcal{F}[F(h, k, l=0)] $$

using FFTW

h = Vector(-5:0.1:5)
k = Vector(-5:0.1:5)
F = zeros(ComplexF64, length(h), length(k))

for i = 1:length(h), j = 1:length(k)
    F[i, j], dk = crystal_structure_factor(h[i], k[j], 0, r, invG, param)
end

Vp = fftshift(fft(F))

　ちなみに、JuliaではFFTW.jiをuseすることで高速フーリエ変換が行えます。使い方は他の言語のFFTWライブラリと大体同じです。しかし、上のコードのように複素行列をフーリエ変換するときには行列をComplexF64にしておく必要があります。他の複素数型(単なるComplexなど)の行列をフーリエ変換したいのであれば、自分でfft_planを作る必要がありそうです。

　この$V_p$によって散乱された電子の波動関数$\phi$は、位相の変化のみを受けると仮定して
$$ \phi(x, y) = 1 - i\sigma Vp(x, y) $$

これを位相格子q(x, y)としておきます。

function phase_grating(Vp)
	q = ones(ComplexF64, size(Vp))
  q = q .- im*σ.*Vp
    
  return q
end #phase_grating

スライスによって散乱された電子は次のスライスまで真空中を伝播します。真空中での伝播は以下のように表現できます。
$$ P(h, k) = \exp{\{-2\pi i \Delta z \frac{\lambda}{2}[(\frac{h}{a})^2 + (\frac{k}{b})^2]\}} $$

これを伝播関数P(h, k)とします。

function propagation_function(h, k, Δz)
	inexp = -2*π*im*Δz*(diff_param.λ/2)*((h/l_param.a)^2 - (k/l_param.b)^2)
  P = exp(inexp)
    
  return P
end #propagation_function

　これらから、n枚目のスライスを通過した電子線の波動関数は
$$ \phi_{n+1}(x, y) = [\phi_n(x, y)q_n(x, y)]*p(x, y) $$

のように畳み込みの形で表すことができます($*$は畳み込み演算)。この式はフーリエ変換と畳み込みの関係より

$$ \phi_{n+1}(x, y) = \mathcal{F}[\phi_n(x, y)q_n(x, y)]P(h, k) $$

と変形できます。プログラムではこの式をスライス枚数回繰り返します。

　ところで、試料を通過した電子線はそのまま像を形成するのではなく、試料下部にある対物レンズによって焦点に集められることで像を作ります。対物レンズによる球面収差は
$$ \chi(h, k) = \frac{\pi}{2}Cs\lambda^3(h^2 + k^2)^2 + \pi \Delta f \lambda(h^2 + k^2) $$

と表すことができます($Cs$: 球面収差係数, $\Delta f$: デフォーカス量)。

function spherical_aberration(h, k, Cs, λ)
	Δf = 1.2*sqrt(Cs*λ)
  χ = (π/2)*Cs*λ^3*(h^2 + k^2)^2 + π*Δf*λ*(h^2 + k^2)
    
  return χ
end #spherical_aberration

対物レンズによる効果自体は、これもまたフーリエ変換で表すことができ、球面収差の影響を含めて
$$ \exp{\{-i\chi(h, k)\}} $$

となります。これは焦点にできた像なので、実空間でなく逆空間での像(回折パターン)です。さらにこれが電子顕微鏡中で伝播、干渉して焦点の下で実空間像を作ります。計算では逆フーリエ変換をすることに相当します。

　出力された波動関数の絶対値の二乗をとって強度とすることで、像が得られます。この像は結晶内のポテンシャルを反映した像です。

　fccの結晶について実際に行ってみましょう。原子座標は格子定数から対称操作で複製します。具体的には、回転行列と並進ベクトルを用いて変換行列を作り、アフィン変換を行います。原子座標のアフィン変換についてはこの記事を参考にさせていただきました。
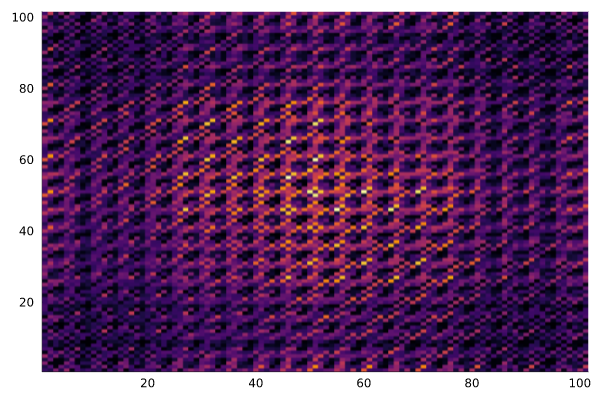
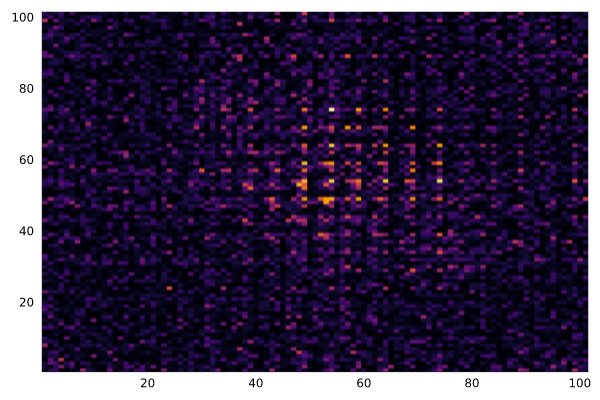
　単位胞16×16×16分の原子座標を計算し、それをもとに指数550反射程度までの結晶構造因子を計算します。結晶構造因子をフーリエ変換して得られた投影ポテンシャルは以下のようになりました。

　投影ポテンシャルから位相格子を作り、別に伝播関数、球面収差を考える指数の範囲において計算しておきます。真空を伝播する距離をc軸の長さの1/2、球面収差係数をとします。デフォーカス量は球面収差係数と電子線の波長から

$$ \Delta f = 1.2\sqrt{Cs\lambda} $$
で得られます(Scherzerフォーカス)。

　マルチスライスのループ計算を行います。一段目のスライスでは入射波は1なので、位相格子がそのまま波動関数となります。それ以降は一段上の波動関数に位相格子をかけたものが波動関数となります。
　波動関数をフーリエ変換して伝播関数をかけ、さらに逆フーリエ変換します。これを下段への入射波とします。
　最終段まで到達したら、球面収差をかけて逆フーリエ変換します。得られた波動関数の絶対値の二乗を取ると強度となり、像が得られます。

for n = 1:repetation
	if n == 1
		ϕn = q
  else
    ϕn = ϕn .* q
  end
  Φn = fft(ϕn)
  Φn1 = Φn .* P
  if n == repetation
	  ϕn = ifft(Φn1 .* exp.(-im.*χ))
  else
    ϕn = ifft(Φn1)
  end
end

投影ポテンシャルをこんな感じにして、実際にやってみましょう。

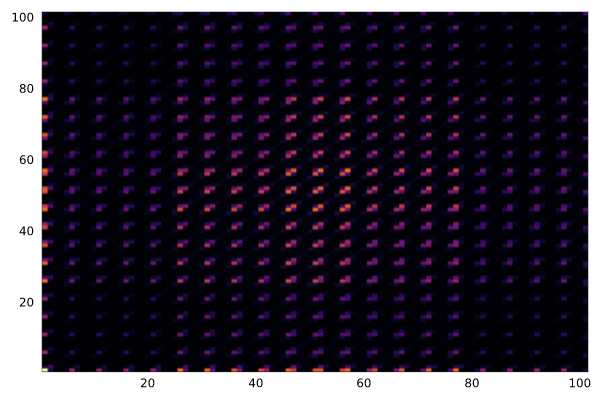
1段のスライスで像は以下のようになりました。投影ポテンシャルをほぼそのまま反映した像が得られています。

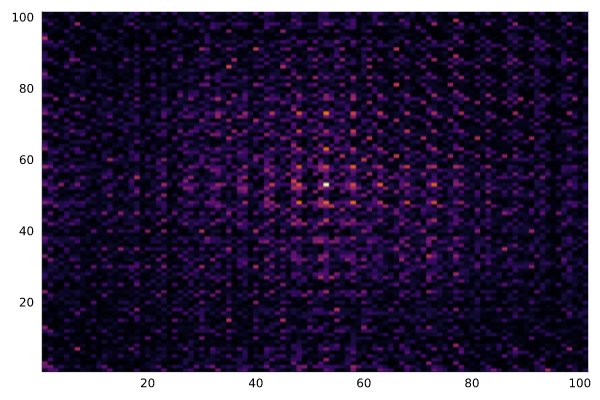
3段、5段のスライスを透過させると以下のようになります。段を重ねるとだんだんとぼやけたようになっています。

まとめ

　以前に似たようなプログラムをPythonで書いたことがありますが、Juliaの方が簡素で速くかけた気がします。ベクトル化せずに繰り返しで行列を作っても速いことが特に大きいです。
　FFTW.jlはFFTWをほぼそのまま移植したものといった感じです。使い方はPythonのscipy.fft()やnumpy.fft.fft()と大体同じですが、上で記したように型が限定されていることに注意が必要です。