投稿日:2021/09/15
更新日:2021/09/29 (単位格子の話を修正)
はじめに
Pythonで結晶を描画するプログラムを作るシリーズの第2回目です。今回はCIFデータ内で使われている分極座標 (fractional coordinate system) (文献によっては原子座標、規格化座標などと呼ばれる)と直交座標系の関係性とその分極座標上のアフィン変換について説明していきます。今回は座学多めで、感覚的に対称操作というものを理解する事を目的とします。
1. 分極座標 (fractional coordinate system)
第1回目の記事でみたように6つの結晶パラメータから大きさや形が異なる単位格子が生成されます。その内、結晶をなすものは7つの晶系に分類され、結晶はそのどれかに必ず分類されます。これらを統一の規格で評価する座標系の1つが分極座標です。分極座標とは単位格子を単位立方体に変換した座標系で単位格子内の相対位置を表します。つまり、単位格子頂点の位置ベクトル$\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}$を変換$F$を用いて
F\boldsymbol{A}=\boldsymbol{a}=\left(\begin{array}{c}
1\\
0\\
0
\end{array}\right), F\boldsymbol{B}=\boldsymbol{b}=\left(\begin{array}{c}
0\\
1\\
0
\end{array}\right),F\boldsymbol{C}=\boldsymbol{c}=\left(\begin{array}{c}
0\\
0\\
1
\end{array}\right)
とした変換した座標系が分極座標系です。ここで、$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$は分極座標系における単位格子頂点の位置ベクトルです。この変換$F$を用いて、単位格子の実際の形を描画する直交座標系(実格子座標系)上の点$\boldsymbol{X}=(X,Y,Z)'$から分極座標上の点$\boldsymbol{x}=(x,y,z)'$への変換は以下のように与えられます:
\boldsymbol{x}=F\boldsymbol{X}=\left(\begin{array}{ccc}
1/A_{x} & -B_{x}C_{z}/V & (B_{x}C_{y}-B_{y}C_{x})/V \\
0 & 1/B_{y} & -A_{x}C_{y}/V \\
0 & 0 & 1/C_{z}
\end{array}\right)\left(\begin{array}{c}
X\\
Y\\
Z
\end{array}\right)\tag{1}
$A_{x},B_{x},\dots,V$の具体的な形は第一回目をご覧ください。この変換$F$は扱う結晶の晶系が立方晶($a=b=c,\alpha=\beta=\gamma=90^\circ$)のとき、
F_{cubic}=\left(\begin{array}{ccc}
1/a & 0 & 0 \\
0 & 1/a & 0\\
0 & 0 & 1/a
\end{array}\right)=\frac{1}{a}I_{3}
です。立方晶の角度は全て$90^\circ$なので単純に各軸に対して規格化を施すというような処理になっているのが見て取れるかと思います。CIFデータに記述される座標情報は全てこの分極座標系で記述されています。つまり、Pythonで結晶を描画するプログラムを作るためにはこの変換の逆変換$F^{-1}$が必要であり、下記のように表されます。
\boldsymbol{X}=F^{-1}\boldsymbol{x}=\left(\begin{array}{ccc}
A_{x} &B_{x} & C_{x} \\
0 & B_{y} & C_{y} \\
0 & 0 & C_{z}
\end{array}\right)\left(\begin{array}{c}
x\\
y\\
z
\end{array}\right)\tag{2}
この変換$F^{-1}$は立方晶のとき、
F_{cubic}^{-1}=\left(\begin{array}{ccc}
a & 0 & 0 \\
0 & a & 0\\
0 & 0 & a
\end{array}\right)=aI_{3}
です。復元するなら各軸を$a$倍しようという事です。これらの変換$F$と$F^{-1}$の間に必ず成り立つ性質として以下があります。
FF^{-1}=F^{-1}F=I_{3}
2. ザイツの記法によるアフィン変換の表現
CIFデータの"_symmetry_equiv_pos_as_xyz"は簡単に言えば分極座標系(xyz)における原子位置が記述されています。厳密な定義については次回取り扱います。[SrTiO3] (https://materialsproject.org/materials/mp-5229/)では下記のように書かれています。
_symmetry_equiv_pos_as_xyz
1 'x, y, z'
2 '-x, -y, -z'
3 '-y, x, z'
4 'y, -x, -z'
5 '-x, -y, z'
6 'x, y, -z'
7 'y, -x, z'
8 '-y, x, -z'
分極座標上の原子位置は上記のように記述されていますが、これはアフィン変換と密接な関わりがあります。アフィン変換とは位置$\boldsymbol{x}=(x,y,z)'$にダミー次元を加えたアフィン空間上の点$\tilde{x}=(x,y,z,1)'$に対する変換であり、この変換をザイツの記法で表記すると以下のように記述されます。
(A|\boldsymbol{b})=\left(\begin{array}{cc}
A & \boldsymbol{b}\\
0 & 1
\end{array}\right)\tag{3}
ここで、$A=(a_{ij})\quad (i,j=1,2,3)$は恒等操作$E$、反転$i$、$n$回回転$C_{n}$、鏡映$\sigma$、回映$S$、回反$C_{\bar{n}}$といった対称操作を表す$3\times 3$行列であり、$\boldsymbol{b}=(b_{i})\quad (i=1,2,3)$は平行移動を表し$3\times 1$の列ベクトルです。この行列$(A|\boldsymbol{b})$は拡大行列とも呼ばれます。$A$と$\boldsymbol{b}$について整理すると、$A$は原点を中心とした変換であり、$\boldsymbol{b}$は原点を移す変換です。例として、$\boldsymbol{x}=(x,y,z)'$を$z$軸の周りに$90^\circ$回転($C_{4}(z)$)させ、$\boldsymbol{b}=(1,1,1)'$と平行移動させる事を考えてみます。まずはザイツの記法を使わすに計算してみます。
\begin{eqnarray}
C_{4}(z)\boldsymbol{x}+\boldsymbol{b}&=&\left(\begin{array}{ccc}
\cos 90^\circ & -\sin 90^\circ & 0\\
\sin90^\circ & \cos 90^\circ & 0 \\
0 & 0 & 1
\end{array}\right)\left(\begin{array}{c}
x\\
y\\
z
\end{array}\right)+\left(\begin{array}{c}
1\\
1\\
1
\end{array}\right)\\
&=& \left(\begin{array}{ccc}
0 & -1 & 0\\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right)\left(\begin{array}{c}
x\\
y\\
z
\end{array}\right)+\left(\begin{array}{c}
1\\
1\\
1
\end{array}\right)\\
&=& \left(\begin{array}{c}
-y+1\\
x+1\\
z+1
\end{array}\right)
\end{eqnarray}
これより、$\boldsymbol{x}=(x,y,z)'$は$\boldsymbol{x}'=(-y+1,x+1,z+1)'$に移動する事がわかります。ザイツの記法では計算すると以下が得られます。
\begin{eqnarray}
\left(\begin{array}{cc}
C_{4}(z) & \boldsymbol{b}\\
0 & 1
\end{array}\right)\tilde{x}&=&\left(\begin{array}{cccc}
\cos 90^\circ & -\sin 90^\circ & 0 & 1\\
\sin90^\circ & \cos 90^\circ & 0 & 1\\
0 & 0 & 1 & 1\\
0 & 0 & 0 & 1
\end{array}\right)\left(\begin{array}{c}
x\\
y\\
z\\
1
\end{array}\right)\\
&=& \left(\begin{array}{c}
-y+1\\
x+1\\
z+1\\
1
\end{array}\right)
\end{eqnarray}
この記法でも同様の点に移動している事がわかります。ザイツの記法のおいしい点は対称操作と平行移動を含めた操作を1つの線形変換のように取り扱える事にあります。さらにダミー次元はどんな変換を考えても必ず$1$になるので計算結果からこの次元を除けば直ぐにどの点に移動したかわかります。ただし、この計算結果は結晶学において素直に受け取ってはいけないもので、計算結果について考える必要があります。そのためにいくつかの数学的な準備をします。実格子座標系における単位格子の頂点$\boldsymbol{r}$は整数$r_1,r_2,r_3$を用いて、
\boldsymbol{r} = r_{1}\boldsymbol{A}+r_{2}\boldsymbol{B}+r_{3}\boldsymbol{C}:= (r_{1},r_{2},r_{3})_{r}
と表現する事にします。また、分極座標系における単位格子の頂点$\boldsymbol{p}$は整数$n_{1},n_{2},n_{3}$を用いて、
\boldsymbol{p} = n_{1}\boldsymbol{a}+n_{2}\boldsymbol{b}+n_{3}\boldsymbol{c}:= (n_{1},n_{2},n_{3})_{p}
と記述する事にします。このとき、$(n_1,n_2,n_3+1)_ x$,$(n_1,n_2+1,n_3)_ x$,$(n_1+1,n_2,n_3)_ x$,$(n_1+1,n_2+1,n_3)_ x$,$(n_1,n_2+1,n_3+1)_ x$,$(n_1+1,n_2,n_3+1)_ x$,$(n_1,n_2+1,n_3+1)_ x$,$(n_1+1,n_2+1,n_3+1)_ x$の8つの頂点に囲まれた領域において$x=r$のとき$U_{n_1 n_2 n_3}^{(r)}$、$x=p$のとき$U_{n_1 n_2 n_3}^{(p)}$と書くことにします。特に上または下の添え字を省略したときは$p$にも$r$にも言える事とします。また、"$U_{xyz}$の原点から"と記述した場合、"$(x,y,z)$から"を意味する事にします。このように書き直したとき、$U_{n_1 n_2 n_3}^{(r)}$内の原子位置は変換$F$によって$U_{n_1 n_2 n_3}^{(p)}$の領域に写像したといえます。ここで大前提として結晶は長距離的な秩序が保たれる必要があるので、$U_{xyz}$の原点から位置$\boldsymbol{x}$に存在する原子は必ず$U_{x'y'z'}$の原点から位置$\boldsymbol{x}$に存在します。これらを使って計算結果の解釈を行いたいと思います。$U_{xyz}^{(p)}$上の原子に対するアフィン変換で$U_{x'y'z'}^{(p)}$の領域に移ったとします。この原子が$U_{x'y'z'}^{(p)}$の原点から$\boldsymbol{v}$にあるとき、結晶の性質から$U_{x'y'z'}^{(p)}$の原点から$\boldsymbol{v}$に原子が存在する必要があります。このように考えたとき、$U_{000}$の領域中の点$(x,y,z)'$は$U_{klm}$の原点から$(x,y,z)'$に位置に存在し、原点$(0,0,0)'$から見ると$(k+x,l+y,m+z)'$に位置する事になります。単位格子の議論において、基本的にどこか1つの領域に絞って考えれば良いので、$U_{000}$に注目すると$(x,y,z)'=(k+x,l+y,m+z)'$と考えても良い事がわかります。つまり、$\boldsymbol{x'}=(-y+1,x+1,z+1)'$は$U_{111}$の原点から$(-y,x,z)'$に位置に存在する事を意味しています。ただ、前述しよたように原点を変えただけの同一点であるため、ユニークな位置とは言えません。これをCIFの"_symmetry_equiv_pos_as_xyz"に書くのであれば下記になります(これを要素に持つ空間群はないのであくまでも例だと考えて下さい)。
_symmetry_equiv_pos_as_xyz
1 'x, y, z'
2 '-y, x, z'
ここでしっかり押さえておきたいのが、$U_{xyz}$にある点は$U_{x'y'z'}$にも存在するという制限を満たすアフィン変換のみがその結晶の変換操作の元になるという事です。そして、この元による分類を結晶に施していくと230種類の空間群に分類できるという話につながっていきます。結晶においてという前置きをしましたが、たんぱく質結晶はL-アミノ酸の性質上65種類とさらに絞られるようです[1]。余談ですがニューラルネットワークなどはアフィン変換や活性化関数などを組み合わせたものであるため、ザイツの記法を使うとよりシンプルに表現できます。
3. 任意の軸周りの回転
ザイツの記法による拡大行列を構成する要素は前述したように対称操作$A$と平行移動$b$です。ここでは対称操作$A$における回転$C_{n}$について取り扱っていきます。ここで、$C_{n}$は$\theta\left(=\frac{2\pi}{n}\right)$回転を表します。結晶では$n=2,3,4,6$のみ考えれば良いのですが、ここでは任意回転軸における$\theta [rad]$回転として取り扱います。
ロドリゲスの回転公式 (Rodrigues' rotation formula)
任意の単位回転軸ベクトル$\boldsymbol{p}=(p_1,p_2,p_3)'$まわりに$\theta$回転させる回転行列$R_{p}(\theta)$は
R_{p}(\theta)=
\left(\begin{array}{ccc}
c + p_{1}^2(1-c) & p_{1}p_{2}(1-c)-p_{3}s & p_{1}p_{3}(1-c)+ p_{2}s \\
p_1 p_2 (1-c)+p_3 s & c+p_2^2 (1-c) & p_2 p_3 (1-c) -p_1 s \\
p_1 p_3(1-c)-p_2 s & p_2 p_3 (1-c)+ p_1 s & c + p_3^2 (1-c)
\end{array}\right)
である。ここで、$s=\sin\theta,c=\cos\theta$を表す。
特に、$p=(0,0,1)'$かつ$\theta = 90^\circ$のとき、$R_{p}(90^\circ)=C_{4}(z)$です。
ここまでの勉強した所を使って点の移動の軌跡をみるプログラムを作っていきましょう。まず、注意点としてmathライブラリにおける三角関数は誤差が出てしまうという事が挙げられます。例えば、$\cos(\pi/2)=0$という関係を素直にコードで書けば"math.cos(math.pi/2)"なのですが、出力結果は6.123233995736766e-17です。非常に小さな桁で誤差が出るため、厳密な$0$になりません。簡単な対処法は出力結果を四捨五入して$0$とするという方法です。そもそも、小数点十数位の変化がピクセルをまたいで変化して見える事がないので適当な桁で処理してしまうのが良いかと思います。また、numpyは1次元配列はベクトルの転置をとったものになっているので、行列積を考えるときは転置".T"をとる必要があります。これらを踏まえて、ロドリゲスの回転公式に代入しこの回転行列と平行移動ベクトルから式(3)の拡大行列を出力、この行列と移動させたい点の行列積を計算し、移動先の点を求め、図示という手順で処理していきたいと思います。
import numpy as np
import math
from decimal import Decimal, ROUND_HALF_UP
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 関数
def deg2rad(deg):
"""
deg→rad
"""
return deg*(math.pi/180)
def Round(vec,digit):
"""
入力された値をdigitsの桁で四捨五入する
"""
num = len(vec)
Rounding = []
for i in range(num):
a = Decimal(str(vec[i])).quantize(Decimal(digit),rounding=ROUND_HALF_UP)
a = float(a)
Rounding.append(a)
return Rounding
def Rodrigues(vecP,theta,digit='0.01'):
"""
ロドリゲスの回転行列。
------------------------------
vecP : array-like
回転軸を表すベクトル
theta : float
反時計周りにθ回転させる。θはdegreeで入力する。
"""
theta = deg2rad(theta)
p1,p2,p3 = vecP
c = math.cos(theta)
s = math.sin(theta)
# 回転行列の成分
R11 = c+(1-c)*p1**2
R12 = p1*p2*(1-c)-p3*s
R13 = p1*p3*(1-c)+p2*s
R21 = p1*p2*(1-c)+p3*s
R22 = c+(1-c)*p2**2
R23 = p2*p3*(1-c)-p1*s
R31 = p1*p3*(1-c)-p2*s
R32 = p2*p3*(1-c)+p1*s
R33 = c+(1-c)*p3**2
return np.array([Round([R11,R12,R13],digit)
,Round([R21,R22,R23],digit)
,Round([R31,R32,R33],digit)])+0
def seitzMtx(mtx,vecB):
"""
ザイツの記法による拡大行列。
---------------------------------
mtx:array
3×3の行列
vecB:array-like
平行移動を表すベクトル
"""
seitzMtx = np.insert(mtx,3,vecB,axis=1) # 4列目にvecBを加える
seitzMtx = np.insert(seitzMtx,3,[0,0,0,1],axis=0) # 4行目に[0,0,0,1]を加える
return seitzMtx
def movePos(seitzMtx,x):
"""
ザイツ記法の拡大行列とxの行列積。
-----------------------------------
x:array-like
xは実格子上の点とする
"""
xtilde = np.insert(x,3,1,axis=0).T # (x,y,z)→(x,y,z,1)
return np.dot(seitzMtx,xtilde)
def drawCircle(x_bef,vecP):
"""
rotMtxが回転する平面の図示。
"""
p1,p2,p3 = vecP
Theta = [i for i in range(0,360,1)]
x = np.zeros(len(Theta))
y = np.zeros(len(Theta))
z = np.zeros(len(Theta))
vecP_unit = np.array([p1,p2,p3])/math.sqrt(p1**2+p2**2+p3**2) # vecPを単位ベクトルに変換
xc,yc,zc = np.dot(np.array(x_bef).T,vecP_unit.T)*vecP_unit # x_befからvecPの線上に垂直におろした点(xc,yc,zc)
for i,theta in enumerate(Theta):
x[i],y[i],z[i] = np.dot(Rodrigues(vecP_unit,theta),np.array(x_bef).T)
return x,y,z,xc,yc,zc
def Mysimulation(x_bef,vecP,vecB,theta,size=40,fontsize=15,fig_size1=8,fig_size2=8,color='r',arrow_length_ratio=0.1,lim=8):
"""
pos_bftからpos_aftに向かう矢印、x,y,z軸の描画
"""
# ●計算
rotMtx = Rodrigues(vecP,theta)
seitz = seitzMtx(rotMtx,vecB)
x_aft = movePos(seitz,x_bef)[:-1] # 末尾はダミー次元なので使わない
# ●描画
fig = plt.figure(figsize=(fig_size1,fig_size2))
ax = fig.add_subplot(111,projection='3d')
# 移動前と移動後の点のプロットおよびその間に矢印を引く
x,y,z = x_bef
u,v,w = x_aft
p1,p2,p3 = vecP
ax.quiver(x,y,z,u-x,v-y,w-z,color=color,arrow_length_ratio=arrow_length_ratio)
ax.scatter(x,y,z,color='b',s=size)
ax.text(x,y,z,s=r'$x_{bft}$',fontsize=fontsize)
ax.scatter(u,v,w,color='r',s=size)
ax.text(u,v,w,s=r'$x_{aft}$',fontsize=fontsize)
# x,y,z軸の追加
ax.quiver(-lim,0,0,2*lim,0,0,linestyle='-', arrow_length_ratio=0.1,color='black') # x軸
ax.quiver(0,-lim,0,0,2*lim,0,linestyle='-', arrow_length_ratio=0.1,color='black') # y軸
ax.quiver(0,0,-lim,0,0,2*lim,linestyle='-', arrow_length_ratio=0.1,color='black') # z軸
# x_befが回転する平面
ax.quiver(-lim*p1,-lim*p2,-lim*p3,2*lim*p1,2*lim*p2,2*lim*p3,linestyle='--', arrow_length_ratio=0.1,color='b') # 回転軸
r1,r2,r3,xc,yc,zc = drawCircle(x_bef,vecP) # x_befが回転する平面
ax.plot(r1,r2,r3,color='g',ls='--')
ax.quiver(xc,yc,zc,x-xc,y-yc,z-zc,linestyle='-', arrow_length_ratio=0.1,color='g')
# x_befの回転先
xr,yr,zr = np.dot(rotMtx,np.array(x_bef).T)
ax.scatter(xr,yr,zr,color='g',s=size)
ax.quiver(xc,yc,zc,xr-xc,yr-yc,zr-zc,linestyle='-', arrow_length_ratio=0.1,color='g')
ax.quiver(x,y,z,xr-x,yr-y,zr-z,linestyle='--', arrow_length_ratio=0.1,color='r')
ax.text(xr,yr,zr,s=r'$x_{rot}$',fontsize=fontsize)
# 回転先から移動後のプロットまでに矢印を引く
ax.quiver(xr,yr,zr,u-xr,v-yr,w-zr,linestyle='--', arrow_length_ratio=0.1,color='r')
# 出力範囲
ax.set_xlim(-lim,lim)
ax.set_ylim(-lim,lim)
ax.set_zlim(-lim,lim)
# 軸ラベル
ax.set_xlabel('x',size=14)
ax.set_ylabel('y',size=14)
ax.set_zlabel('z',size=14)
return rotMtx,seitz,x_aft
# 回転軸ベクトルP, 点x, 平行移動vecB, 回転角thetaの指定
vecP = [0,0,1] # z軸
x_bef = [-0.5,-0.5,-1]
vecB = [1,1,1] # b=(1,1,1)'の移動
theta = 90
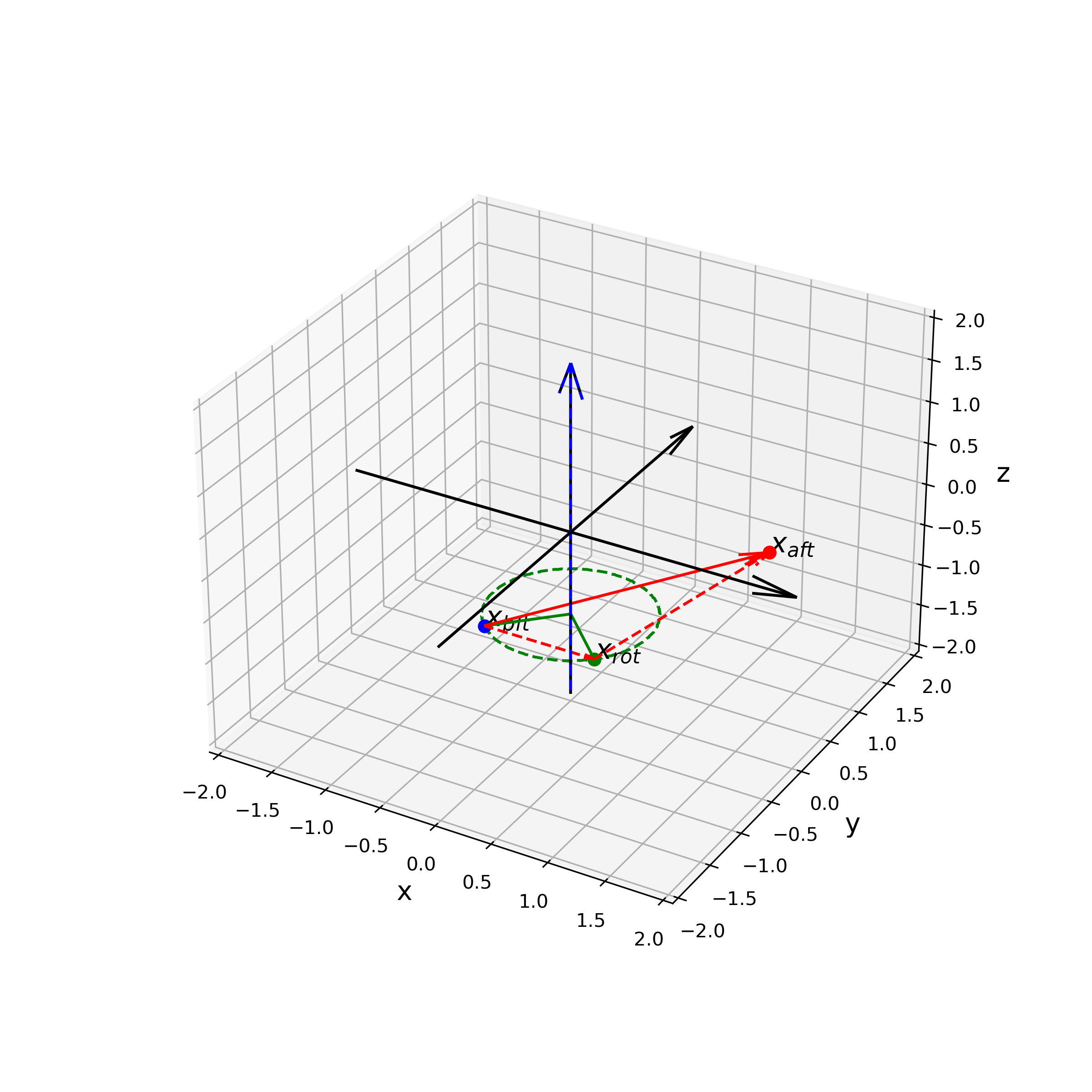
_,_,_ = Mysimulation(x_bef,vecP,vecB,theta,lim=2)
# plt.savefig('test.png',transparent=True,dpi=300)
Rodrigues関数の戻り値に$+0$を付けているは、$-0$が配列の成分として出力される事がありこれを$0$に直すためです。今回は$-0$が出力されても影響はないのですが、この値を使って"math.acos"などを実行すると期待しない結果が得られます。drawCircle関数は入力された点$x$("x_bef")がどのような円周上で回転しているのかをみるための処理になっており、点$x$が360度回転したときの軌跡をfor文で計算しています。そのためには、点$x$から回転軸上に垂直におろした点を算出する必要があります。この算出方法はベクトル解析の知識を使っています。回転軸のベクトル$\boldsymbol{P}=(p_{1},p_{2},p_{3})'$("vecP")から同じ方向を向く単位ベクトル$\boldsymbol{e_{p}}$("vecP_unit")を
\boldsymbol{e_{p}}=\frac{\boldsymbol{P}}{||\boldsymbol{P}||_{2}}
で計算します。これを用いると、点$x$を回転軸上に垂直におろした点$P_{0}$は
\boldsymbol{P}_{0}=(\boldsymbol{x}\cdot\boldsymbol{e_{p}})\boldsymbol{e_{p}}
によって求まります。この関係を利用して"xc,yc,zc"を算出しています。
上記を実行すると以下の図が得られます。今回は対称操作の1つである回転に限ってのプログラムを作成しましたが、seitzMtx関数の引数である"mtx"に恒等操作$E$、反転$i$、鏡映$\sigma$、回映$S$、回反$C_{\bar{n}}$を表す$3\times 3$行列を代入する事で様々な操作による変化を楽しむことができます。
最後に複数の点が対称操作と平行移動によってどう変化するのかを描画するプログラムを作成して終了したいと思います。
def movePoss(seitzMtx,pSet_bef):
"""
点集合pSet_befをseitzMtxによってpSet_aftに移す
-----------------------------------
pSet:array
点集合の座標
"""
num = pSet_bef.shape[1]
pSet_aft = np.zeros_like(pSet_bef)
for i in range(num):
xtilde = np.insert(pSet_bef[:,i],3,1,axis=0).T
pSet_aft[:,i] = np.dot(seitzMtx,xtilde)[:-1]
return pSet_aft
def Mysimulation2(vecP,vecB,pSet_bef,theta,size=40,fontsize=15,fig_size1=8,fig_size2=8,color='r',arrow_length_ratio=0.1,lim=8):
"""
pSet_bef, pSet_aftの描画
"""
# ●計算
rotMtx = Rodrigues(vecP,theta)
seitz = seitzMtx(rotMtx,vecB)
seitz_rot = seitzMtx(rotMtx,[0,0,0]) # 回転のみ
seitz_trans = seitzMtx(np.eye(3),vecB) # 平行移動のみ
pSet_rot = movePoss(seitz_rot,pSet_bef)
pSet_trans = movePoss(seitz_trans,pSet_bef)
pSet_aft = movePoss(seitz,pSet_bef)
# ●描画
fig = plt.figure(figsize=(fig_size1,fig_size2))
ax = fig.add_subplot(111,projection='3d')
# 移動前と移動後の点のプロット
ax.scatter(pSet_bef[0],pSet_bef[1],pSet_bef[2],color='b',s=size,label=r'$x_{bef}$')
ax.scatter(pSet_trans[0],pSet_trans[1],pSet_trans[2],color='g',s=size,label=r'$x_{trans}$')
ax.scatter(pSet_rot[0],pSet_rot[1],pSet_rot[2],color='c',s=size,label=r'$x_{rot}$')
ax.scatter(pSet_aft[0],pSet_aft[1],pSet_aft[2],color='r',s=size,label=r'$x_{aft}$')
# x,y,z軸の追加
ax.quiver(-lim,0,0,2*lim,0,0,linestyle='-', arrow_length_ratio=0.1,color='black') # x軸
ax.quiver(0,-lim,0,0,2*lim,0,linestyle='-', arrow_length_ratio=0.1,color='black') # y軸
ax.quiver(0,0,-lim,0,0,2*lim,linestyle='-', arrow_length_ratio=0.1,color='black') # z軸
# 回転軸
p1,p2,p3 = vecP
ax.quiver(-lim*p1,-lim*p2,-lim*p3,2*lim*p1,2*lim*p2,2*lim*p3,linestyle='--', arrow_length_ratio=0.1,color='b')
# 出力範囲
ax.set_xlim(-lim,lim)
ax.set_ylim(-lim,lim)
ax.set_zlim(-lim,lim)
# 軸ラベル
ax.set_xlabel('x',size=14)
ax.set_ylabel('y',size=14)
ax.set_zlabel('z',size=14)
plt.legend()
return rotMtx,seitz,pSet_aft
# 単位格子内の点集合を乱数で生成
np.random.seed(1) # シード値の固定
points = 20 # 生成する点の数
x = np.random.rand(points) # x座標
y = np.random.rand(points) # y座標
z = np.random.rand(points) # z座標
pSet_bef = np.array([x,y,z])
# 回転軸ベクトルP,平行移動vecB, 回転角thetaの指定
vecP = [0,0,1]
vecB = [-1,-1,-1]
theta = 90
# 描画
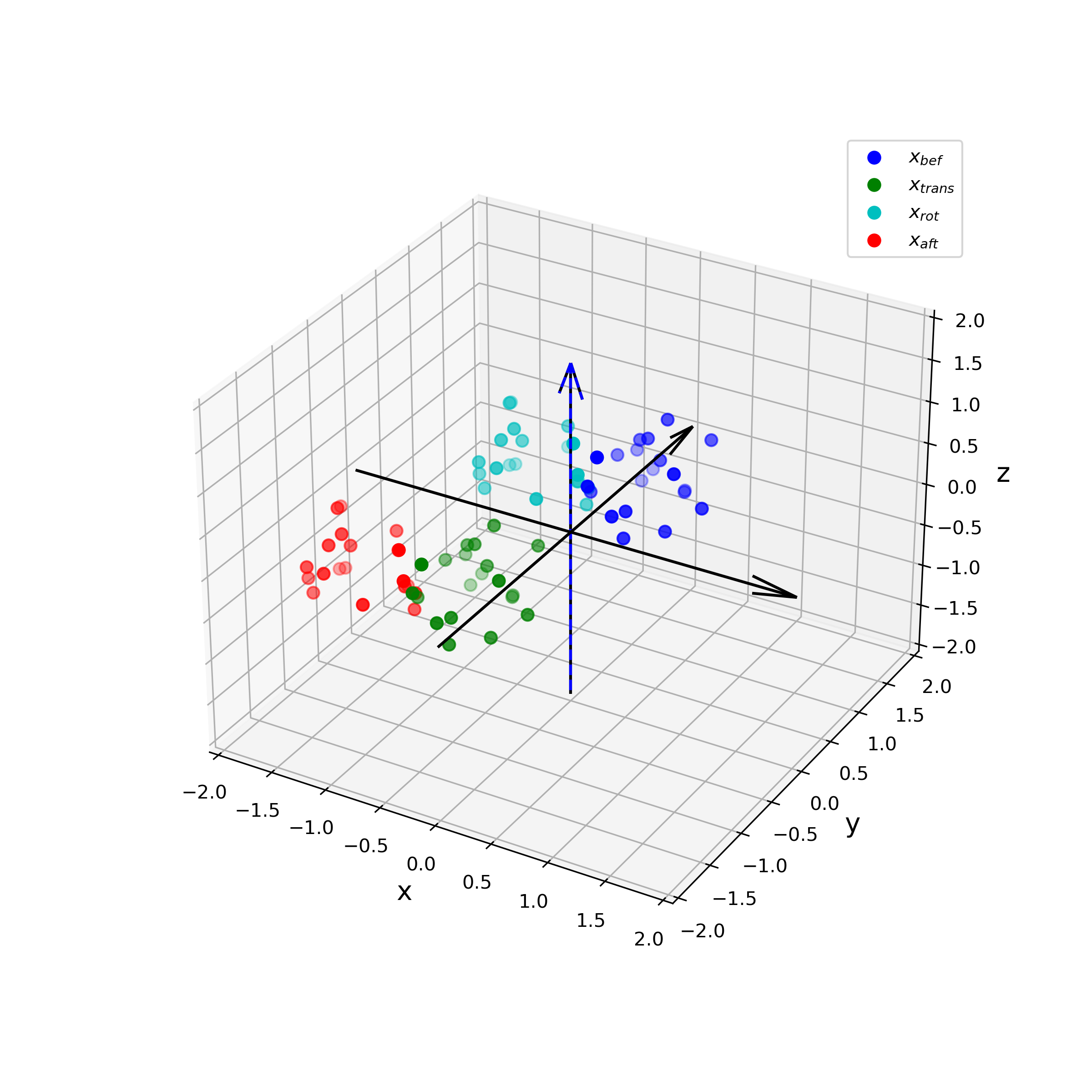
_,_,_=Mysimulation2(vecP,vecB,pSet_bef,theta,lim=2)
# plt.savefig('test2.png',transparent=True,dpi=300)
上記のプログラムを実行する下図が得られます。この例では点の集合を乱数で作成していますが、前の記事扱った平行六面体の頂点に実行してみて下さい。
参考文献
[1] S. Fushinobu, タンパク質結晶のとりうる空間群の表, 2007. http://enzyme13.bt.a.u-tokyo.ac.jp/sgroup.html