fukuoka.ex & 福岡 理学部の piacere です
ご覧いただいて、ありがとうございます ![]()
「重力プログラマの理論物理学」を重力プログラミング入門に足そうと思います![]()
ちなみに、これまでの重力プログラミング入門は、以下の通りです
|> 「第1回:地球の重力下で人工衛星を公転軌道に乗せる」
|> 「第2回:Pythonで重力波を解析する」 ※登壇向けスライド版もあります
|> 「第3回:太陽フレアをディープラーニングで予測する」
|> 「第4回:スペースコロニーを建造する」
|> 「第5回:ブラックホールを流体力学+Unityでシミュレーションする」 ※資料未公開
|> 「第6回:惑星の位置・軌道を計算する」


 5/24(金)にこのコラムに連動した登壇します
5/24(金)にこのコラムに連動した登壇します 


5/24(金)に天神で開催する「福岡 理学部 12限目」にて、「数字や機械学習が苦手でもブラックホールが理解できる相対性理論のススメ」というテーマで、このコラム+αの登壇しますので、遊びに来てください
なお、LT枠も、絶賛募集中です
募集しているLTは、数学的興味や、知的好奇心、探求心を満たす集まりで、「理学であれば、テーマはなんだって自由」という、フリーダム(私みたいに重力や宇宙で無くてもOK)![]()
レベル感も、入門編からマニアックなものまで、やはりフリーダムなので、どうぞLTトライしてください(ここも私みたいに数式バリバリとかで無くてOK) ![]()
いずれの参加申し込みも、下記をクリックしてください
万有引力
まさかの 10,000 PV/100いいね を越え、2017年12月には登壇も行った、重力プログラミング入門「第2回:Pythonで重力波を解析する」でも紹介していますが、重力のスタート地点は、ニュートンが1687年にまとめた「万有引力」です
2つの物体の間に働く重力を、以下の式で表しますが、この重力は、2つの物体の「質量」と「距離(半径)」で表します
F = G\frac{Mm}{r^2}
- G:重力定数
- M、m:2点の各質量
- r:半径
なお、天文学や宇宙開発では、「重力」≒「万有引力」として扱っており、本来、重力を構成する「自転による遠心力」は省略されるようです(以降でも省略します)
重力場
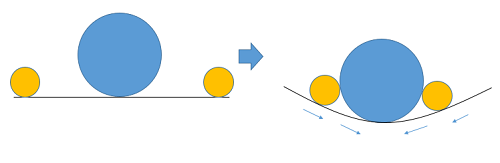
さて、この万有引力において、下記イメージの「惑星」と「人工衛星」のような、質量差があまりに大き過ぎる場合、大質量側を「重力源」と置き、この重力源が発生させる「重力場」として表現します
重力場は、以下のような、小質量側の m が無視され、大質量側の M のみの式となります
g=-G\frac{M}{r^2}
自由落下速度
2017年9月の公開から、2,000名以上の読者に読まれた、重力プログラミング入門「第1回:地球の重力下で人工衛星を公転軌道に乗せる」のP24で説明していますが、人工衛星が地球の周りを回り続けるのは、地球方向への「自由落下速度」で落ち続けているけど、同時に地球方向と直角に、地表へ落ちないだけの「第1宇宙速度」で水平移動しているからです
このときの自由落下速度は、以下の式で表します
v=\sqrt{2GM/r}
- G:重力定数
- M:質量
- r:半径
この式では、半径 r が小さくなるほど、つまり、中心に向かうほど落下速度は増大します
シュバルツシルト半径…それは光さえ届かないもの
地球のような、中心が鉱物で構成される物体では、地表に邪魔されるため、半径 r が小さくなるにも限界があり、落下速度も自ずと限界があるのですが、木星のような、中心がガスで構成される物体を仮定すると、地表に邪魔されず、半径が小さくなるので、落下速度が、速度の上限である「光の速度 c」を越えてしまい、上記の自由落下速度の式は破綻します
この破綻の境界となる半径を「シュバルツシルト半径」と呼び、下記式で表されます
Rs=\frac{2GM}{c^2}=2.9 (\frac{M}{M_⦿})[km]
- c:光の速度(≒秒速30万km)
式を見ても分かる通り、重力源の質量が大きくなればなるほど、この半径は、大きくなります
地球(と同等質量の地表が無い惑星)のシュバルツシルト半径
地球質量(≒5.974 × 10^24 kg、約5,974,000,000,000,000,000,000 トン)かつ地表が無かった場合、光の速度 c に到達するシュバルツシルト半径は、約0.9cmと、実はかなり小さいです
木星のシュバルツシルト半径
当然、地球より質量の大きい木星(≒1.898 × 10^27 kg、約1,898,000,000,000,000,000,000,000 トン)
)では、この半径はもっと大きくなるのですが、木星のシュバルツシルト半径でさえ、約2.82mと、かなり小さな半径になります
太陽のシュバルツシルト半径
これが太陽(≒1.989 × 10^30 kg、約1,989,000,000,000,000,000,000,000,000 トン)だと、295,500m、つまり、295.5kmになります … 太陽がいかに質量/重力ともに巨大な天体かが分かります
「光の速度 c」と「重力」を統合する「一般相対論」
さて、各質量毎のシュバルツシルト半径 Rs よりも、半径 r が小さくなると、光の速度 c を越えてしまい、自由落下速度の式が破綻することが分かりました
この状況を正確に扱えるようになったのは、1916年、アインシュタインが発表した「一般相対性理論」、略して「一般相対論」が登場してからです
この一般相対論の基本となる「アインシュタイン方程式」により、「重力」と「運動方程式」が統合されました
アインシュタイン方程式は、以下の式です(今回コラムで扱わず、紹介だけなので、未だ理解しなくてOK)
G_{μν}=\frac{8πG}{c^4}T_{μν}
- Gμν:「アインシュタイン・テンソル」= 時空の曲がり具合
- G:重力定数 ※万有引力の法則のGと同じ
- c:光の速度
- Tμν:「エネルギー・運動量テンソル」= 質量・エネルギーの密度と流れを表すもの
「重力場」の解釈が変わる
アインシュタイン方程式によると、「重力場」は、「物質もしくはエネルギーが存在することで、時間/空間が歪む効果」として解釈されます
平たく言うと、重力とは、ある物体が質量により時空(≒3次元空間に時間を加えた概念)を歪めたことで、もう一方の物体が、歪んだ方向に転がっていく現象である、ということで、こうした現象が発生する場を、重力場と呼ぶ訳です
重力で時間経過が変わる「シュバルツシルト解」
「一般相対論」を導入することで、落下速度の、光の速度 c までの到達には、「重力」と、それに伴う「時空への影響」を加えることができ、下記の式で表される「シュバルツシルト解」が考案されました
dτ=(1-\frac{Rs}{r})^{1/2}dt
- r:半径
- Rs:シュバルツシルト半径
- dτ:任意の位置における時間間隔
- dt:無限遠方の観測者における時間間隔
この解から、「半径 r がシュバルツシルト半径 Rs に近づくと、dt が相対的に大きくなる … つまり「時間経過」が遅くなり、落下速度は、いつまでも c を超えない」という解釈ができるようになりました
一方、シュバルツシルト半径 Rs の外側から見ると、半径内での「時間経過」が遅くなったことで、物体の移動がまるで止まったかのようになります
「ブラックホールに落ちた人を、外から見ると、止まったように見える」という説は、ここから説明できます

こうした、場所によって経過する時間が異なることを、「固有時」と言います
オマケ:「シュバルツシルト解」における条件
なお、シュバルツシルト解は、「中心のみに質点が存在し、その周囲の空間は等方的※である」という条件を導入しています
※等方的(と異方的)
等方的(isotropic):ある対象の性質や分布が方向に依存しない(回転により変化しない)
異方的(anisotropic):方向に依存する(回転により変化する)
「事象の地平線」、そしてブラックホール
シュバルツシルト解によると、半径 r が、シュバルツシルト半径 Rs より内側に入った場合、(光の速度 c を超える脱出速度が無い限り)外側には出られなくなることを意味します
物体や世界の動きは、光が反射することで見える訳なので、シュバルツシルト半径 Rs より内側の世界は、外側から見ることができなくなります
ここから、シュバルツシルト半径 Rs のことを「事象の地平線」と呼びます
そして、この「事象の地平線」と、上記した「中心のみに質点が存在する」を併せた概念のことを、「ブラックホール」と呼びます

ブラックホールは、最初、このような理論上の仮説からスタートしたのです
そして、その後、惑星・恒星に対する理解が深まり、大質量恒星が時間経過すると、中心部が高密度になることが分かり、更に自重力で潰れ、シュバルツシルト半径より小さくなり、ブラックホールが実在する可能性に至ったのです
終わり
重力の基礎である「万有引力」からスタートし、ブラックホールまで至る、今回のコラム、いかがでしたでしょうか?
ブラックホールや「事象の地平線」といった事象・概念が、重力と半径、そして時間経過といった「数式」として理解でき、それらの増減が数式からイメージできるようになったら、とても嬉しいです![]()