MLPシリーズで最近話題の『ガウス過程と機械学習』を読みました。ガウス過程について勉強するのは初めてだったのですが、とても丁寧で分かりやく、最後まで読み通すことができました。
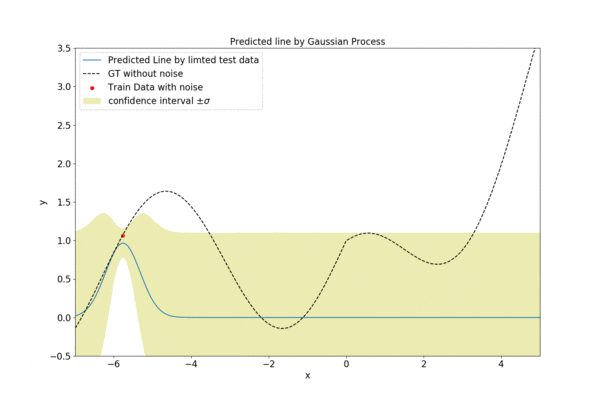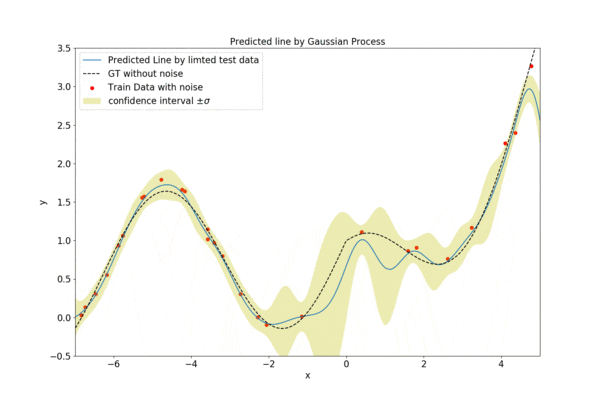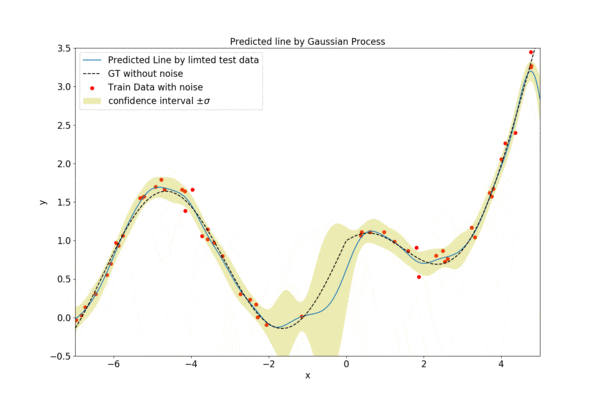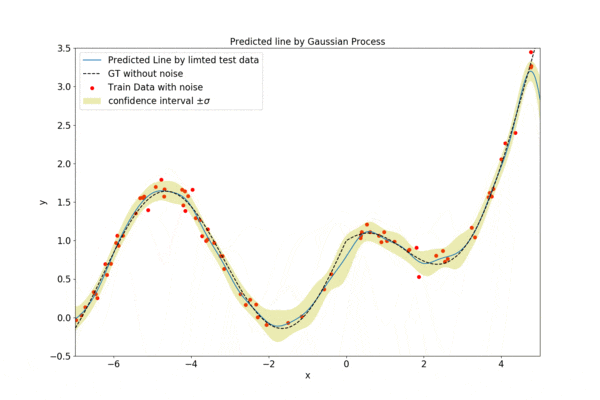
3.4節の図3.16を再現すべく、pythonで1次元ガウス過程回帰を実装しました。全コードはgitにあげました。
記号の使い方
小文字の太字は縦ベクトル、大文字の太字は行列は表します。行列$\boldsymbol{A}$の$i,j$成分を$\boldsymbol{A}_{i,j}$と書きます。
多次元ガウス分布
$D$次元ガウス分布を、平均パラメータベクトル$\boldsymbol{\mu}\in \mathbb{R}^D$, 共分散行列${\bf \Sigma}\in \mathbb{R}^{D \times D}$を用いて
$$
{\mathcal N}({\bf x}|\boldsymbol{\mu},{\bf \Sigma})=\frac{1}{\sqrt{(2\pi)^D|{\bf \Sigma}|}} {\rm exp} \left\{ -\frac{1}{2}({\bf x}-\boldsymbol{\mu})^{\rm T}{\bf \Sigma^{-1}({\bf x}- \boldsymbol \mu)} \right\}
$$
で定義します。
理論
詳細は『ガウス過程と機械学習』の第3章を読んでください。ここでは、結論を書くに留めます。
訓練データ集合$D=\{(x_i, y_i) | i = 1,\cdots, N \}$ はある連続な関数$f(x)$から観測された点の集合です。観測に伴いノイズを拾い、$y_i$は真の値よりもややずれた値を持つとします。このノイズは真の値を中心としたガウス分布に従って発生するとします。また、$\boldsymbol y = (y_1, \cdots, y_N)^{\rm T}$とします。
ここで集合$\boldsymbol{X}^{*}=(x_1^{*},\cdots,x_M^{*})$の各要素を関数$f(x)$に入力した場合に予測される出力値$\boldsymbol{y}^{*}=(y_1^{*},\cdots,y_M^{*})^{\rm T}$は、
$$
p(\boldsymbol{y}^{*}|\boldsymbol{X}^{*},D) = {\mathcal N}({\boldsymbol y^*}|\bf k_*^{\rm T} \bf K^{\rm -1} \boldsymbol y \rm , \bf k_{**} - \bf k_*^{\rm T} \bf K^{\rm -1} \bf k_*)
$$
に従います。ただし、ここで、$\bf{ K} \in \mathbb{R}^{\rm N×N}, \bf k_* \in \mathbb{R}^{\rm N×M}, \bf k_{**} \in \mathbb{R}^{\rm M×M}$であり、各々の要素はカーネル関数$k(\cdot,\cdot)$を用いて
{\bf K}_{n,n'} = k (x_n,x_{n'}) \\
{\bf k_*}_{n,m} = k (x_n,x^*_{m}) \\
{\bf k_{**}}_{m,m'} = k (x^*_m,x^*_{m'})
と書けます。この記事ではカーネル関数をRBFカーネルにノイズの効果を足した
k (x_p,x_q) = \theta_1 {\rm exp}\left(-\frac{|x_p-x_q|^2}{\theta_2}\right) + \theta_3\delta(x_p,x_q)
とします。ここで$\delta(x_p,x_q)$は$x_p=x_q$で1、それ以外で0をとる関数です。$\theta_1,\theta_2,\theta_3$はハイパーパラメータです。
実装
まず、データ集合$D$や$\boldsymbol{X}^{*}$をつくるクラスを用意します。
import numpy as np
import matplotlib.pyplot as plt
import math
class DataSet:
def __init__(self, xmin, xmax, num_data, noise_level):
self.xmin = xmin
self.xmax = xmax
self.x = (xmax - xmin) * np.random.rand(num_data) + xmin
self.x = np.sort(self.x)
self.y = np.empty(num_data)
for i in range(num_data):
self.y[i] = self.make_y(self.x[i], noise_level)
@staticmethod
def make_y(x, noise_level):
if x > 0:
return 1.0/2.0*x**(1.2) + math.cos(x) + np.random.normal(0, noise_level)
else:
return math.sin(x) + 1.1**x + np.random.normal(0, noise_level)
def plot(self):
plt.figure(figsize=(15, 10))
plt.xlabel("x", fontsize=16)
plt.ylabel("y", fontsize=16)
plt.xlim(self.xmin, self.xmax)
plt.tick_params(labelsize=16)
plt.scatter(self.x, self.y)
plt.show()
次にガウス過程の本体を書き上げます。chrはクロネッカーのデルタ$\delta(\cdot,\cdot)$です。
xmin = -7
xmax = 5
noise_level = 0.1
class GaussianProcess:
def __init__(self, theta1, theta2, theta3):
# thetax are used in rbf kernel elements
self.theta1 = theta1
self.theta2 = theta2
self.theta3 = theta3
self.xtrain = None
self.ytrain = None
self.xtest = None
self.ytest = None
self.kernel_inv = None # matrix
self.mean_arr = None
self.var_arr = None
def rbf(self, p, q):
return self.theta1 * math.exp(- (p-q)**2 / self.theta2)
def train(self, data):
self.xtrain = data.x
self.ytrain = data.y
N = len(self.ytrain)
kernel = np.empty((N, N))
for n1 in range(N):
for n2 in range(N):
kernel[n1, n2] = self.rbf(self.xtrain[n1], self.xtrain[n2]) + chr(n1, n2)*self.theta3
self.kernel_inv = np.linalg.inv(kernel)
def test(self, test_data):
self.xtest = test_data.x
N = len(self.xtrain)
M = len(self.xtest)
partial_kernel_train_test = np.empty((N, M))
for m in range(M):
for n in range(N):
partial_kernel_train_test[n, m] = self.rbf(self.xtrain[n], self.xtest[m])
partial_kernel_test_test = np.empty((M, M))
for m1 in range(M):
for m2 in range(M):
partial_kernel_test_test[m1, m2] = self.rbf(self.xtest[m1], self.xtest[m2]) + chr(m1, m2)*self.theta3
self.mean_arr = partial_kernel_train_test.T @ self.kernel_inv @ self.ytrain
self.var_arr = partial_kernel_test_test - partial_kernel_train_test.T @ self.kernel_inv @ partial_kernel_train_test
def chr(a, b):
if a == b:
return 1
else:
return 0
最後にmain関数と描画用の関数を書いて終わりです。
def draw(train_data, test_data, no_noise_data, mean_arr, var_arr):
xtest = test_data.x
xtrain = train_data.x
ytrain = train_data.y
var_arr = np.diag(var_arr)
boundary_upper = np.empty(len(xtest))
boundary_lower = np.empty(len(xtest))
for i in range(len(xtest)):
boundary_upper[i] = mean_arr[i] + var_arr[i]
boundary_lower[i] = mean_arr[i] - var_arr[i]
plt.figure(figsize=(15, 10))
plt.scatter(xtrain, ytrain, label="Train Data", color="red")
plt.plot(xtest, mean_arr, label="Predicted Line by limted test data")
plt.plot(no_noise_data.x, no_noise_data.y, label="GT without noise", color="black", linestyle='dashed')
plt.xlabel("x", fontsize=16)
plt.ylabel("y", fontsize=16)
plt.xlim(xmin, xmax)
plt.ylim(-0.5,3.5)
plt.tick_params(labelsize=16)
plt.title("Predicted line by Gaussian Process", fontsize="16")
plt.fill_between(xtest, boundary_upper, boundary_lower, facecolor='y',alpha=0.3)
plt.legend(["Predicted Line by limted test data", "GT without noise", "Train Data with noise", "confidence interval $\pm\sigma$"],fontsize=16)
plt.savefig("gp.png")
plt.show()
def main():
train_data = dataset.DataSet(xmin, xmax, num_data=50, noise_level=noise_level)
test_data = dataset.DataSet(xmin, xmax, num_data=1000, noise_level=noise_level)
no_noise_data = dataset.DataSet(xmin, xmax, num_data=1000, noise_level=0.0)
model = GaussianProcess(theta1=1, theta2=0.4, theta3=0.1)
model.train(train_data)
model.test(test_data)
draw(train_data, test_data, no_noise_data, model.mean_arr, model.var_arr)
if __name__ == '__main__':
main()
実験結果
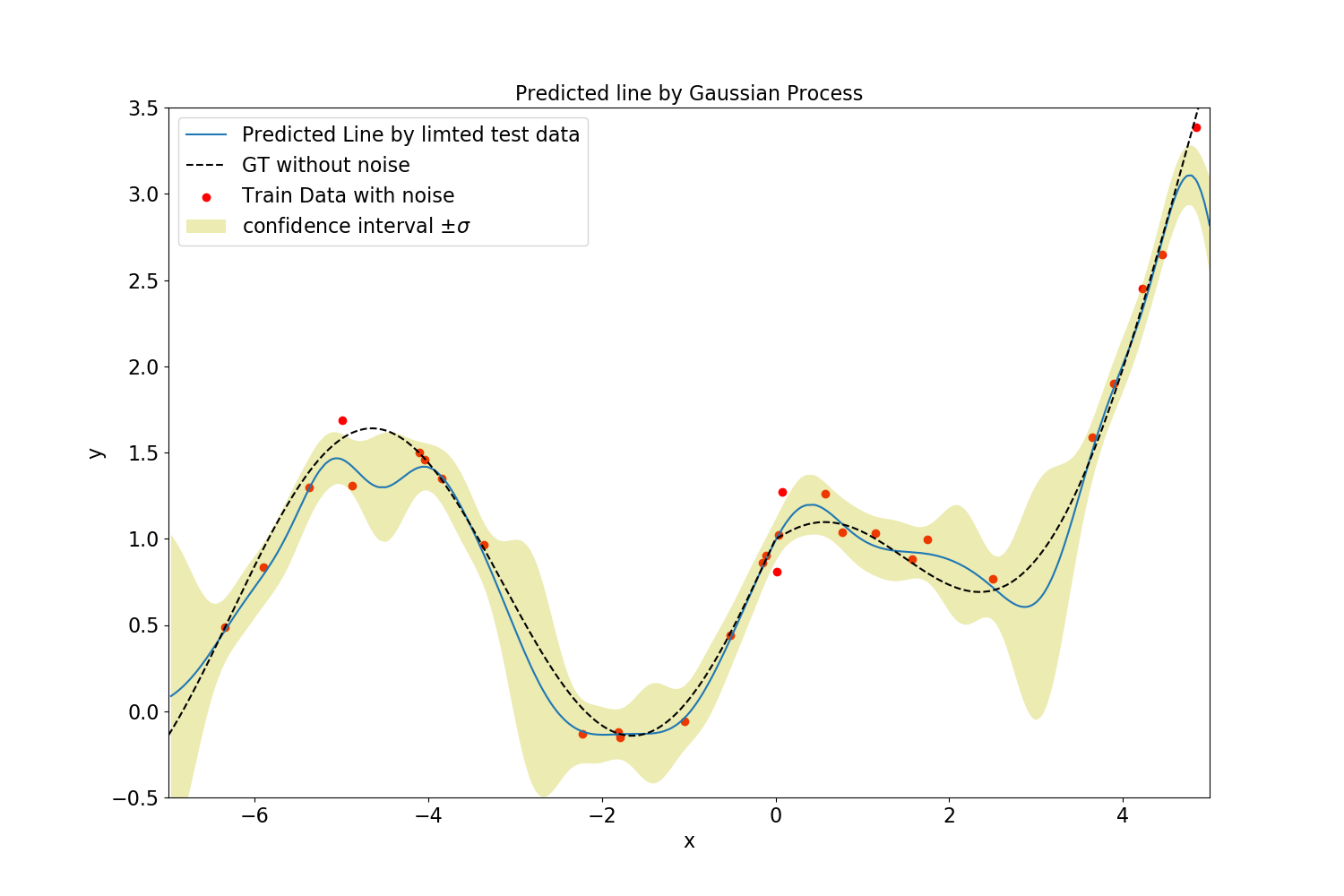
$M=30$の場合の結果を示します。訓練データ(赤丸)が足りていない領域では回帰の自信がない様子が分かります。noise_level=0.1にしました。$\theta_1=1, \theta_2=0.4, \theta_3=0.1$としました。
なお、ガウス過程回帰においては、データ数$N$の次元の行列の逆行列を計算するため、計算時間は$N^3$のオーダーになりますが、計算コストを大幅に減少させる様々な工夫(補助変数法など)が存在します。
徐々にデータ数を増やしていく様子を以下に示します。