本稿ではpythonのnumpyでガウス過程を実装します。パラメータの調整はマルコフ連鎖モンテカルロ法(MCMC)を使います。
ガウス過程について
実装に専念するので、基礎の説明は省略します。
ガウス過程は色んな記事に説明がありますが、一番お勧めはこちら
ガウス過程では、自変数たち$\bf x$に対する関数$\bf y(x)$は確率分布で表示されます。その分布は多変量正規分布
p(\mathbf{y}|\mathbf{x}) = \mathcal{N}(\mathbf{y}|\mathbf{\mu},\mathbf{\Sigma})
$\mu$は平均値で、$\mathbf{\Sigma}$は共分散行列。ただし、何の情報もない状態では普通に$\mu=0$とされます。$\mathbf{\Sigma}$はカーネル関数によって計算されます。
ここで情報のある自変数たちとそれに対する関数の値を$x_0$と$y_0$に、まだ情報なく新しい自変数たちとそれに対する関数の値を$x_1$と$y_1$にします。同時確率は
p(\mathbf{y}_0,\mathbf{y}_1|\mathbf{x}_0,\mathbf{x}_1) = \mathcal{N}(\mathbf{y}_0,\mathbf{y}_1|0,\textbf{K}_+)
ただし
\textbf{K}_+ =
\begin{bmatrix}
\textbf{K}_{00} & \textbf{K}_{01} \\
\textbf{K}_{10} & \textbf{K}_{11}
\end{bmatrix}
知りたい関数の確率分布$\mathbf{y}_1$は、何の情報もなく推測する場合、つまり事前分布は
p(\mathbf{y}_1|\mathbf{x}_1) = \mathcal{N}(\mathbf{y}_1|0,\textbf{K}_{11})
となりますが、$\mathbf{y}_0$と$\mathbf{x}_0$を知った後で推測する場合、つまり事後分布は
\begin{align}
& p(\mathbf{y}_1|\mathbf{x}_1,\mathbf{y}_0,\mathbf{x}_0) = \mathcal{N}(\mathbf{y}_1|\mathbf{\mu},\mathbf{\Sigma}) \\
\mathbf{\mu} &= \textbf{K}_{10}\textbf{K}_{00}^{-1}\mathbf{y}_0 \\
\mathbf{\Sigma} &= \textbf{K}_{11} - \textbf{K}_{10}\textbf{K}_{00}^{-1}\textbf{K}_{01}
\end{align}
となります。
詳しくは省略しますが、要するに何の情報もない時に平均値は0だと推測しかなく、共分散行列もその自変数たち$x_1$自体のカーネル関数で計算されますが、$y_0$と$x_0$の情報が入ったらそこからもっといい推測ができます。つまり、平均値$\mu$は知っている関数の値$y_0$とそれに対する共分散行列$K_{10}$と$K_{00}$から計算できます。共分散行列$\Sigma$も$K_{10}$と$K_{00}$の影響で値が小さくなって、予測がもっと明白になります。
ガウス過程の実装
例としてカーネルはRBF(放射基底関数)を使用します。
k(x,x') = a^2\exp^{-\left(\frac{x-x'}{s}\right)^2} + w^2\delta_{x,x'}
ここではホワイトノイズもカーネルに加えます。$a$と$s$と$w$はカーネルのパラメータ。後の例ではMCMCで調整するのですが、今はまず適当に設定して実装します。
ちなみにホワイトノイズをカーネルに含めずに別の形で計算する人もいますが、ここでは全部のパラメータをカーネルにある方が調整する時は便利だと思ってこうすることにしました
上述の方程式に基づいてnumpyで実装します。
import numpy as np
import matplotlib.pyplot as plt
class RBFkernel:
def __init__(self,*param):
self.param = list(param)
def __call__(self,x1,x2):
a,s,w = self.param
return a**2*np.exp(-((x1-x2)/s)**2) + w*(x1==x2)
def y(x): # 知りたい関数の正体
return 0.1*x**3-x**2+2*x+5
x0 = np.random.uniform(0,10,30) # 既知の点
y0 = y(x0) + np.random.normal(0,2,30) # 関数にノイズを加える
x1 = np.linspace(-1,11,101) # 探す点
kernel = RBFkernel(8,0.5,3.5) # 適当なパラメータを使うカーネル関数
k00 = kernel(*np.meshgrid(x0,x0))
k00_1 = np.linalg.inv(k00) # 逆行列
k01 = kernel(*np.meshgrid(x0,x1,indexing='ij'))
k10 = k01.T
k11 = kernel(*np.meshgrid(x1,x1))
# ここでは上述の方程式の通りのμとΣ
mu = k10.dot(k00_1.dot(y0))
sigma = k11 - k10.dot(k00_1.dot(k01))
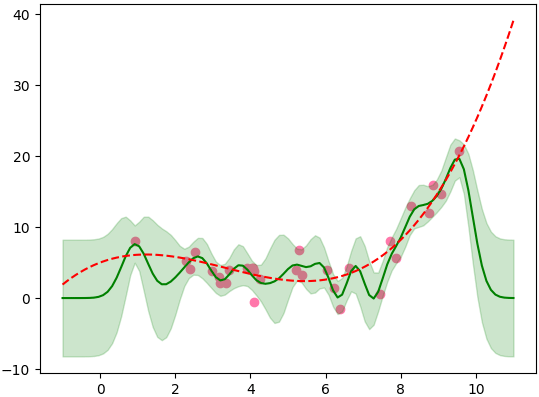
plt.scatter(x0,y0,c='#ff77aa')
plt.plot(x1,mu,'g') # 推測された平均
plt.plot(x1,y(x1),'--r') # 本物の関数
std = np.sqrt(sigma.diagonal()) # 各点の標準偏差は共分散行列の対角成分
plt.fill_between(x1,mu-std,mu+std,alpha=0.2,color='g') # 推測された標準偏差の中の領域
plt.show()
パラメータの調整はしていないため形がうねうねしてあまりいい答えとは見えませんね。
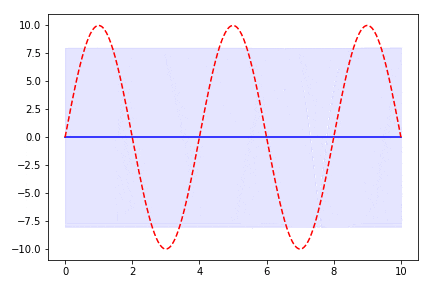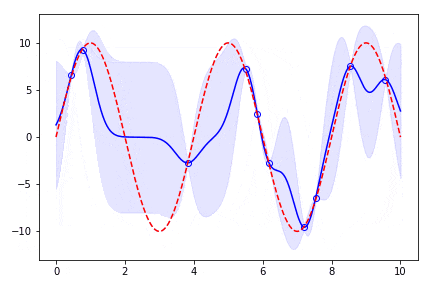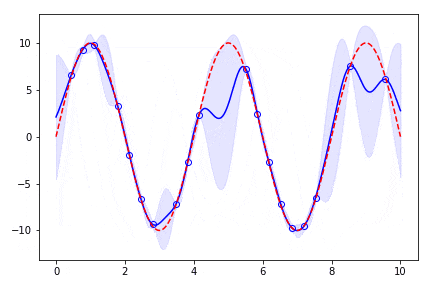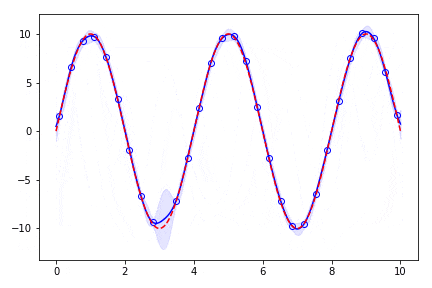
ガウス過程のアニメーション化
よくわかりやすくなるようにガウス過程を動画にしてみます。
import imageio
def y(x):
return 10*np.sin(np.pi*x/2)
n = 30
x0 = np.random.permutation(np.linspace(0.1,9.9,n))
y0 = y(x0) + np.random.normal(0,0.1,n)
gif = []
for i in range(n):
x1 = np.linspace(0,10,1000)
kernel = RBFkernel(8,0.5,0.1)
k00 = kernel(*np.meshgrid(x0[:i],x0[:i]))
k00_1 = np.linalg.inv(k00)
k01 = kernel(*np.meshgrid(x0[:i],x1,indexing='ij'))
k10 = k01.T
k11 = kernel(*np.meshgrid(x1,x1))
mu = k10.dot(k00_1.dot(y0[:i]))
sigma = k11 - k10.dot(k00_1.dot(k01))
std = np.sqrt(sigma.diagonal())
fig = plt.figure()
plt.scatter(x0[:i],y0[:i],color='w',edgecolor='b')
plt.plot(x1,mu,'b')
plt.plot(x1,y(x1),'r--')
plt.fill_between(x1,mu-std,mu+std,alpha=0.1,color='b')
plt.tight_layout()
fig.canvas.draw()
gif.append(np.array(fig.canvas.renderer._renderer))
plt.close()
imageio.mimsave('gp.gif',gif,fps=2.5)
既知の点が増えていくと答えの分布の範囲が狭くなっていくことがわかります。
マルコフ連鎖モンテカルロ法(MCMC)の実装
この前の記事でモジュールでMCMCを実装する方法を説明しましたが、今回はnumpyから実装します。MCMCの中でも色んなアルゴリズムがあるが、ここではメトロポリス法を使います。この記事
を参考として書いたのです。方法の詳しい説明もその記事で。
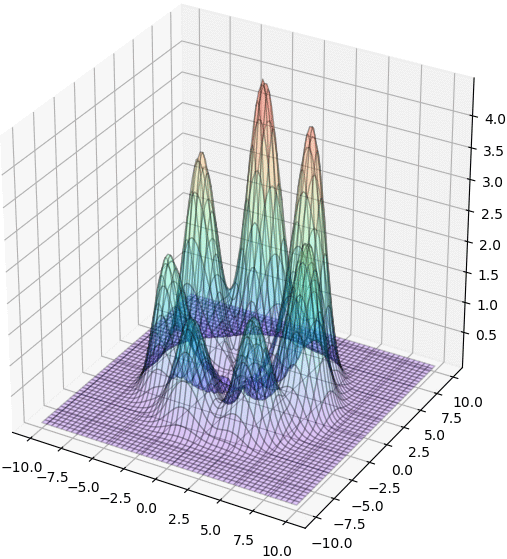
例として今回はこのような確率分布を使います。
from mpl_toolkits.mplot3d import Axes3D
def fn(xy):
x,y = xy
return np.exp(-(5**2-(x**2+y**2))**2/250 + xy[1]/10) * (7./4-np.sin(7*np.arctan2(x,y)))
plt.figure(figsize=[6,6])
mx,my = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
mz = fn([mx,my])
ax = plt.axes([0,0,1,1],projection='3d')
ax.plot_surface(mx,my,mz,rstride=2,cstride=2,alpha=0.2,edgecolor='k',cmap='rainbow')
plt.show()
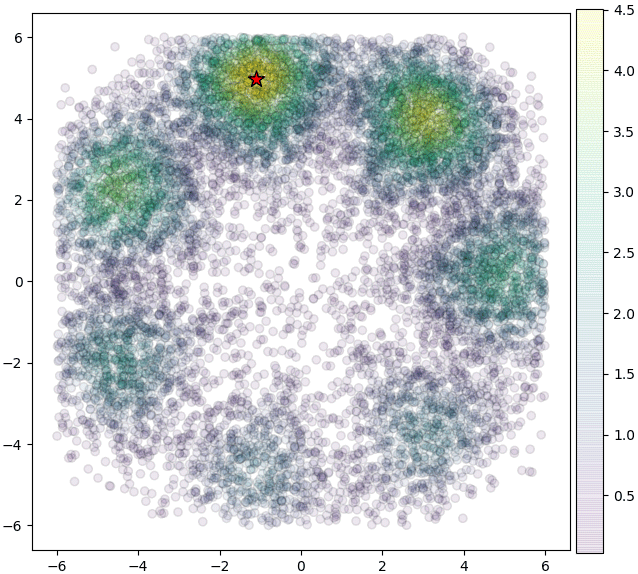
MCMCを使ってサンプリングします。
xy0 = np.array([3,-3]) # 開始の位置
bound = np.array([[-6,6],[-6,6]]) # 下限上限
s = (bound[:,1]-bound[:,0])/10. # 毎回どれくらい遠く移動するか
n = 16000 # 何度繰り返すか
xy = [] # 毎回の位置を格納するリスト
p = [] # 毎回の確率を格納するリスト
p0 = fn(xy0) # 開始の位置の確率
for i in range(n):
idou = np.random.normal(0,s,2) # 移動する距離
hazure = (xy0+idou<bound[:,0])|(xy0+idou>bound[:,1]) # 下限上限から外れたか
while(np.any(hazure)):
idou[hazure] = np.random.normal(0,s,2)[hazure] # 外れたものだけもう一度ランダムする
hazure = (xy0+idou<bound[:,0])|(xy0+idou>bound[:,1])
xy1 = xy0 + idou # 新しい位置の候補
p1 = fn(xy1) # 新しい位置の確率
r = p1/p0 # 新しい位置と現在の位置の確率の比率
# 比率は1より高い場合は常に移動するが、低い場合は確率で移動する
if(r>1 or r>np.random.random()):
xy0 = xy1 # 現在の位置を新しい位置に移動する
p0 = p1
xy.append(xy0) # 新しい位置を格納
p.append(p0) # 新しい確率を格納
xy = np.stack(xy)
x,y = xy[:,0],xy[:,1]
plt.figure(figsize=[7,6])
plt.gca(aspect=1)
plt.scatter(x,y,c=p,alpha=0.1,edgecolor='k')
plt.colorbar(pad=0.01)
plt.scatter(*xy[np.argmax(p)],s=150,c='r',marker='*',edgecolor='k') # 最大値を星で示す
plt.tight_layout()
plt.show()
ガウス過程のパラメータの調整
ガウス過程はカーネルとその中のパラメータによって答えは大きく違うので、パラメータを正しく選ぶのは必要となります。答えの良さは尤度関数で決まることが多い。ただし普通は対数の形で計算されます。対数尤度関数は
\ln f(\theta) = -\frac{1}{2}\ln|\mathbf{K}_{00}(\theta)| - \frac{1}{2}\mathbf{y}_0^T\mathbf{K}_{00}^{-1}(\theta)\mathbf{y}_0 - \frac{N}{2}\ln(2\pi)
$\theta$はカーネルのパラメータであり、調整したら尤度が変わります。ただし最後の項は$\theta$に関係ないので、省略できます。ついでに1/2も要りません。そうすると対数尤度関数はこうなります
\ln f(\theta) = -(\ln|\mathbf{K}_{00}(\theta)| + \mathbf{y}_0^T\mathbf{K}_{00}^{-1}(\theta)\mathbf{y}_0)
ガウス過程のパラメータの調整にMCMCを使う場合尤度関数はMCMCの確率分布となります。普段は調整する時そのままのパラメータを使うよりも、パラメータの対数が使われます。理由は大体のパラメータは程度のわからない正数だから、$-1,0,1,2,...$よりも、$0.01,0.1,1,10,...$という形で探す方が効果的です。なのでここで$\theta$はパラメータの対数を示します。
カーネルとガウス過程のクラスを定義します。
class Kernel:
def __init__(self,param,bound=None):
self.param = np.array(param)
if(bound==None):
bound = np.zeros([len(param),2])
bound[:,1] = np.inf
self.bound = np.array(bound)
def __call__(self,x1,x2):
a,s,w = self.param
return a**2*np.exp(-0.5*((x1-x2)/s)**2) + w**2*(x1==x2)
class Gausskatei:
def __init__(self,kernel):
self.kernel = kernel
def gakushuu(self,x0,y0): # パラメータを調整せず学習
self.x0 = x0
self.y0 = y0
self.k00 = self.kernel(*np.meshgrid(x0,x0))
self.k00_1 = np.linalg.inv(self.k00)
def yosoku(self,x): # xからyを予測
k00_1 = self.k00_1
k01 = self.kernel(*np.meshgrid(self.x0,x,indexing='ij'))
k10 = k01.T
k11 = self.kernel(*np.meshgrid(x,x))
mu = k10.dot(k00_1.dot(self.y0))
sigma = k11 - k10.dot(k00_1.dot(k01))
std = np.sqrt(sigma.diagonal())
return mu,std
def logyuudo(self,param=None): # 対数尤度
if(param is None):
k00 = self.k00
k00_1 = self.k00_1
else:
self.kernel.param = param
k00 = self.kernel(*np.meshgrid(self.x0,self.x0))
k00_1 = np.linalg.inv(k00)
return -(np.linalg.slogdet(k00)[1]+self.y0.dot(k00_1.dot(self.y0)))
def saitekika(self,x0,y0,kurikaeshi=1000): # パラメータを調整して学習
self.x0 = x0
self.y0 = y0
param = self.kernel.param
logbound = np.log(self.kernel.bound)
s = (logbound[:,1]-logbound[:,0])/10.
n_param = len(param)
theta0 = np.log(param)
p0 = self.logyuudo(param)
lis_theta = []
lis_p = []
for i in range(kurikaeshi):
idou = np.random.normal(0,s,n_param)
hazure = (theta0+idou<logbound[:,0])|(theta0+idou>logbound[:,1])
while(np.any(hazure)):
idou[hazure] = np.random.normal(0,s,n_param)[hazure]
hazure = (theta0+idou<logbound[:,0])|(theta0+idou>logbound[:,1])
theta1 = theta0 + idou
param = np.exp(theta1)
p1 = self.logyuudo(param)
r = np.exp(p1-p0)
if(r>=1 or r>np.random.random()):
theta0 = theta1
p0 = p1
lis_theta.append(theta0)
lis_p.append(p0)
self.ar_theta = np.array(lis_theta)
self.ar_p = np.array(lis_p)
self.kernel.param = np.exp(lis_theta[np.argmax(lis_p)])
self.k00 = self.kernel(*np.meshgrid(x0,x0))
self.k00_1 = np.linalg.inv(self.k00)
ここで.gakushuu()を使うとパラメータを調整せずにただ$x_0$と$y_0$を格納するが、.saitekika()を使うとパラメータの調整が行われます。
$\ln|\mathbf{K}_{00}(\theta)|$の部分は行列式の対数ですが、普通に行列式を計算してから対数を計算することにすると、行列式の値が小さすぎたり大きすぎたりするとアンダフローやオーバーフローになるので、安全のためにnp.linalg.slogdetを使うといいです。
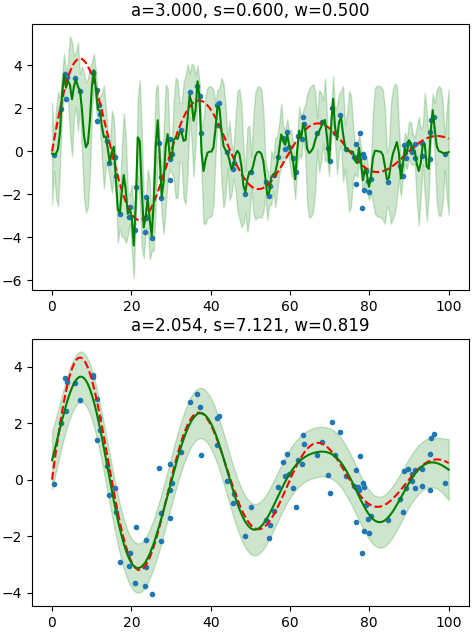
これを使ってパラメータ調整の前と後の結果を比べてみます。
def y(x): # 実際の関数
return 5*np.sin(np.pi/15*x)*np.exp(-x/50)
n = 100 # 既知の点の数
x0 = np.random.uniform(0,100,n) # 既知の点
y0 = y(x0) + np.random.normal(0,1,n)
param0 = [3,0.6,0.5] # パラメータの初期値
bound = [[1e-2,1e2],[1e-2,1e2],[1e-2,1e2]] # 下限上限
kernel = Kernel(param0,bound)
x1 = np.linspace(0,100,200)
gp = Gausskatei(kernel)
gp.gakushuu(x0,y0) # パラメータを調整せずに学習
plt.figure(figsize=[5,8])
for i in [0,1]:
if(i):
gp.saitekika(x0,y0,10000) # パラメータを調整する
plt.subplot(211+i)
plt.plot(x0,y0,'. ')
mu,std = gp.yosoku(x1)
plt.plot(x1,y(x1),'--r')
plt.plot(x1,mu,'g')
plt.fill_between(x1,mu-std,mu+std,alpha=0.2,color='g')
plt.title('a=%.3f, s=%.3f, w=%.3f'%tuple(gp.kernel.param))
plt.tight_layout()
plt.show()
パラメータを調整した後の結果の方がいいってのは一目瞭然。
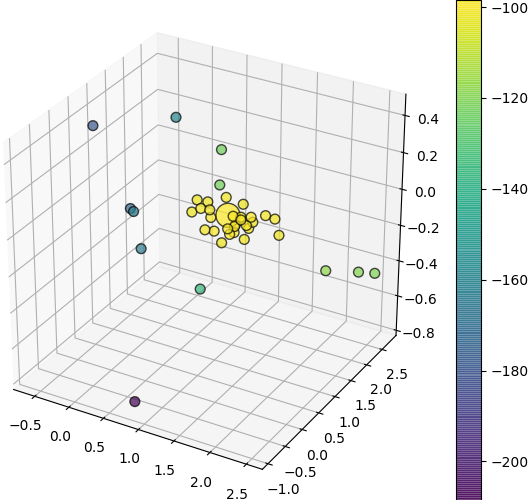
サンプリングされた全部のパラメータの値も格納されているので、3つのパラメータを3Dで表示してみます。点の色は対数尤度の値を示します。尤度の一番高い値は大きい点にします。
fig = plt.figure(figsize=[6,5])
ax = fig.add_axes([0,0,1,1],projection='3d')
sz = np.ones(len(gp.ar_p))*50
sz[gp.ar_p.argmax()] = 300 # 尤度の一番高いパラメータを大きく表示する
sc = ax.scatter(*gp.ar_theta.T,c=gp.ar_p,s=sz,alpha=0.7,edgecolor='k')
fig.colorbar(sc,pad=0)
plt.show()
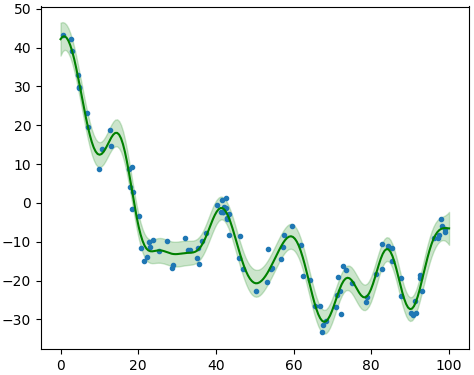
カーネルから生成されたノイズのパラメータの再現
カーネル関数で計算された共分散行列を使ってノイズのデータを生成することができます。ガウス過程を使ったら生成に使ったカーネル関数のパラメータを求めることができます。
ここではnp.random.multivariate_normalでノイズばかりのデータを生成してそのノイズを生成したカーネル関数のパラメータをガウス過程で求めてみます。
n = 100
x0 = np.random.uniform(0,100,n)
param = [20,5,3] # 実際のパラメータ
sigma = Kernel(param)(*np.meshgrid(x0,x0))
param0 = [4,0.4,10] # パラメータの初期値
bound = [[1e-2,1e2],[1e-2,1e2],[1e-2,1e2]]
y0 = np.random.multivariate_normal(np.zeros(n),sigma)
kernel = Kernel(param0,bound)
x1 = np.linspace(0,100,200)
gp = Gausskatei(kernel)
plt.figure(figsize=[5,4])
gp.saitekika(x0,y0,10000)
plt.plot(x0,y0,'. ')
mu,std = gp.yosoku(x1)
plt.plot(x1,mu,'g')
plt.fill_between(x1,mu-std,mu+std,alpha=0.2,color='g')
plt.tight_layout()
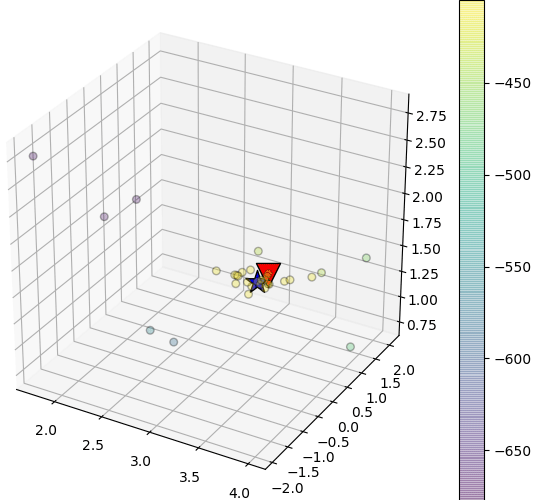
fig = plt.figure(figsize=[6,5])
ax = fig.add_axes([0,0,1,1],projection='3d')
sc = ax.scatter(*gp.ar_theta.T,c=gp.ar_p,s=30,alpha=0.3,edgecolor='k')
fig.colorbar(sc,pad=0)
ax.scatter(*np.log(param),c='r',edgecolor='k',marker='v',s=300) # 実際のパラメータを三角で示す
ax.scatter(*np.log(gp.kernel.param),c='b',edgecolor='k',marker='*',s=300) # 尤度の一番高いパラメータを星で示す
plt.show()
print('最適化の後のパラメータ: %s\n実際のパラメータ: %s'%(gp.kernel.param,param))
結果
最適化の後のパラメータ: [ 18.10334439 4.74039338 2.77129846]
実際のパラメータ: [20, 5, 3]
得られたパラメータの値は実際のと随分近いですね。ただしうまくいかない場合もあります。特にパラメータの数が多くなると再現は難しくなります。
sklearnとemceeで実装
おまけにモジュールを使って実装する方法も紹介してみます。ガウス過程はsklearnで簡単に実装できますが、パラメータの調整にMCMCを使う場合は他のモジュールを加える必要があります。ここではemceeというモジュールでMCMCを行います。
sklearnでのガウス過程の使い方はこちらの記事で詳しく説明してあります
emceeについてはこの記事で
実装の例
from sklearn.gaussian_process.kernels import RBF,WhiteKernel
from sklearn.gaussian_process import GaussianProcessRegressor as GPR
import emcee
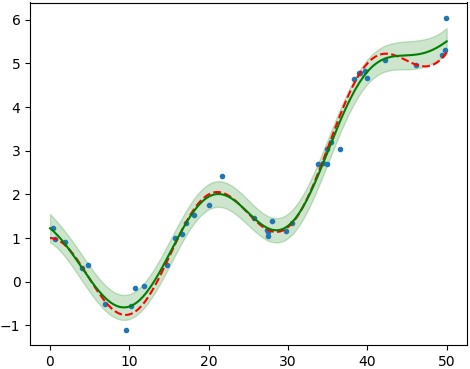
def y(x):
return np.cos(np.pi/10*x) + x**2/400 # 実際の関数
n = 40
x0 = np.random.uniform(0,50,n)
y0 = y(x0) + np.random.normal(0,0.25,n)
x1 = np.linspace(0,50,201)
kernel = 1*RBF()+WhiteKernel() # sklearnのカーネル
gp = GPR(kernel,alpha=0,optimizer=None) # MCMCで最適化するので、ここではoptimizer=None
gp.fit(x0[:,None],y0)
bound = np.array([[0.001,1000],[0.001,1000],[0.001,1000]]) # 下限上限
logbound = np.log(bound)
def lllh(theta): # emceeに使う分布関数
if(np.any(theta<logbound[:,0])|np.any(theta>logbound[:,1])):
return -np.inf
return gp.log_marginal_likelihood(theta)
nwalker = 20
ndim = len(gp.kernel.theta)
nstep = 50
theta0 = np.random.uniform(-2,2,[nwalker,ndim]) # パラメータの初期値
sampler = emcee.EnsembleSampler(nwalker,ndim,lllh)
sampler.run_mcmc(theta0,nstep)
theta = sampler.flatchain[sampler.flatlnprobability.argmax()] # 尤度を一番高くするパラメータ
gp.kernel.theta = theta # 新しく得られたパラメータを設定する
gp.fit(x0[:,None],y0) # 新しいパラメータでもう一度学習させる
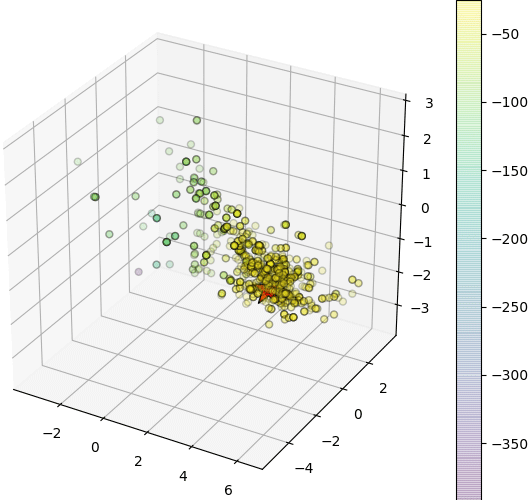
# サンプリングされたパラメータの値の分布
fig = plt.figure(figsize=[6,4.5])
ax = fig.add_axes([0,0,1,1],projection='3d')
sc = ax.scatter(*sampler.flatchain.T,alpha=0.2,s=100,c=sampler.flatlnprobability,marker='.',edgecolor='k')
plt.colorbar(sc,pad=0)
ax.scatter(*theta,s=600,c='r',edgecolor='k',marker='*') # 最大値の位置を描く
# 近似の結果
plt.figure(figsize=[5,4])
plt.plot(x0,y0,'. ')
mu,std = gp.predict(x1[:,None],return_std=True)
plt.plot(x1,y(x1),'--r')
plt.plot(x1,mu,'g')
plt.fill_between(x1,mu-std,mu+std,alpha=0.2,color='g')
plt.tight_layout()
plt.show()
ここで.log_marginal_likelihood()というメソッドで特定のthetaに対する対数尤度を計算してemceeに渡してMCMCを行います。今回使うカーネルも前と同じくRBFとホワイトノイズで、調整するパラメータも同じく3つありますが、厳密に言うとパラメータの意味はちょっと違います。3つのパラメータは$a^2$,$\sqrt{0.5}s$,$w^2$に当たります。
終わりに
以上ガウス過程でMCMCを使う方法を紹介しました。
他の実装の例としてこの記事も参考できます。
ただしパラメータの調整の方法も違って、ホワイトノイズもカーネルに含まずに$\beta^{-1}$という形で現れます。