homotopy.io の紹介

こんにちは。こちらは 証明支援系 Advent Calendar 2025 20日目の記事です。

homotopy.io と呼ばれるツールの紹介をします。一応 nlab のページ に "a web-based proof assistant" と書いてあるので、証明支援系だと思います。

いわゆる普通の証明支援系 (Lean, Agda, etc...) が (数理論理学的) 命題を扱うのとは大きく違って、homotopy.io が扱うのは "finitely presented globular $n$-categories" です (nlab より)。らしいです。

なおこの文章は「紹介」であり、チュートリアルではないので、操作方法などは書いていません。ごめんなさい。

扱えるもの

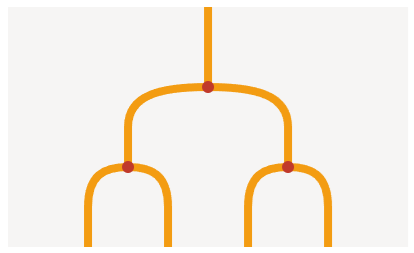
具体例を見るほうがわかりやすいと思うので、まずは見た目を紹介します。

こういうもの↑ を扱います。図はくっつく限り (境界が一致する限り) 横にも縦にもつなげて良くて、例えば上の図を組み合わせると下のような図が作れます。接続だけが重要で、大きさ (幅) に意味はありません。

この図たちには何の「意味」も与えられていません。が、これを例えば「橙線は集合 $A$ の元のこと」「赤丸は (下から上に読んで) $\times\colon A^2\to A$ のこと」とすれば「この合成したものは $(x,y,z,w) \mapsto (x\times y)\times (z\times w)\colon A^4 \to A$ のこと」だと解釈することができます。つまり、「図を書くことで $\times$ の合成関数を表現する」ことができます。

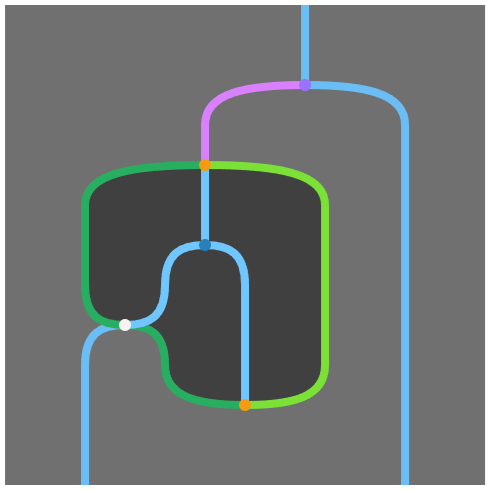
赤丸 (と橙の線 (と白領域¹)) だけでは大したことはできませんが、要素 (cell と呼びます) を自分で追加していくことで色々なものを図として表現することができるようになります。例えばこのような図を描けます:

今のところ 2 次元の図だけを表示していますが、homotopy.io では 3 次元の図も扱えます。

どころか、n 次元の図を扱うことができます。表示できるとは限りませんが。

ぺたぺたできる図を考えて何がしたいのか、というと:

• 証明したい事柄のある体系を図にエンコードして
• 証明したい事柄を図にエンコードして
• 証明を図にエンコードする

ことで、図を書くことで証明が完了する、ということがやりたいのです。

エンコードできるものはとても限られています。が、証明を図で描ける (= 証明の妥当性が明らかな状態で提示できる) というだけでも面白いのではないかと思っています。

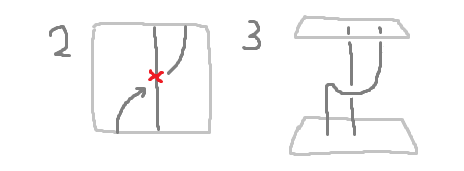
単純な例では「結び目の同値性の証明」を図として描くことができます。モノイドや群などの小さめの代数系なら、成り立つ性質を図に書き下すことである程度の等式を表現することができます。特に strict monoidal category なら strict 2-category だと思うことができる²ので、図³にエンコードできます。

今更ですが、ここで描いている図は string diagram / surface diagram と同じものです。圏の言葉ばかりになってしまいましたが、まぁそれはつまりとても汎用的であるというくらいの話です。

体系をエンコードしてみる

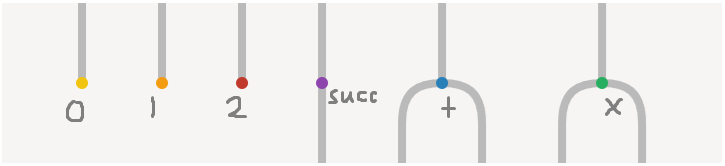
例えば $\mathbb{N}, 0, \mathsf{succ}, +, \times$ がある言語を考えてみます。$(1 + 1) \times 2 = 4$ くらいができると嬉しいです。次の文章は読み飛ばしても良いです。

ここから次のような strict monoidal category を考えることができます:

• 対象は $\mathbb{N}^n$ ($n$ 個の $\mathbb{N}$ の列), $\otimes$ は列の結合 (単位元は $\mathbf{1} = \mathbb{N}^0$)
• 射 $f\colon \mathbb{N}^m \to \mathbb{N}^n$ は $\mathbb{N}^m$ から $\mathbb{N}^n$ への写像
  • 例えば $0, 1, 2\colon \mathbf{1} \to \mathbb{N}$ がある (定数)
  • 例えば $\mathsf{succ}\colon \mathbb{N} \to \mathbb{N}$ がある (単項演算)
  • 例えば $+, \times\colon \mathbb{N}^2 \to \mathbb{N}$ がある (二項演算)

これを 2-category だと思って図に翻訳すると:

• 0-cell: $*$
• 1-cell: $\mathbb{N}\colon *\to*$
  • $\otimes$ は 1-cell の合成 $\circ$ になります
  • $\mathbf{1}$ は $\mathrm{id}_*\colon * \to *$ のことになります
• $0, 1, 2\colon \mathrm{id}_*\to\mathbb{N}$
• $\mathsf{succ}\colon \mathbb{N} \to \mathbb{N}$
• $+, \times\colon \mathbb{N}\circ\mathbb{N} \to \mathbb{N}$

となりそうです。

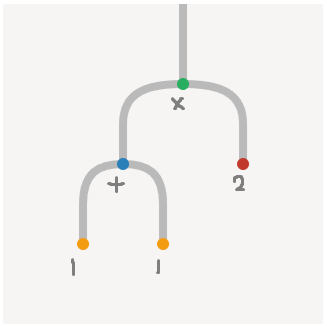
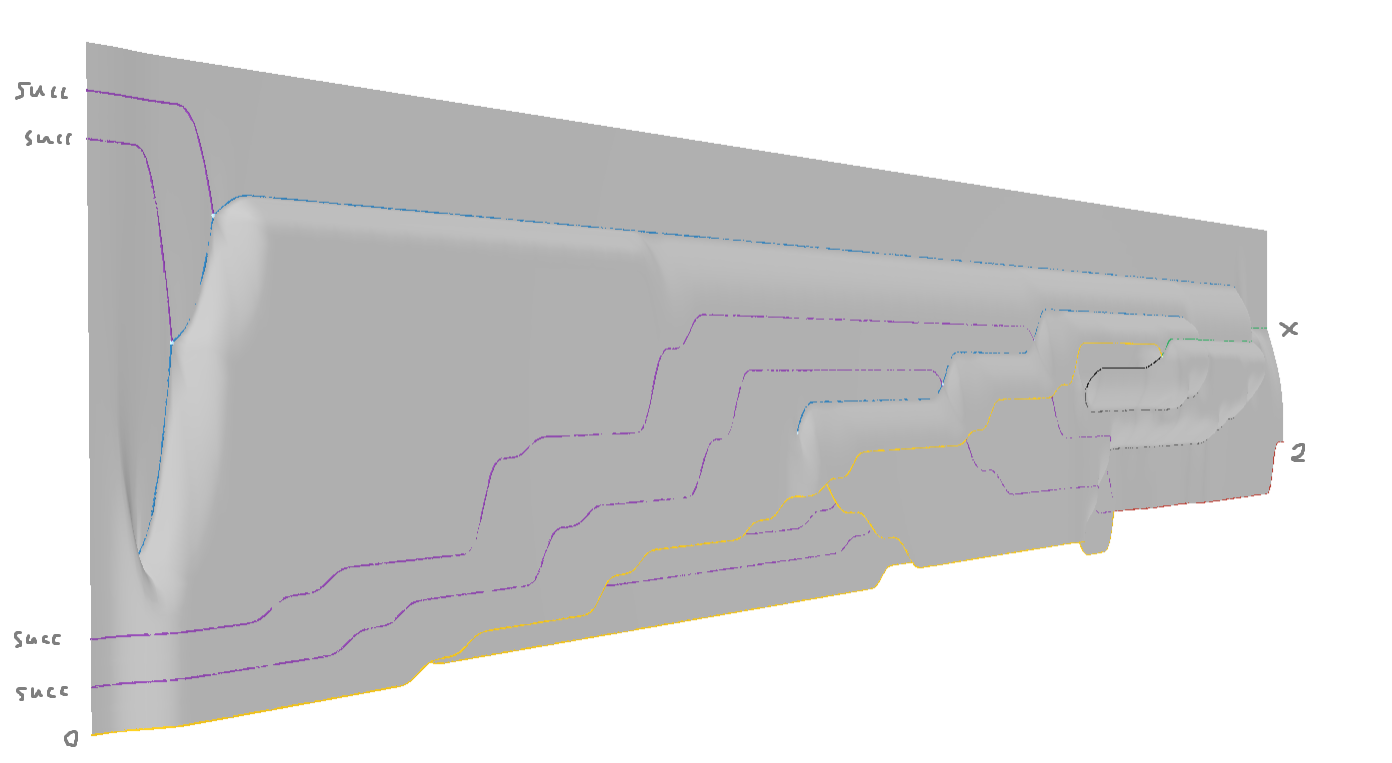
以上の圏の話は読み飛ばしていただいても大丈夫なのですが、結果的にこういう図↓ ができます (下から上に読みます)。内部で何が起きているのかわからなくても、この図は理解できると思います (なので細かいことは省略しました)。

とりあえず $(1 + 1) \times 2$ くらいは表現できます。

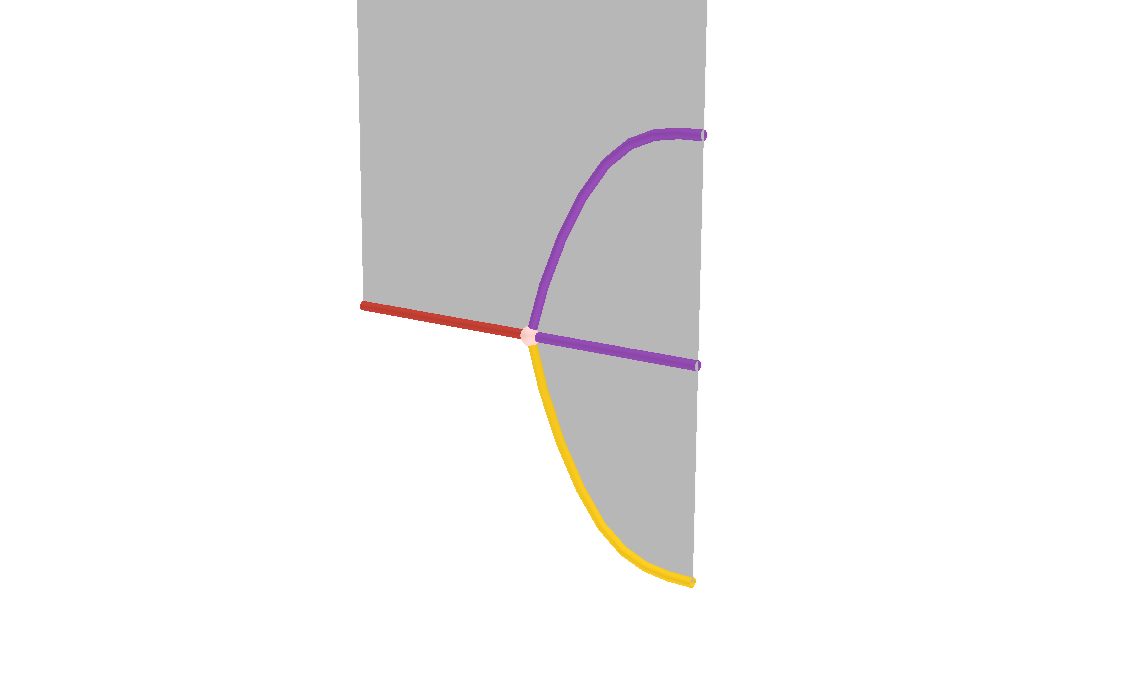
ところで、$1 = \mathsf{succ}(0), 2 = \mathsf{succ}(\mathsf{succ}(0))$ だと思います⁴。このような等式を、homotopy.io では「1次元上(<うえ)の図 (cell)」として表現します。つまり…ある ($n$ 次元の) 図から、別の ($n$ 次元の) 図への、変形を表す ($n+1$ 次元の) 図になります。…見たらわかると思います。

こういう等式があるはずで (2次元の図の間の等式)。それを:

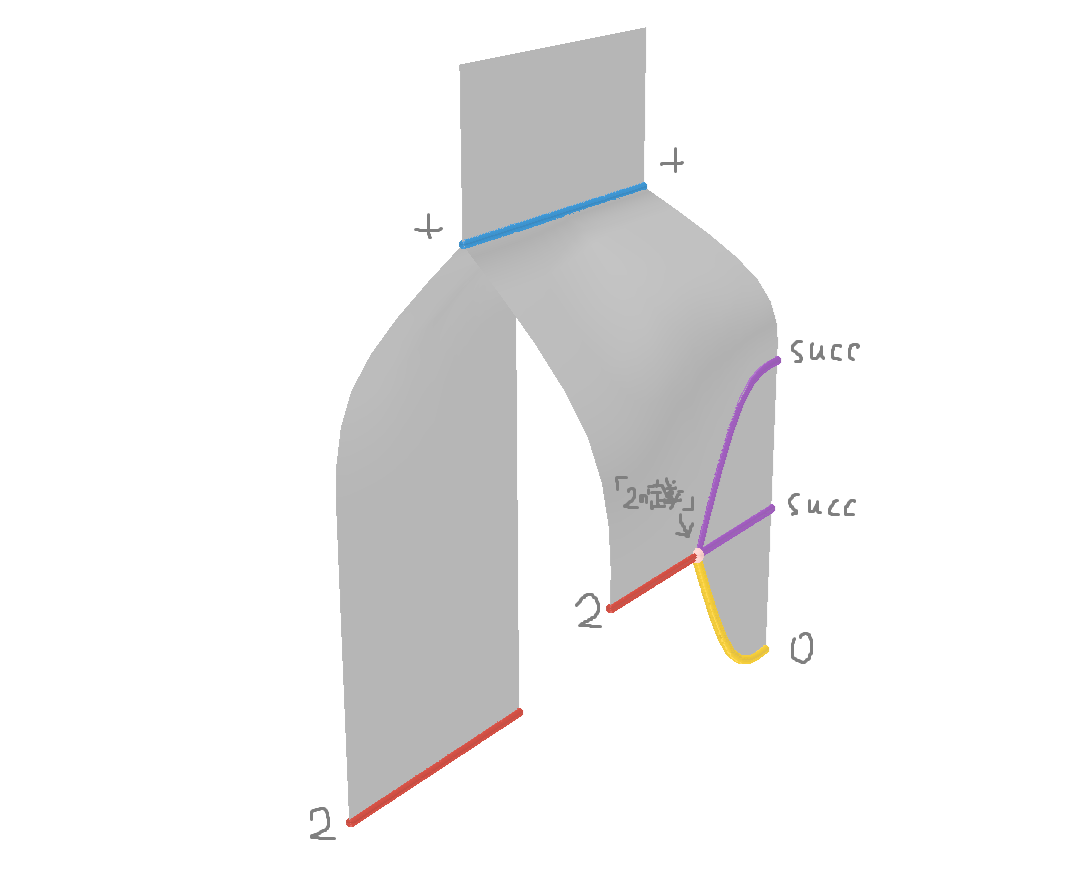
このように (3次元の図で⁵) 表現します。新たに生まれた真ん中の点 (3-cell) は、言わば「$1$ の定義」ということになります。同様に「$2$ の定義」も与えることができます。

紙面上で書くには3次元の図はとても面倒なので、「2次元の図の変化」として認識したほうがわかりやすい気がします。また、homotopy.io では下図のように 1 つ次元を潰した図として表現されることもあります (今回みたいな幅が狭い図なら情報はそんなに失われませんね) (軸の向きが homotopy.io の都合で変わっています)。

さて、$+, \times$ にも同様に定義を与えることができます。$\mathbb{N}$ の induction で定義するとしたら:

• $x + 0 = x$
• $x + \mathsf{succ}(y) = \mathsf{succ} (x + y)$
• $x \times 0 = 0$
• $x \times \mathsf{succ}(y) = x \times y + x$

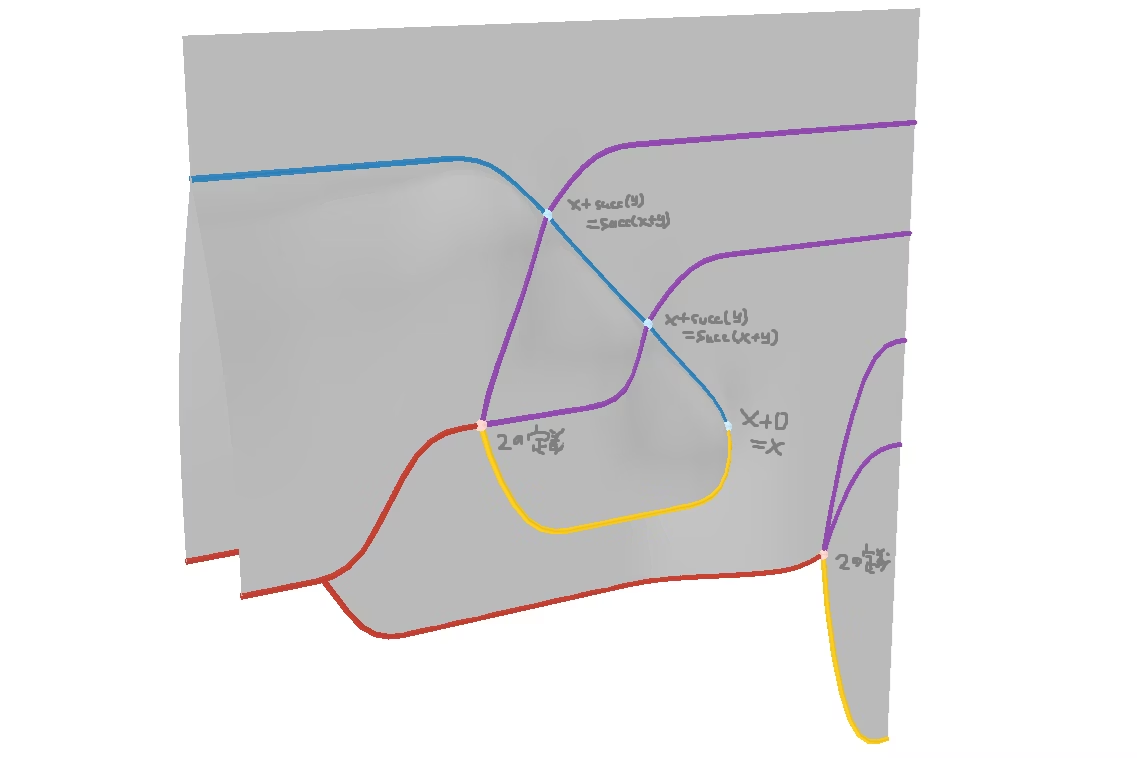
このような定義が一般的かと思います。$+$ の2つの等式をそのまま図として表現してみますと:

こうなります。入出力の型 (境界部分) がそれぞれ一致していることが確認できます。$x, y$ についての量化が「図の外側から値がやって来ること (= 何を外側に接続したとしても～)」で成されていて、ちょっと興味深いです。

なお、現時点では誰も「自然数が $0$ と $\mathsf{succ}$ だけで出来ている」とは言ってないことに注意が必要です。結論から言うとこのシステムでは inductive definition は作れないので、そういうこと (場合分けとか) がしたいときには、このシステムは何も役に立ちません。

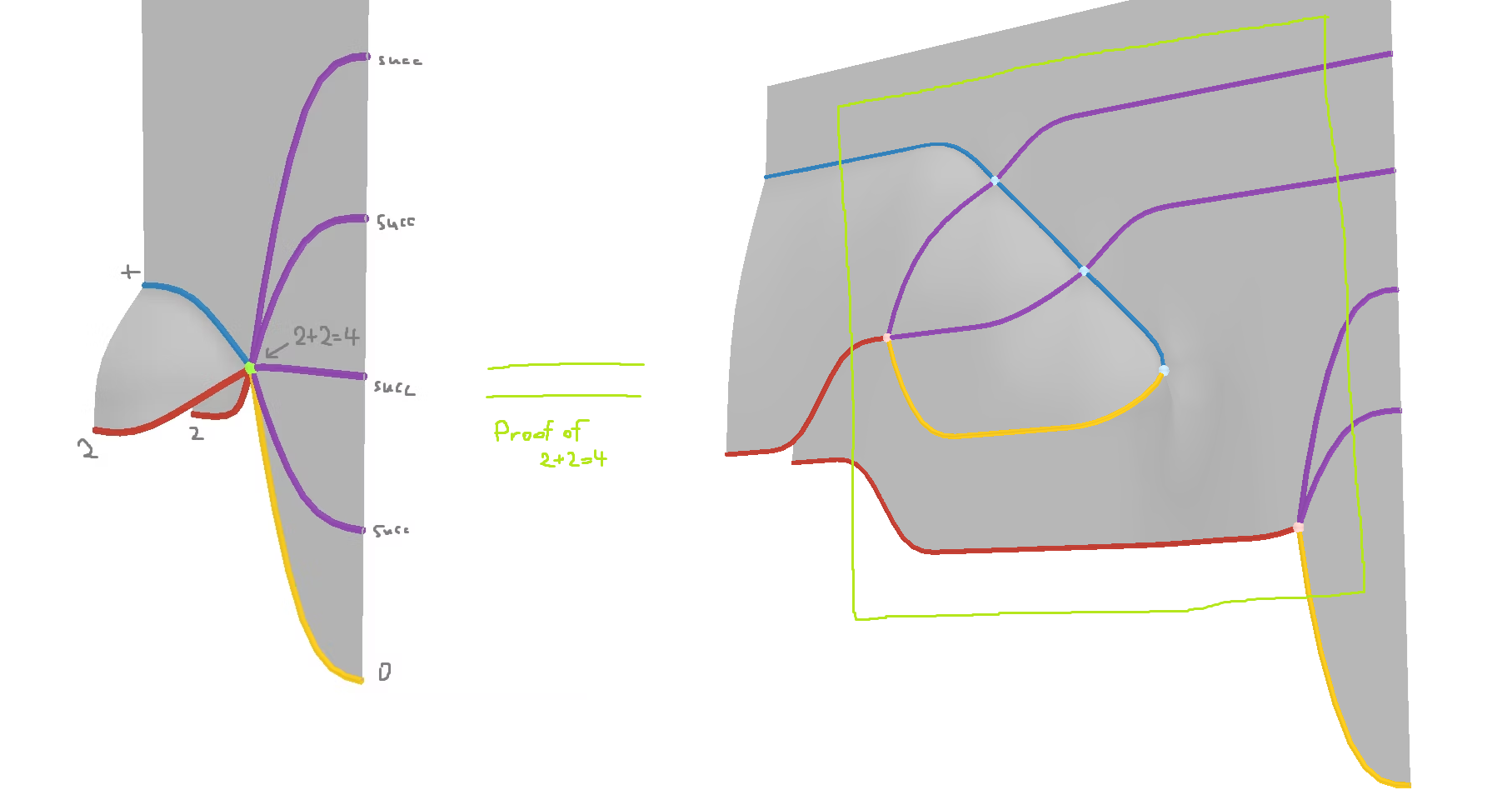
この段階で、先程までで定義した等式群 ($2$ の定義、$+$ の定義) を使って、$2 + 2$ を "手計算" することができます。$4$⁶ です。直観的にはこのようになります:

通常の証明で「等式変形を式の一部に適用する」(Agda で言う cong, ap) ような操作は、図の上では「変形図を一部にだけ貼り付ける」という操作として実現されます (つまりこの変形群は、妥当なのです)。逆に言うと、このような (cong, ap 相当の) 操作の正当性はこのシステムでは「見た目から明らかである」とされている、ということになります。

これは「『$2$ の定義』に対して $+$ と $2$ の identity を貼り付けた図」です。つまり $2 + 2 = 2 + \mathsf{succ}(\mathsf{succ}(0))$ という等式を意味しています。

先程の $2 + 2 = 4$ の等式変形を全部記すとこう↑ なります (見づらいですが、赤線と黄線は灰面の端 (boundary) です (魚のエラみたいになってます)。また、裏面には 3-cell はありません)。

さて、今回 $2 + 2 = 4$ という等式を得ましたが、これは正確には:

\begin{align}
2 + 2 &= 2 + \mathsf{succ}(\mathsf{succ}(0))\\
&= \mathsf{succ}(2 + \mathsf{succ}(0))\\
&= \mathsf{succ}(\mathsf{succ}(2 + 0))\\
&= \mathsf{succ}(\mathsf{succ}(2))\\
&= \mathsf{succ}(\mathsf{succ}(\mathsf{succ}(\mathsf{succ}(0))))\ (= 4)\end{align}

という長い等式です。今後この等式を「定理」としてどこかで応用するためには、この「長い等式」を証明として (witness として)、短い等式 $2 + 2 = 4$ を気軽に使えるような状況にしたいです。

そこで、「$2 + 2 = 4$ を表す図を一旦勝手に追加し」「その図と、先程の長い等式の図が等しいことを示す図も追加する」ことを行います。

つまりこのような状況を作ります:

左図の、黄緑の 3-cell を勝手に追加した上で、それが右図に等しいという 4-cell (等式のこと) を追加することで、「定理と呼ばれるもの」を作ることができます。実際、今後何かの証明で $2 + 2 = 4$ であることが必要になったらちっちゃい 3-cell の方を適用できて、且つその中身 (= 証明) を (4-cell を通して) 見ることができるというのなら、それは定理であろう、というところです。

ちなみに homotopy.io では 4 次元の図は「3 次元の図のアニメーション」として表示することができます。わかりやすいかはさておき、表示することはできます。

一旦のまとめ

$2 + 2 = 4$ の証明を通して:

• 証明したい事柄のある体系を図にエンコードして
• 証明したい事柄を図にエンコードして
• 証明を図にエンコードする

という構造を確認しました。以上からわかるように、homotopy.io で色々なものを表現できるのは確かですが、いわゆる定理証明支援系とは大きく異なっています:

• 計算はしてくれない。全部自分で equality を繋ぐ必要がある。
  • というか、normalization などの概念がない。
• 依存型や帰納的データ型などの、「証明に必須」とも言える概念たちが存在しない。
• 実質、等式 (正確には reflexive かつ transitive なもの⁷) しか書けない。

しかし、それでもいくつかの興味深い特徴を持っています:

• あまりにも何もないので、まっさらな体系を考えることができる。
  • 私たちがいつも機械に代行させている「計算」の恩恵を感じられる。
• 「一部に図を貼り付ける」という、cong, ap 相当の操作がある。
• 「定義」や「定理」相当のものを表現することができる。

ちなみに homotopy.io の (操作を含めた) チュートリアルは こちら にあります。興味を持った方は是非やってみるのをおすすめします。

余談: 私が homotopy.io (旧 Globular) を知った⁸のはこのあたりの記事だったと思います (全て m-hiyama さんのブログ):

• 絵算ベースの証明支援系 Globular
• Globularの威力をお見せしよう
• 「コミュニケーションの多次元化」という革命に立ち会っているのだと思う

正直 Globular も homotopy.io も使いづらいところがずっとある⁹のですが、「図式計算」自体はかなり面白いものだと思っていて、なにかこう、可能性を感じています。私はその辺りのことをよく考えています。余談終わり。

 

以後、こういうことをしたいときはどうなるかという話をいくつか置いておきます。

構造規則

$+$ と同様に、$\times$ についても定義を与えたいところですが、$x \times 0 = 0$ を作るには右辺側で「入力としてやってきた $x$ を捨てる」必要があります。このシステムには「値を捨てる」みたいなものはないので、作ります。

同じ話で、$x \times \mathsf{succ}(y) = x \times y + x$ を作るには「$x$ を増やす」そして「$y$ と $x$ を交換する」操作が必要です。いわゆる構造規則 (Weakening, Contraction, Exchange) たちですね。

ではこの3演算 (drop, dup, swap) を追加したから十分か、というとそんなことはありません。もちろんこれらの定義 (意味付け) が必要です。

演算の定義は「有り得る組み合わせ」の数だけ必要です。元々 $\mathbb{N}$ として出現しうるものは $0$ と $\mathsf{succ}$ だけだったので、各演算 $+, \times$ について 2 通りずつ用意すれば十分でした。

しかし、drop, dup, swap が追加されたことで、$\mathbb{N}^n$ は「$0, \mathsf{succ}$, drop, dup, swap で生成される代数を適切に割ったもの」として扱う必要が出てきてしまいました。更に言うと $+, \times$ にも構造規則を適用するためにはそれらも生成元として扱う必要があります。

結果的にはこのようになります (命名は適当です、特に convention とかはない気がします):

drop, dup が Comonoid を成していることがわかるあたりが可愛いですね (counit = drop dup L/R, coassoc = dup dup)。

お分かりになられる通り、とてもつらいです。

何はともあれ、これで $2 \times 2$ も計算できるようになりました。$4$ でした。

やっていることが証明らしい証明では一切ないのですが、実際 homotopy.io には induction が無いので $+$ の commutativity/associativity や、$+, \times$ の distributive law などは証明できません。何かの証明に必要になったときに新たな等式として導入することはできます。

induction を書きたい

システム自体に induction はないのですが、作れない、こともない、です。どちらかというと問題は関数の方です。$\mathbb{N}$ の fold は $a$ と $a \to a$ を受け取って $\mathbb{N} \to a$ を作るものですが、つまり $a \to a$ を表現する必要があります。

$a = \mathbb{N}$ に限定したとしても $\mathbb{N} \to \mathbb{N}$ に関する操作 (apply とか、λ 抽象相当とか) を入れなきゃいけないことに違いはありません。ある程度のやりようはあるんですが、何にせよつらいです。

• 「領域」を作って λ 抽象をそのまま書けるようにする
  
  • 柔軟に書けそうに見えるのですが、領域を dup しようとすると (間に swap 相当のものを色々挟む必要があって) 大変なことになってつらいです。
• コンビネータ的に関数を構成する
  
  • SKI さえ書ければ完全なわけですが、型 ($a \to (b \to c)$ とか) を用意するのが厳しいので、現実的な範囲では型無しでやるしかないと思います (上の図はそうなっています)。
  • 各関数 ($\mathsf{succ}, +$) に η 変換版をそれぞれ用意しなければいけなくて大変そうでした。それぞれに drop/dup も必要です…。

homotopy.io はそういう目的のものではないので大変になってしまうのは当然ではあるのですが。普段どれくらい恵まれてるか実感できるような気もします。

なお、この ind を用意したところで別に自由な induction¹⁰ が回せるわけでは無いので、symmetry などは相変わらず証明できません。$+, \times$ を inductive っぽく定義できるというだけです。

swap を使えるようにする

drop/dup は仕方ない¹¹として、「swap だけでもどうにかする」方法があります。

これまで (strict) monoidal category を 2-category だと見做すという話から図への翻訳を考えてきましたが、どうやら braided monoidal category を 3-category と見做せる、また symmetric monoidal category を 4-category と見做せる、という話があるようです。この辺？

つまり次元を上げると勝手に swap がついてくるということです。図で見るとそうかも、という気になれます¹²。

元の圏の対象 $x$ を、これまでは $\ast \to \ast$ である 1-cell に翻訳してきましたが、braiding が欲しい場合は $\mathrm{id}_* \to \mathrm{id}_*$ である 2-cell として、symmetry まで欲しい場合は $\mathrm{id}_{\mathrm{id}_\ast} \to \mathrm{id}_{\mathrm{id}_\ast}$ である 3-cell として翻訳してあげることで、それらの性質が勝手についてきます。

実際 homotopy.io で構成してみると braiding として表示されます。3D View だと前後関係がわかりやすい…です。おそらく。

高次元になることで、代わりに操作がしづらくなります。難しいです。

symmetry の証明 ($\sigma = \sigma^{-1}$) を作ろうとしてみたんですがよくわかりませんでした。symmetry は 4-cell で、その間の等式なので 5-cell を扱う必要があるのですが…。どうやったらやりたい操作ができるんでしょうね…¹³。

contraction について

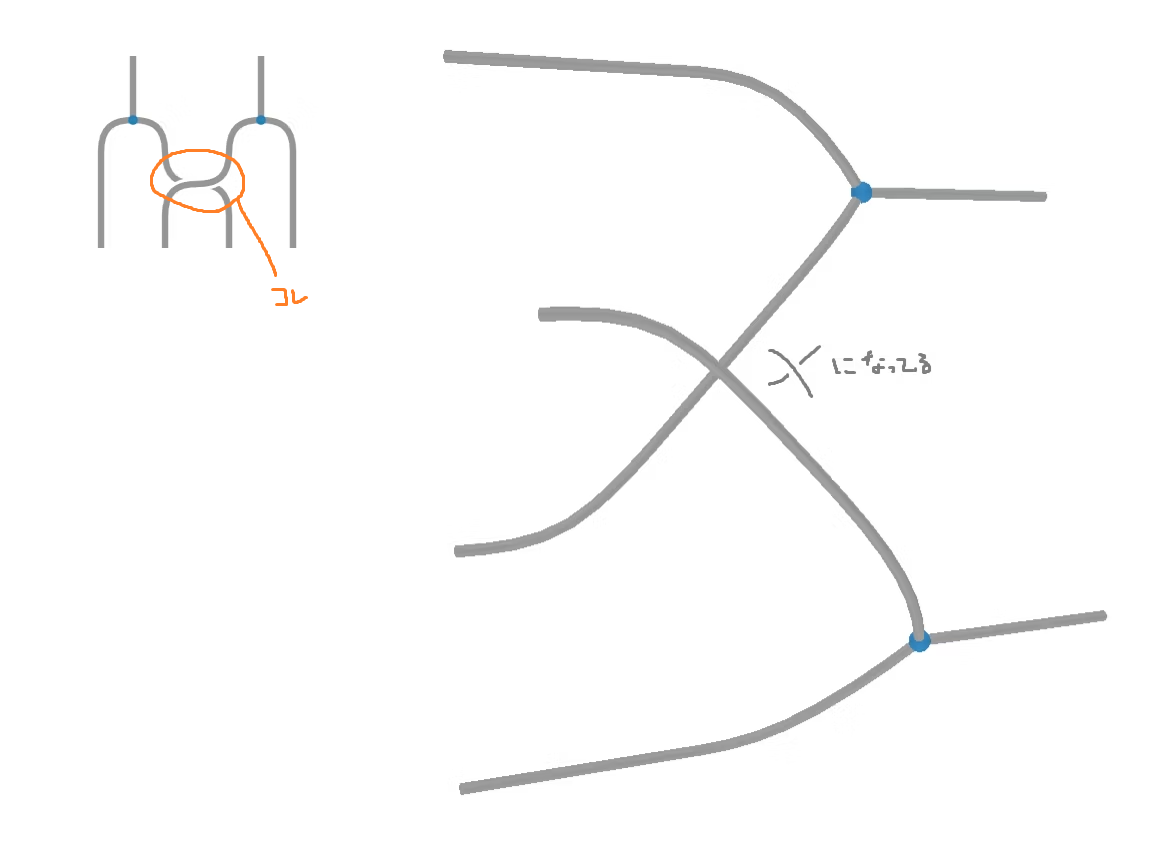
Globular から homotopy.io になって大きくアップデートされた部分が、"contraction" と呼ばれている機能なのだと思います。簡単に言えば「cell を横に並べる仕組み」です。

この 3 つは図式的には (= 見た目的には) 明らかに同じものであり、実際 2-category の interchange law に相当する等式になっています (homotopy.io で描けます)。Globular では「各行に丁度 1 つの cell がある」という要請があり、中間の形式が存在しませんでした (interchange law は左図と右図を直接繋いでいました)。

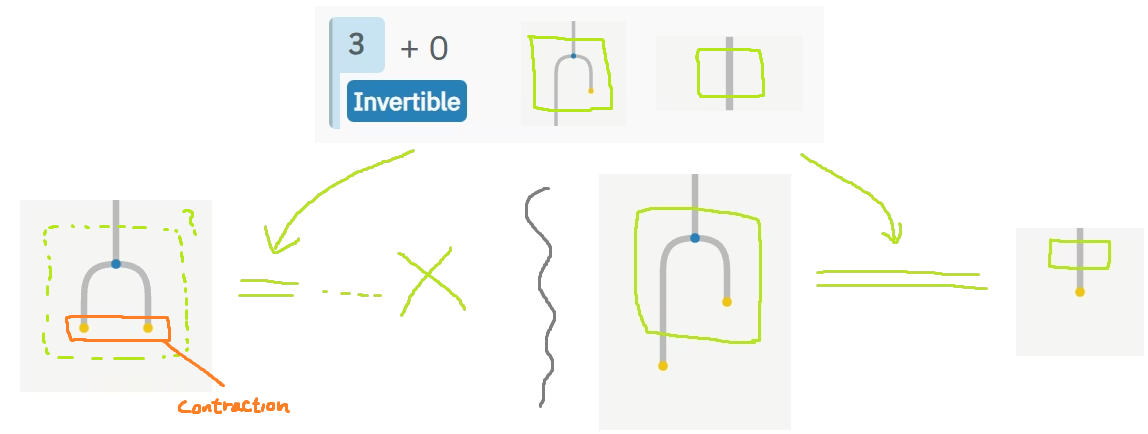
homotopy.io では、「複数の cell を (homotopy に沿って) contract したもの」(中央の図) が表現できるようにシステムが拡張されています。cell 群の contraction は unique に定まっていて¹⁴、これによって (contraction を通して)「homotopic な 2 つの図の間を行き来する」操作が実現されています。

この機能によって (homotopy.io 自身の) システムに手動で¹⁵各 coherence を導入しなくて良くなった、ということなのかなと思っているのですが、代わりにユーザー的には操作が面倒になりました。入れ替えたいだけなのに一旦 contraction を挟む必要があるので。

また、「等式の部分的な適用」をするためには当然 source (または target) が一致している必要があるのですが、一部が contraction になっていると、それは別の図として扱われているので、そのままでは使えない、ということがしばしば発生します。

見た目が綺麗になるようにと思って潰してしまうと後で 1 操作増えるみたいなことがあります。仕組みがわかっていれば概ね問題になることはないのですが…。

まとめ

具体的に何かやろうとすると難しいという話が後半になってしまいましたが、何であれ、面白いシステムではあると思っています (インタフェース次第でもっと柔軟になるのではと思っています)。

操作方法の話は一切できませんでした (すみません)。先に挙げたチュートリアル や 論文 に操作は書いてあるのですが、私はさほど把握しておりません (感覚で触っています)。

何かしらの興味を持っていただけていれば幸いです。

1. 下の図を見てわかるように、領域部分も扱う対象です。 ↩

2. 0-cell を $*$ のみ、各対象 $x$ を 1-cell $x\colon * \to *$ とし、1-cell の合成を $\otimes$ にして、射 $f\colon a \to b$ を $a$ から $b$ への 2-cell だと見なす。 ↩

3. 今回「図」と呼んでいるものは合成の associativity が strict に成り立つことを仮定しています (まぁ図なので、直観的にはそうあってほしい)。 ↩

4. 定義した $0, 1, 2, \mathsf{succ}$ が通常のものであるなら。 ↩

5. ペラいので 2 次元に感じるかもしれませんが、今回偶然そういう図しか登場しなかっただけです。 ↩

6. 正確には $\mathsf{succ}(\mathsf{succ}(\mathsf{succ}(\mathsf{succ}(0))))$ ↩

7. つまり、圏。 ↩

8. 某所に 2016 年末に書いた私の文章があってウケる。9 年経ってやってること変わってない… ↩

9. 別に何かに実用しようとかしているわけではないのですが。 ↩

10. $(C: \mathbb{N} \to \mathcal{U}) (z: C(0)) (s: (n: \mathbb{N}) \to C(n) \to C(\mathrm{succ}(n))) \to (n: \mathbb{N}) \to C(n)$ のこと ↩

11. linear な体系、扱いたいですよね。 ↩

12. braiding はこれだけ (3 の図) で十分です。symmetry の場合は加えて $\sigma = \sigma^{-1}$ が必要なのですが、次元を一個上げことでそのような homotopy を構成できるようになることがわかります。これはこの辺を考えていたときの写真。 ↩

13. 折角 n 次元図形を扱おうというのに操作がただのマウスの 2 次元入力ってそれどうなんってすごい思ってます。 ↩

14. colimit らしいです。論文に書いてありました。 ↩

15. 見るからにつらそう。 ↩