フラクタル図形で学ぶ「再帰処理」

高井です。

今回は「再帰処理」について解説します。
ついでにフラクタル図形を描いて遊んでみます。

プログラミングにはProcessingを使います。

再帰の解説は初心者向けの内容になりますので、分かる方はフラクタル図形とはまでスキップ！

再帰処理とは

ある関数が、処理の中で自分自身を呼び出すようなプログラムを「再帰処理」「再帰関数」などと呼びます。

簡単な例

整数1～nを足し算するプログラムを作ります。

数式で書いてみると

// 1～1の総和
sum(1) = 1;

// 1～2の総和
sum(2) = 1 + 2;

// 1～3の総和
sum(3) = 1 + 2 + 3;

...

となり、前の数字までの和 ＋ 今の数字であることがわかります。

// 1～1の総和
sum(1) = 1;

// 1～2の総和
sum(2) = sum(1) + 2;

// 1～3の総和
sum(3) = sum(2) + 3;

...

// nを使って表す
sum(n) = sum(n-1) + n;

これをプログラムにしてみるとこんな感じです↓

void setup(){
  int result = sum(10);
  
  println(result); // コンソールに結果出力
}

int sum(int n){
  return sum(n - 1) + n;
}

sum関数の中でsum関数を呼び出していますね！これが再帰だ～！

喜びも束の間、
これを実行するとStackOverflowErrorというエラーになります。

Java公式ドキュメントを見ますと

アプリケーションでの再帰の回数が多すぎてスタックオーバーフローが起こる場合にスローされます。

とのこと。
※ProcessingはJava言語が元になっています

何が起きているかというと

// n = 1 のとき
sum(1) = sum(0) + 1;

// n = 0 のとき
sum(0) = sum(-1) + 0;

// n = -1 のとき
sum(-1) = sum(-2) + (-1);

...

という風に無限に続いてしまうためエラーになってしまいます。
今回は1～nまでの足し算をしたいので、n=1で止めてあげる必要があります。

void setup(){
  
  int result = sum(10);
  
  println(result); // コンソールに結果出力 -> 55
}

int sum(int n){
  // 終了条件
  if(n == 0){
    return 0;
  }

  // 自分自身を呼び出す
  return sum(n - 1) + n;
}

これで完成です！

実際に再帰を使うときも、メモリ容量や処理時間を考慮して適切な終了条件を設定する必要があるでしょう・・・。

再帰処理はこのように
・関数が自分自身を呼び出している
・終了条件がある
ことが特徴です。

使いどころ

自分の経験として、再帰を使ったことがある事例です↓
・フォルダ内探索（指定されたファイルが見つかるまで探索する）
・オセロAI（n手先まで読んで最善手を探す）

他にもいろいろ応用されているみたいです。今後出会うかもしれませんね～
https://qiita.com/drken/items/23a4f604fa3f505dd5ad

フラクタル図形とは

図形の一部を拡大すると、また同じような図形が現れるもののことをフラクタル図形と言います。

下の絵は、大きな正三角形の中に小さな正三角形があり、その中にさらに小さな正三角形が…と続いています。
この絵は「シェルピンスキーのギャスケット」といって有名らしいです。

Wikipediaには

図形の部分と全体が自己相似（再帰）になっているものなどをいう

とあります！キタ！再帰！

描いてみた

作戦

作戦はこうです。いけそうだ！！！
1．正三角形を描く
2．1の正三角形の中に、1辺の長さが半分の正三角形を3つ描く。位置は上、左下、右下。
3．以下、再帰(2の正三角形の中に、半分の正三角形を描く）

できあがったもの

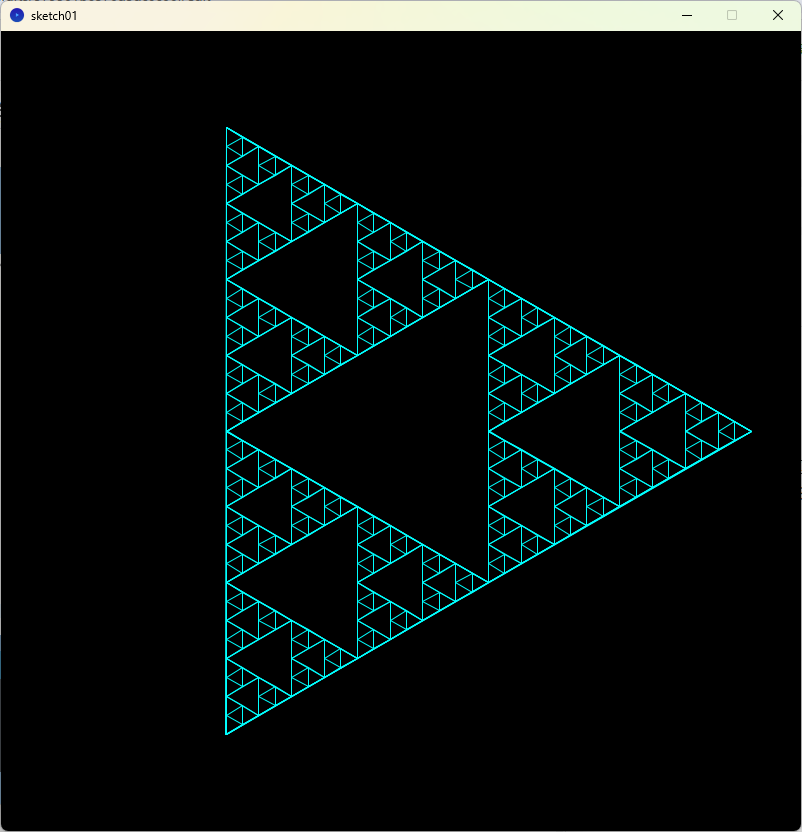
int maxCount = 5; // 再帰をやめる回数（これが無いと無限ループになる）
int pointNum = 3; // n角形を描く（今回は三角形）
 
void setup() {
  size(800, 800);
  background(0);
  stroke(0, 255, 255);
  
  // 初期サイズ
  float x = width / 2;
  float y = height / 2;
  float r = 350;
  
  fractal(r, x, y, 0);
}

// r = 1辺の長さ
// x = 中心のX座標
// y = 中心のX座標
// count = 再帰した回数
void fractal(float r, float x, float y, int count) {
  // 終了条件
  if (count > maxCount){
   return; 
  }
  
  // メイン処理（n角形を描く）
  float theta = PI * 2 / pointNum;

  // 頂点を決めて線を引く
  for(int i = 0; i < pointNum; i++ ){
   float x0 = x + r * cos( i * theta );
   float y0 = y + r * sin( i * theta );
   
   float x1 = x + r * cos( (i + 1) * theta );
   float y1 = y + r * sin( (i + 1) * theta );
   
   line(x0, y0, x1, y1);
  }
  
  // 自分自身を呼び出す
  for(int i = 0; i < pointNum; i++ ){
    float r2 = r / 2; // 1辺の長さが半分
    fractal( r2, x + r2 * cos(i * theta) , y + r2 * sin(i * theta), count + 1);
  }
}

失敗した

プログラムの中身が難しくなりすぎました

前半は超初心者向け記事でいい感じだったのに～。

敗因は三角関数(sin, cos)にあります。
三角形描くのに三角関数を使ったのですがコレ分かりにくいんですよね～。
でもこれが一番早い。
そしてProcessingで図形や動画を描くにあたって、三角関数は結構頻出だったりします。

子供に「三角関数なんていつ使うの？」と聞かれたら「プログラミングでお絵描きするとき」と答えましょう。

おまけ

ソース内のこの数字を変えて遊びました。

int maxCount = 5; // 再帰をやめる回数
int pointNum = 3; // n角形を描く

高井でした