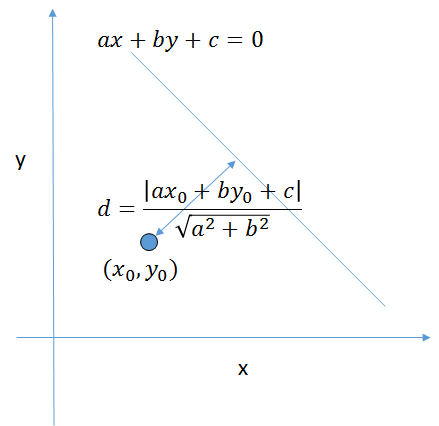1. サポートベクターマシン(Support Vector Machine:SVM)とは
前回の単純パーセプトロンからの機械学習入門では単純パーセプトロンの学習手法は、誤差関数の勾配を利用してどんどん誤差関数を小さくしていくというものだった。
だが、この手法には下記の2点の課題がある。
・モデルの汎化能力が保証されない。
・線形分離可能な問題で利用できない。
ここで、モデルとは学習が終わったあとの$f(x)$の式のことを指す。
また、汎化能力とは学習時に与えられた訓練データだけに対してだけでなく、未知の新たなデータに対するクラスラベルや関数値も正しく予測できる能力のことを指す。
そもそも、単純パーセプトロンのような機械学習を利用する目的は、スパムメールの例であれば、学習では使っていないメールでも上手くスパムかどうかを分類することである。
決して、以前にきたことのあるメールだけを分類すればいいというわけではない。
そんなものはシグネチャで十分に事足りることであり、機械学習の役割ではない。
話は逸れたが、SVMは上記の2点の課題を解決したアルゴリズムである。
この2点をどのように解決したのかというと、マージン最大化とカーネルトリックを導入したのである。
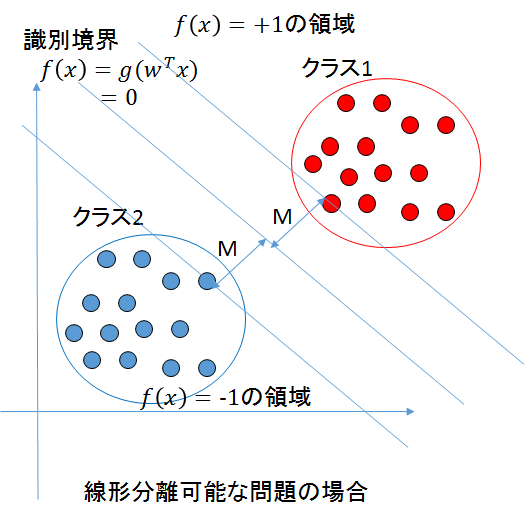
マージンとは、_f(x)_の線と2つのクラス間の距離のことを指す。
このマージン最大化とは、具体的には下記の図のMにあたる距離を最大化することで汎化能力を最大にしようという試みである。
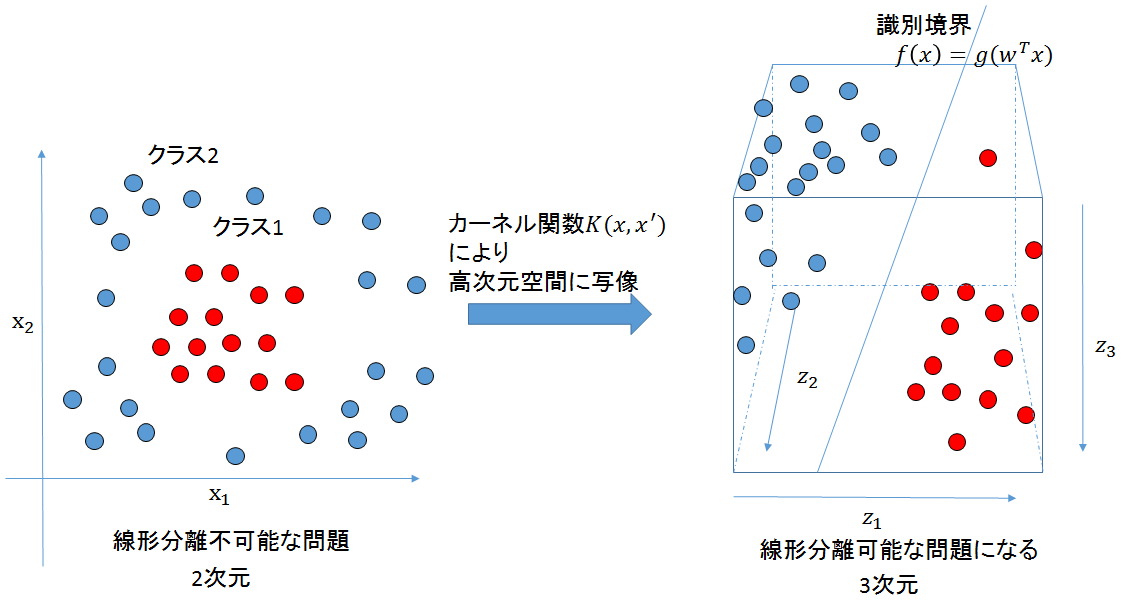
カーネルトリックとは、元々のデータ空間から高次元空間にデータを写像し、その高次元空間上で線形データ解析を行うことを指す。
小難しい話だが、カーネルトリックは下記の図のようなイメージのことをしていると考えればよい。
「なぜマージン最大化とカーネルトリックを利用することで2点の課題が解決されるのか」については後述する。
2. SVMの定式化
前回の単純パーセプトロンからの機械学習入門や今までで述べた内容では、データを学習する際にデータの中にノイズがあった場合どうするのかということまでは言及していなかった。
単純パーセプトロンの実装では、「誤差が0になるまで」学習を続けていた。
この場合、例えば、データが下記の図のようになっていた場合、前回の実装では永遠にパラメータを調整し続けることになるだろう。
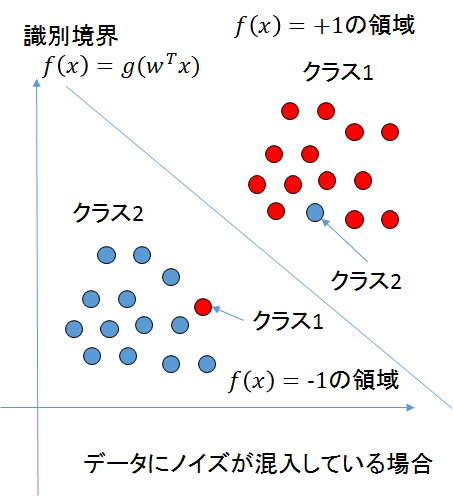
もちろん誤差が最小になったと判断した段階で学習をやめるような調整はできるが、その場合でも、ノイズの存在により分類の精度が下がってしまう。
SVMでもハードマージンSVMと呼ばれる実装では、データにノイズが混じっている場合に弱いという弱点がある。
そこで考えられたのが、データにノイズが混じっている場合にもある程度強いソフトマージンSVMである。
このソフトマージンSVMのようなノイズに強いモデルのことをロバストなモデルと呼ぶ。
現実の問題では、ノイズの含まれているデータが多く、ほとんどのタスクに対して、ソフトマージンSVMが用いられる。
ソフトマージンSVMよりも、ハードマージンSVMのほうがとっつきやすいので、今回はハードマージンSVMのみを解説する。
2.1. ヘッセの公式
高校の数Ⅱの教科書で見覚えのある方もいるかもしれないが、マージンを導出する際に用いられる公式であるヘッセの公式について説明する。
ここでは、公式の証明は行わず、どのように用いられるかのみ記述する。
ヘッセの公式とは、点と直線の距離を求めるための公式であり、下記の式により求められる。
点A(x_0,y_0) から、直線ax+by+c=0に下ろした垂線の長さdは、\\
d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}
SVMの導出では、これを多次元に拡張した下記を用いる。
データ点A=(x_1,x_2,...,x_m)から超平面f(x)=w^Tx+\thetaとの距離は \\
d=\frac{|w^Tx+\theta|} {||w||}
2.2. ラグランジュの未定乗数法
後述する制約条件のもとでマージンを最大化する際に、ラグランジュの未定乗数法を利用する。
ラグランジュの未定乗数法とは、ある条件のもとで問題を普通の極値問題として最適化を行う方法である。
2次元の場合の例を下記に示す。
制約条件$g(x,y)=0$のもとで、$f(x,y)$が最大値となる点$(a,b)$を求める問題
\left\{
\begin{array}{ll}
最大化 & f(x,y) \\
制約条件 & g(x,y)=0
\end{array}
\right.
を考える。\\
このとき、ラグランジュ乗数という未定の乗数$\lambda$を考えたとき、下記の関数を定義できる。
L(x,y,\lambda)=f(x,y)-\lambda g(x,y) \\
点(a,b)で\frac{\partial g}{\partial x}\neq0かつ\frac{\partial g}{\partial y}\neq 0のとき、\\
\frac{\partial L}{\partial x}=\frac{\partial L}{\partial y}=\frac{\partial L}{\partial \lambda}=0 \\
を満たす点$(x,y)$を、停留点として求めることで、最大値となる$(x,y)$が求まる。
また、ここで、停留点とは微分が0になるような点のことを指す。
これを一般の多次元に拡張した下記を用いてSVMを一般化する。
$M$個の制約条件$g_k(x_1,...,x_n)=0,(k=1,...,M)$のもとで、
$f(x_1,...,x_n)$が最大値となるn次元の点$x=(x_1,...,x_n)$を求める問題
\left\{
\begin{array}{ll}
最大化 & f(x_1,...,x_n) \\
制約条件 & g_k(x_1,...,x_n)=0,(k=1,...,M)
\end{array}
\right.
を考える。\\
このとき、ラグランジュ乗数という未定の乗数\lambda=(\lambda_1,...,\lambda_M)を考えたとき、下記の関数を定義できる。\\
L(x_1,...,x_n,\lambda)=f(x_1,...,x_n)-\sum_{k=1}^M\lambda_k g_k(x_1,...,x_n) \\
点(x_1,...,x_M)で\nabla g_k=(\frac{\partial f}{\partial x_1},...,\frac{\partial f}{\partial x_n})\neq (0,...,0)のとき、\\
N+M個の条件:\frac{\partial L}{\partial \alpha}=0(\alpha=x_1,...,x_n,\lambda_1,...,\lambda_M)\\
を満たす点(x_1,...,x_n)を停留点として求めることで最大値となる点(x_1,...,x_n)が求まる。
2.3. KKT(Karush-Kuhn-Tucker)条件
微分可能な関数$f,g_i$に対し、次のような不等式制約を持つ数理計画問題を考える。
\left\{
\begin{array}{ll}
最小化 & f(x) \\
制約条件 & g_i(x) \leq 0 (i=1,...,m)
\end{array}
\right.
下記の式が上記に対するKKT条件である。
\left\{
\begin{array}{l}
\nabla f(\hat{x})+\sum_{i=1}^m \hat{\lambda_i} \nabla g_i(\hat{x})=0 \\
\hat{\lambda_i} \geq 0,g_i(\hat{x})\leq 0,\hat{\lambda_i} g_i(\hat{x}) = 0 (i=1,...,m)
\end{array}
\right.
ここで上記の式で
\hat{\lambda_i} \geq 0,g_i(\hat{x})\leq 0,\hat{\lambda_i} g_i(\hat{x}) = 0 (i=1,...,m)
は、各$i$について、$\hat{\lambda_i},g_i(\hat{x})$の少なくとも一方が0となることを表しており、一般に相補性条件と呼ばれている。
2.4. ハードマージンSVMの導出
学習データの総数がn個のとき、学習データと超平面の最小距離dは、『2.1. ヘッセの公式』により、下記で与えられる。
d=min_{i=1,...,n}\{\frac{|w^Tx_i+\theta|}{||w||}\} \\
ここで、$min_{i=1,...,n}$とは$i$が$1~n$の中で関数内の計算結果が最も小さい値をとるときの値を返す関数である。
この最小距離$d$を最大化する$w$と$\theta$を求めたい。これを式にすると、下記になる。
d_{max}=max_{w,\theta}[min_{i=1,...,n}\{\frac{|w^Tx_i+\theta|}{||w||}\}]
ここで、$max_{w,\theta}$とは取り得る$w$と$\theta$の中で関数内の計算結果が最も大きい値を返す関数である。
このとき、$||w||$は$i$に結果が依存しないので、$min$関数の外に出すことができることから
d_{max}=max_{w,\theta}[\frac{1}{||w||}min_{i=1,...,n}\{|w^Tx_i+\theta|\}] \\
と表せる。
$w^Tx+\theta=0$のとき、$\frac{1}{||w||}$がどのような値をとろうと、
$d_max$は0になり、$w,\theta$が一意に決まらないことから、下記の制約を付加する。
min_{i=1,2,...,n}|w^Tx_i+\theta|=1
これにより、
max_{w,\theta}\frac{1}{||w||} \\
となる識別関数を求めればよい。\\
超平面から両側の学習データまでM=\frac{1}{||w||}離れており、
\frac{2}{||w||}の幅(マージン:margin)を持つ。\\
max_{w,\theta}\frac{1}{||w||}は計算的側面からmin_{w,\theta}\frac{1}{2}||w||^2と同等になる。 \\
また、教師ラベルt_iを用いることで、制約条件min_{i=1,2,...,n}|w^Tx_i+\theta|=1は下記のように書ける。 \\
t_i(w^Tx_i+\theta)\geq 1,(i=1,2,...,n) \\
教師データ$t_i$と識別関数$w^Tx_i+\theta$の演算結果が食い違っていた場合、$t_i(w^Tx_i+\theta)<1$となる。
つまり、上記の制約条件を満たしていることは、誤識別が発生していないことを示す。
誤識別が発生していない条件の下で$\frac{1}{2}||w||^2$を最小化する問題に帰着することができる。
これを定式化すると、下記のようになる。
\left\{
\begin{array}{l}
min_{w,\theta}\frac{1}{2}||w||^2 \\
制約条件 :t_i(w^Tx_i+\theta)\geq 1,(i=1,2,...,n)
\end{array}
\right.
このとき、ラグランジュ乗数という未定の乗数$\lambda(\lambda_i\geq 0)$を考えたとき、下記の関数を定義できる。
この関数の最小値を求めるという問題に置き換えることができる。
L(w,\theta,\lambda)=\frac{1}{2}||w||^2-\sum_{i=1}^{N}\lambda_i{t_i(w^Tx_i+\theta)-1} \\
最小値では、Lの傾き(勾配)が0になるはずなので\\
\frac{\partial L}{\partial b}=\sum_{i=1}^{N}\lambda_it_i=0 \\
\frac{\partial L}{\partial w}=w-\sum_{i=1}^{N}\lambda_i t_i x_i=0 \\
\frac{\partial L}{\partial w}の右辺を変形すると、下記のようになる。 \\
w=\sum_{i=1}^{N}\lambda_i t_i x_i \\
L(w,\theta,\lambda)を計算しやすいように展開する。\\
L(w,\theta,\lambda)=\frac{1}{2}||w||^2-\sum_{i=1}^{N}\lambda_it_iw^Tx_i+\lambda_it_i\theta-\lambda_i \\
L(w,\theta,\lambda)=\frac{1}{2}||w||^2-\sum_{i=1}^{N}\lambda_it_iw^Tx_i-\theta\sum_{i=1}^{N}\lambda_it_i+\sum_{i=1}^{N}\lambda_i \\
ここで\thetaが\sum_{i=1}^{N}の外に出ているのは、定数だからである。\\
L(w,\theta,\lambda)に\sum_{i=1}^{N}\lambda_it_i=0,w=\sum_{i=1}^{N}\lambda_i t_i x_iを代入する。 \\
L(w,\theta,\lambda)=\frac{1}{2}||w||^2-\sum_{i=1}^{N}\lambda_it_ix_i\sum_{j=1}^{N}\lambda_j t_j x_j-\theta×0+\sum_{i=1}^{N}\lambda_i \\
L(w,\theta,\lambda)=\frac{1}{2}w\cdot w-\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i \\
L(w,\theta,\lambda)=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i \\
L(w,\theta,\lambda)=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i \\
これを双対形式として、下記のように整理できる。\\
\left\{
\begin{array}{l}
max_{\lambda}-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i \\
制約条件 :\sum_{i=1}^{N}\lambda_it_i=0,\lambda_i\geq 0
\end{array}
\right. \\
このような問題を$\lambda_i$に関する凸2次計画問題と呼ぶ。
この式の解$\hat{\lambda_i}(>0)$が求まると、$w=\sum_{i=1}^{N}\lambda_i t_i x_i$から$\hat{w}$が得られる。
この凸2次計画により、局所的最適解は必ず大局的最適解になる。
最適解 $\hat{w},\hat{\theta},\hat{\lambda}$はKKT相補条件$\hat{\lambda_i}t_i(w^Tx_i+\theta)-1=0$を満たさなければならない。
不等式制約条件$ t_i(w^Tx_i+\theta)-1>0 $を満たすとき、相補条件から$\lambda_i = 0$でなければならない。
そのため、この制約は有効でなくなる。
また、$t_i(w^Tx_i+\theta)-1=0$の場合は$\lambda_i>0$となれるので、制約が有効になる。
このことから、$t_i(w^Tx_i+\theta)-1=0$を満たすマージンを決める点(以下、サポートベクター)による制約のみを有効化している。
サポートベクターは元のサンプル数に比べて、かなり数が少ないので、識別を行う際には計算量の大きな節約となる。
最終的にSVMは下記のように導出される。
f(x)=w^Tx+\theta,w=\sum_{i=1}^{N}\lambda_i t_i x_iより、\\
\hat{f}(x)=\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j +\theta
$\theta$の値は相補性条件$t_i(w^Tx_i+\theta)-1=0$より下記のように求められる。
t_i(w^Tx_i+\theta)-1=0,w=\sum_{i=1}^{N}\lambda_i t_i x_iより、\\
t_i(\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j+\theta)-1=0 \\
両辺をt_iで割ると\\
\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j+\theta - \frac{1}{t_i}=0\\
\theta以外の項を移項して \\
\theta=\frac{1}{t_i} -\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j\\
\frac{1}{t_i}はt_i\in \{1,-1\}であることからt_iと等価と言えるため、\\
\theta=t_i -\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j
$\theta$を実際の実装で求める際、数値計算上の安定性を考慮し、条件を満たす全てのサポートベクターを用いて平均をとることが多い。
平均をとる場合、$\theta$は下記の式により求められる。
\theta = \frac{1}{N_S} \sum_{n \in S}(t_n - \sum_{m \in S}\hat{\lambda}_mt_m x_n^T x_m) \\
S:サポートベクターの集合(=\{s_1,s_2,...,s_{N_S}\}) \\
N_S:サポートベクターの数
最終的には下記のような式で識別境界を描画する。
\hat{f}(x)=\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j + \frac{1}{N_S} \sum_{n \in S}(t_n - \sum_{m \in S}\hat{\lambda}_mt_m x_n^T x_m)
3. カーネルトリック
マージンを最適化したことにより、単純パーセプトロンと比較すると汎化能力の向上が期待できるようになった。
しかし、ここまでの実装では線形分離可能問題以外を解くことができないことは変わらない。
この課題を解決するために考えられたのが、カーネルトリックである。
カーネルトリックがやっていることは冒頭でも説明したかと思うが、「元々のデータ空間から高次元空間にデータを写像し、その高次元空間上で線形データ解析を行うこと」である。
ここではどうやって実装するかについてのみ述べ、なぜそうなるのかなど実装自体には影響はないことに関しては高度すぎるので省く。
先ほど最終的に求まった下記の式を変形する。
\hat{f}(x)=\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j + \frac{1}{N_S} \sum_{n \in S}(t_n - \sum_{m\in S}\hat{\lambda}_mt_m x_n^T x_m)
これをこうする。
\hat{f}(x)=\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i K(x_i,x_j) + \frac{1}{N_S} \sum_{n \in S}(t_n - \sum_{m \in S}\hat{\lambda}_mt_m K(x_n,x_m)
$K(\cdot,\cdot)$はカーネル関数である。
カーネルトリックについて詳しく知りたい場合は、カーネル法を学ぶといい。
具体的には再生核ヒルベルト空間やRepresenter定理、Mercerの定理などを学習する必要がある。
4. SVMの学習アルゴリズム
$\lambda$を最適化する手法で代表的なものは下記の3つある。
4.1. 最急降下法による学習
最急降下法とは、関数の傾きから関数の最小値を探索するアルゴリズムである。
$n$ 次のベクトル $x = (x1, x2, ... , xn)$ を引数とする関数を $f (x)$ としてこの関数の極小値を求めることを考える。
勾配法では反復法を用いて $x$ を解に近づけていく。$k$ 回目の反復で解が $x^(k)$ の位置にあるとき、最急降下法では下記のようにして値を更新する。
関数を最小化するとき
x^{(k+1)} = x^{(k)}-\alpha \nabla f(x^{(k)})
関数を最大化するとき
x^{(k+1)} = x^{(k)}+\alpha \nabla f(x^{(k)})
学習は坂道を転がり落ちるように更新が行われていく下記の図のような動きをする。
図では視覚化のため、1次元だが、多次元の場合についても同じである。
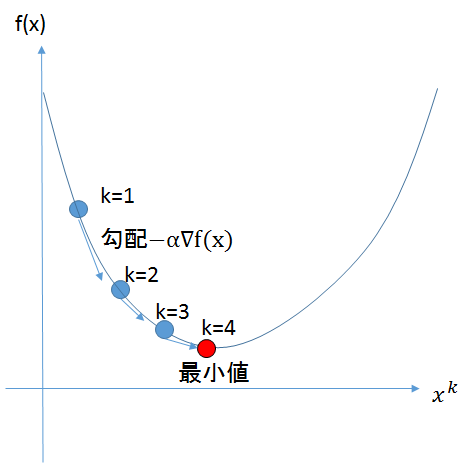
$\alpha$の値は任意の数値を使う。(一般的には0~1の間の数値)
$\alpha$が大きすぎると、一度の更新で坂を降りる距離が大きくなり、小回りがきかなくなるため、実際の最小値と算出された近似値とのギャップが大きくなる。
$\alpha$が小さすぎると、一度の更新で坂を降りる距離が小さくなるため、計算量が大幅に増加する。
そのため、$\alpha$の値を適切に設定することも、機械学習エンジニアの腕の見せ所である。
今回は一番実装が簡単な最急降下法を実装する。
最急降下法のSVMへの定式化を下記に示す。
$L(w,\theta,\lambda)$を最大化する変数$\lambda$を考える。
\lambda_i^{(k+1)}=\lambda_i^{(k)}+\alpha \nabla L(w,\theta,\lambda) \\
\lambda_i^{(k+1)}=\lambda_i^{(k)}+\alpha \frac{\partial L(w,\theta,\lambda)}{\partial \lambda} \\
L(w,\theta,\lambda)=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_iより、 \\
\lambda_i^{(k+1)}=\lambda_i^{(k)}+\alpha (1-\sum_{j=1}^{N} \lambda_j t_i t_j x_i^T x_j) \\
\lambda_i^{(k+1)}=\lambda_i^{(k)}+\alpha (1-\sum_{j=1}^{N} \lambda_j t_i t_j K(x_i,x_j))
上記の式により、変数$\lambda$を更新していく。
4.2. SMOアルゴリズムによる学習
SMOアルゴリズムとは、最適化する対象の2変数を選び取り、反復的に更新を行っていく最適化手法である。
世界的に有名なSVMのライブラリである、LIBSVMでも採用されている。
実装自体は下記のページにC++のものならある。
http://web.cs.iastate.edu/~honavar/smo-svm.pdf
http://www.cs.mcgill.ca/~hv/publications/99.04.McGill.thesis.gmak.pdf
ここではこれ以上触れないが、そのうち、解説記事とともに公開するつもりではある。
4.3. 確率的勾配降下法による学習
確率的勾配降下法(SGD)とは、平たく言えば、バッチ学習である最急降下法をオンライン学習に改良した物である。
やや最近の論文では、下記のPegosasという実装が提案されている。
http://ttic.uchicago.edu/%7Enati/Publications/PegasosMPB.pdf
確率的勾配降下法を用いることにより、SVMでオンライン学習を行うことができるらしい。
ここではアルゴリズムの詳細については知らないため、省略する。
そのうち実装してみたい。
5. pythonによるハードマージンSVM実装例
一応できたにはできたっぽいが、サポートベクトルが算出されなかったり、変なサポートベクトルが算出される場合がある。
おそらく、原因は最急降下法の実装部分で、どこか間違えているか更新回数を決めている点だと考えられる。
ラグランジュ乗数の値が収束していればサポートベクトルをきちんと発見できそうな気もしなくもない。
原因が分かる人は教えていただきたい。
SVMを一度大学生のときに実装したときにはこんな変な躓き方はしていないので、わりと謎だ。(当時のソースコードは紛失した)
最急降下法の更新式でオーバーフローしたときにサポートベクトルが算出されていないので、
やる気が出ればそのうち値に上限を定めようかと思う。
# -*- coding: utf-8 -*-
# ファイル名はsvm.py
import numpy as np
import random
from math import fabs
from scipy.linalg import norm
import matplotlib.pyplot as plt
# SVMのクラス
class svm:
#初期値の設定
def __init__(self,kernel='linear',sigma=1.,degree=1.,threshold=1e-5,loop=500,LR=0.2):
self.kernel = kernel
# 線形カーネルのときは多項式カーネルのパラメータを全て1にしたときと等価
if self.kernel == 'linear':
self.kernel = 'poly'
self.degree = 1.
# RBFやPoly(多項式)カーネルの場合のパラメータ
self.sigma = sigma
self.degree = degree
# サポートベクトルを見つける際のしきい値
self.threshold = threshold
# 更新回数
self.loop = loop
# 学習率
self.LR = LR
# カーネルの計算を行うメソッド
def build_kernel(self,X):
self.K = np.dot(X,X.T)
if self.kernel == 'poly':
self.K = (1. + 1. / self.sigma * self.K)**self.degree
if self.kernel == 'rbf':
self.xsquared = (np.diag(self.K)*np.ones((1,self.N))).T
b = np.ones((self.N,1))
self.K -= 0.5*(np.dot(self.xsquared,b.T) + np.dot(b,self.xsquared.T))
self.K = np.exp(self.K/(2.*self.sigma**2))
# SVMの学習部分のメソッド
def train_svm(self,X,t):
# 最急降下法開始
# self.NにXの行数を代入
self.N = np.shape(X)[0]
# kernelを計算
self.build_kernel(X)
count = 0
# ラグランジュ乗数の初期化
lam = np.ones((self.N,1))
# 指定した更新回数分ループする
while(count < self.loop):
for i in range(self.N):
ans = 0
for j in range(self.N):
# 最急降下法の更新式の一部
ans += lam[j]*t[i]*t[j]*self.K[i,j]
# 最急降下法の更新式
lam[i] += self.LR * (1-ans)
# ラグランジュ乗数は0以上なので負の値をとると、0を代入する。
if lam[i] < 0:
lam[i] = 0
count += 1
# 最急降下法終了
# しきい値以上の値となったラグランジュ乗数をサポートベクトルとして取り出す
self.sv = np.where(lam>self.threshold)[0]
# サポートベクトルの数
self.nsupport = len(self.sv)
print self.nsupport,"support vector found"
# それぞれサポートベクトルのデータのみを格納していく
self.X = X[self.sv,:]
self.lam = lam[self.sv]
self.t = t[self.sv]
# wの計算式
self.w = np.array([0.,0.])
for i in range(self.nsupport):
self.w += self.lam[i]*self.t[i]*self.X[i]
# θの計算式
self.b = np.sum(self.t)
for n in range(self.nsupport):
self.b -= np.sum(self.lam*self.t*np.reshape(self.K[self.sv[n],self.sv],(self.nsupport,1)))
self.b /= len(self.lam)
# 線形カーネルか多項式カーネルの場合の分類部分
if self.kernel == 'poly':
def classifier(Y):
K = (1. + 1./self.sigma*np.dot(Y,self.X.T))**self.degree
self.y = np.zeros((np.shape(Y)[0],1))
for j in range(np.shape(Y)[0]):
for i in range(self.nsupport):
self.y[j] += self.lam[i]*self.t[i]*K[j,i]
return self.y
# RBFカーネルの場合の分類部分
elif self.kernel == 'rbf':
def classifier(Y):
K = np.dot(Y,self.X.T)
c = (1./self.sigma * np.sum(Y**2,axis=1)*np.ones((1,np.shape(Y)[0]))).T
c = np.dot(c,np.ones((1,np.shape(K)[1])))
aa = np.dot(self.xsquared[self.sv],np.ones((1,np.shape(K)[0]))).T
K = K - 0.5*c - 0.5*aa
K = np.exp(K/(2.*self.sigma**2))
self.y = np.zeros((np.shape(Y)[0],1))
for j in range(np.shape(Y)[0]):
for i in range(self.nsupport):
self.y[j] += self.lam[i]*self.t[i]*K[j,i]
self.y[j] += self.b
return self.y
else:
print "[Error] There is not this Kernel --",self.kernel
return
self.classifier = classifier
if __name__ == "__main__":
from svm import svm
# 訓練データを定義
cls1 = [] #クラス1
cls2 = [] #クラス2
mean1 = [-1, 2]
mean2 = [1, -1]
cov = [[1.0,0.8], [0.8, 1.0]]
N = 100
#乱数により、クラス1の訓練データを作成
cls1.extend(np.random.multivariate_normal(mean1, cov, N/2))
#乱数により、クラス2の訓練データを作成
cls2.extend(np.random.multivariate_normal(mean2, cov, N/2))
# データ行列Xを作成
X = np.vstack((cls1, cls2))
# ラベルtを作成
t = []
for i in range(N/2):
t.append(1.0) # クラス1
for i in range(N/2):
t.append(-1.0) # クラス2
t = np.array(t)
# 訓練データを描画
x1, x2 = np.array(cls1).transpose()
plt.plot(x1, x2, 'rx')
x1, x2 = np.array(cls2).transpose()
plt.plot(x1, x2, 'bx')
sv = svm(kernel='linear',degree=3)
# svmを学習
sv.train_svm(X,t)
# サポートベクトルを描画
for n in sv.sv:
plt.scatter(X[n,0], X[n,1], s=80, c='c', marker='o')
# 識別境界を描画
step = 0.1
f0,f1 = np.meshgrid(np.arange(np.min(X[:,0])-0.5, np.max(X[:,0])+0.5, step), np.arange(np.min(X[:,1])-0.5, np.max(X[:,1])+0.5, step))
out = sv.classifier(np.c_[np.ravel(f0),np.ravel(f1)]).T
out = out.reshape(f0.shape)
plt.contour(f0,f1,out,1)
plt.show()
6. 参考文献
6.1. ヘッセの公式
2次元のとき
http://www004.upp.so-net.ne.jp/s_honma/urawaza/distance.htm
3次元のとき
http://yosshy.sansu.org/distance1.htm
6.2. ラグランジュの未定乗数法
http://fd.kuaero.kyoto-u.ac.jp/sites/default/files/Lagrange1.pdf
https://ja.wikipedia.org/wiki/%E3%83%A9%E3%82%B0%E3%83%A9%E3%83%B3%E3%82%B8%E3%83%A5%E3%81%AE%E6%9C%AA%E5%AE%9A%E4%B9%97%E6%95%B0%E6%B3%95
6.3. KKT条件
6.4. SVM
Machine Learning: An Algorithmic Perspective, Second Edition (Chapman & Hall/Crc Machine Learning & Pattern Recognition)
Rで学ぶデータサイエンス6 マシンラーニング
辻谷 将明 (著), 竹澤 邦夫 (著), 金 明哲 (編集)
サポートベクトルマシン
竹内 一郎 (著), 烏山 昌幸 (著)
はじめてのパターン認識
平井 有三 (著)
Pegasos: Primal Estimated sub-GrAdient SOlver for SVM
Shai Shalev-Shwartz,Yoram Singer,Nathan Srebro