単純パーセプトロンからの機械学習入門

#1.単純パーセプトロンとは
下記の線形識別関数を用いて、入力されたデータを２クラスに分類する。

f(x)=g(w^{T}x+\theta)\\
ここで、\theta = x_0とおくと、  \\
    =g(\sum _{i=0}^{d}w_ix_i)

非線形活性化関数：g(a) = \left\{
\begin{array}{ll}
+1 & (a \geq 0) \\
-1 & (a \lt 0)
\end{array}
\right.

重み：w=(w_0,w_1,...,w_{d})、　\\
入力データ：x=(x_0=\theta,x_1,x_2,...,x_{d})、
\\d：次元数、

バイアス：\theta(任意の数値)

f(x) \geq 0 のとき、x\in C_{1}

f(x) \lt 0 のとき、x\in C_{2}

C_1:クラス1、C_2:クラス2

上記のうち、重み_w_のパラメータを決めるための処理は「学習」と呼ばれる。
バイアス_θ_(バイアスパラメータ)はデフォルトでも使えなくはないが、より良い結果になるように人の手で調整(チューニング)する。
このバイアスのような人の手で調整するものは一般的にパラメータ(ハイパーパラメータとかチューニングパラメータ)と呼ばれ、パラメータを調整することをパラメータチューニングと呼ぶこともある。

～パラメータの用例～
　「単純パーセプトロンでパラメータチューニングしたらそれなりの結果出たンゴ」

また、チューニング方法は様々存在し、人が手動でひたすら試す方法やグリッドサーチ、ランダムサンプリングなどがある。

##1.1.どんなことに使える？
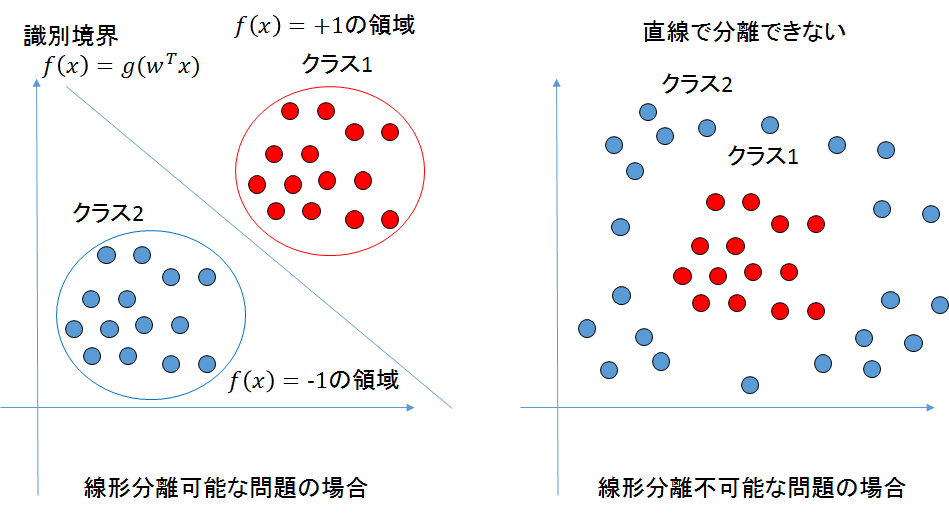
２クラス問題で線形分離可能な問題で使える。
線形分離可能な問題とは、大まかに言ってしまえば、2次元の場合はクラス1の集合とクラス2の集合を1本の直線で分離できる問題のことを指す。
これを一般化して、n_次元空間上のクラス1の集合とクラス2の集合を_n-1次元の超平面で分離できることも線形分離可能と呼ぶ。
線形分離可能な場合と線形分離不可能な場合の例を図にしたものを下記に示す。

パーセプトロンのような教師あり学習のアルゴリズムの具体的な応用例としてよくあげられるのが、スパムメールの判定である。
大まかには下記の手順により、スパムメールの判定は行われる。
　1.スパムメールと通常のメールの２クラスを仮定する。
　2.次に両方のメールから特徴ベクトル(or特徴量or素性)と教師ラベル(スパムか正常かのラベル)を作成する。
　　※余談だが、自然言語処理の分野では素性という呼び方がよく使われる。
　3.特徴ベクトルと教師ラベルを学習器(今回は単純パーセプトロン)に入力し、学習を行う。
　4.出来上がった数理モデル(今回は線形識別関数モデル)を用いて、判定を行う。

特徴ベクトルは、定性的なデータからデータの特徴をうまく残して定量化したものである必要がある。
これによって、精度が大きく変わる場合があり、非常に重要な作業である。
特徴ベクトルの作成手法の具体例を下記にあげる。

【例：特徴ベクトル作成手法】
　　下記のようなデータがあったとして、件名でスパムかどうかを判別したい。

　　　　・スパムメールの件名：彼氏がオオアリクイと戦って死んでしまいました
　　　　・通常のメールの件名：打ち合わせ時間変更の依頼

　　自然言語処理の分野で良く使われる技術に、形態素解析という技術がある。
　　形態素解析を行うツールとしては、MeCabやCabochaなどが有名である。
　　形態素解析により、入力した文章を形態素(言語で意味を持つ最小単位)に分けることができる。
　　これにより、以下のような文ができあがる。(国語苦手な人間による形態素解析なので精度は保証しない)

　　　　・スパムメールの件名：彼氏/が/オオアリクイ/と/戦って/死んで/しまいました/
　　　　・通常のメールの件名：打ち合わせ/時間/変更/の/依頼/

　　次に上記のデータを使って形態素の辞書を作成する。
　　その結果、辞書は下記のようになる。

    辞書 \in\{彼氏,が,オオアリクイ,と,戦って,死んで,しまいました,打ち合わせ,時間,変更,の,依頼\}

　　※上記は自然言語処理の分野では誰かが作った辞書のデータを使ったり、手作業で入力して作成するので、一般的な方法ではない。
　　この辞書を作成する際に、全ての形態素を動詞なら基本形に直して辞書に入れるなどの工夫を行い、精度をあげていく。

　　最後に先ほど作成した辞書を用いて、特徴ベクトルを作成すると下記のようになる。

スパムメールの特徴ベクトルx_1=\{1,1,1,1,1,1,1,0,0,0,0,0\},教師ラベルt=\{-1\}

通常のメールの特徴ベクトルx_2=\{0,0,0,0,0,0,0,1,1,1,1,1 \},教師ラベルt=\{+1\}

　　どのように特徴ベクトルを作成しているのかというと、辞書に含まれている単語の出現の有無(1:有、0:無)を配列に格納している。
　　この方法はBag-Of-Words法(単語袋詰め法)と呼ばれる。
　　単語の出現の有無ではなく、単語の出現回数で作成する場合もある。
　　また、この拡張として、Tf-idfという重み付け手法も存在する。
　　これは、多くの文書に出現する語の重要度を下げ、特定の文書にしか出現しない単語の重要度を上げる目的で利用される。
　　さらっと、教師ラベルを決めているが、一般的には確率モデルで利用される場合は0と1、パーセプトロンのような活性化関数と相性のいい-1と1が適用されることが多い。

以上が特徴ベクトルの作成手順である。

また、線形分離可能な問題で使えるという根拠は「パーセプトロンの収束定理」により説明できる。
証明は下記を参照されたし。
http://ocw.nagoya-u.jp/files/253/haifu%2804-4%29.pdf

#2.パーセプトロンの学習(確率的最急降下アルゴリズム)
学習方法のコンセプトは簡単で、間違えたら_w_の値を後述の式により更新していき、間違いがなくなるまで更新を続ける。
学習データの系列を下記のように定義する。

X=\{X_1,X_2,...,X_M\} \\
M:データ数

ここで、誤分類された学習データの集合を下記のように表記する。

X_n=\{x_1,x_2,...,x_n\}

クラス1のデータに対し、f(x) > 0,クラス2のデータに対し、f(x) < 0となるような重み_w_を求めたい。
この場合、教師ラベル_t_={+1,-1}を用いると、全てのデータは下記を満たす。

w^Tx_it_i>0

正しく分類されたデータに対し、誤差0を割り当てるような下記の誤差関数E(・)が考えられる。

E(w) =-\sum_{n \in X} w^Tx_nt_n

これを最小化する(0になる)ように、_w_の値を設定すれば、上手く分類できる。
この最小化する手法として、確率的勾配降下法を利用する。
確率的勾配降下法は誤差関数が今回の_E(w)_のようにデータ点の和からなっている場合、データ_n_が与えられたとき、下記の計算によりwを更新する。

w^{(r+1)}=w^{(r)}-\mu \nabla E_n \\
r：繰り返しの回数、\mu：学習率パラメータ \\
w^{(r)}:r回更新した後の重みw

上記から、下記のように更新式が導出できる。

w^{(r+1)}=w^{(r)}-\mu \nabla E(w) \\
=w^{(r)}+\mu x_nt_n 

_w_の値次第で、データが誤分類されてしまうような領域内では、_t_の値が+1のときでも-1のときでも、誤分類されたデータの誤差_E(w)_への寄与は線形関数となる。
また、_w_の値次第で、データが正しく分類される領域内ではデータの誤差_E(w)_への寄与は0である。
したがって、_E(w)_は区分線形関数である。
そのため、_E(w)_の勾配は下記のように計算されている。

E(w) = \frac{\partial E(w)}{\partial w} \\
=x_nt_n 

#3.Pythonによる実装
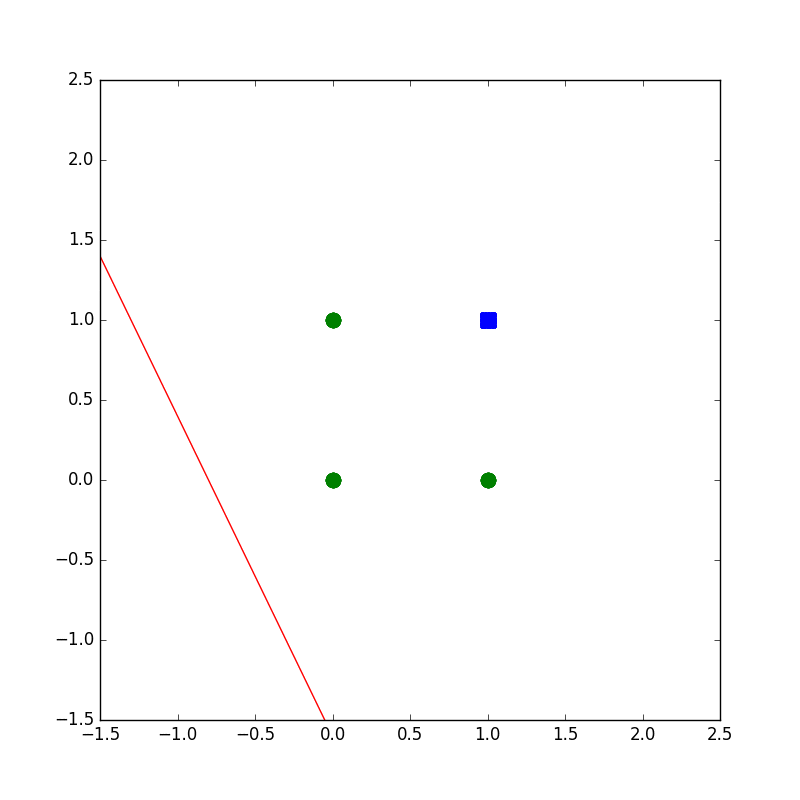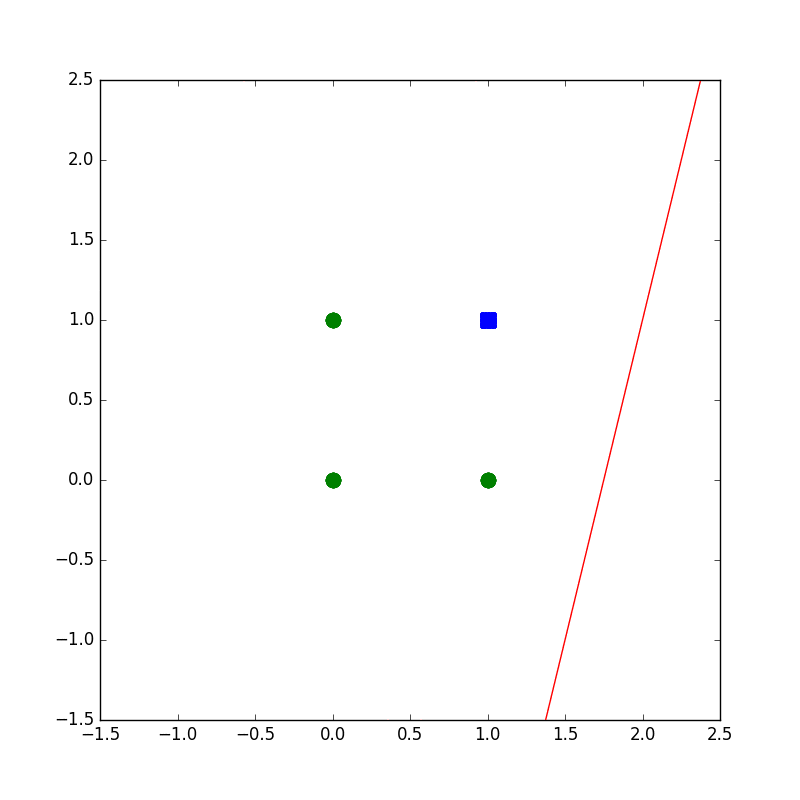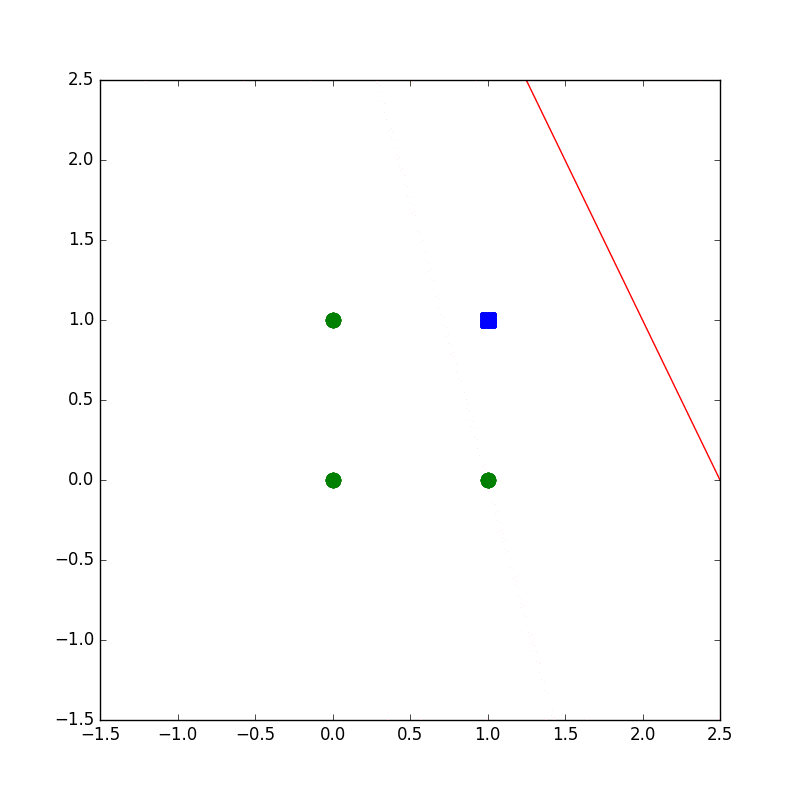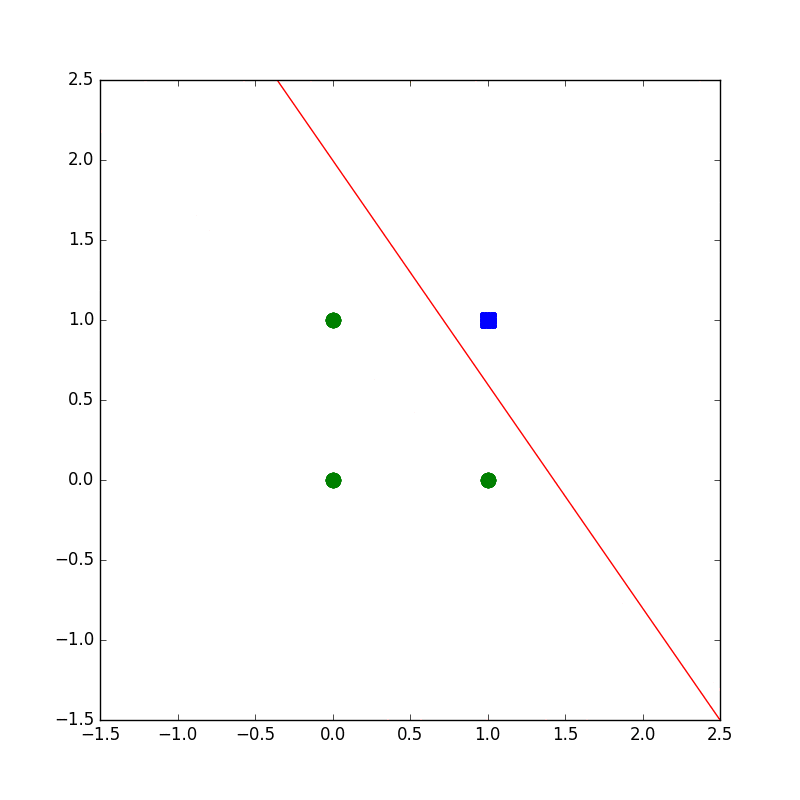
下記のコードは設計もへったくれもないAND演算がパーセプトロンで解ければいいやというコードです。
学習の様子がプロットされるようになってます。
本来ならクラスかメソッドにしろよという感じかもしれませんが、ご了承ください。
気が向いたら書き直します。
実行には、_numpy_と_matplotlib_のライブラリのインストールが必要です。

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# 非活性化関数g(x)のメソッド
def predict(w,x):
  out = np.dot(w,x)
  if out >= 0:
    o = 1.0
  else:
    o = -1.0
  return o

# プロットするメソッド
def plot(wvec,x1,x2):
  x_fig=np.arange(-2,5,0.1)
  fig = plt.figure(figsize=(8, 8),dpi=100)
  ims = []
  plt.xlim(-1,2.5)
  plt.ylim(-1,2.5)
  # プロットする
  for w in wvec:
    y_fig = [-(w[0] / w[1]) * xi - (w[2] / w[1]) for xi in x_fig]
    plt.scatter(x1[:,0],x1[:,1],marker='o',color='g',s=100)
    plt.scatter(x2[:,0],x2[:,1],marker='s',color='b',s=100)
    ims.append(plt.plot(x_fig,y_fig,"r"))
  for i in range(10):
    ims.append(plt.plot(x_fig,y_fig,"r"))
  ani = animation.ArtistAnimation(fig, ims, interval=1000)
  plt.show()

if __name__=='__main__':
  wvec=[np.array([1.0,0.5,0.8])]# 重みベクトルの初期値、適当
  mu = 0.3 # 学習係数
  sita = 1 # バイアス成分

  # AND関数のデータ(一番後ろの列はバイアス成分:1)
  x1=np.array([[0,0],[0,1],[1,0]]) #クラス1(演算結果が0)の行列生成
  x2=np.array([[1,1]]) # クラス2(演算結果が1)の行列生成
  bias = np.array([sita for i in range(len(x1))])
  x1 = np.c_[x1,bias] #バイアスをクラス1のデータ最後尾に連結
  bias = np.array([sita for i in range(len(x2))])
  x2 = np.c_[x2,bias] #バイアスをクラス2のデータ最後尾に連結
  class_x = np.r_[x1,x2] # 行列の連結

  t = [-1,-1,-1,1] # AND関数のラベル
  # o:出力を求める
  o=[]
  while t != o:
    o = [] # 初期化
    # 学習フェーズ
    for i in range(class_x.shape[0]):
      out = predict(wvec[-1], class_x[i,:])
      o.append(out)
      if t[i]*out<0: #出力と教師ラベルが異なるとき
        wvectmp = mu*class_x[i,:]*t[i] #wを変化させる量
        wvec.append(wvec[-1] + wvectmp) #重みの更新
  plot(wvec,x1,x2)

#4.単純パーセプトロンを拡張した代表的なアルゴリズム
・SVM
・多層パーセプトロン

#5.参考文献
パターン認識と機械学習 上

はじめてのパターン認識